柔性绳系辅助离轨系统展开动力学研究
曹喜滨,郑鹏飞,张世杰
(哈尔滨工业大学卫星研究所,150001哈尔滨,pfzheng.hit@163.com)
为了更好的分析柔性系绳展开运动特性,在基本假设的前提下采用进一步的假设:
1)绳系辅助离轨系统没有摆动运动或可控—相对某一平衡位置作微幅的振荡(以静态释放模式为例,即θ=φ=θ·=˙φ=ε,L·/L=D,D和ε为小量);
2)C1≫Ci,i=2,3,…,n;
3)与返回舱质量相比,系绳质量可以忽略,不考虑外界摄动作用.
基于上述假设,采用二阶伽辽金模型,由式(7),(8)和(10)可得展开状态下的柔性绳系辅助离轨系统的横、纵向运动的系数方程为
结合俄罗斯提出的充气式防热罩技术[1]和绳系辅助离轨技术的绳系辅助返回系统[2-3],将是未来空间站有效载荷返回的一种有效手段.与传统的空间返回系统相比,绳系辅助返回系统具有发射成本低、效率高、可部分重复使用的特点.而在该系统中,绳系辅助离轨系统的离轨效率直接决定了返回舱再入点的位置和精度,从而影响了返回舱的再入状态以及落点精度,即直接影响或决定了绳系辅助返回任务的成败.
自从上世纪60年代苏联科学家尤里阿特苏塔诺夫提出的‘太空梯’概念以来,国内外学者提出了基于绳系系统的多项应用技术和概念,如绳系辅助编队飞行、绳系卫星技术、无动力或电动力缆绳辅助离轨技术等;并对理想情况下的绳系系统展开、系留以及回收的动力学和控制进行了大量的研究[4-8];然而由于绳系辅助离轨系统任务的特殊性—需要保证返回舱再入点精度,对绳系辅助离轨系统的展开控制提出了更高要求,因而研究复杂情况下的绳系辅助离轨系统的展开动力学及控制已经成为必要.
国内外学者对复杂绳系系统的动力学问题也进行了大量的研究,如 Lanoix等[9-10]针对不同的空间任务,研究了空间摄动下绳系系统系留状态的稳定性及任务寿命等问题,并建立了系留状态下的刚性和柔性的绳系系统模型;No等[11]基于“珠子模型”建立了柔性有质量分布系绳的系留运动的运动学和动力学模型,Banerjee等[12]在此基础上,通过改变珠子的质量和连接杆的长度,研究了柔性有质量分布系绳的展开以及回收运动的动力学建模问题;刘良栋等[13]在绳系系统的动力学模型中引入了系绳的弹性因素,研究系绳的弹性因素对绳系系统(轨道面内运动)系留状态稳定性的影响;刘延柱和彭建华[14]研究了由系绳的弹性因素引起的纵向振动与绳系系统姿态运动的耦合问题,利用Melnikov方法和Poincare截面的计算证明了绳系卫星具有不可预测的混沌行为;于绍华等[15]基于偏微分方程建立了系留状态下的柔性有质量分布系绳的绳系系统的动力学模型,并通过递推算法求解了系统的定常运动及驻形.然而,这些研究大都针对复杂绳系系统的某一因素或特定的任务需求,不能很好地满足绳系辅助离轨任务的需要.
本文以绳系辅助离轨系统为背景,在上述研究基础上,考虑系绳质量和柔弹性因素,通过分析柔性系绳的受力和运动方式,利用微元法建立展开状态下柔性绳系辅助离轨系统的动力学方程以及边界条件;针对动力学方程复杂的非线性和强耦合问题,采用伽辽金法进行离散化求解及分析,并通过数学仿真来验证和分析柔性绳系辅助离轨系统的展开动力学特性.
1 柔性系绳建模
1.1 基本建模假设
根据所研究问题的特殊性以及为了减轻实际系统的计算压力,结合国内外研究资料[2-4],做出如下合理性假设:
1)空间站和返回飞行器为质点;
2)空间站与返回飞行器质量比很大,在绳系辅助离轨系统的展开过程中,系统的质心和运动中心重合,且时刻在空间站质心处;
3)系统运行在开普勒圆轨道;
4)系绳为理想柔性,不能抗压也不能抗弯.
1.2 相关坐标系
1)轨道坐标系OXYZ.以空间站质心O为原点,建立空间站轨道坐标系OXYZ,如图1所示,Y轴指向地心方向,X轴与空间站轨道面法线平行且与北极方向相反,Z轴与X、Y轴构成右手坐标系,对于圆轨道情况,Z轴指向空间站轨道切向方向.
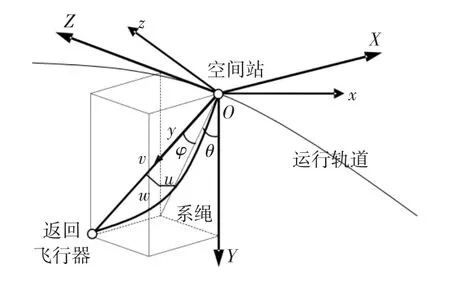
图1 绳系系统的相关坐标系
2)固连坐标系Oxyz.y轴沿空间站和返回飞行器连线方向且指向返回飞行器,x轴与绳系辅助离轨系统的轨道面法线平行且与北极方向相反,z轴与x轴和y轴构成右手坐标系,θ和φ分别为系统的轨道面内、外摆角,u(y,t)、v(y,t)、w(y,t)分别为沿y轴方向,与原点O距离为y的微元dy沿x、y、z方向的位移,其中u(y,t)、w(y,t)为微元的横向位移,v(y,t)为微元的纵向位移或伸展量.
1.3 动力学建模
由上述定义可得,与原点O距离为y的微元dy的位置矢量R为
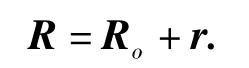
其中Ro为空间站的位置矢量,
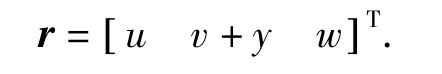
则微元的惯性加速度aI为
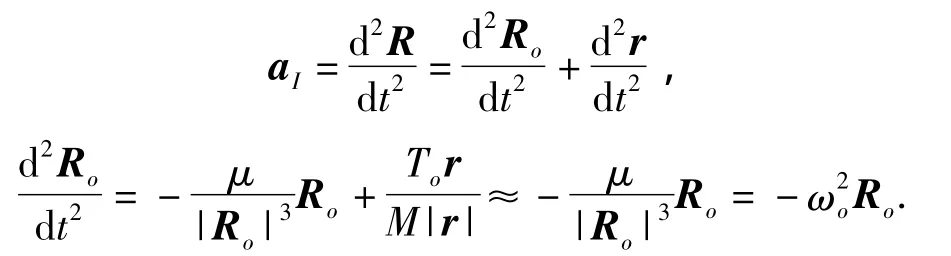
坐标系Oxyz是动坐标系,它的角速度矢量为
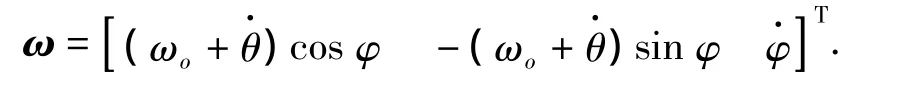
从而可得
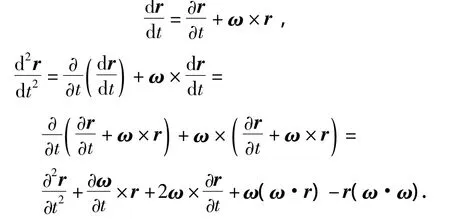
而微元的重力梯度力FG为
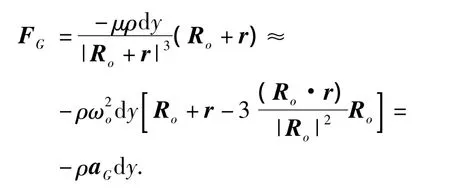
则微元总的加速度a为

微元的径向形变为
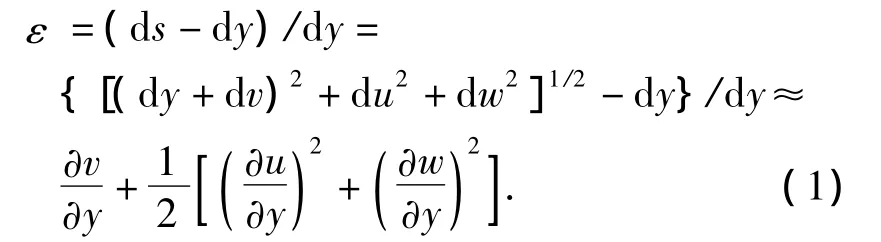
其中ds,dy分别对应伸长后和未伸长的系绳微元的长度.
则微元dz处的系绳张力T为
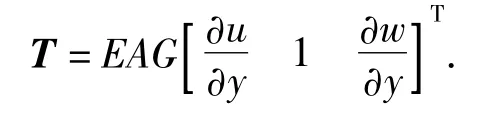
其中

由牛顿运动原理可得微元的受力平衡方程为
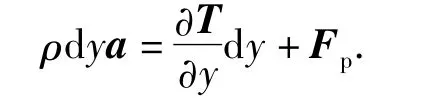
其中Fp为微元所受的空间摄动力,则利用数学变换等可得微元的动力学方程如下


其中边界条件为

1.4 基于伽辽金法的动力学方程求解及分析
上述方程为复杂的非线性、非自治强耦合方程,难以直接进行求解,因而采用伽辽金法[16]进行离散化处理以求解.
基于伽辽金法,构造微元的横向运动位移的近似函数为

其中:φi(y,L)为任意阶的基函数;n表示基函数的项数;Ai(t)、Bi(t)表示特定的系数.根据式(2)~(4)的边界条件,构造微元的横向运动位移的基函数为
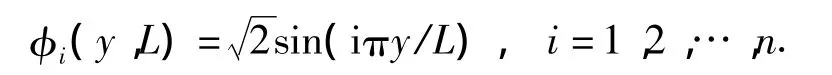
其中,系数Ai(t),Bi(t)是无量纲的时间函数;
φi(y,L)是显含L的函数,因而也是时间的函数,由伽辽金法可得

由于纵向位移的边界条件不同,因而对于微元纵向位移构造特殊的近似函数为
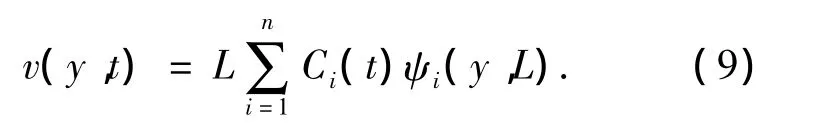
其中系数Ci(t)是无量纲的时间函数;ψi(y,L)是显含L的函数,因而也是时间的函数,根据式(5)的边界条件,构造纵向运动位移的基函数为

由伽辽金法可得
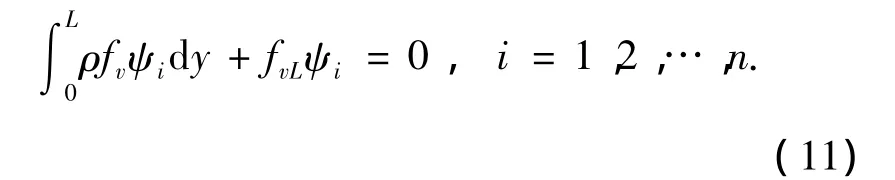
为了更好的分析柔性系绳展开运动特性,在基本假设的前提下采用进一步的假设:
1)绳系辅助离轨系统没有摆动运动或可控—相对某一平衡位置作微幅的振荡(以静态释放模式为例,即θ=φ=θ·=˙φ=ε,L·/L=D,D和ε为小量);
2)C1≫Ci,i=2,3,…,n;
3)与返回舱质量相比,系绳质量可以忽略,不考虑外界摄动作用.
基于上述假设,采用二阶伽辽金模型,由式(7),(8)和(10)可得展开状态下的柔性绳系辅助离轨系统的横、纵向运动的系数方程为
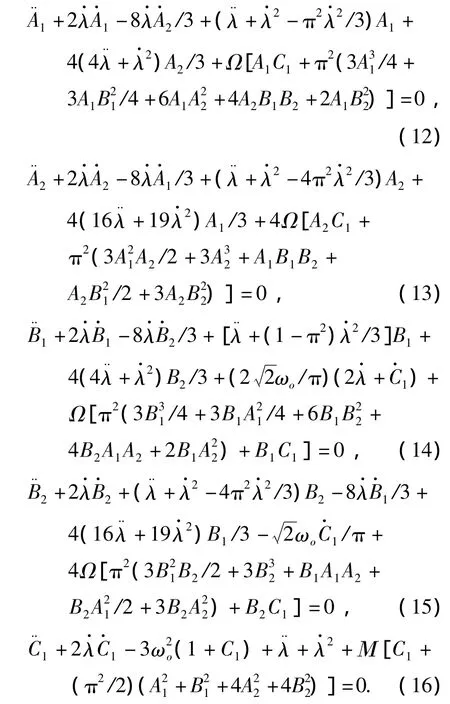
其中Ω=π2EA/ρL2,Μ=EA/msL,λ=lnL.
显然由式(11)和(12)可得,绳系辅助离轨系统的纵向运动和轨道面内横向运动不会引起轨道面外的横向运动,反之不能成立,这与理想情况下的绳系系统的展开运动特性吻合[8],从而柔性绳系辅助离轨系统的展开动力学可以简化,并舍去高阶项得到系数方程为
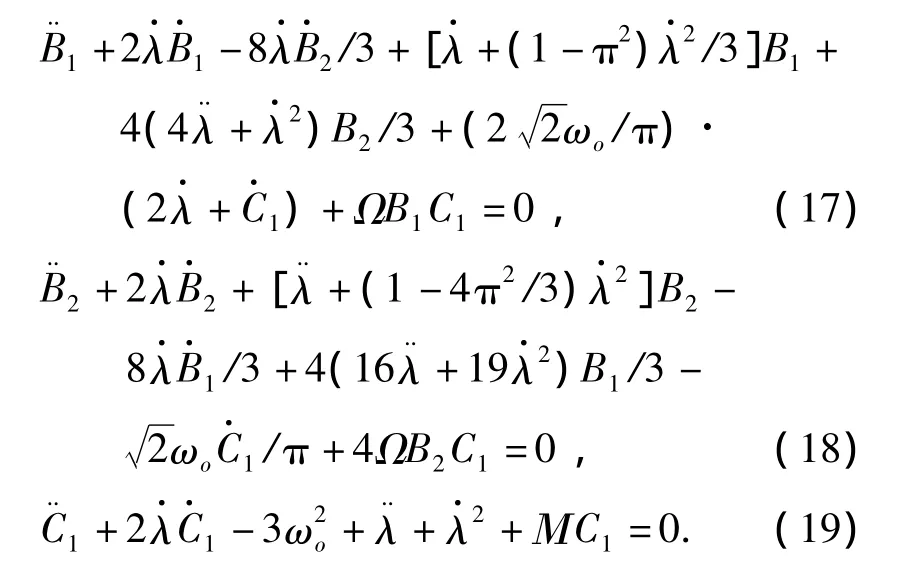
从式(19)可得,系统的纵向运动是一个近似的有激励的二阶阻尼系统,系统的激励为,阻尼系数为,固有频率为而由于采用静态释放,则,系统可以简化为幅值为的阶跃激励下的二阶阻尼系统,则可得纵向运动的系数方程为

2 数学仿真及分析
由于幂指数展开释放规律(L·/L=D,D为常数)可以近似实现绳系系统相对某一平衡位置进行稳定的展开释放[17],可以很好地满足1.4小节的假设条件,因而采用幂指数展开释放规律.选取合适的初始参数以及结构参数,如表1所示,通过数学仿真来验证和分析展开状态下的柔性绳系辅助离轨系统的动力学特性,仿真结果如图2~7所示.

表1 初始参数及结构参数
从图2和图3可以看出,随着系绳的展开长度的不断增加,端体或系统的轨道面内的摆角的振动幅值不断衰减,即系统的轨道面内的横向振动运动不断衰减,系统逐渐趋于稳定的空间驻形;而从图4和图5可以看出,随着系绳展开长度的增加,系统的横向和纵向位移不断增大,但振动幅值不断衰减,即系统的振动运动不断衰减,与1.4节理论分析结果吻合;从图6和图7可以得到,系绳的横向和纵向张力不断增大,且其振动幅值也不断衰减,显然在一定程度上也验证了图4和图5的仿真结果.

图2 绳系辅助离轨系统的展开长度

图3 绳系辅助离轨系统的轨道面内摆角
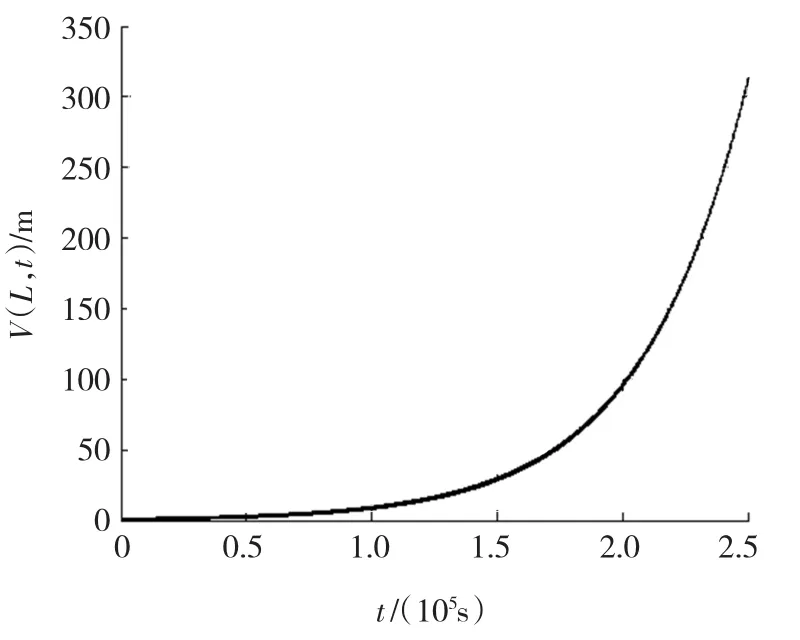
图4 系统的纵向运动(y=L)
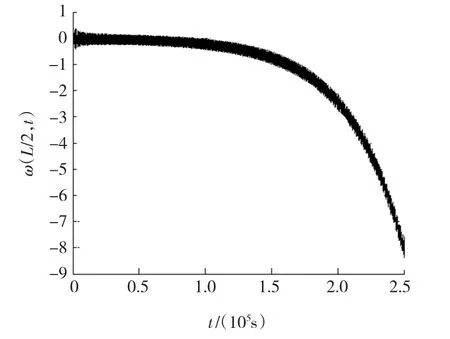
图5 系统的横向运动(y=L/2)
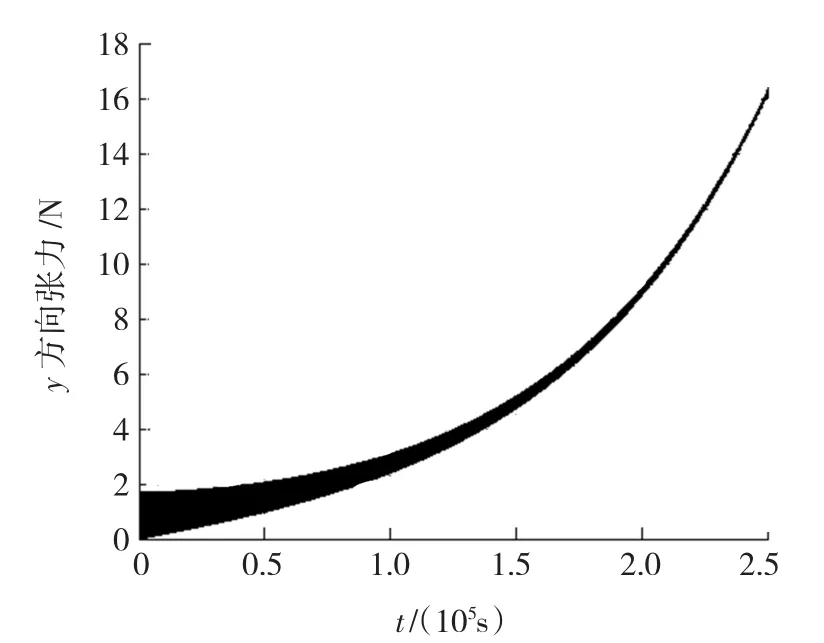
图6 系绳的纵向张力(y=L)
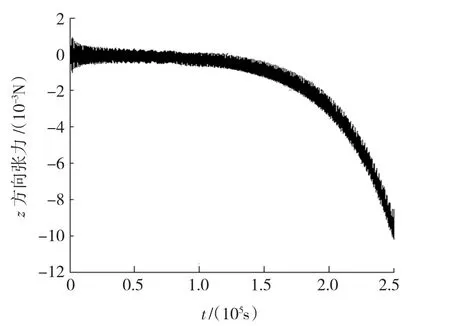
图7 系绳的横向张力(y=L)
综上所述,可以得出,系绳的展开长度对绳系辅助离轨系统的横向和纵向运动影响很大;随着展开长度的增加,系绳的张紧力逐渐增大,从而导致系统的横向和纵向运动的位移逐渐增大,与式(1)吻合,但振动幅值不断衰减,表明系绳张紧力对系统的横向和纵向的振动运动有抑制作用,使系统逐渐趋于稳定的空间驻形.
3 结论
以绳系辅助离轨系统为背景,基于微元法建立了柔性有质量分布系绳的绳系辅助离轨系统的展开动力学模型;针对模型复杂的非线性和强耦合问题,采用伽辽金法进行离散化处理和求解,在此基础上利用二阶阻尼系统的阶跃响应函数,对离散化的模型进行适当的理论分析;并通过数学仿真来验证和分析柔性有质量分布系绳的绳系辅助离轨系统的展开动力学特性.结果表明,系绳的展开长度对绳系辅助离轨系统的横向和纵向振动影响很大,随着展开长度的增加,系绳的张紧力逐渐增大,从而导致系统的横向和纵向运动的位移逐渐增大,而振动幅值不断衰减,系统逐渐趋于稳定的空间驻形,进而也表明系绳张紧力对系统的横向和纵向的振动运动有抑制作用.
[1] WALTHER S.New space application opportunities based on the inflatable reentry&descent technology (IRDT)[C]//AIAA International Air and Space Symposium and Exposition:the Next 100 Years.Dayton,Ohio:[s.n.],2003,AIAA-2003-2839.
[2]ZIMMERMANN F,SCHÖTTLE U M,MESSERSCHMID E.Optimal deployment and return trajectories for a tether-assisted re-entry mission[C]//AIAA Atmospheric Flight Mechanics Conference.Portland,OR,USA:[s.n.],1999:433-443.
[3]BURKHARDT J,ZIMMERMANN F,SCHÖTTLE U M. Operational use of guided reentry capsules-system design solutions and mission safety considerations[J].Aerospace Science and Technology,2004(8):635-644.
[4]JIN D P,HU H Y.Optimal control of a tethered subsatellite of three degrees of freedom[J].Nonlinear Dynamics,2006(46):161-178.
[5]KUMAR K,PRADEEP S.Statrgies for three dimensional deployment of tethered satellites[J].Mechanics Research Commtmieatinns,1998,25(5):543-550.
[6]LICATAT R.Tethered system deployment controls by feedback fuzzy logic[J].Acta Astronautica,1997,40 (9):619-634.
[7]VADALI S R,KIMF E S.Feedback control of tethered satellites using lyapunov stability theory[J].Journal of Guidance,Control,and Dynamics,1991,14(4):729-735.
[8]GLÄßEL H,ZIMMERMANN F,BRÜCKNER S,et al. Adaptive neural control of the deployment procedure for tether-assisted re-entry[J].Aerospace Science and Technology,2004(8):73-81.
[9]LANOIX E L M.A Mathematical Model for the Longterm Dynamics of Tethered Spacecraft[D].Canada: McGill University,1999.
[10]PASCA M,LORENZINI E C.Two analytical models for the analysis of a tethered satellite system in atmosphere[J].Meccanica,1997(32):263-277.
[11]NO T S,Jr COCHRAN J E.Dynamics and control of a tethered flight vehicle[J].Journal of Guidance,Control,and Dynamics,1995,18(1):66-72.
[12]BANERJEE A K.Dynamics of tethered payloads with deployment rate control[J].Journal of Guidance,Control,and Dynamics,1990,13(4):759-762.
[13]LIU Liangdong,BAINUM P M.Effect of tether flexibility on the tethered shuttle subsatellite stability and control[J].Journal of Guidance,Control and Dynamics,1989(2):866-873.
[14]彭建华,刘延柱.绳系卫星的混沌运动[J].上海交通大学学报,1996,30(11):32-35.
[15]于绍华,刘 强.有分布质量系绳的卫星系统的动力学[J].宇航学报,2001,22(3):52-61.
[16]杨桂通.弹性力学[M].第一版.北京:高等教育出版社,1998.
[17]于绍华,刘 强.含无质量系绳的卫星系统平面运动和常规动力学[J].空间科学学报,2001,21(2): 172-180.

