小口径非球面透镜模压成形加热加压参数仿真*

尹韶辉,霍建杰,周天丰,朱科军,王玉方,靳 松,余剑武

(1.湖南大学国家高效磨削工程技术研究中心微纳制造研究所,湖南长沙 410082;2.日本东北大学,仙台日本)

小口径非球面透镜模压成形加热加压参数仿真*

尹韶辉1†,霍建杰1,周天丰2,朱科军1,王玉方1,靳 松1,余剑武1

(1.湖南大学国家高效磨削工程技术研究中心微纳制造研究所,湖南长沙 410082;2.日本东北大学,仙台日本)

为了预测某小口径非球面透镜模压成形加热﹑加压的加工参数,建立了模压模型,设置了相应的边界条件,利用有限元软件对加热﹑加压过程进行了数值计算.分析了540～590℃模压温度下D-ZK 3玻璃充型情况,确定该玻璃的适宜模压温度为580℃左右,模压温度越高残余应力越小.分析了580℃模压温度下的加热过程,确定该条件下最短加热时间为155 s左右.模压后,残余应力边缘大中心小;而应变上部大底部小.研究了3组加压速率下残余应力分布,得到了玻璃模压后平均残余应力随加压速率增大而增大的关系.

非球面镜;黏弹性;有限元法;玻璃模压成形

小口径非球面光学玻璃透镜在数码相机、照相手机、车载摄像装置、DVD读取头、显微及望远镜头、CCD摄像镜头以及内窥镜等产品中的需求日趋增长.传统的非球面透镜加工技术,主要采用研磨抛光等加工方法,存在加工周期长﹑加工质量不稳定﹑对工人技术要求高等方面的不足.光学玻璃非球面透镜模压成形技术的普及推广应用是光学行业在光学玻璃零件加工方面的重大革命.玻璃模压成形技术被引入到小口径非球面透镜的加工成形,克服了传统加工方法的不足.目前日美德等已将该技术应用于工业生产,而在中国该技术还处于研发阶段.

非球面透镜模压成形可以分为4个步骤:加热、加压、退火以及冷却脱模[1].模具和毛坯外面被封闭的石英玻璃管包围,红外线透过玻璃壁加热模具和玻璃毛坯.在加热阶段,上下模具保持静止,玻璃和模具温度达到预定模压温度且分布均匀后进入加压阶段.在加压阶段,上模保持静止,下模以恒定模压速率向上运动,这一阶段继续加热以保持温度恒定,当上下模接触时加压阶段结束.在退火阶段,停止加热,下模保持一恒定模压力使玻璃充满型腔.退火后透镜不能有残余应力,因为玻璃残余应力将造成玻璃折射率不均匀,使成像质量降低[2].然后冷却到室温,取出成形透镜玻璃.在整个过程中,模压室内充满氮气,防止空气中的氧气氧化模具,同时氮气兼有调控加热﹑冷却速率的作用.

目前该技术面临的问题主要有:1)模压成形加工参数的选择;2)非球面模具的设计加工;3)透镜在退火阶段的形状预测;4)低软化温度玻璃的研发制造.

1 仿真模型及边界条件

1.1玻璃材料特性

加热﹑加压过程成形参数主要有最优模压温度、最短加热时间、加压速率等,为了预测最优成形参数,本文用MSC.MARC有限元软件对D-ZK 3非球面透镜的成形过程进行了不同参数下的加热和加压有限元仿真.模具和玻璃物理特性参数如表1所示.

玻璃体积与温度的关系如图1所示.玻璃在转变温度(T g)以下时为固体,坚硬易碎,不易模压成形;温度位于转变温度(T g)至软化温度(S P)之间时,玻璃既有弹性也有黏性,属于黏弹性体,便于模压成形;温度高于软化温度时玻璃已变成流体,存在黏模、加热困难、模具寿命低等问题,不适于模压成形.一般将模压温度选择在屈服温度(A t)附近[1].

表1 玻璃和模具材料参数[2-3]Tab.1 Material properties of g lass and molds[2-3]

图1 玻璃体积与温度关系Fig.1 Plot o f volume change against tem perature for glass

在转变温度和软化温度之间玻璃属于黏弹性体,本文采用广义Maxwell模型来模拟黏弹性玻璃.Maxwell模型由一个黏壶和一个弹簧串联而成,多个Maxwell模型并联组成了广义Maxwell模型[4].

模压过程中总应变为蠕变应变与热应变之和:

式中:εa为模压过程中总应变;εc为模压过程中玻璃蠕变应变;εth为模压过程中玻璃热应变.

黏弹性体在高温时应力松弛较快,在低温时应力松弛缓慢[5].但是不同温度下的松弛模量与时间对数关系曲线的形状并没有改变.松弛时间的温度相关性可以用转化函数(Shift Function)α(T)来表示:

式中:τref是参考温度(本文取600℃)下的松弛时间;τi是某温度下的松弛时间.

转化函数写成指数形式:

其中H为材料常数.

1.2 透镜几何形状和模压系统模型

图2是本文采用的双非球面透镜结构图.

图2 双非球面透镜结构图

Fig.2 Designed biconvex aspheric lens

当平面坐标系原点与透镜非球面顶点重合时,非球面AP1和AP2的形状曲线由以下方程确定:

式中:X为横坐标;Z为纵坐标;R为非球面顶点处曲率半径;k为圆锥常数;B 4,B6,B8,B10为非球面系数.AP1,AP2参数值如表2所示.

表2 非球面AP1,AP2参数值[4]Tab.2 Parameter values for AP1 and AP2[4]

假设在模压过程中玻璃体积不变,对模具非球面曲线表达式进行体积分,可以算出玻璃毛坯的体积,从而得到毛坯玻璃球直径为3.66 mm.

本文用MSC◦MARC软件进行不同温度和加压速率下加热加压有限元仿真,建立的模型如图3所示.

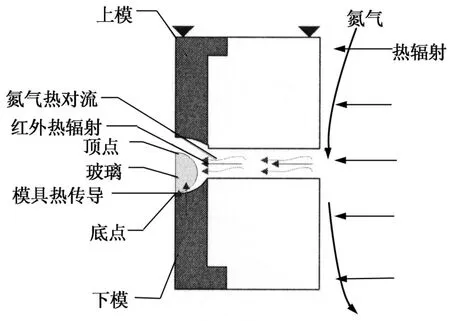
图3 模压系统模型Fig.3 Schematic diagram of themo lding system model

1.3 热边界条件

玻璃热源有3个:1)模具的热传导;2)氮气的热对流;3)红外热源的热辐射.由于玻璃是透明体,热辐射可以忽略[1].在模压阶段玻璃和模具、氮气温度已趋于

一致,可以认为没有热量传递[6].热边界条件为:

式中:K为玻璃热导率;hM为模具与玻璃传热系数; T为玻璃表面温度;T M为模具温度;h N为玻璃与氮气传热系数;TN为氮气温度.hM与接触面压力,接触面温度,摩擦系数等因素有关;h N与氮气流动速度,流动方向,型腔几何形状等因素有关.在现在的实验条件下精确测量h M,h N是不可能的.通常取h M为2 800W/(m2◦K),h N为20W/(m2◦K)[1].

玻璃内部热传导方程为:

式中:ρ为玻璃密度;C p为玻璃比热;t为加热时间.

1.4 摩擦边界条件

模具和玻璃接触面之间的摩擦力可以看成恒剪切摩擦力.

式中:f s为剪切摩擦力;τ为剪切屈服应力;m为摩擦因数,假定玻璃相对模具不发生滑移,可以将m取为1[5].

2 加热加压仿真结果分析

2.1 模压温度的确定

选择模压温度应该考虑3个因素:1)应能保证玻璃充满型腔;2)模压残余应力足够小;3)在保证前2个条件下模压温度要足够低.模压温度过低会造成充不满型腔,残余应力过大,模压力过大;而模压温度过高会造成模具在模压过程中温度变化大,模具寿命降低[4].为了得到合适的温度,在同一加压速率0.1 mm/s下设定模压温度:540～590℃(间隔10℃)仿真对比.

通过对比分析图4,温度在560℃以下玻璃不能充满型腔,而在570℃以上时能充满型腔.所以模压温度应该在570℃以上.

由图5可知,这3组温度下应力云图高亮区域面积从多到少依次是560℃,570℃,580℃,表明平均残余应力随模压温度增大而减小,且在580℃时残余应力已降到10 MPa以下.通过数值拟合得到了540～590℃(间隔10℃)温度下模压温度-最大残余应力曲线如图6所示.

图6表明模压温度越高,最大模压残余应力越小.无论平均残余应力还是最大残余应力都随模压温度的增大而减小.

综上分析,模压温度在580℃左右时,玻璃既能充满型腔,残余应力也不大.在570～580℃模压时玻璃也能充满型腔,但残余应力较大;而在580℃以上时,虽然玻璃流动性更好,残余应力更小,但对模具寿命不利,本文认为该玻璃的模压温度在580℃左右.

图4 当温度为540～590℃时玻璃充型情况Fig.4 G lass filling conditions for differentmolding temperatures from 540℃to 590℃

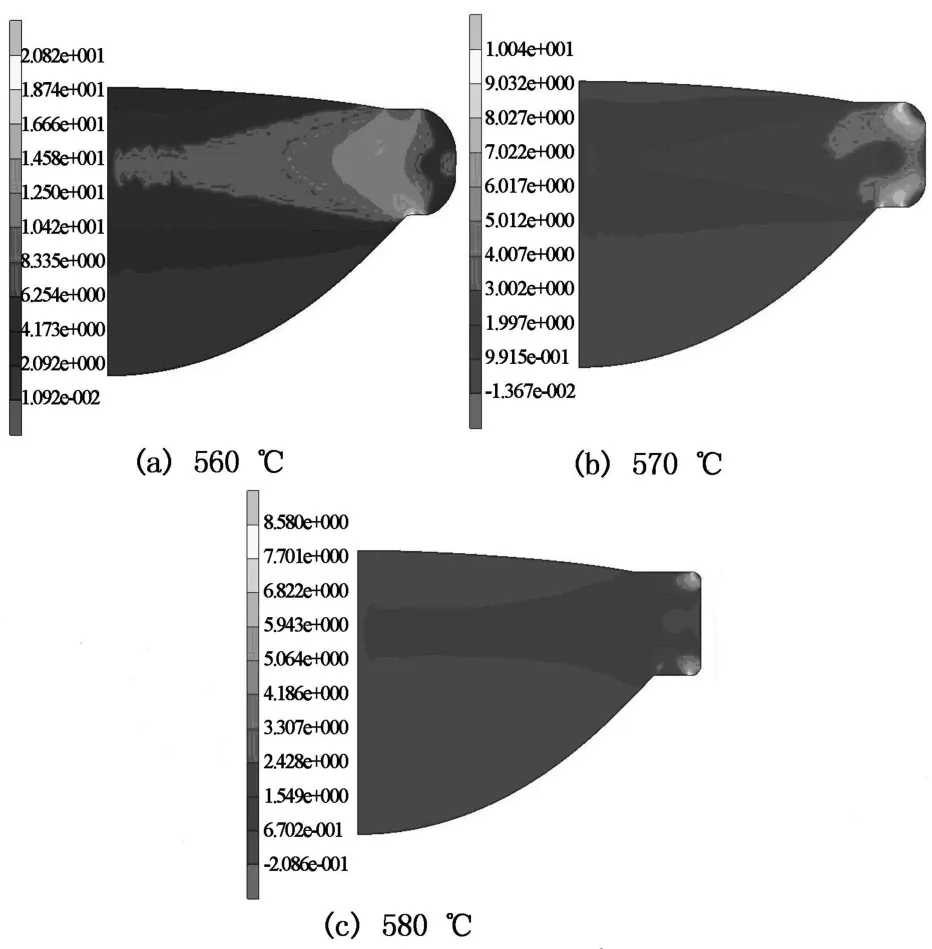
图5 当温度分别为560,570,580℃时残余应力云图Fig.5 Predicted residual stress distribution inside a formed lens for differentmolding tem peratures 560,570 and 580℃

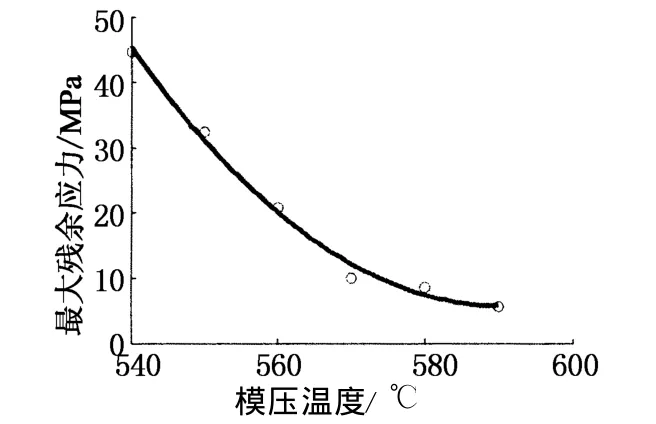
图6 温度-最大残余应力曲线Fig.6 Plot o f themaximum residual stress at differentmolding temperatures

2.2 最短加热时间的确定

最短加热时间指在加热阶段,玻璃温度达到了预定模压温度且分布均匀所需的最小时间.本文预定加热温度为580℃时,进行仿真.如图7所示.

仿真表明:预定加热温度580℃,当加热到155 s时玻璃最小温度已达到579.9℃,可以认为玻璃温度已趋于一致,虽然加热到200 s时所有节点都达到了580℃,但这对缩短生产周期不利.在本文研究的范围内模压温度为580℃时的最短加热时间为155 s.取玻璃最顶点(玻璃温度最低点),最底点(玻璃温度最高点)分析温度随时间的变化历程如图8所示.当加热到155 s时,玻璃顶点和底点温度趋于一致,且底点温度先到达580℃.这也表明在加热过程中玻璃温度底部比顶部升温快.

图7 加热到155 s和200 s时温度云图Fig.7 Temperature distribution inside the glass ballw hen heating for 155 s and 200 s

图8 玻璃顶点﹑底点加热历程Fig.8 Tem perature riseso f the top and bottom nodes during heating p rocess

2.3 加压后玻璃应力应变分析

图9为模压温度580℃,模压速率为0.1mm/s模压后残余应力和应变云图.

图9 当温度为580℃,速率为 0.1mm/s时残余应力与应变云图Fig.9 Predic ted residual stress distribution and strain distribution inside a formed lens after 580℃heating and 0.1 mm/s p ressing

由图9(a)可知,模压过程之后残余应力分布呈现边缘大内部小,上部大下部小的特点.产生这种现象的原因在于在580℃下玻璃近熔融状态,流动性较强,边缘受到模具壁束缚,残余应力较大[7].模压过程中玻璃热量多来自底模,所以下部温度上升快、底部慢,最后趋于均匀.在整个模压过程中,玻璃底部温度平均比上部高,故而残余应力松弛得较快,所以加压后残余应力较小.图9(b)表明模压过程之后玻璃应变呈现上部大下部小的分布特点.模压过程中玻璃从顶部流向边缘形成了非球面.

2.4 加压速率与残余应力关系

为了研究加压速率对模压过程的影响,设定了3组加压速率0.08,0.1和0.12 mm/s,在同一模压温度580℃进行仿真,残余应力云图如图10所示.

图10 当用速率分别为0.08,0.1,0.12 mm/s加压后残余应力云图Fig.10 Predicted residual stress distribution inside a formed lens at differentmolding velocities 0.08,0.1,0.12 mm/s

图10中0.12 mm/s加压时应力云图高亮区域面积最大,依次是0.1 mm/s,0.08 mm/s,随着加压速率的增大,残余应力平均水平呈上升趋势.这主要因为加压速率小,玻璃在高温下就有更多的时间进行应力松弛[8].虽然0.12 mm/s模压残余应力最大值小于0.1 mm/s模压残余应力最大值,但是0.12 mm/s较大残余应力区域比0.1 mm/s大得多.这说明加压速率增大,最大残余应力有可能减小,但其分布区域明显增大,所以平均残余应力较大.当然,加压速率还要考虑模压周期的因素,速率越小周期越大,意味着生产效率降低.

3 结 论

本文对非球面透镜模压成形过程进行了分析,确定了模压成形仿真数学模型、边界条件,并进行了有限元仿真.通过仿真得到了以下结论:

1)通过分析540～590℃模压温度下玻璃充型情况得出该玻璃在570℃以上能充满型腔;模压温度越高残余应力越小.结合考虑模具寿命受温度的影响,确定该玻璃的适宜模压温度为580℃左右.

2)分析了580℃模压温度下玻璃温度随时间的分布云图和温度最高点﹑最低点的加热历程,在本文讨论条件下580℃模压温度的最短加热时间为155 s.

3)通过分析580℃模压残余应力和应变,得出残余应力分布呈现边缘大中心小,上部大底部小的特点;而应变分布呈现上部大底部小,玻璃模压成形过程中材质从顶部流向边缘形成非球面.

4)通过分析不同加压速率下残余应力分布,得出玻璃模压平均残余应力随加压速率增大而增大的关系.

[1] YAN Ji-w ang,ZHOU Tian-feng,MASUDA Jun,etal.M odeling high-temperature glassmolding process by coupling heat transfer and viscous deformation analy sis[J].Precision Engineering,2009,33(2):150-159.

[2] 成都光明光电股份有限公司.光明光电光学玻璃数据库[EB/ OL].(2007-05-08)[2010-05-10].http://www.cdgmgd.com/208/onew s.asp?id=310.

[3] JA IN A,YI A.Num erical simu lation of compression molding of aspherical glass lenses[J].M aterials Processing and Design:Modeling,Simulation and Applications,2004,712:239 -244.

[4] ZHOU Tian-feng,YAN Ji-w ang,YOSHIHARA N,etal.Investigation on the transferability of precision m olding process for aspherical glass lenses[C]//Proceedings of the 8th International Conference on Frontiers ofDesign and Manufactu ring. Tianjin:Tianjin University Press,2008:105-108.

[5] ANANTHASAYANAM B.Computional modeling of precision molding of aspheric glass optics[D].Clemson:The C lemson University,2008:36-39.

[6] JA IN A.Experimental study and numerical analy sis of compression molding process for manufacturing precision asphericalg lass lenses[D].Columbus:The Ohio State University, 2006:7-10.

[7] Y IA,JA IN A.Compression molding of aspherical glass lenses-a combined experimental and numerical analysis[J].Jou rnal of the American Ceram ic Society,2005,88(3):579-586.

[8] JA IN A,YI A,XIE X i-peng,eta l.Finite element modeling of relaxation in glass lensmoulding using measu red,temperature-dependent elasticmodulus and viscosity data of galss[J]. Modeling and Simu lation in Science and Engineering,2006,14: 465-477.

Simulation of the Heating and Pressing Parameters of Micro Aspheric Lens Molding Process

YIN Shao-hui1†,HUO Jian-jie1,ZHOU Tian-feng2,ZHU Ke-jun1, WANG Yu-fang1,JIN Song1,YU Jian-w u1

(1.Institute of Micro-nano Fabrication of National Engineering Research Center for H igh Efficiency Grinding,
Hunan Univ,Changsha,Hunan 410082,China;2.Tohoku Univ,Sendai,Japan)

To predict the heating and pressing parameters of a micro aspheric lensmolding p rocess,a molding processmodelwasestablished and all the boundary conditionswere set.Based on the finiteelementsoftware numerical simulation,mold filling condition ofglass D-ZK3at540～590℃wasanalyzed,and theoptimummolding temperaturewasabout 580℃.The results have shown that the higher themolding temperature,the smaller the residual stress,and theminimum heating time for thismodelisabout155 s at580℃molding temperature.Residual stressaftermolding is larger at the edge of lens than at the center,and the strain is larger at the top than at the bottom.Finally,three differentmolding velocities wereanalyzed,and the results have shown that theaverage residual stress of the lens increaseswith the increase ofmolding velocity.

aspherics;viscoelasticity;finite elementm ethod;g lassmo lding process

TH 164

A

1674-2974(2011)01-0035-05 *

2010-06-01

国家自然科学基金资助项目(50975804)

尹韶辉(1967-),男,湖南湘潭人,湖南大学教授,博士生导师

†通讯联系人,E-mail:shyin2000@hotmail.com