效应量：体育科研中不应忽略的统计量

温 煦

假设检验的理论和方法是量化研究中最常用和最基本的统计方法之一。许多科研工作者在撰写科研论文中习惯于提供假设检验的P值，在阅读论文时往往会注重P值的大小。然而，假设检验也存在许多局限性，比如，P值仅能提供原假设成立与否的概率，且受样本量和标准差的影响。近十年来，越来越多的科研工作者提出，在论文中仅仅报道假设检验的结果容易误导读者，建议采用效应量（effect size）作为假设检验的补充。2001年，美国心理学会（American Psychological Association，APA）论文发表手册规定发表论文必须报道效应量［2，15］。生物学、医学等其他学科的研究者也建议在各自领域的论文中报道效应量［1，13］。然而，我国统计教科书中对于效应量的介绍比较有限，大部分学术期刊也没有要求投稿论文报道效应量［1］。在我国体育科研中同样大量存在仅报道假设检验结果而不报道效应量的现象，可能造成对研究数据的误读。因此，本文旨在简要介绍效应量的作用、计算和评价方法，以期推广效应量在我国体育量化研究中的应用，促进体育科研工作者多角度地分析科研数据，更准确、更客观地报道和解读体育科研成果。

1 效应量的定义、分类和意义

效应量是反映效应程度大小的统计量，代表变量之间的紧密或差异程度［13］。效应量可分为简单效应量、标准化效应量和相关效应量［12］。简单效应量通常是效应组与对照组平均值之差。APA建议，当简单效应量具有实际的实践意义时（如3个月的运动减肥干预可以减少脂肪多少千克），可考虑采用简单效应量［16］。但是，简单效应量受到量纲、整体变异大小等因素限制，不便于研究间的比较。标准化效应量则通过标准化数据解决了这些问题（如Cohen’sd等）。而相关效应量则是指自变量与应变量的相关程度（如决定系数R2等）。许多研究论文往往会报道结果的简单效应量和相关效应量，如在回归方程中应报道决定系数或校正决定系数已成为基本要求。相比较而言，在我国体育类期刊中，很少有论文会报道标准化效应量。

2 假设检验的局限性和报道效应量的必要性

假设检验是判断样本与样本、样本与总体的差异是由抽样误差造成还是由本质差别引起的统计推断方法。假设检验兴起于20世纪，1900年前后仅有10％的心理学实验论文应用了假设检验，而到了1970年，超过70％的实验性论文使用了假设检验［8］。如今，假设检验的基本思想广泛应用于各学科科研工作的统计分析中，是广大科研工作者学习的最重要、最基础的统计方法之一。然而，近年来，作为许多统计检验的“基石”的假设检验理论却受到了许多专家学者的质疑、挑战甚至全盘否定［3，4，6，7］。假设检验被质疑的问题很多，本文不作赘述，但是，其中两条应引起注意。第一，假设检验的最终结果一般只有拒绝原假设（P＜0.05或P＜0.01）和未能拒绝原假设（P＞0.05）两种。这种“非此即彼”的二分类式判断，不仅忽略了P=0.06与P=0.99的区别，损失了大量信息，还容易因此引起对于统计结果的误用和误读。第二，样本量和标准差的大小很大程度上会影响假设检验的结果。比如，在需要判断两组运动员的血红蛋白的差异是否有统计学意义时，常常采用独立样本t检验。值得注意的是，只要两组运动员的血红蛋白水平差异足够大，即使两组运动员样本比较小，组内标准差比较大，统计上两组差异会具有显著性；相反，即使两组运动员血红蛋白水平差异很小，但只要样本量足够大，组内标准差足够小，统计结果仍会显示两组差异具有显著性。因此，同样的统计结果，所包含的实际意义却大不相同。Gliner等学者总结了假设检验在应用中存在的两大误区：一是，以P值大小来判断变量间关系的强弱；二是，将统计的显著性等同于理论或实践中的显著性［7］。

假如采用效应量作为假设检验的补充，以上问题就可以得到较好的解决，也有利于解决假设检验结果的误用和误读问题。此外，近年来被广泛应用的荟萃分析（meta-analysis）其核心思想也是要综合考虑一组相关研究的效应量。假如今后所有的科研论文都报道效应量，必然有利于日后学者进行荟萃分析，总结研究结果，促进学科的整体发展。

3 效应量的种类和计算方法

据不完全统计，针对不同的统计方法所建立的效应量超过60种［9］。随着效应量报道在各学科期刊的推广，如何合理选择和计算效应量将成为广大科研工作者面临的问题。鉴于篇幅原因，本文仅介绍几种在其他学科已经广泛采用，但在体育科研中却应用较少的效应量及其计算方法。

Cohen’sd是最常用的标准化效应量之一，其定义为两组平均值之差除以标准差（方程1），可应用于两组样本均数比较的效应量计算。在这里，Cohen定义的标准差是任意一组标准差（因为两组标准差被假定为相等）［5］。在实际计算中，大多数学者推荐采用合并标准差（Pooled Standard Deviation），计算方法如方程2所示。在标准差未知的情况下（如需要了解某论文结果部分的效应量，但该论文未提供标准差等），也可以通过其他方法（如方程3）进行估计［11］。Cohen’sd的评价标准为：小效应（≧0.2且＜0.5）；中等效应（≧0.5且＜0.8）；大效应（≧0.8）。其他学者也提出过其他的评价标准［13］，但只是临界值略有不同，如临界值分别为0.15、0.4和0.75。

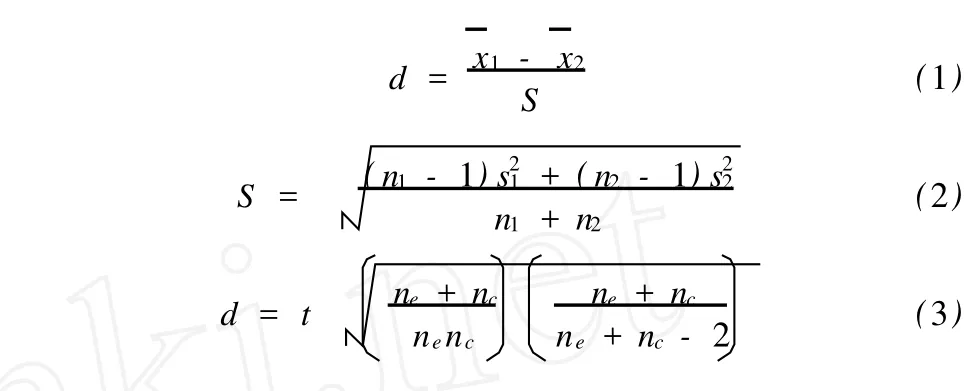
与Cohen’sd相类似的效应量还有Glass’s Delta（Δ）和Hedges’s g。Glass’s Delta是两组平均值之差除以第2组（或对照组）的标准差（方程4）。Hedges’s g也是两组平均值之差除以合并标准差，但公式中合并标准差的计算与Cohen’sd略有差异（方程5）。

η2（eta squared）是方差分析中常用的效应量，代表应变量被某一自变量解释的方差比例（方程6）。由方程可知，η2受自变量数目所影响。当自变量数目增加时，η2会减小，因而无法准确评价效应的大小。因此，有学者提出了（partical eta squared）。是控制了其他自变量后应变量被某一自变量解释的方差比例（方程7），一般而言，＞η2（单因素方差分析时，两者相同）。由于的分母是效应变异和误差变异的和，不会因为自变量的增多而变化，从而有利于评价。需要注意的是，也因此各自变量的之和不等于1。某些统计软件，如SPSS提供了计算多因素方差分析的的功能模块。有学者建议的评价标准为：小效应（≧0.01且＜0.06）；中等效应（≧0.06且＜0.14）；大效应（≧0.14）［10］，但目前尚无统一的评价标准。

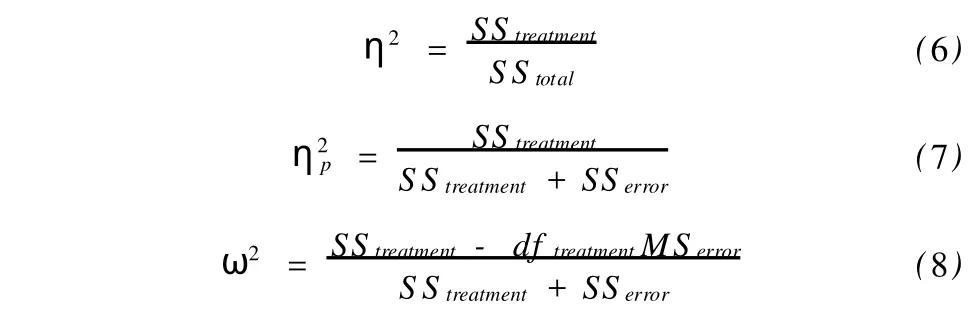
φ（phi）是卡方检验中的常用的效应量，其计算方法如方程9所示，其中，χ2是卡方值，n是样本量。但φ只能用于计算2×2四格表卡方检验中的效应量，对于多行多列的情况，应采用φc（Cramér’s phi），其计算公式如方程10所示，其中，k为行数和列数中的较小者（如3×4表格中，k=3）。

4 效应量在我国体育量化研究中的应用情况

为了进一步了解效应量在我国体育量化研究中的应用情况。本研究以《体育科学》2009年公开发表的学术论文为研究对象，汇总了其中涉及统计计算中所应用的统计方法以及效应量的应用情况。结果显示，2009年12期《体育科学》共刊载论文165篇，其中71篇论文采用了统计分析（不包括仅应用了描述性统计的论文），具体的统计方法如表1所示。单因素方差分析和t检验仍然是我国体育科研中最常用的统计方法，遗憾的是，采用这两类方法的研究者均没有报道研究结果的效应量。在5篇采用多因素方差分析的论文中，仅有一篇论文报道了效应量η2。而对于相关分析、回归分析等其他统计方法，报道相关系数、决定系数等效应量已成为基本要求，因此，不再进行汇总统计。统计结果反映了大部分体育科研论文中没有报道效应量。原因可能有：1）许多科研工作者对效应量相关知识了解有限，大部分中文统计书也没有专门介绍效应量的计算和应用方法；2）许多科研工作者还没有形成报道效应量的习惯。值得注意的是，很少有科研工作者会在相关分析中只报道假设检验的P值而不报道相关系数（相关系数也是一种效应量），但是大部分人却不习惯于在t检验中既报道P值，也报道Cohen’sd。事实上，在t检验中报道Cohen’sd应该与在相关分析中报道相关系数同样重要。

表1 2009年《体育科学》刊载论文采用统计方法汇总一览表

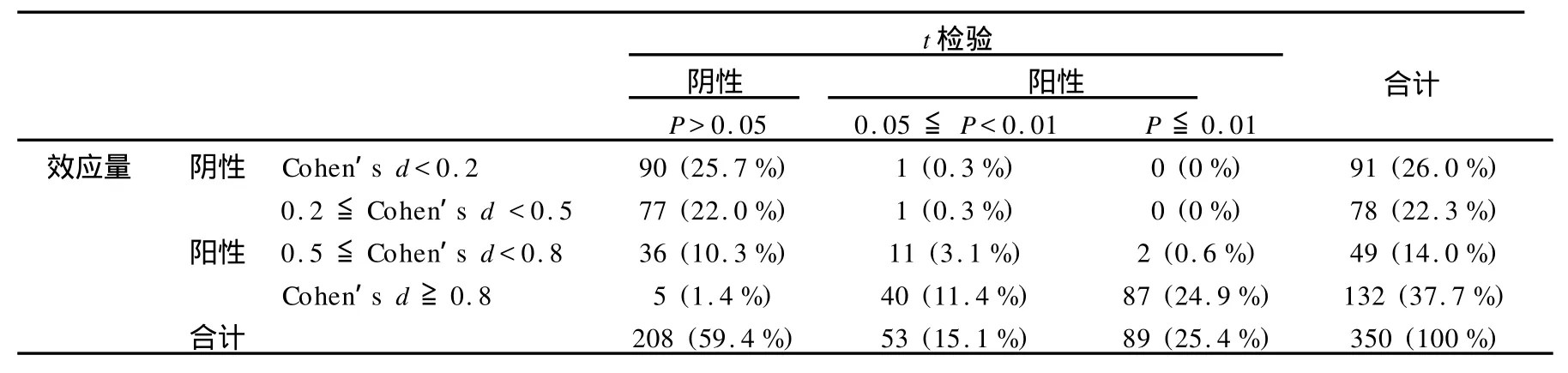
表2 2009年《体育科学》刊载论文中t检验统计结果所对应的效应量汇总

为进一步探讨报道效应量的意义，笔者按照公式1和公式2，根据2009年《体育科学》刊载的20篇采用t检验论文所报道的数据（平均值、标准差、样本量），计算其t检验结果所相对应的效应量Cohen’sd的值，并进行归类，t检验和效应量阴性和阳性结果的临界值分别设为P=0.05和Cohen’sd=0.5。需要说明的是，由于其中2篇论文所报道的信息不全，最终只计算了18篇论文共计350次t检验结果的效应量。选择t检验和Cohen’sd作为例子，主要是基于两个原因：1）t检验是最常用的统计方法之一；2）Cohen’sd计算所需的平均值、标准差、样本量，大部分论文会报道，方便计算。而其他统计方法的效应量计算所需数据（如方差等）在论文中往往不做报道。

分类统计的结果如表2所示，假如以效应量统计结果作为参照，则t检验发生I型错误的概率为0.6％（2/350），出现II型错误的概率为11.7％（41/350）。这意味着，t检验和效应量结果是不完全一致的，超过12％的t检验结果可能存在问题。在量化研究中，科研论文的结论建立在统计结果的基础上。因此，即使只有12％的统计结果有误，也可能颠覆许多论文的结论。本研究的结果提示，有必要重新审视假设检验的统计结果。

t检验结果可能出现的偏差可以分为“假阴性”和“假阳性”两类。第一，样本量不大时，t检验可能敏感度不高，未能检测到原本存在的差异，出现假阴性错误。原因可能是，当效应量大但样本量不大时，t检验判断差异由抽样误差引起，因而“忽视”了差异的存在。第二，当样本量比较大时，t检验“放大”了某些比较小、甚至实际并不存在的差异，出现假阳性错误。原因可能是，大样本量影响了t检验计算的计算结果。而Cohen’sd则是从数据实际的平均值差异和数据变异的角度去观察两组数据的差异。因此，在假设检验的基础上，增加效应量这个统计量，能够帮助科研工作者从过去单一的“假设检验”角度，到从“假设检验”和“效应量”两个角度去研究数据，更有利于厘清数据的真实情况，从而做出更准确、更客观的判断。

5 效应量的不足

虽然许多专家、学者都建议用效应量作为假设检验的补充，甚至建议用效应量代替假设检验［3，6］，但是，效应量本身也存在一些不足。比如，采用效应量进行统计判断的体系仍不完善，很多效应量也还没有建立统一的评价标准。这给效应量的应用带来了许多问题，仍需要进一步的研究加以完善。此外，由于效应量计算中缺乏对样本量的考量，单一依靠效应量进行统计判断必然受到抽样误差影响。因此，正视假设检验和效应量的不足，综合考量效应量和假设检验的结果，可能是现阶段比较合理的统计分析策略。

6 小结

统计方法的发展在一定程度上可以促进学科的发展，而统计方法上的落后在一定程度上也会制约学科的进步。假设检验在我国体育科研领域已经得到了广泛应用，但假设检验本身的确存在一些局限，而效应量可以作为假设检验有益的补充。近年来，效应量引起了越来越多专家、学者的重视，心理学、生物学、医学等学科的许多国际学术期刊已经开始要求稿件提供效应量。可以预见，报道效应量应该是今后统计分析的发展趋势，也是体育科研中不应忽略的统计量。在我国体育科研工作中，加强效应量方面的教育培训和应用实践，并在我国体育类期刊中倡导报道效应量将有助于更客观、更准确地报道体育科研成果。

［1］李运明，袁天峰，陈长生，等.医学研究方差分析模型中效应量的探讨［J］.第四军医大学学报，2008，29（3）：266-269.

［2］AMERICAN PSYCHOLOGICAL ASSOCIATION.Publication Manual of the American Psychological Association（5th edition）［M］.Washington，DC，2001.

［3］ANDERSON D R，BURNHAM K P，THOMPSON W L.Null hypothesis testing：Problems，prevalence，and an alternative［J］.J Wildl Manage，2000，64（4）：912-923.

［4］ARMSTRONGJ S.Significance tests harm progress in forecasting［J］.Int J Forecast，2007，23（2）：321-327.

［5］COHEN J.Statistical Power Analysis for the Behavioral Sciences（2nd edition）［M］.Hillsdale，NJ：Erlbaum，1988.

［6］COHEN J.The earth is round（P＜0.05）［J］.Am Psychol，1994，49（2）：997-1003.

［7］GLINER J A，LEECH N L，MORGAN G A.Problems with null hypothesis significance testing（NHST）：What do the textbooks say？［J］.J Exp Edu，2002，71（1）：83-92.

［8］HUBBARD R，RYAN P A.The historical growth of statistical significance testing in psychology—and its future prospects［J］.Edu Psychol Meas，2000，60（5）：661-681.

［9］HUBERTY C J.A history of effect size indices［J］.Edu Psychol Meas，2002，62：227-240.

［10］KITTLER J E，MENARD W，PHILLIPS K A.Weight concerns in individuals with body dysmorphic disorder［J］.Eat Behav，2007，8（1）：115-120.

［11］LEDESMA R D，MACBETH G，DE KOHAN N C.Computing effect size measures with ViSta-the visual statistics system［J］.TQMP，2009，5（1）：25-34.

［12］MELINE T，WANG B.Effect-Size reporting practices in AJSLP and other ASHA journals，1999-2003［J］.Am J Speech Lang Pathol，2004，13（3）：202-207.

［13］NAKAGAWA S，CUTHILL I C.Effect size，confidence interval and statistical significance：a practical guide for biologists［J］.Biol Rev Camb Philos Soc，2007，82（4）：591-605.

［14］OLEJNIK S，AL GINA J.Generalized Eta and Omega Squared Statistics：Measures of Effect Size for Some Common Research Designs［J］.Psychol Methods，2003，8（4）：434-447.

［15］VACHA-HAASE T，NILSSON J E，REETZ D R，et al.Reporting practices and APA editorial policies regarding statistical significance and effect size［J］.Theory Psychol，2000，10：413-425.

［16］WIL KINSON L，TASK FORCE ON STATISTICAL INFERENCE.Statistical methods in psychology journals：Guidelines and explanations［J］.Am Psychol，1999，54（8）：594-604.