基于二元语义的非常规突发事件群决策方法

岳小云,郑国萍

(河北科技师范学院数学与信息科技学院,河北秦皇岛,066004)

所谓突发事件是指突然发生,造成或者可能造成重大人员伤亡、财产损失、生态环境破坏和严重社会危害,危及公共安全的事件[1]。而非常规突发事件是指与传统突发事件相比,前兆不充分,具有明显的复杂性特征和潜在危害,破坏性严重,采用常规应急管理方式难以应对管理的突发事件[2]。近年来,这类突发事件越来越频繁地袭击着人们生存的世界[3]。与此同时,近年来我国地区非常规突发事件的频发度及危害性也呈明显的上升趋势。2008年以来,我国分别经历了南方雨雪冰冻灾害、“3.14”拉萨打砸抢烧事件、“5.12”汶川特大地震、“3.28”山西王家岭煤矿透水事故、“4.14”玉树地震、“8.24”伊春空难等。因此,必须把非常规突发事件作为一项重要而紧迫的任务,做好相关的应急管理决策,有效地应对这类罕见非常规突发事件带来的威胁。

认识非常规突发事件应急管理决策有利于提高决策准确性和事件处理效率,发挥应急管理的整体效能。构建科学的非常规突发事件应急决策系统是建立完善有效应急管理体系的关键所在。国内外学者对突发事件应急决策相关研究较多。例如,唐伟勤等[4]针对地区资源布局问题,通过构造资源需求-供给函数,评估已有资源布局对地区需求的保障程度,建立了资源布局优化模型;徐高[5]、何建敏等[6]、缪成等[7]就人员紧急疏散问题,构建仿真模型,优化应急决策过程中调度管理;徐志新等[8]对核事故应急决策问题进行研究,提出该类问题决策的多属性效用方法。目前,非常规突发事件研究主要侧重于解决某些具体的应急决策问题,而用群决策方法研究论文很少。

由于非常规突发事件的复杂性和不确定性,有时决策者无法给出精确的决策数据,许多决策者更喜欢用语言表达自己的意见。笔者利用国际上最新发展的基于语言评价信息的二元语义群决策方法进行决策评价。在评价过程中,考虑到专家对非常规突发事件认识程度的不同,对各个方案和属性的评分标准和角度不同,选择了不同粒度的语言术语集,这样每个专家在评价决策过程中,可以根据其偏好提出不同语言信息。

1 二元语义信息及其集结算子[9～11]

二元语义信息是由西班牙的 Herrera教授在 2000年提出的。这种方法将语言短语看作是其定义域内的连续变量,它能以预定的语言短语集中的一个短语和一个实数值的二元形式来表达语言评价信息集成后所获得的所有信息,可有效避免语言评价信息集结和运算中出现的信息损失和扭曲,也使语言信息计算结果更为精确[9～12]。

二元语义是采用一个二元组(sk,ak)表示语言评价信息的方法。其元素 sk和 ak的含义描述如下:

(1)sk为预先定义好的语言评价集 S中的第 k个元素。例如 S={s0=FC(非常差),s1=HC(很差),s2=C(差),s3=YB(一般),s4=Z(重要),s5=HZ(很重要),s6=FZ(非常重要)}。

(2)ak称为符号转移值,满足 ak∈[-0.5,0.5),表示评价结果与 sk的偏差。

定义 1 若 sk∈S是一个语言短语,那么,相应的二元语义形式可以通过下面函数 θ获得

定义 2 设实数 β∈[0,T]为语言评价集 S经某集结方法得到的实数,其中,T+1为语言评价集 S中元素的个数,称为粒度,则 β可由如下函数 Δ表示为二元语义信息

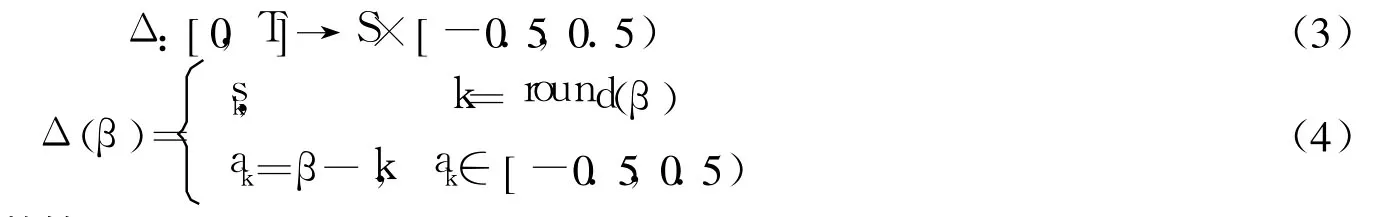
其中,round为四舍五入取整算子。

定义 3 设(sk,ak)是一个二元语义,其中 sk为 S中第 k个元素,ak∈[-0.5,0.5),则存在一个逆函数 Δ-1,使其转换成相应的数值 β∈[0,T]

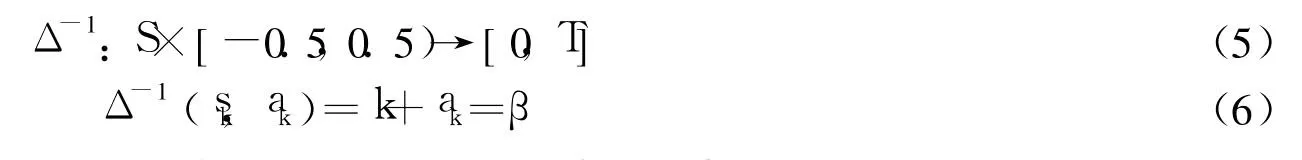
假设(sk,ak)和(sl,al)为两个二元语义,关于二元语义的比较有如下规定[7]:

(a)若 k＜l,则(sk,ak)≺(sl,al),这里符号“≺”表示劣于;

(b)若 k=l,①ak=al,则 (sk,ak)=(sl,al);②ak＜al,则 (sk,ak)≺(sl,al);③ak＞al,则 (sk,ak)≻(sl,al)。

定义 4 设{(s1,a1),(s2,a2),…,(sn,an)}是一组二元语义信息集合,则有序加权平均(T-OWA)算子定义为

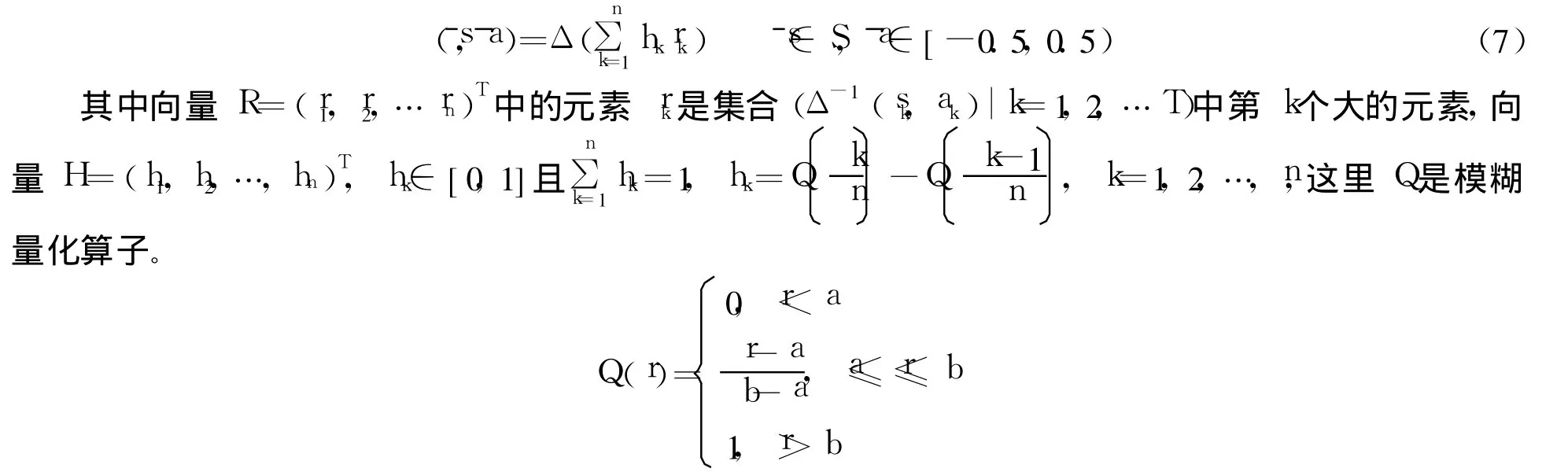
式中 a,b,r∈[0,1]在“至少一半”、“模糊多数”和“尽可能多”的原则下,模糊量化算子 Q对应的参数[a,b]分别为 (0,0.5),(0.5,0.8)和(0.5,1)。

定义 5 设{(s1,a1),(s2,a2),…,(sn,an)}是一组二元语义信息,相应的权重向量为={(1,β1),(2,β2),…,(n,βn)}T,则二元语义加权平均(T-WA)算子定义为

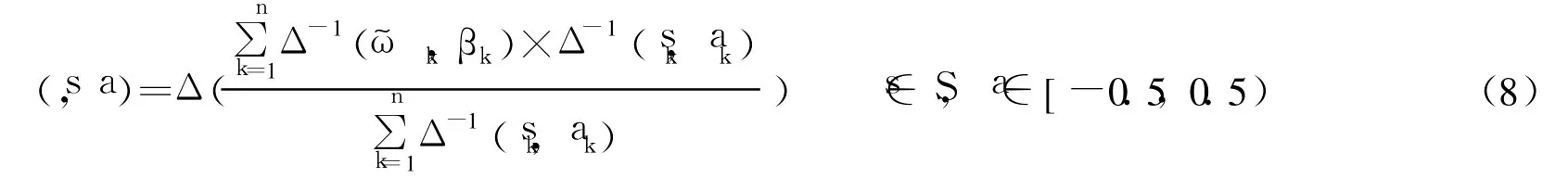
2 多粒度二元语义的群决策评价方法

2.1 问题描述

考虑一个从多个备选方案中选出最优方案或对方案进行排序的非常规突发事件应急处理的群决策问题:假设由 m个方案,n个属性和 t位决策者组成。方案集为A={A1,A2,…,Am}(m≥2),属性集为 G={G1,G2,…,Gn},决策者集为 E={E1,E2,…,Et},不同粒度的语言评价集合分别为 S1,S2,…,Sp。设决策者 Ek∈E对于方案 Ai∈A关于属性 Gj(j=1,2,…,n)给出评价信息∈ Sq,Sq∈ {S1,S2,…,Sp},其中 p=1,3,…,从而构成语言决策矩阵 Rk=()m×n,ω=(ω1,ω2,…,ωn)T表示评价属性的权重向量,其中 ωj表示属性 Gj的权重,满足

2.2 二元语义的一致化处理

在非常规突发事件方案决策中,当专家给出的是多粒度的语言评价集时,首先需要将专家给出的语言信息进行一致化,以便进行群的集结和方案优选。一致化时,据基本语言变量集合(BLTS)选择原则,选粒度最高的语言变量集作为基本语言变量集合。在此采用语言变量转换函数(T将多粒度语言评价信息转为由 BLTS表示的二元语义形式[13],转换函数保证了语言变量在各层级之间转换的过程中无信息丢失。语言变量转换函数 T具体形式为 :

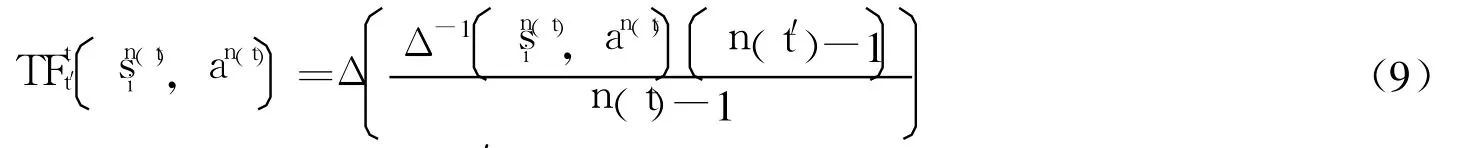
其中 n(t)为专家所处的语言术语集的粒度 n(t′)为基本语言评价集的粒度。

2.3 群集结和方案优选的步骤

据 2.2给出的多粒度语言信息一致化处理方法,给出基于多粒度二元语义信息的非常规突发事件群决策方法。具体步骤如下:

Step1 给出每个专家的语言决策矩阵和语言权重向量,并将其转化为二元语义形式矩阵。利用式(1)～(3)将语言评价信息转换成二元语义。

Step2 将多粒度二元语言信息一致化处理。首先从多个语言集中选一个 Sq作为 BLTS。然后,根据转换函数 TFtt′式(9),将多粒度语言信息的评价矩阵和语言权重向量转换成 BLTS。

Step3 采用 T-OWA算子将所有决策专家的评价矩阵和指标权重向量集结为群的评价矩阵和群的权重向量。

Step4 计算每个备选方案群体综合评价值,使用二元语义加权算术平均算子获得每个备选方案的综合评价值。

Step5 进行方案优选。根据方案排序情况选出最优方案。

3 算 例

假设某非常规突发事件有 4个资源配送方案可供选择,方案分别为 A1,A2,A3和 A4。在对这 4个备选方案进行排序和优选时,考虑 4个方面的因素,即评价属性分别为:所需时间 G1,道路运输能力 G2,资源储备 G3和资源需求量 G4。选 4位专家进行决策优选,分别为 E1,E2,E3,E4。选 4个不同粒度语言评价集,分别为

考虑专家 E1采用 S5,专家 E2采用 S7,专家 E3采用 S9,专家 E4采用 S11。4位专家分别给出了 4个语言评价矩阵和属性权重的语言评价向量

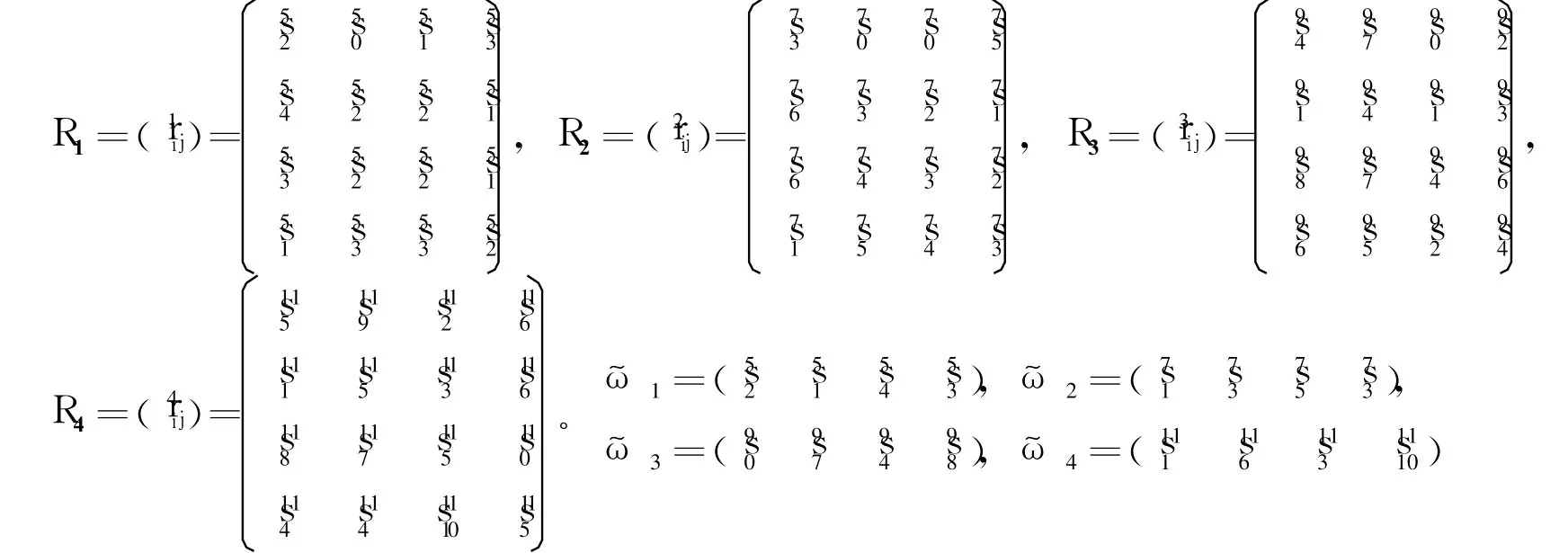
首先,将专家的语言评价信息转化为二元语义形式。由 BLTS选择准则,选 S3为基本语言集。据式(9)将语言评价信息一致化处理,如下:

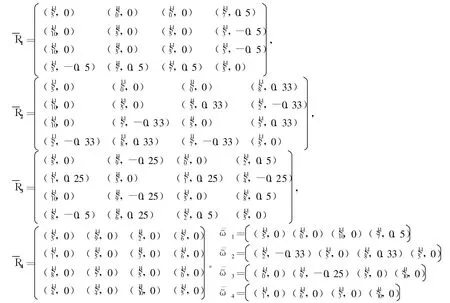
假设决策时采用的是“尽可能多”的原则,使用 T-OWA算子将所有评价矩阵转化为群的综合评价矩阵和权重向量。

4 结 论

本次研究采用的多粒度二元语义信息评价方法,为非常规突发事件的快速方案优选提供了一种方法,与其他方法相比,考虑了如何有效避免信息转化和运算中出现的信息损失和扭曲问题,使决策评价信息集结结果更为精确。算例表明,基于二元语义信息处理的群决策方法具有计算简单,处理语言信息准确等特点,具有一定的有效性和实用性。

[1] 陈晓田.非常规突发事件应急管理研究[R].北京:第三届国际应急管理论坛暨中国双法应急管理专业委员会第四届年会大会报告,2008.

[2] 韩智勇,翁文国,张维,等.重大研究计划“非常规突发事件应急管理”研究的科学背景、目标与组织管理[J].中国科学基金,2009(4):215-220.

[3] 佘廉,吴国斌,吕浩,等.关于我国政府对重大突发事件管理现状的问卷调查与分析[J].中国安全科学学报,2005,15(7):16-20,30.

[4] 唐伟勤,张敏,张隐.大规模突发事件应急物资调度的过程模型[J].中国安全科学学报,2009,19(1):33-37.

[5] 徐高.人群疏散的仿真研究[D].成都:西南交通大学,2003.

[6] 何建敏,刘春林.限制期条件下应急车辆调度问题的模糊优化方法[J].控制与决策,2001,16(3):318-321.

[7] 缪成,许维胜,吴启迪.大规模应急救援物资运输模型的构建与求解[J].系统工程,2006,24(11):6-12.

[8] 徐志新,奚树人,曲静原.核事故应急决策的多属性效用分析方法[J].清华大学学报:自然科学版,2008,48(3):448-451.

[9] HERRER A F,MARTINE Z L.A 2-tuple fuzzy linguistic representation model for computing with words[J].IEEE Transactions on Fuzzy systems,2000,8(6):746-752.

[10] HERRER A F,MARTINE Z L.A model based on 2-tup les linguistic for dealing with multi-granularity hierarchical linguistic contexts in multi-expert decision-making[J].IEEE Transactions on Systems,Man and Cybernetics Part B Cybernetics,2001,31(2):227-234.

[11] 张尧,樊治平.一种基于语言集结算子的语言多指标决策方法[J].系统工程,2006,24(12):98-101.

[12] 巩在武,刘思峰.不同偏好形式判断矩阵的二元语义群决策方法[J].系统工程学报,2007,22(2):185-189.

[13] 王艳琴,刘新旺.基于多粒度二元语义的供应商选择方法[J].价值工程,2008(11):65-68.

(责任编辑:朱宝昌)