切割函数与参数选择的关系
岳崇山,张蒲修
(1.河北北方学院理学院,河北 张家口75000;2.张家口市农业行政综合执法支队,河北 张家口075000)
研究各种平面区域或空间区域的差别有很多种方法.比较几何化的方法是研究平面区域或空间区域的边界曲线或边界曲面.研究平面区域的边界曲线的局部轴对称性是一种重要的方法.使用双切圆 (即给定平面上的简单光滑闭曲线M,研究与M相切不止一点的圆 )来刻画曲线的局部对称性是常用的方法.如果曲线上每一点都存在双切圆,那么就表明平面曲线具有 “局部”的对称性.所有双切圆的中心形成图形称为曲线的对称集.在平面区域的外形识别中,对称集有着非常重要的作用,见参考文献 [1-4].
有许多文献对曲线的双切圆进行了细致的研究,比如Peter J.Gibin和Donal B.O'shea在参考文献[5]中讨论了平面闭曲线的双切圆的存在性问题.他们的论文中,切割函数是一个重要的概念和工具.但是他们定义的切割函数仅适用于闭曲线.参考文献[6]将切割函数定义在一般的曲线上的,并讨论了切割函数恒为常值的曲线的形态.参考文献[7]考察了平面曲线的切割函数的分析性质.参考文献[8]的结果表明曲线的拓广的切割函数是一个运动不变量.本文将讨论曲线的切割函数与曲线的参数选择的关系.
1 相关概念
定义1.1 设r⇀(t)={x(t),y(t)}为平面曲线C 的一个正则参数化.κ(t)为其相对曲率.设r⇀(t0)是曲线上一点,称

为曲线的切割函数,

为曲线的拓广的切割函数,这里S={t|r⇀(t)=r⇀(t0).
例1.1 椭圆x(t)=a cos t,y(t)=b sin,a,b>0为平面正则曲线.t0为椭圆上任意一点的参数,则由定义1可知椭圆的切割函数为特别地,当a=b时,椭圆退化为圆.简单的计算可得圆的切割函数为f(t0,t)=1/a.这也验证了参考文献[6]的定理2.1.
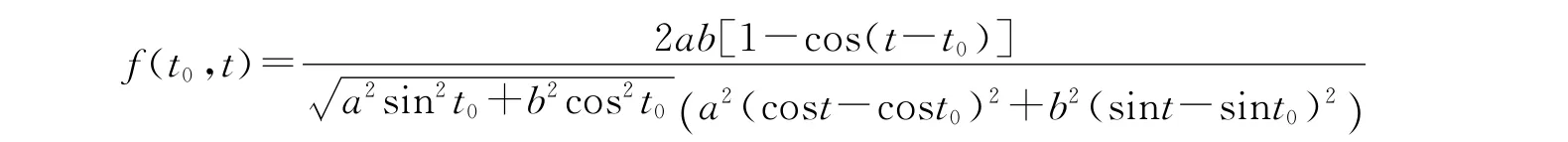
定义1.2 设r⇀(t)为空间曲线C 的一个正则参数化.κ(t)为其曲率.r⇀(t0)是曲线上一点.称
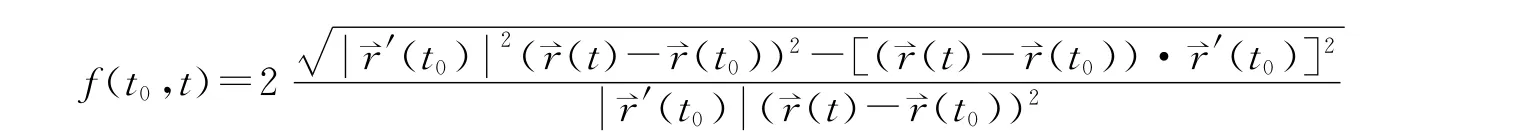
为曲线的切割函数,
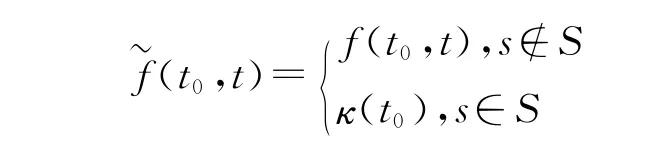
为曲线的拓广的切割函数,这里S= {t|r⇀(t)=r⇀(t0).
定义1.3[9]设r⇀(t)为曲线C的一个参数化.函数t=g)称为曲线C的一个参数变换,如果g′)存在、连续、且不为零.当g′)>0时,称t=g)是曲线r⇀(t)的保持定向的参数变换.
2 主要结果
定理2.1 定向平面曲线的拓广的切割函数与参数的选择无关.证明 设r⇀(t)={x(t),y(t)}为平面曲线C的一个正则参数化,
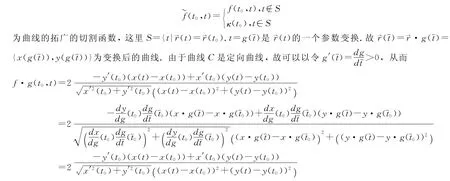
=f(t0,t)再考虑到定向曲线的曲率与参数的选择无关,定理立即可得.
定理2.2 空间曲线的拓广的切割函数与参数的选择无关.

为曲线的拓广的切割函数,这里S={t|r⇀(t)=r⇀(t0).t=g)是r⇀(t)的一个参数变换,r⇀)=r⇀·g
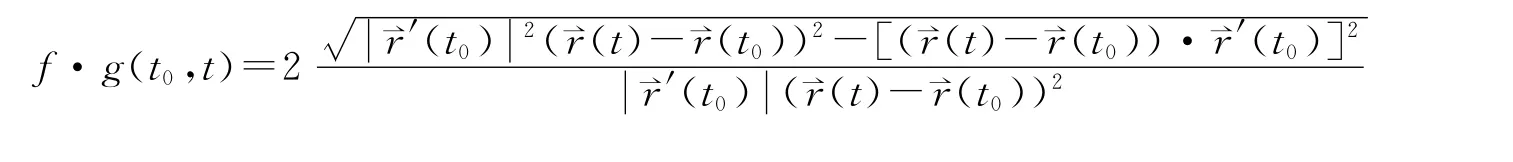
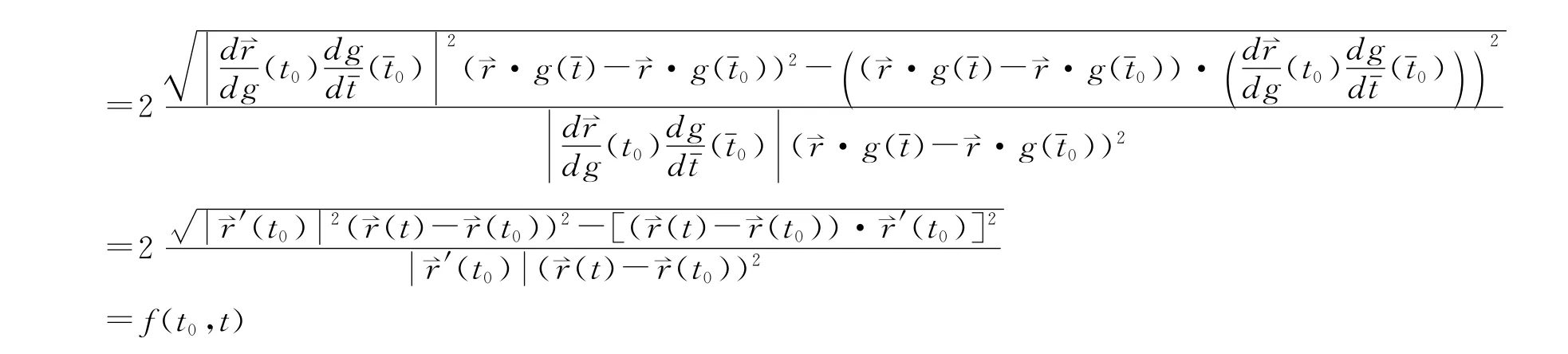
再考虑到空间曲线的曲率与参数的选择无关,定理立即可得.
定理2.1和定理2.2和参考文献[3]的结果立刻可以得到下面的定理.
定理2.3 平面定向正则曲线的切割函数是几何量;空间正则曲线的切割函数是几何量.
[1] Blum H.Biological shape and visual science [J].J Theoret Biol,1973,(38):205-287
[2] Brady M.Criteria for representations of shape[M].New York:Academic Press,1983:23-34
[3] Bruce M,Giblin PJ,Gibson CG.Symmetry set[J].Proc Royal Soc Edinburgh,1985,(101A):163-186
[4] Giblin PJ,Brassett SA.Local symmetry of plane curves[J].Amer Math Monthly,1985,(92):689-707
[5] Gibin PJ,O'shea DB.The Bitangent Sphere Problem [J].Amer Math Monthly,1990,97 (01):5-23
[6] 岳崇山,宋旭华.切割函数为常值的曲线的一个结果[J].河北北方学院学报:自然科学版,2010,26(03):13-15
[7] 岳崇山,宋旭华,景海斌.平面曲线的切割函数的分析性质 [J].河北北方学院学报:自然科学版,2010,26(04):14-16
[8] 岳崇山.切割函数的运动不变性 [J].河北北方学院学报:自然科学版,2010,26(05):10-13
[9] 陈维桓.微分几何 [M].北京:北京大学出版社,2006:25

