基于马尔科夫过程的大型机组三状态可靠性研究

唐玉玉

（重庆师范大学数学学院，重庆400047）

1 引 言

系统的可靠性是保证系统能够成功执行特殊任务的关键评价标准．对于大型机组系统的正常运行状况，评估此系统的可靠性显得尤为重要．然而，大多数可靠性文献研究的都是两个状态，即大型机组处于正常和停运两个状态组成的系统．在实际问题中，机组往往处于多种状态．例如 “一些大型发电机组经常处于部分停运状态，即机组不足100%地故障停运，而是可用发电容量只能达到额定容量的某1个值，即不能满载运行，称为降出力运行”［1］．本文针对当前国内大型机组系统降出力事故发生的实际情况，构建了以正常运行，停止运行及降出力运行为状态空间的三状态可靠性评价研究．这三种状态之间的转化是随机的，是一个典型的马尔科夫过程［2］，笔者利用连续参数马氏链的相关转移概率的结果，得到系统处于各种状态的概率，以及系统的可用度，从而为大型机组实际可靠性评价研究工作提供一定的帮助．

2 基于马尔科夫过程的大型机组三状态可靠性模型构建

2．1 大型机组系统可靠性定义

可靠性是指部件、零件、产品或系统在规定的环镜下、规定的时间内、规定条件下无故障地完成其规定功能的概率［3］．可靠性评定是利用产品的有限样本试验数据，考核和评价其可靠性指标的分析方法［4］．在一定的时间内，机组所处的状态都有发生故障的可靠性，且各种状态都是相互独立的，即机组从一个状态向另一个状态的转移不受其他时间段内状态转移的影响．

2．2 马尔科夫过程

马尔科夫过程是一类很重要的随机过程，这一类过程的特点是，当过程在时刻t0所处的状态已知，则过程在t0以后所处状态与过程在t0之前所处状态无关，这个特性叫无后效性也叫做马尔科夫性［2］，通俗地讲，就是 “已知现在，将来与过去无关”．马尔科夫过程应用非常广泛，它在近代物理学、生物学、公共服务事业、信息处理、自动控制、通信以及计算机等方面都有很重要的应用．

设 ｛X（t），t∈T｝为一随机过程，ti∈T，i＝1，2，…n，且t1＜t2＜…＜tn，如果对于状态空间S中的任意状态x1，x2…xn，X（tn）的条件分布函数满足：P｛X（tn）＜xn｜X（tn－1）＝xn－1…X（t1）＝x1｝＝P｛ X（tn）＜xn｜X（tn－1）＝xn－1｝，xn∈R则称｛X（t），t∈T｝具有马尔科夫性或无后效性，并称｛X（t），t∈T｝为马尔科夫过程，简称为马氏过程．称P｛ X（tn）＜xn｜X（tn－1）＝xn－1｝ 为马尔科夫过程的转移概率分布，称条件概率Pij（m，h）＝P｛ X（m＋h）＝j｜X（m）＝i｝，i，j∈I，m≥0，h＞0为｛X（n），n≥0｝的h步转移概率［5］．

2．3 模型构建

机组的运行结果可能出现以下三种状态：（1）满出力运行状态，即机组正常运行，（2）降出力运行状态．（3）不出力运行状态，即强迫停运［6］．在某一时刻，机组所处的状态为以上这3种状态中的一种，而在某个时间段中，机组所处的状态可能从其中的一种状态转移成为另一种状态．实际上机组的运行过程也是各类状态相互转化的过程，各状态在时间序列上服从指数分布，而且相互独立，tn时刻的状态只与时刻tn－1所处的状态有关，而与tn－1时刻之前的状态无关，因此，符合马尔科夫性，其三种状态即为马尔科夫链的三种状态［7］．满足条件存在且与i无关，这是马尔科夫过程的极限定理，又称为遍历性定理，即马氏链不论从哪种状态出发，当经过相当长的时间，达到j状态的概率都接近于πj，就是说，当机组运行相当长的一段时间后，机组所处三种状态的概率都将达到一个极限值，由此利用转移方程可求出机组处于各种状态的稳定概率，从而对可靠性作出较为准确的评价［8］．建立状态转移模型 （如图所示）

并作出如下假设：

（1）机组所处平稳状态概率矩阵为P（3），P（3）＝ P［P1，P2，P3］，P 为一步转移概率矩阵．

（2）从满出力运行状态到降出力运行状态的时间间隔序列T12服从指数分布，相应的分布函数为F12（t）＝1－e－λ1t，其中λ1为从状态1到状态2的故障率．

（3）从满出力运行状态到不出力运行状态的时间间隔序列T13服从指数分布，相应的分布函数为F13（t）＝1－e－λ2t，其中λ2为从状态1到状态3的故障率．

（4）从降出力运行状态到不出力运行状态的时间间隔序列T23服从指数分布，相应的分布函数为F23（t）＝1－e－λ3t，其中λ3为从状态2到状态3的故障率．

（5）从降出力运行状态到满出力运行状态的时间间隔序列T21服从指数分布，相应的分布函数为F21（t）＝1－e－μ1t，其中μ1为从状态2到状态1的维修率．

图1 状态转移模型

（6）从不出力运行状态到满出力运行状态的时间间隔序列T31服从指数分布，相应的分布函数为F31（t）＝1－e－μ2t，其中μ2为从状态3到状态1的维修率．

（7）从不出力运行状态到降出力运行状态的时间间隔序列T32服从指数分布，相应的分布函数为F32（t）＝1－e－μ3t，其中μ3为从状态3到状态1的维修率．

根据Chapman－Kolmogorov方程［9］，要求出机组处于各种状态的概率，则要满足以下条件：

再加上 （2）式全概率定理，即可得如下结果：

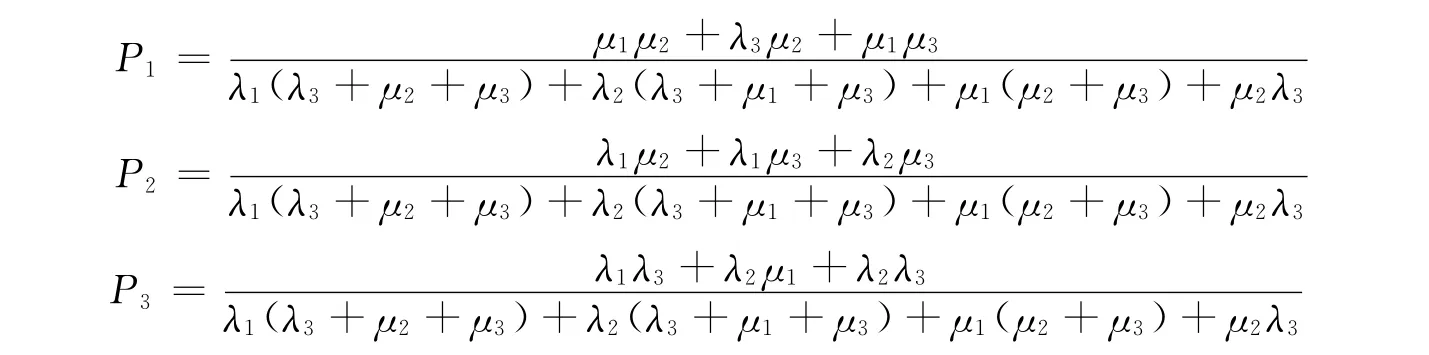
其中，P1为机组处于满出力运行状态的概率，P2为机组处于降出力运行状态的概率，P3为机组处于不出力运行状态的概率，系统在t时刻的可用度为A（t）＝P1＋P2．

3 结 论

本文从已有的可靠性理论找到切入点，首先，分析了大型机组系统的各种运行情况，提出了包括降出力运行状态的三状态研究模型，其次，利用马尔科夫过程的评价方法，计算出各种状态之中的转移概率以及处于每种状态的概率，并得出系统的可用度，能够在一定程度上对大型机组可靠性管理工作水平提供理论依据［10］．

［1］ 冯丽杰，姜洪波，刘卫星．大型发电机组三状态可靠性研究 ［J］．北华大学学报，2005，26（02）：35－36

［2］ 孙荣恒．随机过程及其应用 ［M］．北京：清华大学出版社，2004：24－27

［3］ 金星，洪延姬．系统可靠性与可用性分析方法 ［M］．北京：国防工业出版社，2007：150－155

［4］ 郭永基．可靠性工程原理 ［M］．北京：清华大学出版社，2002：235－258

［5］ 陆传赉．排队论 ［M］．北京：北京邮电学院出版社，2009：5－60

［6］ 周天宠，孟宪云，王守柱，等．两类三状态系统可靠度优化方法 ［J］．黑龙江大学学报．2009，28（03）：45－46

［7］ 唐应辉，唐小我．排队论基础与分析技术 ［M］．北京：科学出版社，2006：1－34

［8］ 孙荣恒，李建平．排队论基础 ［M］．北京：科学出版社，2002：20－69

［9］ 台文治，高世泽．一类具有可变输入率的排队模型 ［J］．重庆师范大学学报：自然科学版，2009，26（01）：245－247

［10］ 曹晋华，程侃．可靠性数学引论 ［M］．北京：科学出版社，2003：108－110