浅谈正态总体方差的假设检验与总体均值的联系
姚小娟,吕 陇
(兰州理工大学技术工程学院,甘肃 兰州730050)
对总体方差的显著性假设检验,是利用相应的检验统计量得出原假设的拒绝域,通过总体的样本,使用小概率事件的实际不可能性原则[1],最终作出拒绝或接受原假设的判断.当然,总体均值未知时与总体均值已知时,选择的检验统计量是不一样的[1],但有时会遇到总体均值未知时与总体均值已知时对原假设作出的判断是一样的,为什么会出现这种现象?又如何解释这种现象呢?
本文在样本容量固定的双侧及单侧显著性假设检验下,通过讨论总体均值未知时和已知时拒绝域之间的关系,对此种现象给出合理的解释.
1 有关正态总体方差的假设检验问题
对于单个正态总体的方差进行假设检验时,用χ2检验法[2].
已知总体X ~N(μ,σ2),σ2未知,X1,X2,Λ,Xn是来自总体X 的一组样本.要求检验假设:

如果总体均值μ未知,对总体方差的双侧假设检验的拒绝域记为:

2)总体均值μ已知的双侧假设检验中,由于样本二阶中心距M2是总体方差σ2的最小方差无偏估计,所以要选择样本二阶中心矩
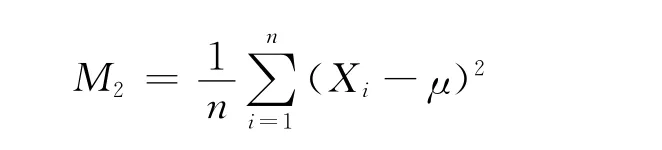
作为检验总体方差σ2的统计量.由样本观测值 (x1,x2,…,xn)算出的样本二阶中心矩M2的观测值为m2可类似地得到拒绝域:
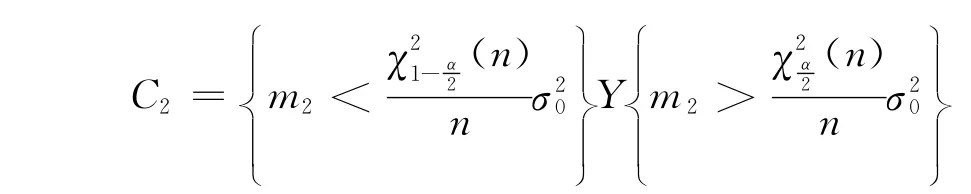
由样本观测值 (x1,x2,…,xn)算出的统计量m2的值,若它小于就拒绝原假设H0,否则就接受原假设H0.
在左侧假设检验:H0∶σ2≥σ;H1∶σ2<σ中,当μ未知时和μ已知时的拒绝域分别为C3,C4,则

在右侧假设检验:H0∶σ2≤σ;H1∶σ2>σ中,当μ未知时和μ已知时的拒绝域分别为C5,C6,则
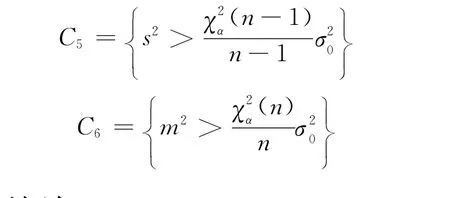
2 由两个不等式推导出的结论
2.1 总体均值μ未知与已知时拒绝域之间的关系
为了讨论总体均值μ未知和已知时拒绝域之间的关系,现将样本容量n固定,考虑显著性水平α.
参考χ2分布表并经过计算得[3]:
当α=0.005,0.01,0.05,0.10,0.25时,恒满足

当1-α=0.75,0.90,0.95,0.99,0.995时,恒满足

显著性水平α一般取值较小,依据小概率事件的实际不可能性原则[1],则由 (1)(2)这两个不等式,可得:

即,μ未知时的双侧假设检验下拒绝域C1包含在μ已知时的拒绝域C2内.
同理,由 (1)(2)这两个不等式可得,在单侧假设检验下有以下结论:
μ未知时的左侧假设检验下,则拒绝域C3包含在μ已知时的拒绝域C4内

μ未知时的右侧假设检验下,则拒绝域C5包含在μ已知时的拒绝域C6内

2.2 结 论
根据上述分析,总结得到以下结论:
在给定显著性水平α和样本容量n的条件下,单个正态总体方差的假设检验,在总体均值μ未知的情况下得到的拒绝域是包含在μ已知的拒绝域内.
由结论可知,若统计量的观测值s2、m2都落在μ未知时的拒绝域内,则必落在μ已知时的拒绝域内.此时,由μ未知时作出的对原假设的判断与μ已知时的判断是一致的.
反之,若统计量的观测值s2、m2都落在μ已知的接受域内,由显著性假设检验的接受域与拒绝域互补可知[2],s2、m2必落在μ未知的接受域内.此时,由μ未知时作出的对原假设的判断与μ已知时的判断是一致的.
2.3 例 子
下面就学生在平时练习中遇到的典型例子作具体分析:
例[4]机器包装砂糖,规定每袋糖的标准重量为500 g,均方差不得超过10 g,假设每袋糖的重量X~N(μ,σ2),现从包装好的各袋中随机地抽出9袋,测得净重 (g)507 497 510 475 484 488 524 491 515,问这时包装机工作是否正常 (α=0.05)?
如果视μ未知,那么通过样本观测值计算得:

由C5以及(n-1)=(8)=15.5得到拒绝域为:C5= (193.75,+∞)
可见s2落在拒绝域内C5,所以拒绝H0,即认为包装机工作不正常.
如果视μ已知,即μ=10,那么计算得检验统计量M2的观测值m2为:
通过分析注意到,本题中的总体均值无论视为未知还是已知,对原假设作出的判断是没有影响的,都拒绝了原假设,为什么会出现这种现象呢?根据本文得到的结论可知,这是由于若检验统计量S2和M2的观测值s2、m2都落在μ未知时的拒绝域内,此时无论总体均值μ未知还是已知,对原假设作出的判断是一致的.
[1] 沈恒范.概率论与数理统计教程 (第四版)[M].北京:高等教育出版社,2006:1-30
[2] 陈希孺.概率与数理统计 [M].合肥:中国科学技术大学出版社,2004:20-65
[3] 盛骤,谢式千,潘承毅.概率与数理统计 (第三版)[M].北京:高等教育出版社,2001:30-77
[4] 陈魁.概率统计辅导 [M].北京:清华大学出版社,2004:9-60

