电话网话务量周期性建模与分析
王 涛,张志明
(1.中国联合网络通信集团有限公司广东省分公司运行维护部,广东广州 510663;2.郑州牧业工程高等专科学校信息工程系,河南 郑州 450011)
对于交换机来说,输入的是电话呼叫,且呼叫时间是不确定的一些随机事件.话务理论就是描述这种随机事件的特性、规律以及它们与交换机的数量和服务质量关系的理论.
电话业务量简称话务量.业务量是指在指定时间内线路被占用的总时间.话务量为单位时间内发生的呼叫数a与每次呼叫平均占用时长t0的乘积,用A表示,则话务量A=at0.
1 时间序列分析
1.1ARMA 模型
时间序列由相应的随机过程产生.按时间次序排列的随机变量序列称为时间序列X1,X2,…,如果用 x1,x2,…,xN分别表示随机变量 X1,X2,…,XN的观察值,就称 x1,x2,…,xN是时间序列 X1,X2,…,XN的N个观测样本,其中N是观测样本的个数.
ARMA模型(Auto Regression Moving Average)称为自回归移动平均模型,分为AR模型、MA模型和 ARMA 模型[1].
定义1 具有式(1)结构的模型称为p阶自回归模型,记为AR(p):
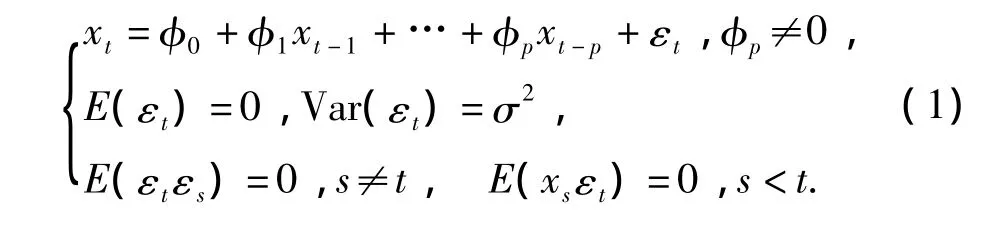
定义2 具有式(2)结构的模型称为q阶移动平均模型,记为MA(q):
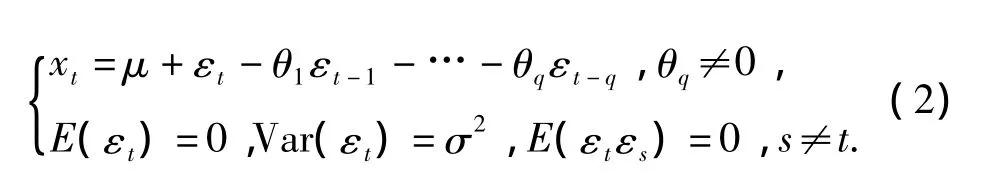
定义3 具有式(3)结构的模型称为自回归移动平均模型,记为ARMA(p,q):
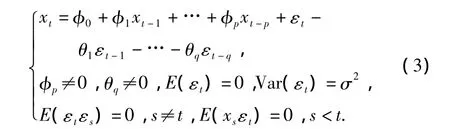
1.2 潜周期模型
任何时间序列经过合理函数变换后都可以被认为由3部分叠加而成,即趋势项部分、周期项部分和随机噪声项部分.对于话务量这种具有明显周期性的时间序列,可以用潜周期模型进行建模.
在信号处理领域,余弦波信号是一种常见信号,在随机干扰背景下能否成功检测出各信号的角频率成分及其振幅是信号处理的关键.通常余弦波信号用潜周期模型来描述
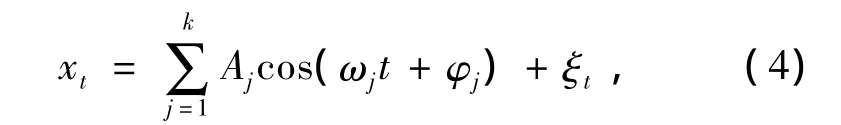
式中:0<ω1<ω2<… <ωk≤π;正数Aj为角频率ωj的振幅,ωj< 0;φj为初始相位,φj∈[0,2π);ξt为干扰项.
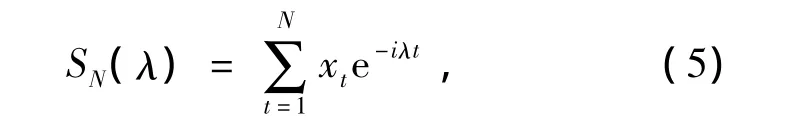
在设参数估计前,先对数据进行零均值化处理.设处理后的数据为 x1,x2,…,xN,引入函数当N充分大时,实值连续函数SN(λ)在区间[0,π]上的图形有若干个峰群,峰群的个数就是潜周期模型中的周期(或角频率)的个数.根据角频率的估计量定义αj的估计为

b.构造 SN(λ),通过 SN(λ)估计 ωj;
c.计算各角频率对应的αj;
d.计算振幅Aj和初始相位φj;
e.计算残差ξt及其样本自协方差函数 γk,k=1,2,…,N,如果γk有收敛到零的性质,就可以认为模型合适,如果不是,可以对ξt建立AR或ARMA模型,构造混合AR潜周期模型,或者混合ARMA潜周期模型,同时对模型进行检测.
文献[2]利用了潜周期模型对网站访问量进行了建模,取得较好效果.
1.3 季节效应分析
呈现出固定周期性变化的事件,称为具有季节效应.季节效应使得时间序列呈现出相似性.
为了得到数量化的季节信息,给出季节指数的概念.所谓季节指数,就是用简单平均法计算的周期内各时期季节性影响的相对数.季节指数的计算分
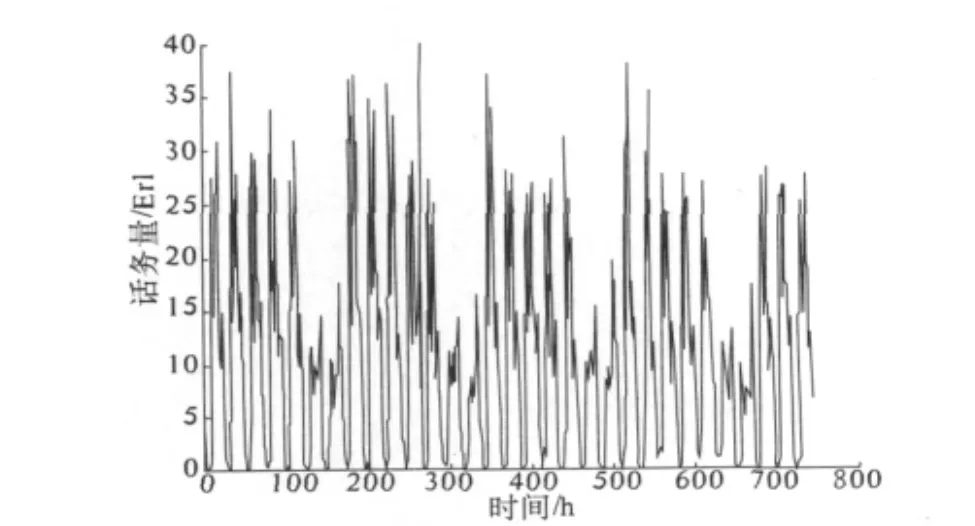
图1 交换机A到节点B话务量
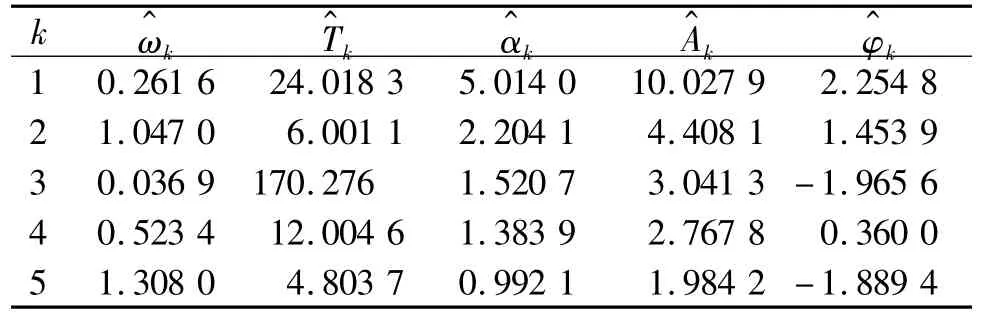
表1 话务量模型估计参数
由公式(5)忽略ξt构建模型为3步.
第1步:计算周期内各期平均数,得到长期以来该时间的平均水平.假定序列的数据结构以m为周期,共有n周期,则
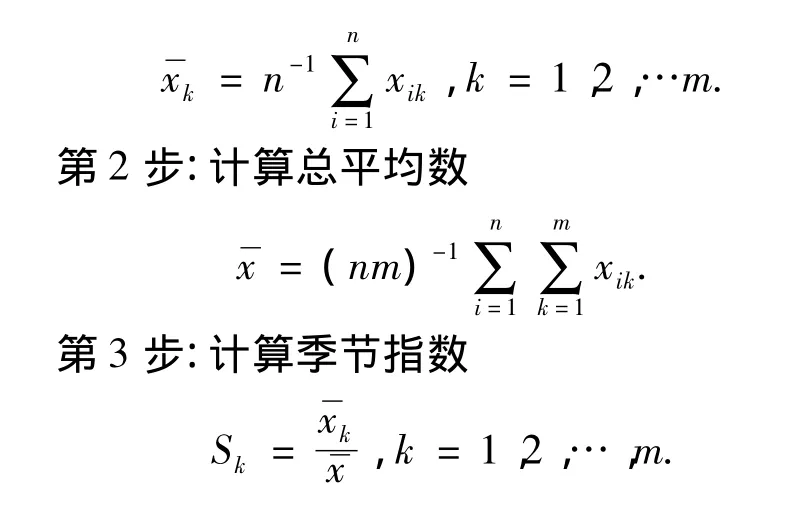
季节指数反映了该季度与总平均值之间的一种比较稳定的关系.如果这个比值大于1,说明该季度的值常常高于总平均值;如果这个比值小于1,说明该季度的值常常低于总平均值;如果比值近似等于1,说明该序列没有明显的季节效应.
2 话务量的周期性模型仿真与分析
笔者利用上述方法,对话务量建立潜周期模型,并采用季节指数对话务量进行季节效应分析.
以交换机A到节点B话务量为例,如图1所示,时间单位为h,取1个月共744 h的数据.话务量平均值为10.772 2 Erl.利用最小二乘法分析其趋势为0,对数据进行0均值化,利用公式(5)绘出图2,图2得到话务量的5峰群结果见表1,可见话务量的周期有 24,6,170(约合1 周),12,5 h.
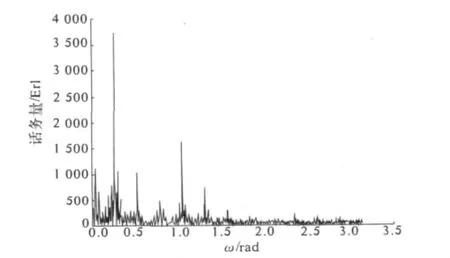
图2话务量SN(λ)周期变化图

把模型(7)与实际值对比,得到图3.
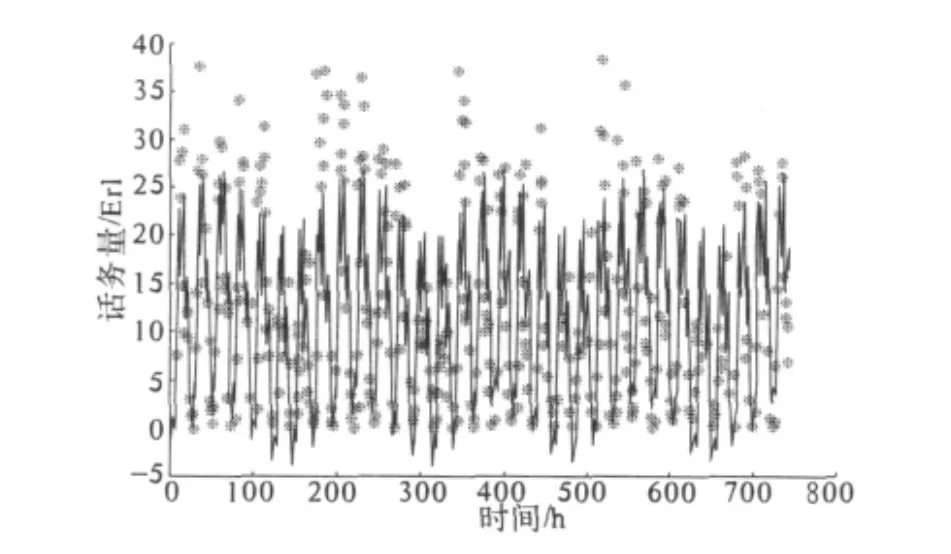
图3 模型(7)与实际值对比
其中*号为实际值.可见预测值与实际值仍有一些差异,因此对ξt建立AR模型得到最终模型为混合AR潜周期模型
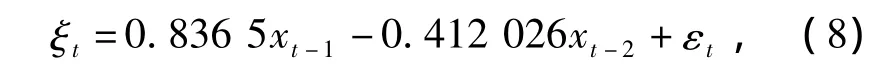

用模型(9)与实际值对比得到图4.
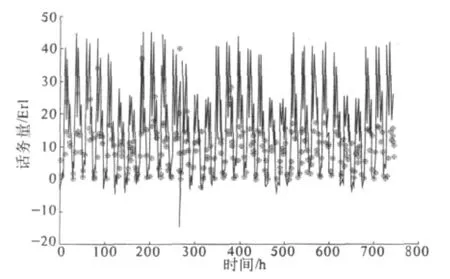
图4 模型(9)与实际值对比
通过分析图4的残差,拟合效果较好.从潜周期模型知其主要周期为24 h,对话务量进行24 h的季节性效应分析,得到季节指数图,如图5所示.

图5 话务量季节指数图
由图5可知,交换机A到B节点方向的话务量,1 d内最忙时是10:00和15:00,这与大众印象中的10:00和20:00有出入.通过对不同交换机到不同方向的话务量进行季节指数分析,得到不同方向的忙时不一样,这种差异性为网络的优化提供了条件.
3 结语
采用一种混合潜周期方法对电话网话务量同期性进行建模.仿真结果显示模型对实际数据的拟合效果较好,对电话网络的优化有一定的帮助.
[1] Box G E P,Jenkins G M,Reinsel G C.Time Series Analysis:Forecasting and Control[M].Upper Saddle River:Prentice Hall/Pearson,1994.
[2]王继民,彭波.搜索引擎用户访问量模型[J].计算机工程与应用,2004(25):9-11.
- 华北水利水电大学学报(自然科学版)的其它文章
- CFRP和角钢复合加固损伤混凝土柱的承载力计算

