几种动点轨迹形成的动态演示

于晓晶

(苏州市职业大学 教育与人文科学系，江苏 苏州 215104)

动点的轨迹问题是解析几何的一个核心问题，有些动点的轨迹方程易求，但很难想象其形状、位置等特征，而描绘动点轨迹的形成过程是传统教学手段无法实现的。将Matlab软件引入到解析几何教学研究中，则可弥补传统教学的不足，是解析几何教学的一个有力辅助工具。使用Matlab强大的图形设计功能，就可以轻松得到动点轨迹形成的图形，而且可以直观、动态地研究动点轨迹形成的过程及其特征，从而激发学习兴趣，促进探究学习，提高教学效率。

本文以摆线、外旋轮线、渐伸线、圆柱螺旋线、圆锥螺旋线为例，给出动点轨迹形成的演示过程的Matlab程序代码。

1 摆线

一个半径为a的圆在一直线上无滑动地滚动，圆周上点P的轨迹由一系列完全相同的拱形组成，这种曲线叫做旋轮线或称为摆线。

适当选取坐标系，可写出P点的参数方程

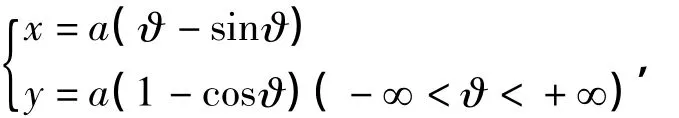
不妨取a=1，利用Matlab软件编制以下程序代码，则可演示摆线的形成过程如图1:

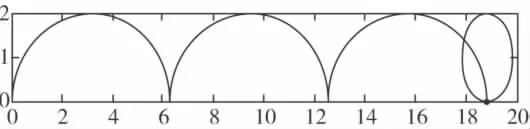
图1 摆线

2 外旋轮线

当一圆沿着一个定圆的外部作无滑动地滚动时，动圆上一点P的轨迹叫做外旋轮线，我们用a和b分别表示定圆与动圆的半径。其参数方程为

图2 外旋轮线

将程序中外旋轮线参数方程改为内旋轮线参数方程

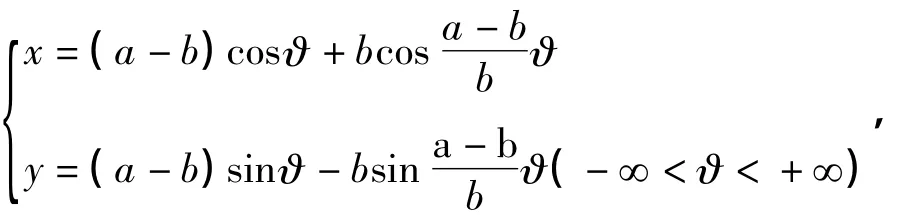
则可演示内旋轮线的形成过程(图3a为a=4，b=1;图(3)b为a=5，b=1;图(3)c为a=8，b=1)。

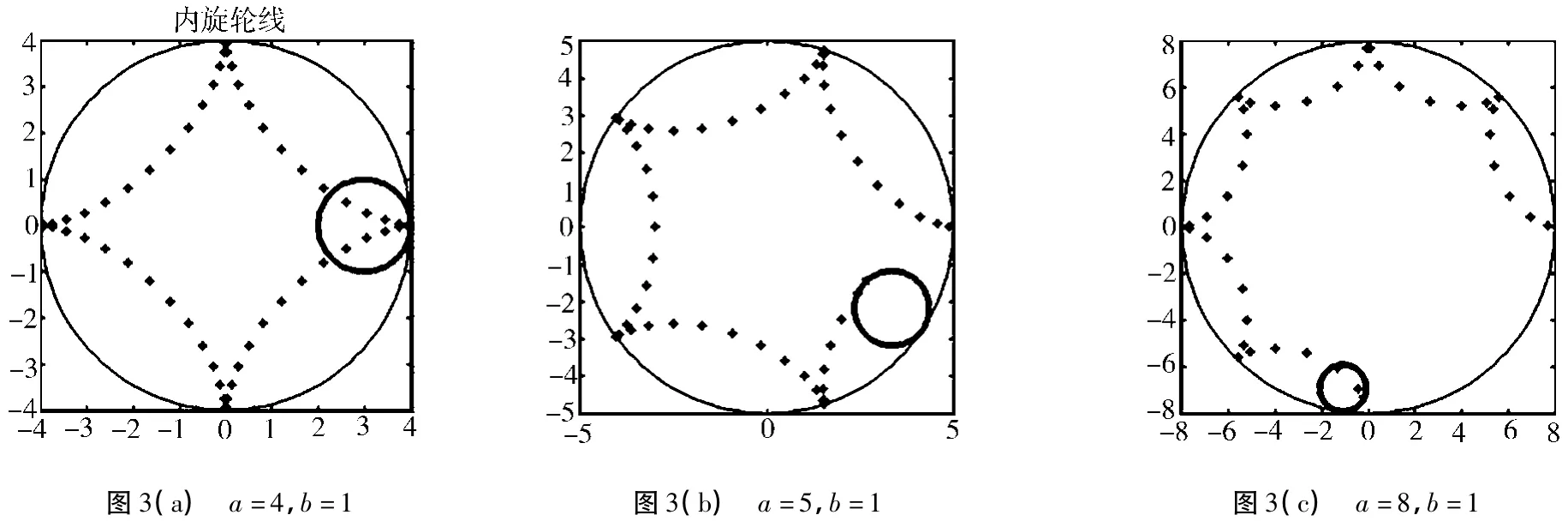
图3 内旋轮线

3 渐开线

把线绕在一个固定圆周上，将线头P拉紧后反方向旋转，以把线从圆周上解放出来，使放出来的部分分成为圆的切线，则线头P的轨迹为圆的渐开线或切展线，工业上被采用为齿廓曲线。其参数方程为

选取a值及参数范围，利用Matlab软件编制以下程序代码，则可演示渐开线的形成过程(见图4)。

图4 圆的渐开线

4 圆柱螺旋线

一个质点一方面绕一条轴线作等角速度的圆周运动，另一方面作平行于轴线的等速直线运动，其速度与角速度成正比，求这个质点运动的轨迹方程。

解:通过计算易求得该曲线的参数方程为

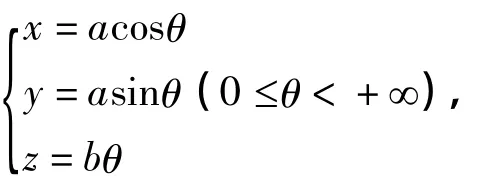
其中θ为参数，曲线的形状像弹簧，通常叫做圆柱螺旋线。

图5 圆柱螺旋线

利用Matlab三维彗星图函数的作图功能，可以让学生直观地看到轨迹的形成过程演示。图5中是已经形成的静态轨迹，输入下列程序代码可以看到轨迹动态形成过程。

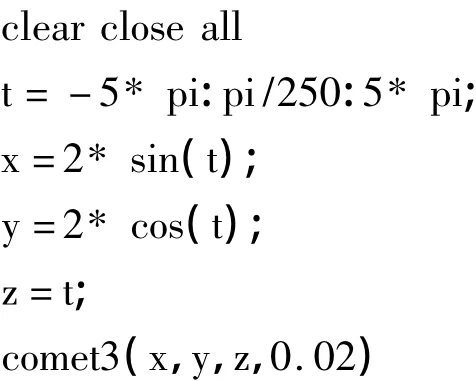
5 圆锥螺旋线

有一质点，沿着已知圆锥面的一条母线自圆锥的顶点起，作等速直线运动，另一方面这一条母线在圆锥面上，过圆锥的顶点绕圆锥的轴(旋转轴)作等速的转动，这时质点在圆锥面上的轨迹叫做圆锥螺线，试建立圆锥螺线的方程。

解:通过计算易求得该曲线的参数方程为

其中α为圆锥半顶角，ω为角速度，v为直线速度。

此轨迹也利用Matlab三维彗星图函数的作图功能，可以让学生直观地看到轨迹的形成过程演示。如图6所示。

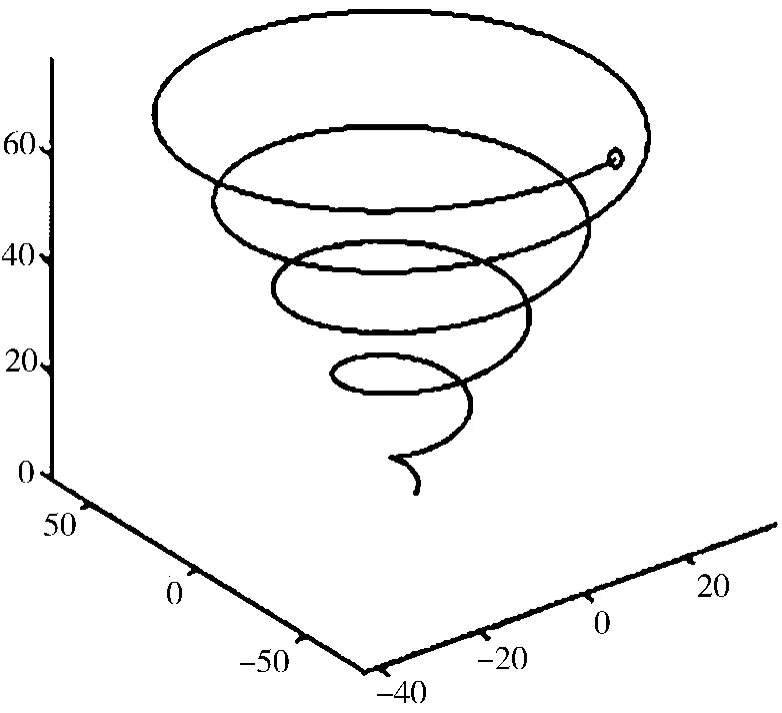
图6 圆锥螺旋线

函数comet3显示的是非常生动的彗星图，其中一个圆形(彗星头部)显示在屏幕上。彗星的主要部分是一个紧随头部的拖曳部分。尾部则是一条包含整个函数的实线。但是其留下的痕迹是使用None的Erase-Mode创建的，不能打印或使用Redrew编辑，否则痕迹将消失。

利用Matlab编程如下，可以见图7。

图7中是已经形成的静态轨迹，输入下列程序代码，可以让学生直观地看到轨迹的形成演示过程，而且可以旋转图形，从不同角度观察、研究轨迹的形状特征。

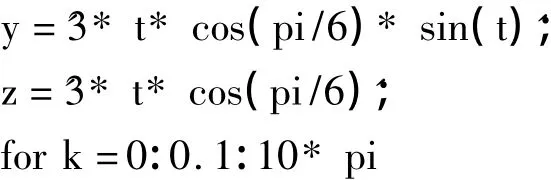
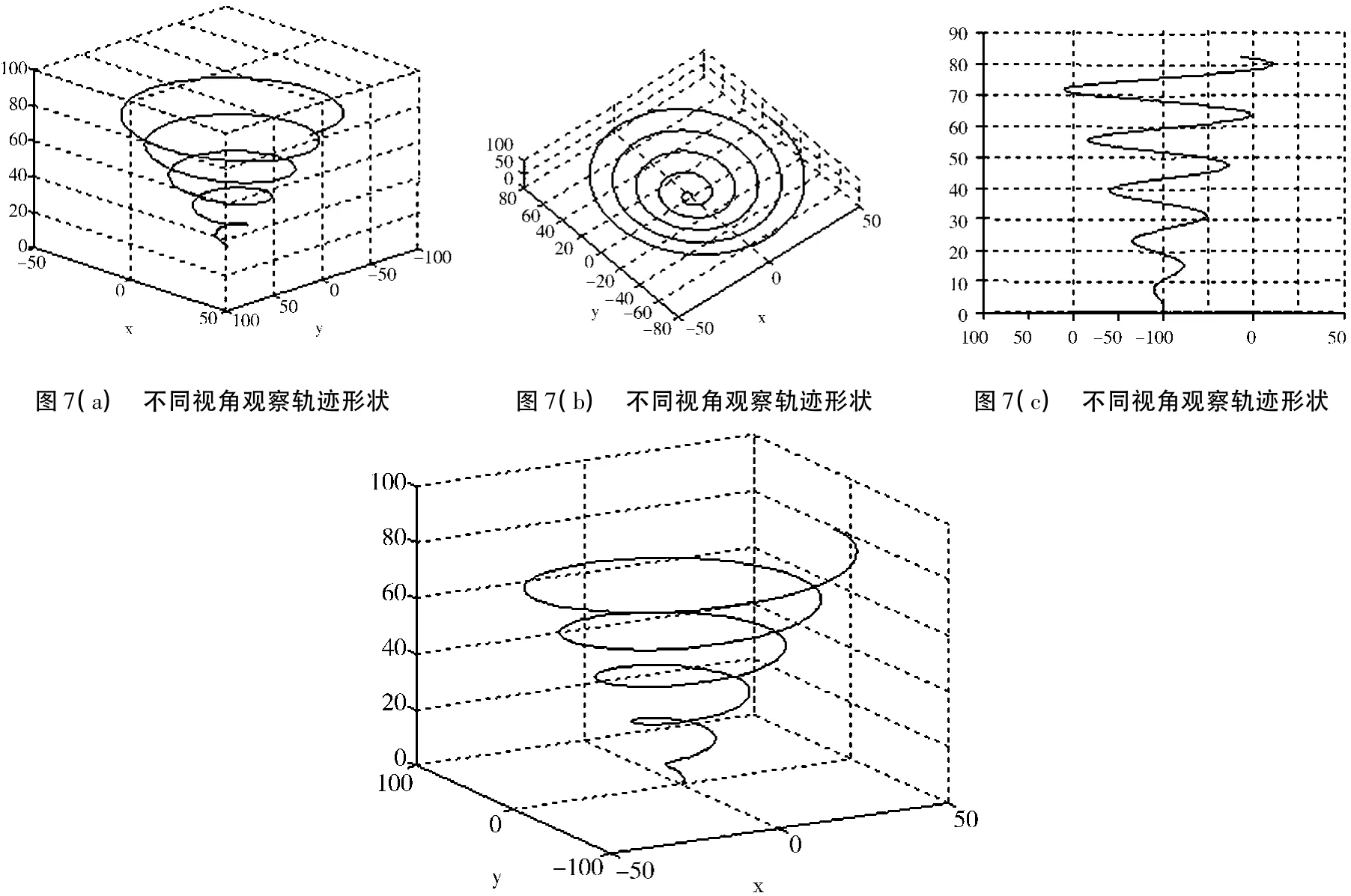
图7 圆锥螺旋线

图7(a)、图7(b)、图7(c)是从不同视角观察的轨迹形状。

［1］于晓晶.Matlab在解析几何教学中的应用［J］.电脑知识与技术，2009(10):8219－8221.

［2］赵亚男，牛言涛.MATLAB在解析几何教学中的应用［J］.长春大学学报，2011(4):54－58.

［3］于坚.MATLAB软件在解析几何教学中的应用［J］.广西教育学院学报，2006(1):16－20.

［4］张宏民.Matlab在解析几何教学中的应用［J］.高师理科学刊，2007(3):87－89.

［5］任明慧.Matlab在空间图形中的动态应用［J］.数学理论与应用，2008(3):40－44.