筛板塔的设计和计算软件的应用
齐福来
(中国石化集团上海工程有限公司,上海 200120)
1 综述
在工业上最早用于蒸馏分离的设备是泡罩塔,随后在十九世纪出现了在板上穿孔使气液在板上进行热质交换。穿孔的板式塔可带降液管,也可不带,不带降液管的穿孔板塔在工程上给它取了个名字叫‘穿流板’,带降液管的就叫‘筛板塔’。穿流板的操作给板式塔带来新的概念,由于气-液除在板上的气液热-质交换外,在孔内气液之间激烈接触仍进行着热-质的交换,因此,在传热-传质效率方面具有优势。但由于操作的稳定性问题,现在广泛使用的仍是筛板塔。
筛板塔是所有板式塔中造价最便宜的一种塔型,它的制造较简单,操作稳定,可以适用于较污浊和有悬浮颗粒的物料。板上的孔径为3~13 mm,开孔面积6~10%。也有采用较大孔径(10~25 mm)的情况,因为,大孔径不易堵塞、通量大、压降低,当设计合理时同样可以得到满意的效果。国内也做过研究[1],但是由于漏液点的气速要求较高,所以,板的操作范围就较狭窄,不易掌握,只有在较稳定的生产情况才可采用。从效率和容量上来看,当在筛板塔的设计范围操作时,其效率优于泡罩塔,效率提高15%,其生产能力增加10~15%[2],然而在某些装置其容量可以是泡罩塔的1.5~3倍[3]。在筛板塔的开发初期由于对其性能的不了解使用的不多。后来由于渐渐地研究,由上个世纪40年代起研究者发表了不少的文章,也由此筛板塔被人们真正的了解且大量使用。由于发表的文章太多,现将在这方面的研究文献,选择性的分类予以介绍,读者可以去参考。
在筛板塔的研究上着重于几个方面:
1.1 筛板上的开孔及压降
筛板塔的干板压降与开孔大小、与板厚的关系以及开孔率的关系[4~8,12];液流的大小对压降的影响[4,5,9,10];流体在板上的梯度[4,6]。
1.2 设计计算
Fair[12]1963年对筛板塔的设计给出了全面的建议,Eduljee[17]列出了计算的全过程,对三种计算方法进行了比较,并且从经济角度进行了考虑。
Kister[38]对于应用于蒸馏方面的筛板塔也做了全面的介绍,加上他是FRI研究机构的人员,因此,实用性比较强。
全面介绍用计算机计算筛板塔的是希腊社会服务部的Economopoulos 博士于1978年发表的文章[11]。
1.3 在设计程序软件方面较有名的是FRI
(Fractionation Research Inc.)它具有自己的私有权的研究结果,具有会员资格的机构才可使用。
本人根据发表文章的收集和计算研究,编制了计算筛板塔的软件‘SieveTray’。

在没有条件使用FRI等专利软件且无机会去深入研究的设计人员以及厂方的设备设计人员作为基础的研究计算之用。也可供大学生作为条件设计实验之用。
以下就一些编制软件的基本公式和设计筛板塔的关键参数作一介绍。
2 筛板塔的操作特性
Anorld 等人[9]根据典型的筛板塔对不同的气速和液量试验标绘出了压力降与气速的关系图1。
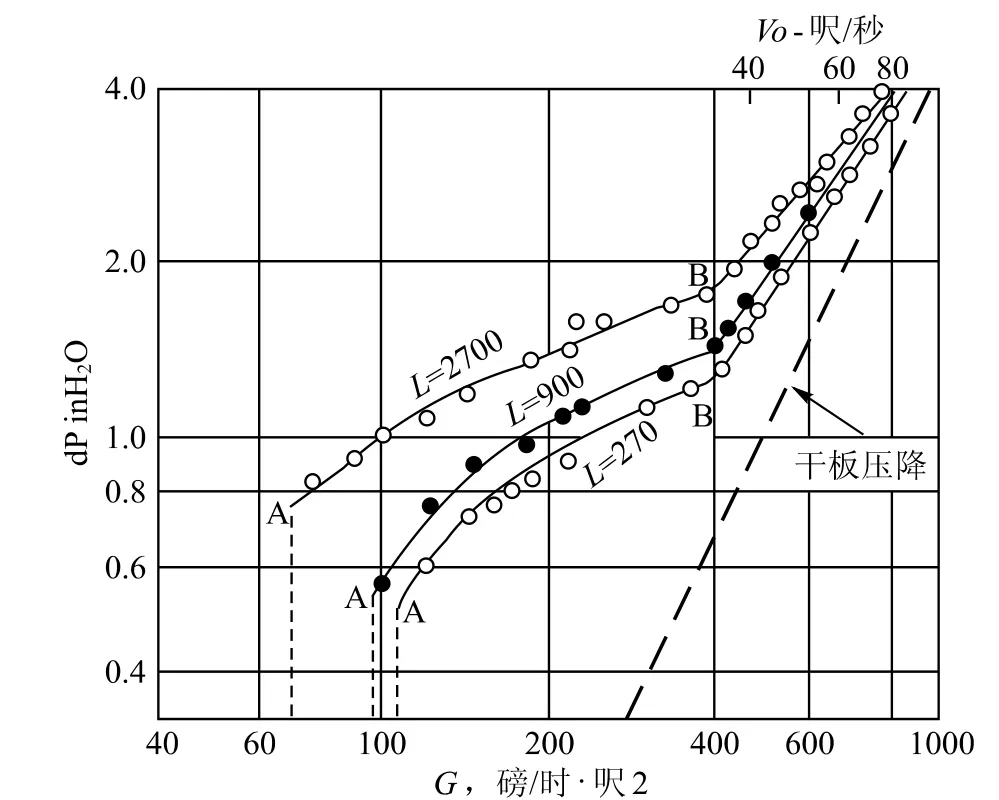
图1 6.5 mm的孔 孔面积为4.5% 试验系统为水-空气堰高12.5 mm G ,L的速度均以全塔面积计算Vo -孔内的气速
图1的竖坐标为塔板的压力降dP,单位,inH2O;横坐标为空塔气速,磅/小时·呎2。在塔正常操作时气体由孔中流过的速度应该阻止板上的液体由孔中向下流动,不然就很难保证塔板上的液位,这也就是筛板塔操作的最小气速,称为‘载点’(Seal point),也就是图1中的A点。由图1看出:不同的液流量其载点也不同。由于液量的变化影响到在板上清液的高度,同样,溢流堰的高度也影响到载点气速。
气速的增加压降也将增加,在孔中的漏液量继续减少,到B点时基本上不漏液了,这点也称为‘泪点’(weep Point)。B点以后全塔的孔达到稳定的鼓泡状态,再继续增加气速,塔板压降急速升高,这时塔板将进入可能液泛的状态。而筛板塔板的操作应该在泪点B以上和液泛点之间的范围。
因此,Eduljee[17]将泪点的气速作为最小气速来计算塔径。他[19]以下式来计算泪点的气速:
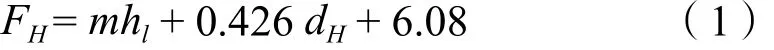
式中:m和孔径的关系如表1。

表1 m值与孔径的关系表
筛板塔的操作上限,即液泛点(Flooding point),液泛产生的原因有两个方面,一个是由于塔板的压力降加大使降液管产生反冲阻止液体的下流,另一个是气速的加大产生大量的雾沫夹带气液平衡遭到破坏。Fair[20]建立了下图关联板间距,孔面积和表面张力对液泛气速的影响图:
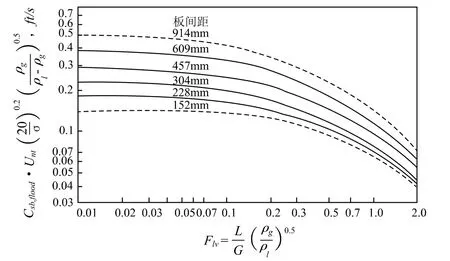
图2 Fair & Mathews 对于筛板塔的液泛曲线图
图2的横坐标中的L/G项为重量比。竖坐标的单位为英制,转换成SI制时乘以0.3048即为下式:
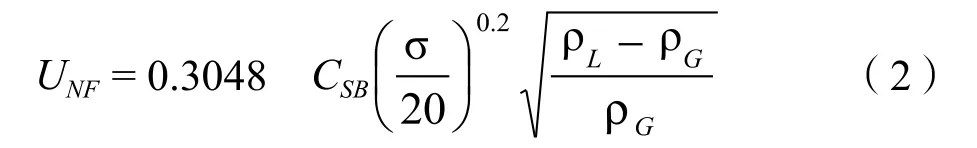
气速UNF是基于气体通过的有效面积,即为全塔面积减去降液管面积AN=AT- Ad。
1986年Lygeros & Magoulas[21]建立了计算图2的关系式Csbf= 0.3048 Csb:
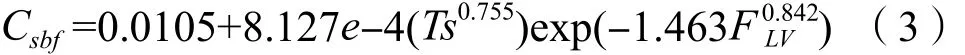
Eduljee以最小气速来估计塔径,而fair以最大液泛速度的百分数来估计塔径。区别在于前者以保证筛板塔能正常地运转,后者的目的是保证筛板塔处于高效的操作。1982年美国化工协会(AIChE)发表了FRI的两个数据和在Oldershaw实验塔中得到的筛板塔板的液泛百分数与Murphree板效率或者总效率的关系图3[22]:
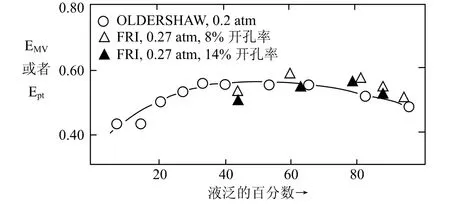
图3 1 英寸的Oldershaw 塔总效率和4 英尺直径的FRI 塔的Murphree 板效率与液泛百分数的关系图
从图3看出,随着液泛百分数的增加塔板效率呈一曲线,过低或过高的液泛百分率效率都会降低。过低气速使气体和液体的混合效率降低效率也就降低,过高气速时产生了过多的雾沫夹带,产生了过多的反混使塔板效率降低。所以,选择适当的液泛百分率的气速来设计塔径将会使塔的操作更有效。一般选择60~80%。
3 筛板塔的版面布置
筛板塔的板面总布置以及参数的选择:
对于单流程的带有弓形降液管的筛板塔的版面布置如下图4:
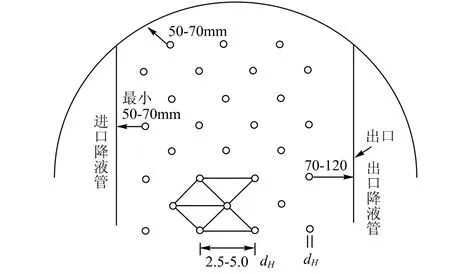
图4 筛板塔的筛孔布置,孔与进口降液管、出口降液管以及孔之间的建议距离图
孔与孔之间的距离既要使板上的液体充分混合又要互不干扰太多。B.H.C 研究了孔之间不影响的距离见表2。
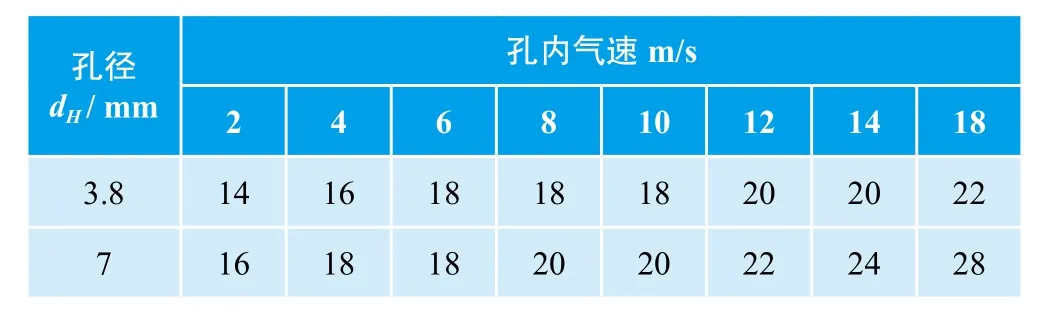
表2 孔之间的不干扰距离和孔径、气速的关系表
由表2看出在不同气速时互不干扰的距离不同,一般在2.5 ~ 5.0 dH之间。孔间距根据不同的生产条件可以任意选择,不过最一般的选择是在3.5 dH的距离。
筛孔与进口降液管的距离称为分配区,目的是使进入的液体均匀的分配到全塔板,这个区域的宽度一般选择50~70 mm。
筛孔与出口降液管堰的距离称为安定区,目的是使进入降液管的液体少含气体泡沫,这个区域的宽度一般选择70~120 mm。
筛孔与塔壁之间的距离称为支撑环区,它的宽度一般取50~70 mm。
4 筛板塔板的设计计算
筛板塔的设计计算包括:塔径计算,塔板压降计算,雾沫夹带,液泛的计算,筛板塔板的效率计算,现分项予以叙述:
4.1 塔径的计算
在决定塔径时可以根据塔的允许气速,就像前面所介绍的,也可以根据所需要的塔的面积来计算。全塔的面积可分为两个部分,一个是塔板上气液进行质交换的面积,被称为有效面积,另一个是降液管占据的面积。全塔的面积如下式:

再由AT求得塔径。
4.1.1 塔板的有效面积Aa
塔板的有效面积就是布置筛孔的板面部分,在该部分气液进行热-质的交换,既是决定板效率也是决定气体通量的关键。
关于这部分的面积计算Glitsch 公司手册[23]推荐:
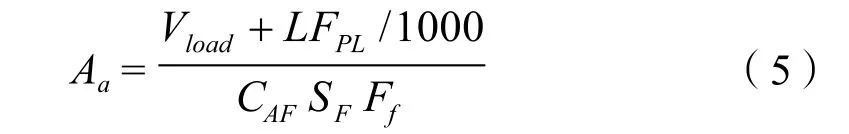
式中:
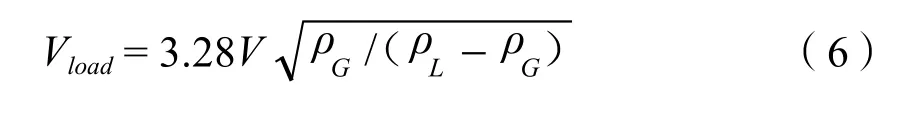
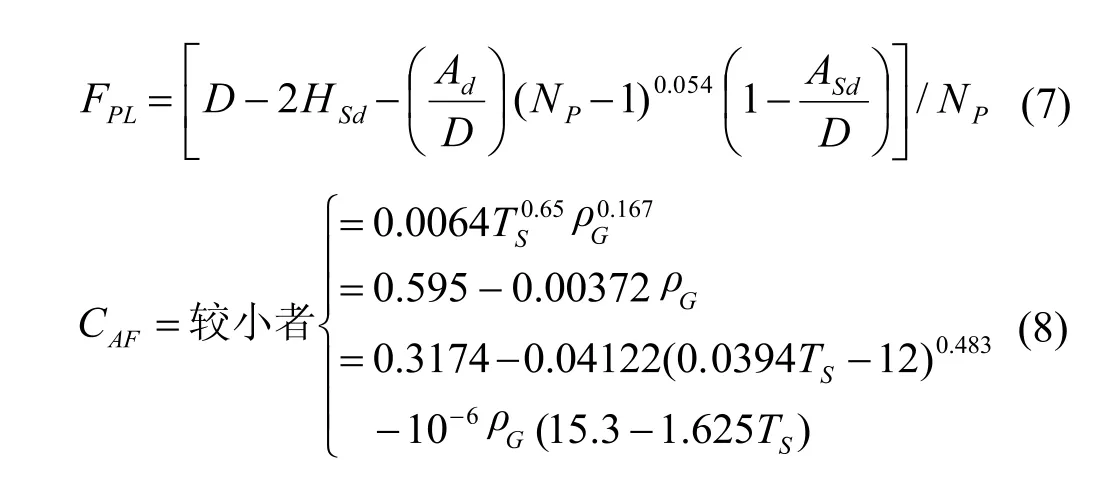
SF为系统特性参数,取值与系统的泡沫特性有关,按表3选取:
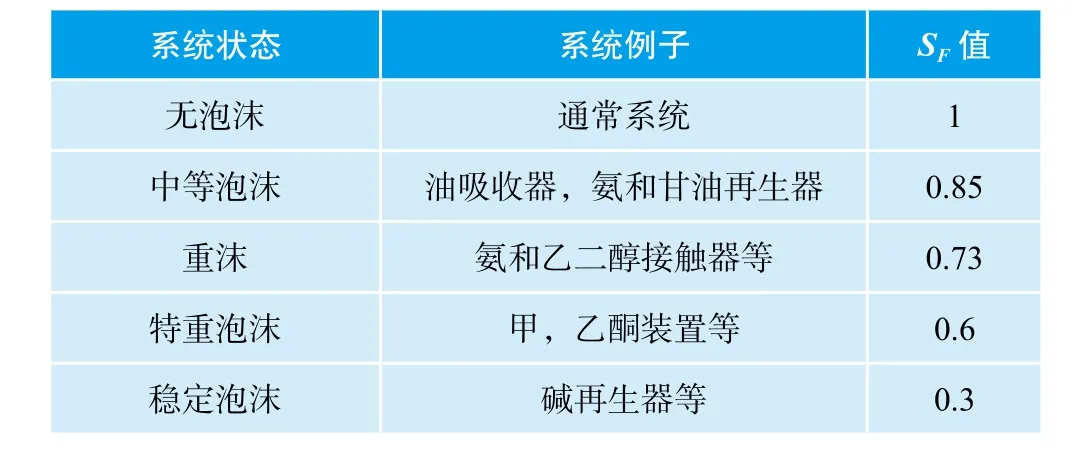
表3 系统特性参数表
Ff—塔板的液泛因子,为液泛的百分率。
Glitsch 建议常压操作时取Ff= 0.82;减压操作时取
Ff= 0.77。
Koch 公司手册[24]推荐:
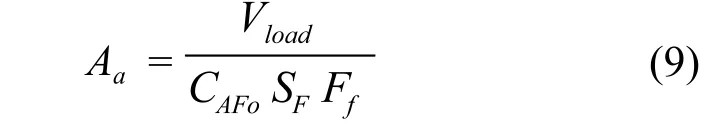
式(9)中的CAFo按下式决定:
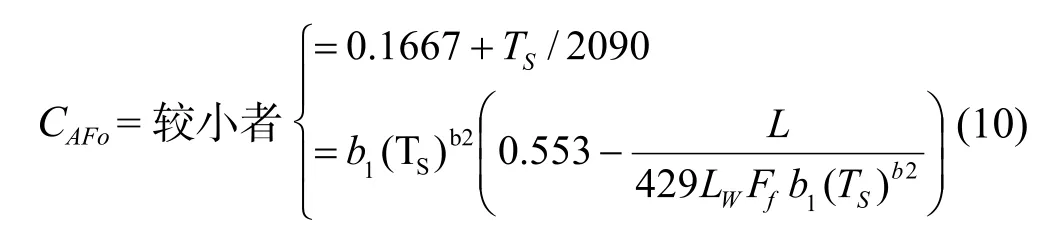
式(10)中:
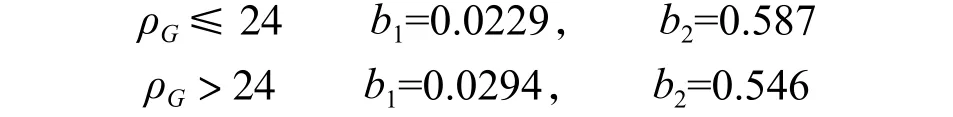
Ff和SF取值与式(5)相同。
Fair[12]采用式(9),但以FLV代替Vload。
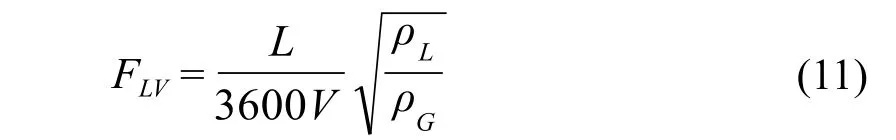
Fair采用的容量系数CAFo为:
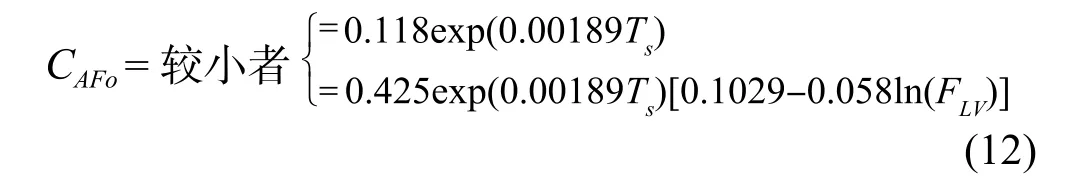
Fair的SF取值与系统的表面张力有关:

Fair的计算方法比较保守。
4.1.2 降液管面积Ad
单流程时一般采取弓形降液管,其降液管的面积和液流堰长度的决定按如下的规定:
液流堰长度一般取塔径的60~75%。
还有一个决定降液管面积的经验方法:就是按其允许的液流量或者说是允许的液体在降液管中的流动速度限制来决定降液管所需的面积。一般降液管的允许流量为:200 ~ 250 m3/h·m2。
弓形降液管面积与塔面积的比例和弓形降液管堰长与塔径的比例关系可由下式计算:
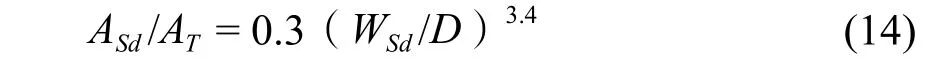
该公式在0.45 <(WSd/D)< 0.85范围时其误差在+2%和- 4%之间。
当知道弓型降液管的弦高HSd则可由下式计算ASd/AT的值:
令B=HSd/ D;
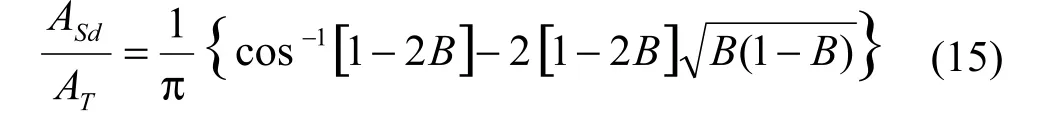
当知道弓形降液管的弦高HSd时也可计算塔侧弓型降液管的堰长WSd:
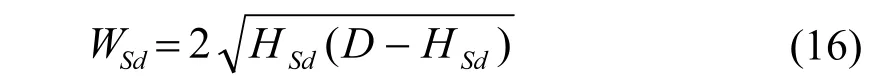
Glitsch公司手册[23]推荐的降液管的面积:

式中:A′d= 4.4 L / VdFf
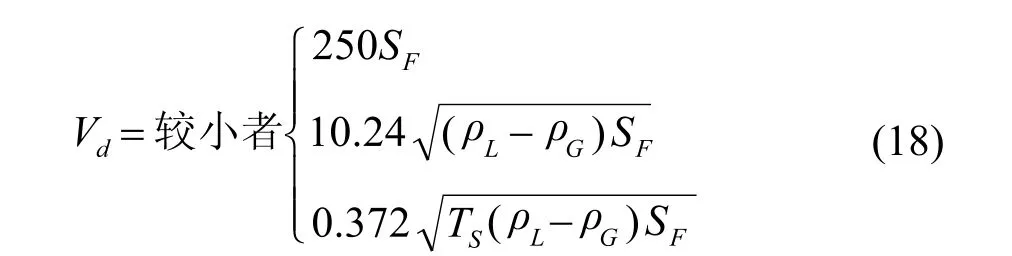
Koch 公司的手册[24]推荐的降液管面积:
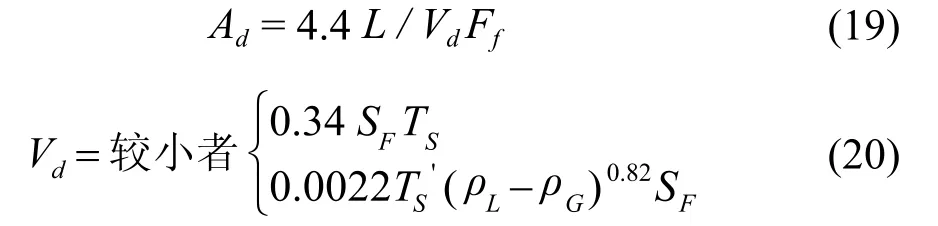
T ′S= TS和762的较小值
4.1.3 筛板塔板上的流程数以及流路的长度和宽度的计算
筛板塔板上的流程数目和其他板式塔一样与液体负荷有关,本部分内容可参阅文献[2]pp110。也可参考文献[18]。对于多流程的塔板,知道总的降液管面积Ad也知道塔板上流程的数目NP,就可以求得塔侧降液管的面积:
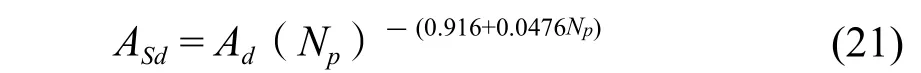
在板上的最大流程数目可由下式计算:
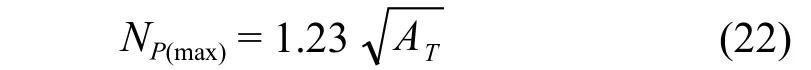
多流程时筛板上的总堰长可由下式计算:

多流程时液体在塔板上的流路长度FPL由下式计算:
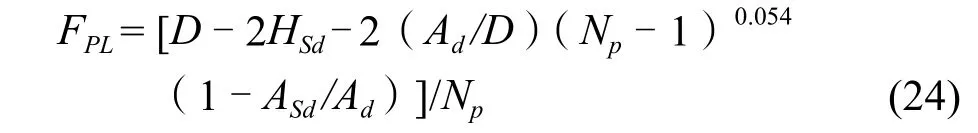
式(24)当Np= 1时,即为单流程的流路长度。
液体在塔板上的平均流路宽度WFP由下式计算:

4.2 筛板塔板的压降计算
筛板塔板的压降依赖于塔内的物流的物料性质,气体流率,液体流率,塔板的开孔大小以及开孔率等因素有关。根据试验数据证明筛板塔在稳定的鼓泡状态的压降稍为大于干板压降和板上净液高度之和,这个差别称为‘过剩’压降。Hunt 等人[5]对于空气—水系统测得过剩压降在10~25 mm水柱之间。Bennet 等人[15]表示过剩压降为克服表面张力压降。因此,筛板塔的总压降可表示如下:

下面就各项予以叙述。
4.2.1 干板压降
最有名也被广泛使用的干板压降公式是1957年Hughmark & O’Connel[6]发表的公式:
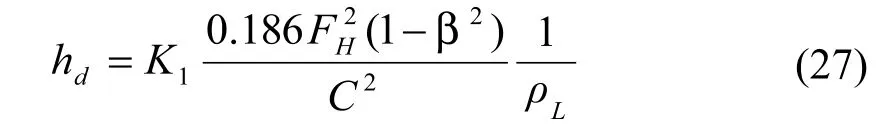
式中:β = AH/ Aa;孔流动摩擦系数C的值与孔径和板厚之比有关,见表4。

表4 式(27)中的C 系数表
对该系数C公式化为:
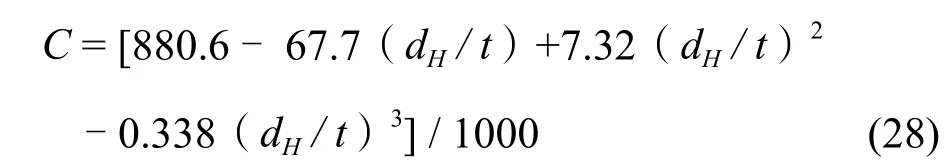
Hunt 等人[5,13]提出如下的公式:
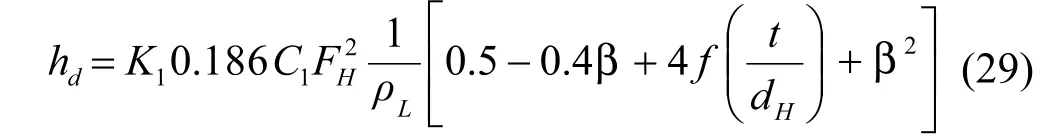
式中:C1=1.09(t / dH)0.25
当 0.5 < (dH/ t)< 5,f = 0.01;
Leibson 等人[14]建立了下式,将开孔面积的比值β放在孔流动摩擦系数C2中,其公式如下:
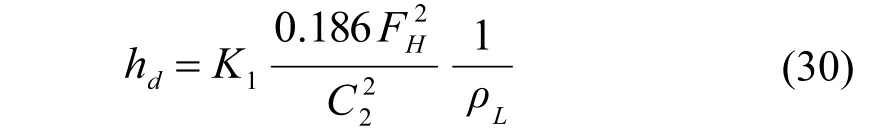
采用下面的公式计算孔流动摩擦系数C2的值:
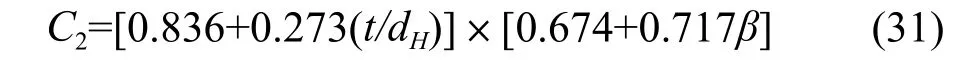
Economopoulos[11]计算得出结论:
由Hughmark & O’Connel 和Hunt 等人的公式计算的干板压降比较接近,采用Leibson等人的公式计算的干板压降值偏高。
本人采用三种公式在图5中标注的条件下对不同的开孔面积比值计算的干板压降值标绘在图5上。
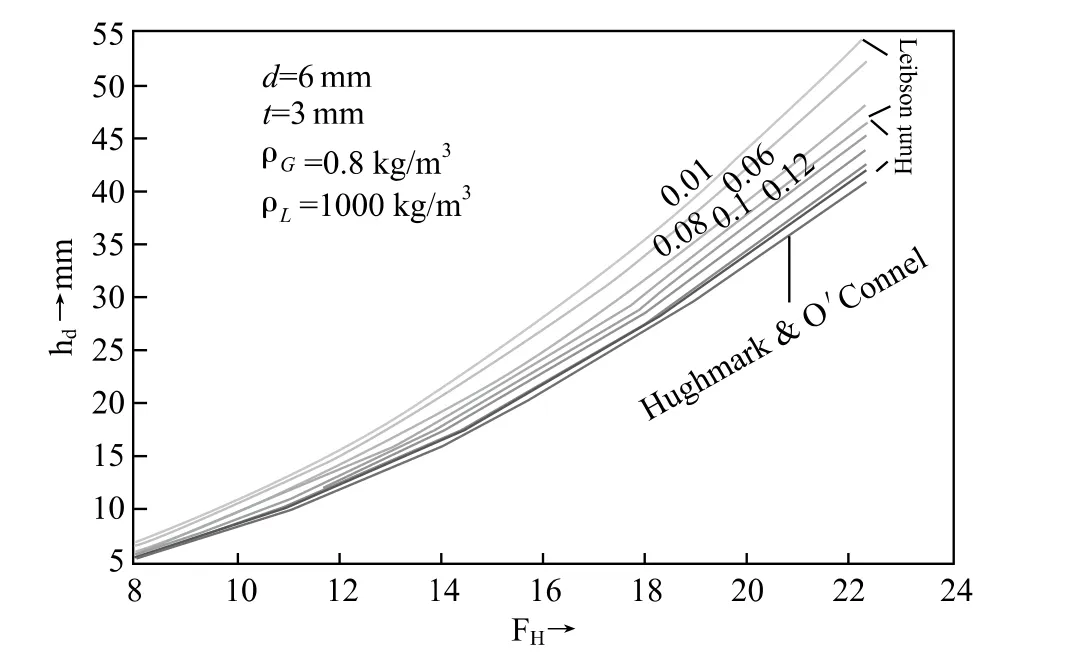
图5 式(27,29,30)计算结果比较图,图中参数为β值
由图5看出Leibson 和 Hunt 的公式对于β值的影响较明显,而Hughmark & O’Connel的公式计算结果基本上看不出其影响,应该说前两者更合理。Hughmark & O’Connel的计算结果偏低,Hunt结果居中。
本人也对表4的数据进行回归,得到如下的公式:
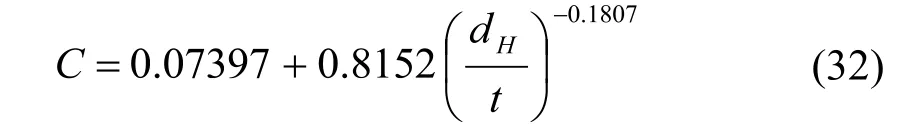
将公式(28)和公式(32)的计算值和表4的数据标绘在图6上,以供比较。
由图6可知:式(32)更符合表4的数据值,但在实际使用中,孔径与板厚的比一般在3~6之间,那时两个公式计算的值基本相近,因此,采用公式(32)更方便一些。
在对于大孔径的筛板时,比如10,15或者25 mm的孔径时,采用式(27)计算干板压降时,其孔的流量摩擦系数C应加大,根据文献[2]的介绍应加大1.15倍,其计算结果比专用大孔径筛板的方法[25]更符合实测值。
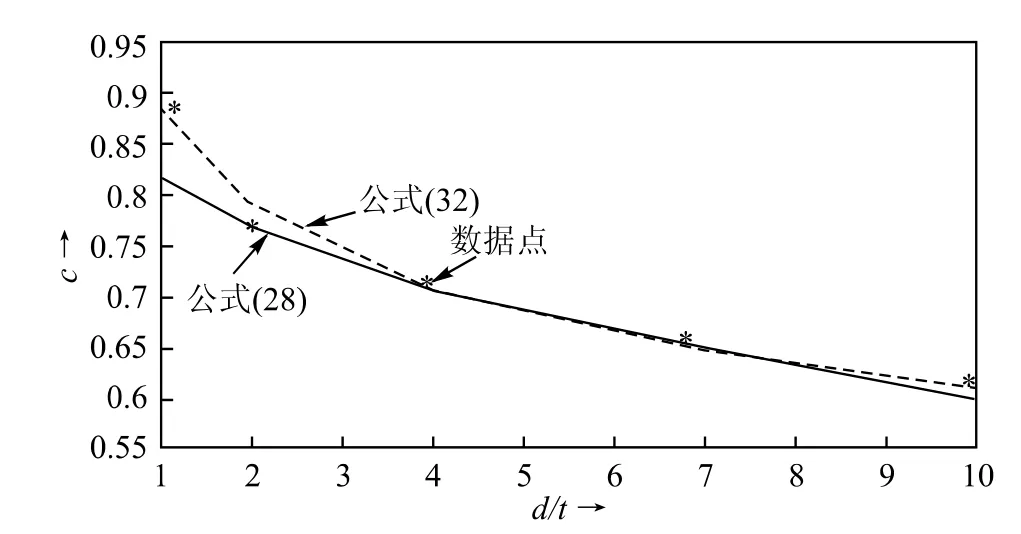
图6 公式(28)和公式(32)的计算值和表4的数据标绘图,图中‘*’为表4的数据点。
4.2.2 板上的净液高度hl
Fair[12]关联了板上的操作液封(hW+ hOW)与板上的被称作充气因子的φ建立了计算板上净液高度的公式(33):
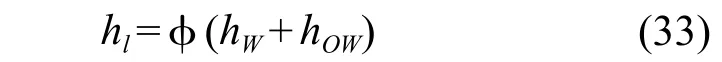
式中:φ充气因子可由下式计算:
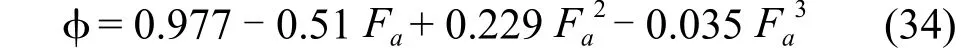
Foss & Gerster[16]用下式计算净液高:
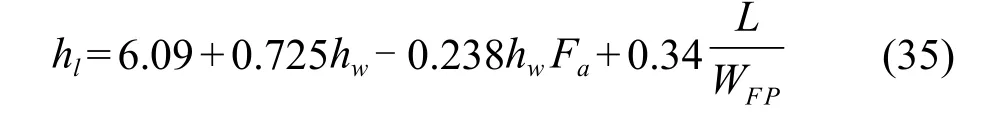
Hughmark & O’Connel 的图可以归纳成下式:
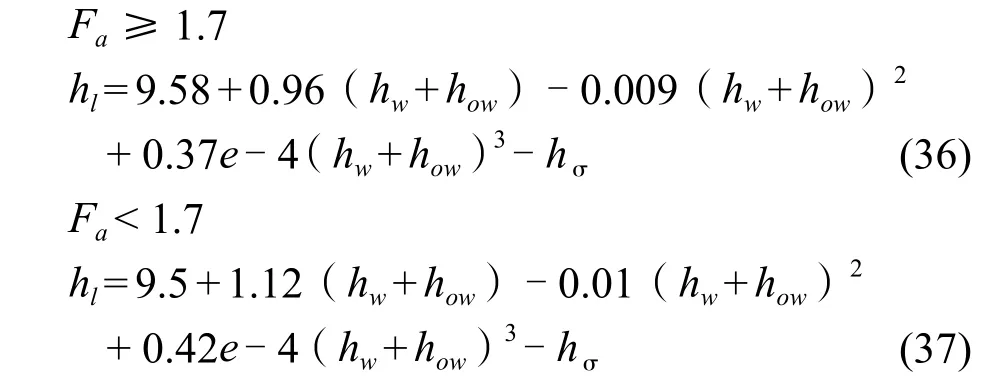
Economopoulos[11]计算得出结论:
Fair 和 Foss & Gerster 两者的计算结果相近,Hughmark & O’Connel 的计算值较大。
1983年Bennett等人[15]建立了新的筛板塔压降计算关联式,其中净液高度的计算式为:
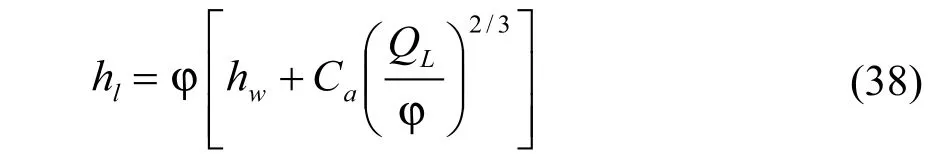
式中:
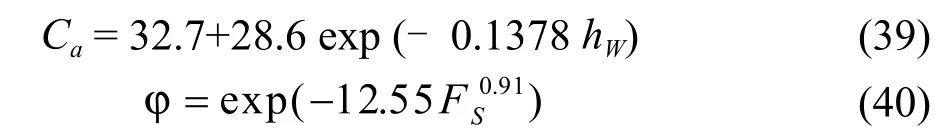
Bennett等人的公式是对不同液流堰高度(0 ~ 100 mm)进行了试验并总结了前人的实验数据,对Bolles的C系数进行了修正,适用性更强。本人对以上四个公式进行了比较计算,结果标绘在图7上。
由图7可以看出Fair公式(33)和Hughmark & O’Connel 的公式(36,37)趋势相同,只不过后者取了平均值。Foss & Gerster的公式(35)和Bennett等人的公式(38)趋势相同,后者大于前者。
对图7的条件不同气速下塔板的总压降进行计算,计算结果标绘在图8上以作比较。
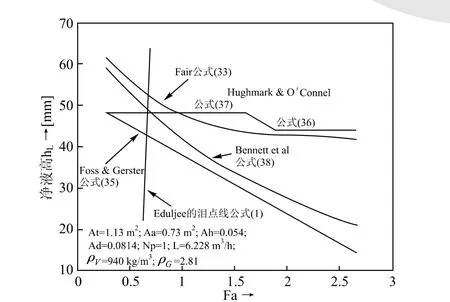
图7 不同气速下四个公式的净液高度值与Fa的关系图
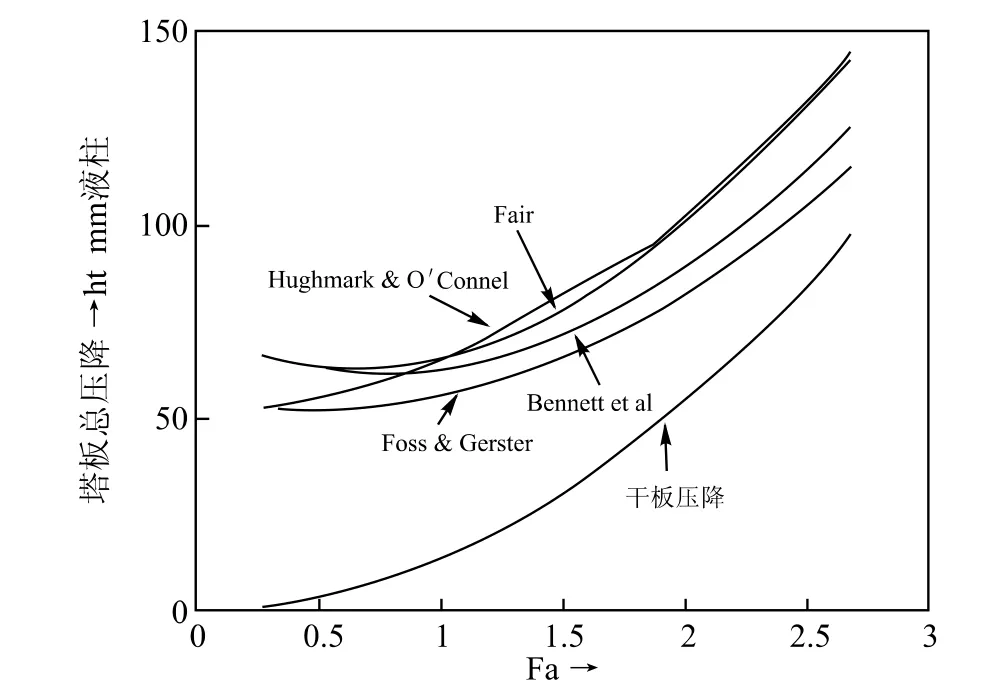
图8 由各个公式计算的塔板总压降比较图
由图8看出:尽管由图7得出的各个公式计算的净液高度有所不同,而且差别较大,但是塔板总压降的趋势相同,且差别有限。这是由于气速越大干板压降所占的比例增加,另外,每个公式计算的各项均有所出入,比如Benneet等人的表面张力所贡献的阻力公式(43)就大于Fair提供的表面张力阻力公式(42)值。从图8的计算结果得出的结论和Economopoulos得出的结论有区别,虽然仅是一个条件的结果,看出Fair 和Hughmark & O’Conne的结果基本相同,而Foss & Gerster和 Bennett 等人的结果较接近,他们的结果低于前两者的结果。至于Kister[38]认为Bennett等人公式局限于孔径小的问题。本人认为孔径的大小关系到干板压降的计算比较多,对于净液高度的影响有限,因而在计算筛板塔的总压降时采用Bennett等人的净液高公式为宜。
在筛板塔板上的泡沫层高度一般推荐下式粗略的估计:

假如以(hW+ hOW)代表hFR对以上各公式计算得到下图9:
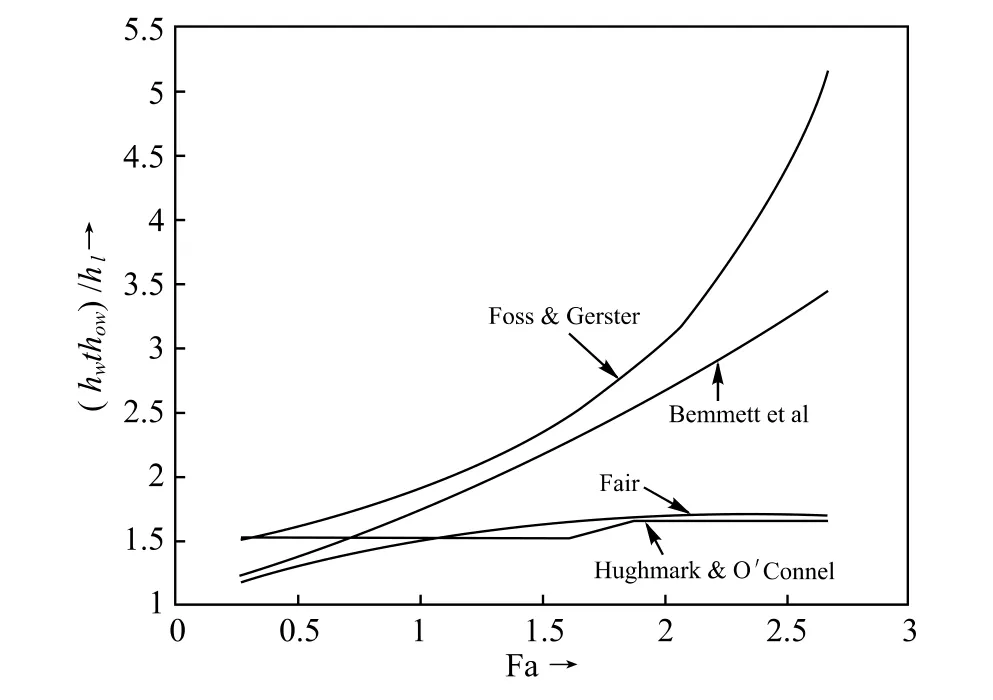
图9 四个公式计算的泡沫层高度与净液高度之比
由图9可以看出只有Bennett 等人的净液高度公式更符合式(41)的关系式。
4.2.3 克服表面张力的压降hσ
气体由孔中形成气泡的必须压力,Fair[12]给出下式:

Bennett 等人[15]的公式为:
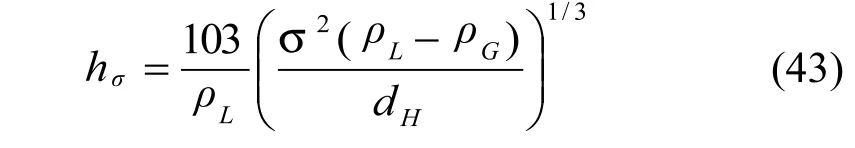
从计算结果来看,式(43)的结果往往高于式(42)。
4.3 筛板塔的液泛和雾沫夹带4.3.1 筛板塔的雾沫夹带
最常用的是由Fair[26]1961年发表的图(10)来估计雾沫夹带量。
由图10依据Fair的气液流动参数FLV和液泛百分率Ff查得雾沫夹带分率ψ:也可按下式(44)来计算雾沫夹带分率ψ:
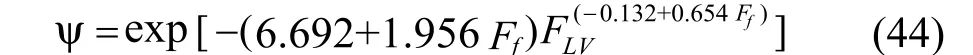
由式(44)计算出ψ值,再由式(45)计算雾沫夹带量e为:
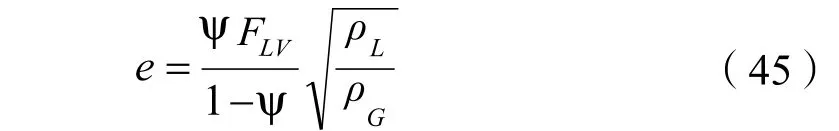
一般设计推荐雾沫夹带量应小于0.1。
在文献[18]中关于雾沫夹带对于Fair公式、Hunt公式以及Kister公式进行了探讨,结论是Fair公式适用于较宽的流动因子范围,而且在工业上还是被认可的计算公式。对于Fair的公式与Bennett公式也作过比较,后者的结果往往大于前者。由此本文推荐采用fair方法。
4.3.2 筛板塔的液泛
筛板塔的液泛基本上和其他板式塔的液泛性质是一样的,比如浮阀塔板。关于这方面的叙述,在齐福来“浮阀塔板的设计及流体力学计算探讨”一文[18]中有详细的叙述,本文就不累述了。
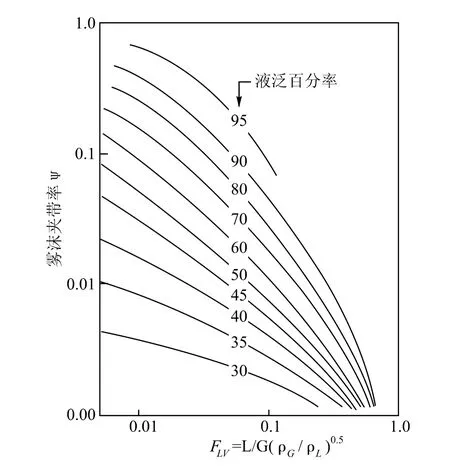
图10 雾沫夹带份率ψ与FLV的关系图,图中参数为液泛百分率Ff
4.4 筛板塔板的效率计算
筛板塔的效率一般是符合板式塔的板效率的规律,在研究中有的采用全塔效率,也有的采用点效率,板效率等。在预言板效率时有采用经验关联法典型的如O’Connel法,也有采用理论研究法如Murphree。
4.4.1 双膜理论研究方法
Murphree[27]采用板效率替代点的效率:
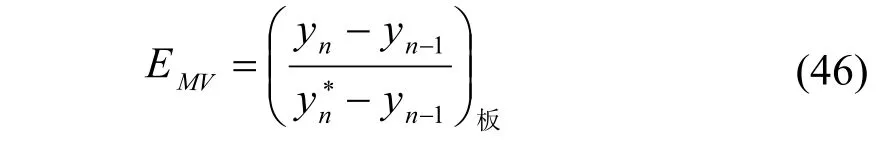
Lewis[28]采用Murphree板效率按下式计算全塔的效率:
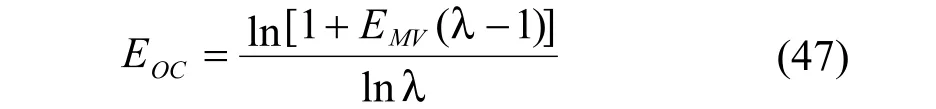
式中:

Murphree 的点效率关系到气体和液体的传质单元数NG,NL;
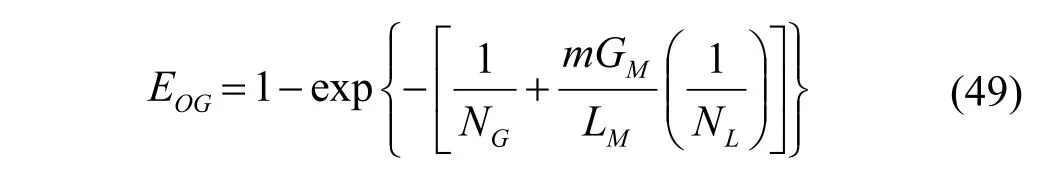
AIChE 手册[29]列出了计算NG的经验关系式:
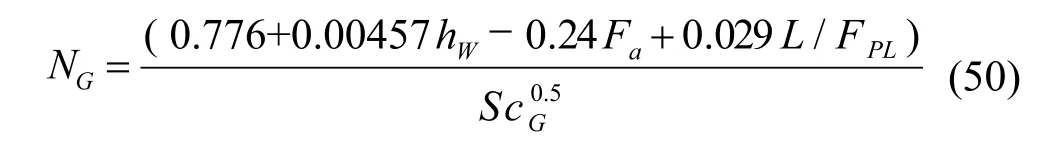
式中:ScG= μG/ ρGDG
Foss & Gerster[30]给出 KLa的值就可求得NL:
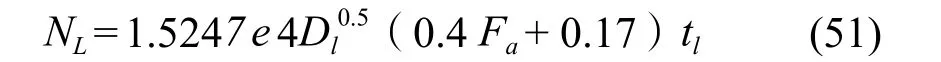
Hughmark[31]得到一个新的对于由液相传质控制时更准确的关联式来计算NL和NG:
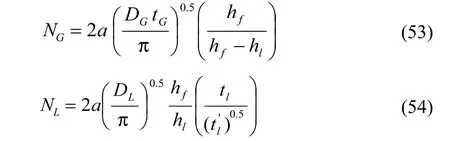
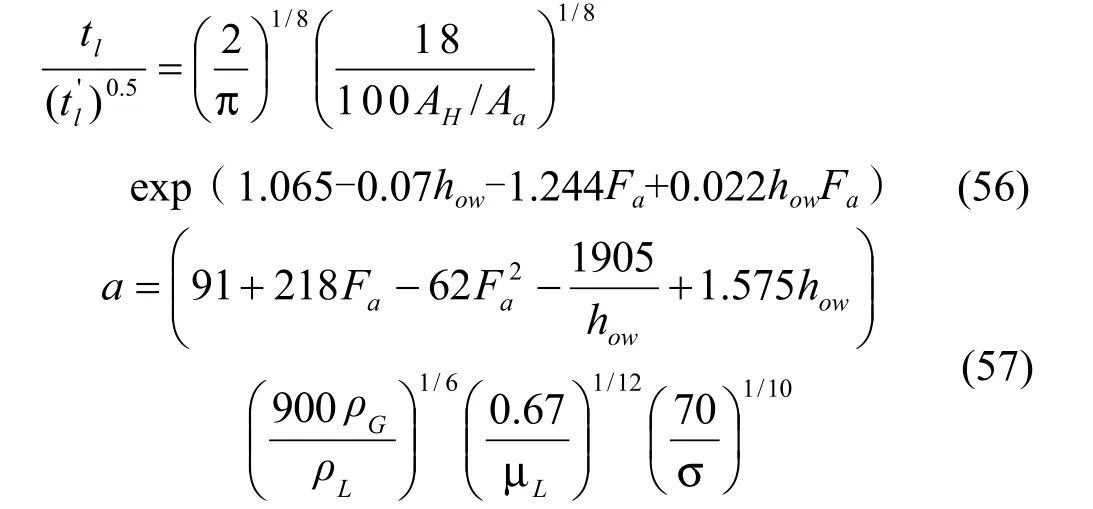
他也给出了计算泡沫层高度的计算公式:
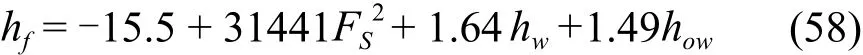
基于在板上液体混合的模型即气相全混型,液相为活塞流,考虑了液体的反混,AIChE手册将Murphree点效率和Murphree板效率关联如下:
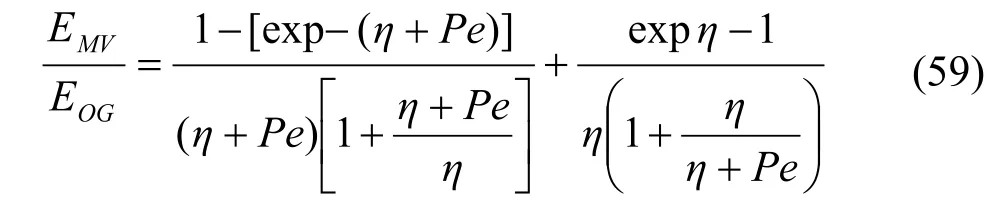
式中:
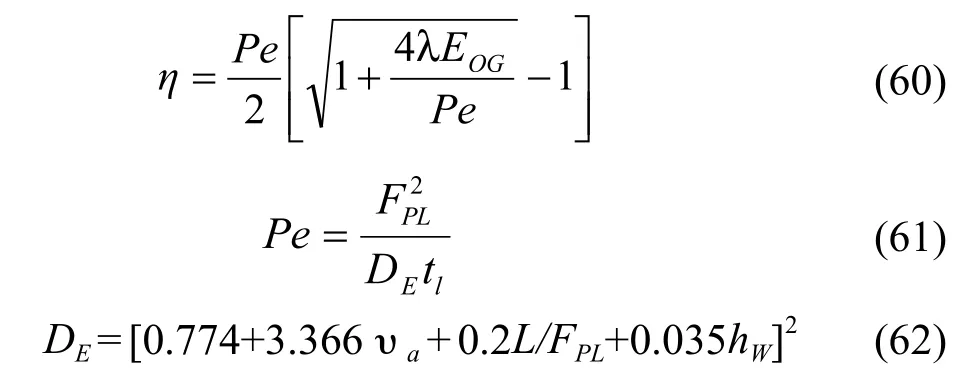
Barker and Self[32]按下式计算DE:
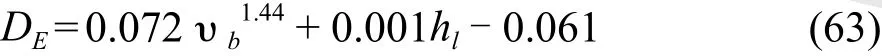
Wilke and Lee[39]按下式计算DG:
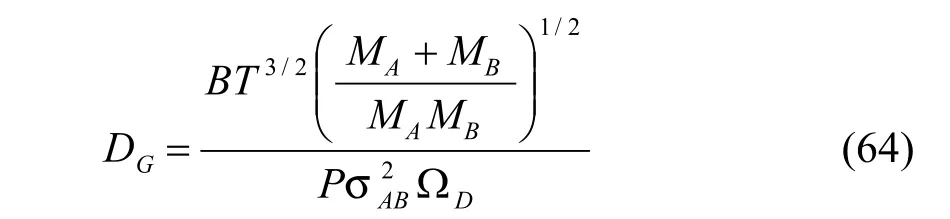
式中:
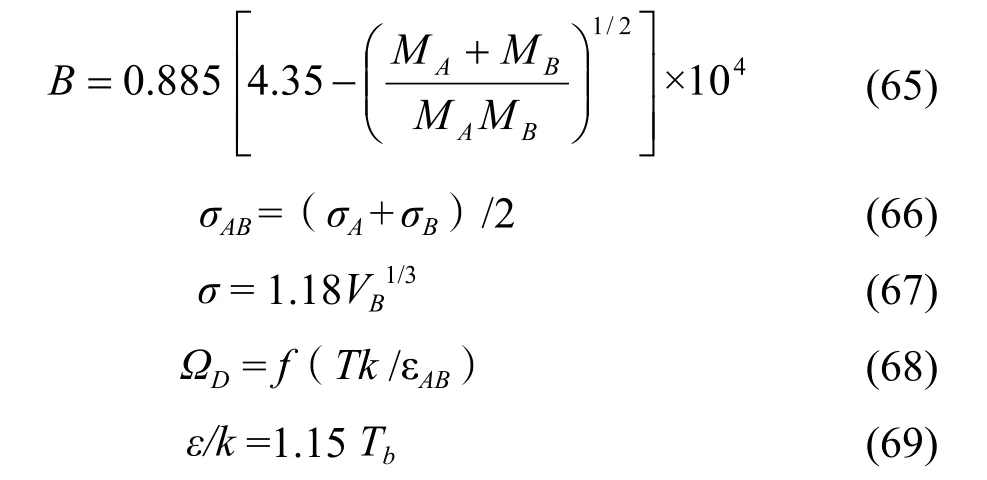
式(68)的函数关系如下图11。
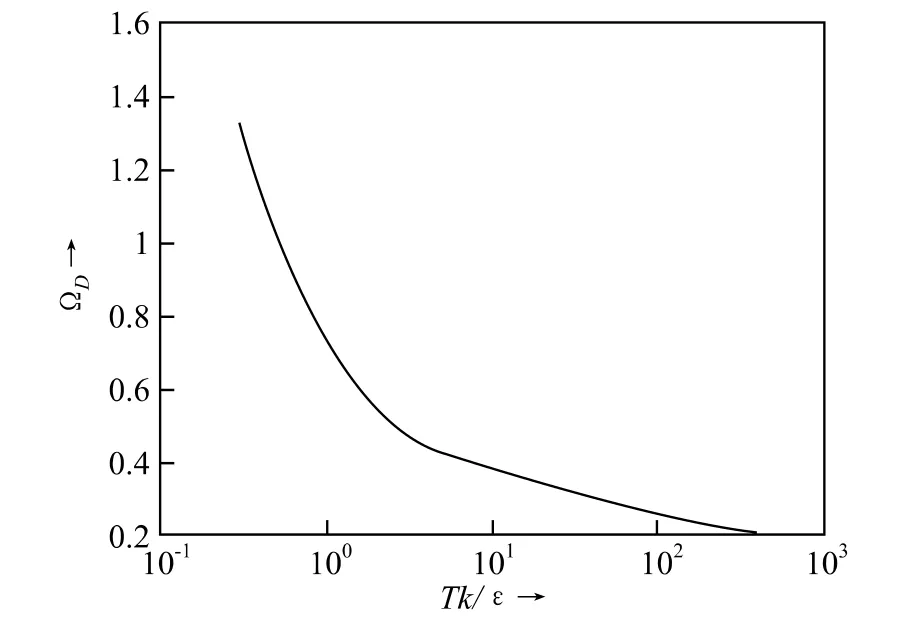
图11 ΩD和Tk /ε的关系图
图11可公式化为:
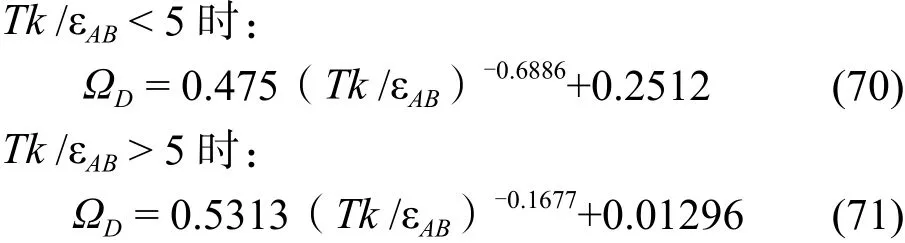
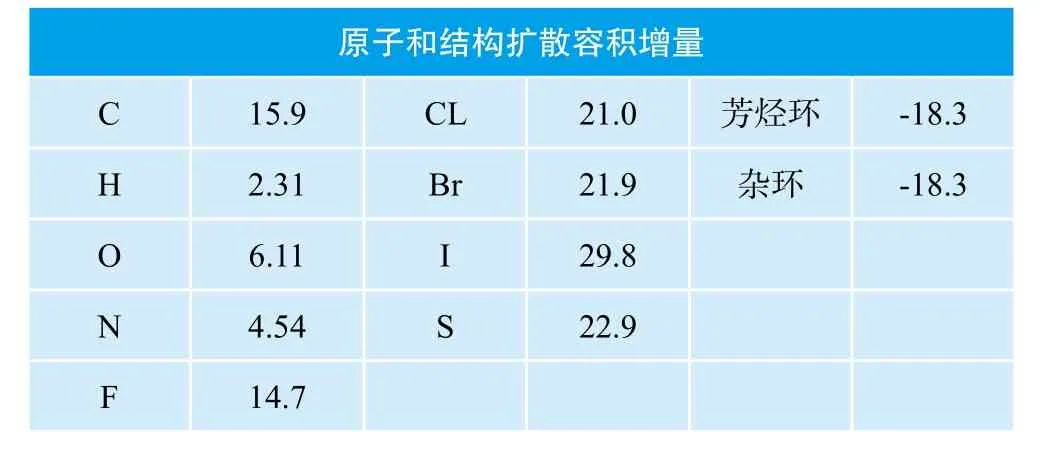
表5 原子扩散容积VB表
液相扩散系数采用Wilk-Chen[40]的方法:
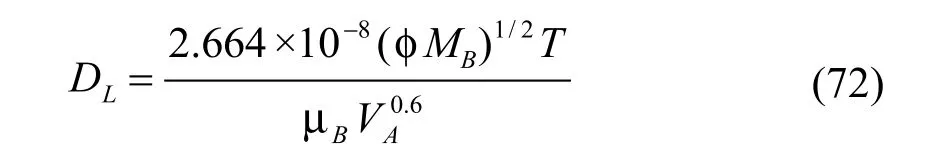
式中:φ为溶剂的缔合因子,他们建议对于水为2.6,对于甲醇为1.9,对于乙醇为1.5,对于不缔合的溶剂为1.0。
Colburn[33]给出由于雾沫夹带引起的效率变化:
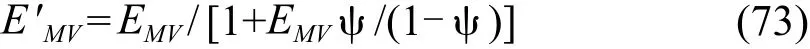
式中:ψ由式(44)计算。
4.4.2 经验关联法
O’Connel[34]依据31个蒸馏装置的塔板效率数据绘制了对进料组分的相对挥发度与黏度乘积的关系图12。

图12 O’Connel 对于蒸馏塔塔板效率估计图
Lockett[35]将该图12公式化为:
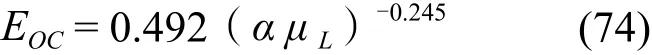
O’Connel 关联图基本上是基于泡罩塔的数据,有人[36]认为应用于筛板塔和浮阀塔似乎稍微保守一点。
Drickamer & Bradford[37,12]依据54个蒸馏塔的数据绘制了塔效率和进料黏度的关系图,他的图可以归纳成下式:
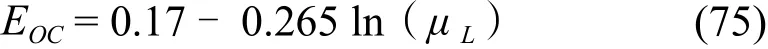
5 计算软件‘SieveTray’的应用
5.1 “SieveTray”软件的功能
5.1.1 计算塔径和流体力学数据
提供的条件如下:
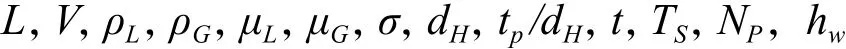
其中L,V也可以输入LM,VM,但那时就必须输入M分子量的值。
通过计算得到的值为:
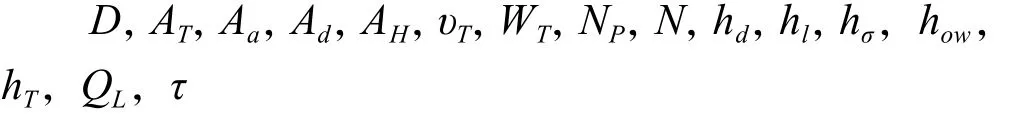
5.1.2 根据要求可以计算塔板的效率
要求输入的值:
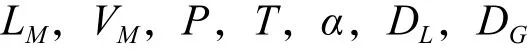
如果不知DL,DG的值可以要求计算这两个值,那就必须输入:
溶质与溶剂的原子数目;
TA,μB,溶剂B的类型;
计算得到:
AIChE 方法考虑雾沫夹带的EMV;
Hughmark方法考虑雾沫夹带的的EMV;
Drickamer的全塔效率EOC;
O’Connell 的EOC;
5.1.3 可以得到操作负荷图。如下图:
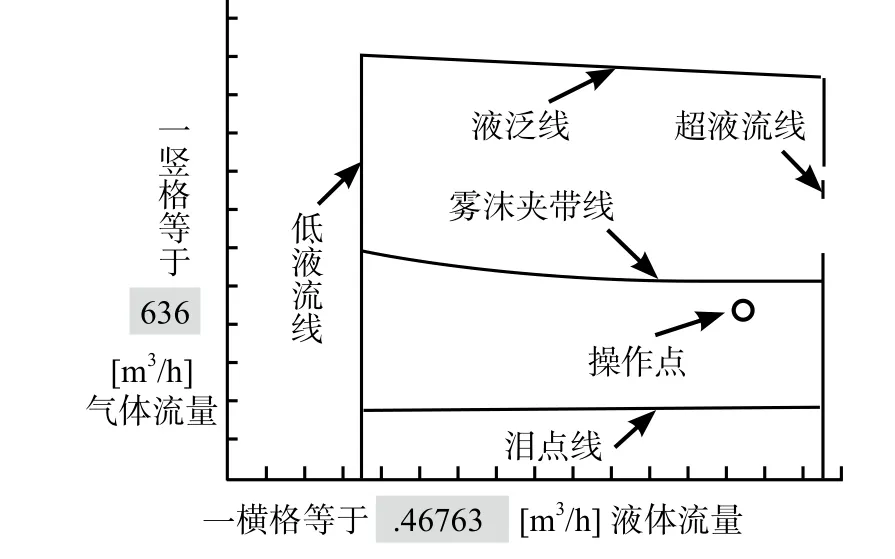
图13 操作负荷图
按图13可以对设计的条件进行修改,以达到满意的结果。
5.2 举例说明其应用
5.2.1 某二甲苯塔的设计条件如下
L = 26.62 m3/h, V = 5838.7 m3/h,
ρL= 805 kg/m3, ρG= 3.67 kg/m3,
μL= 0.25 mP/s, μG= 0.008 mP/s,
σ = 20 mN/m, dH= 13 mm, TS= 600 mm,
tp/ dH= 3.5, t = 3 mm, hw= 50 mm
首先打开‘SieveTray’’软件看到下面的屏幕:
图14 说明屏幕
然后揿‘确定’按钮的下一屏幕的右边屏幕:

图15 选择和计算启动的‘计算说明部分’屏幕
在计算类型中选择‘设计’,然后打开‘输入操作和结构数据’屏幕,并将有关数据填入,即为下一屏幕:

图16 输入操作和结构数据屏幕
再打开‘输入物性数据‘屏幕,填入物性数据如下屏幕:
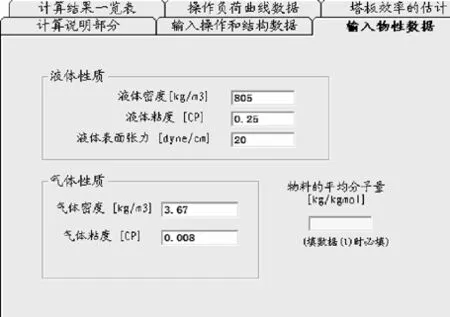
图17 输入物性数据屏幕
假如不要计算塔板效率,我们的数据就算填写完毕了,再回到‘计算说明部分‘屏幕揿‘计算‘按钮。
计算结束时,在‘计算情况汇报框’会返回计算的结果。在‘计算汇报框’有时会返回出了问题,希望再进行数据的修改,或者缺少数据等。如果计算成功就返回说明塔板上的操作情况。如图18:

图18 返回到‘计算说明部分’屏幕
这说明计算完成了,其结果就在‘计算结果一览表‘打开’计算结果一览表’如下:
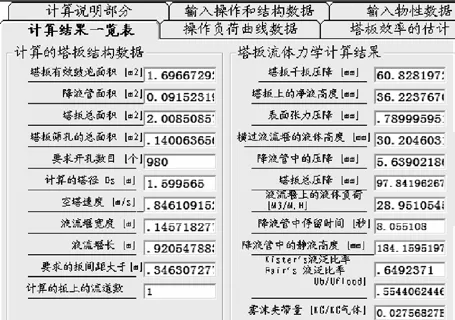
图19 ‘计算结果一览表’屏幕
5.2.2 计算结果汇总
塔直径D = 1.599 m;
开孔数 N = 980;
有效塔板面积Aa= 1.69 m2;
降液管面积Ad= 0.0915 m2;
液流堰长 Wsd= 0.92 m;
塔板总压降hT= 97.84 mm液柱;
空塔速度υT= 0.846 m/s;
液泛比率:Kister 0.649
Fair 0.5544
雾沫夹带0.0275 kg/kg;
5.2.3 画操作负荷图
要看操作点的位置就揿左面屏幕的‘画负荷图’按钮,就可以得到一张负荷图如图20:
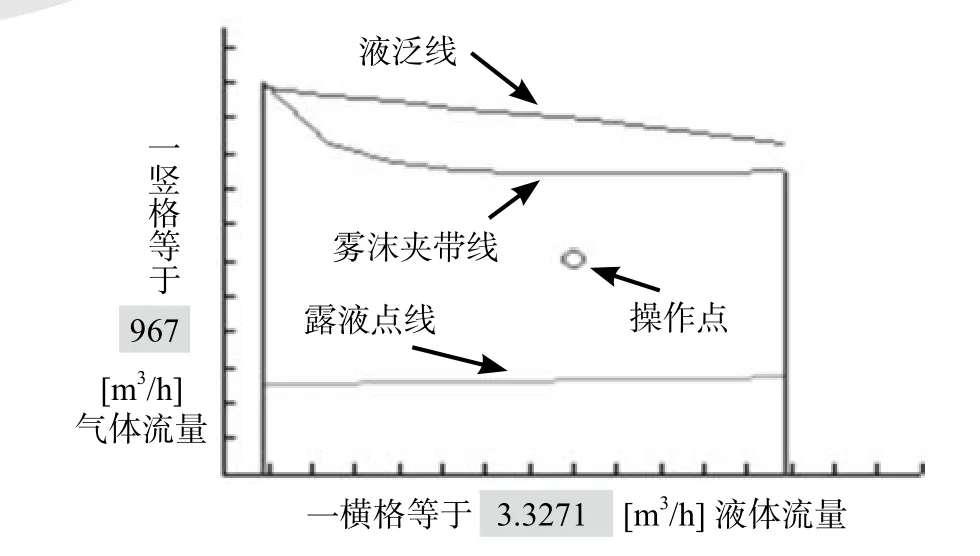
图20 画负荷图屏幕
图20中对各条线均予以说明。由图20看来操作点基本位于中心点位置,还是比较合理的。
5.2.4 对结果进行验证
由式(11)计算:
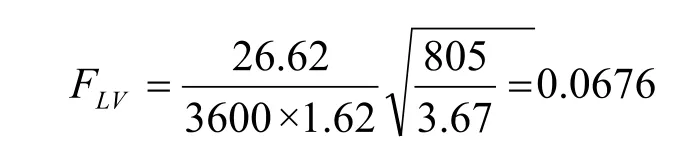
由式(3)计算CSbf:
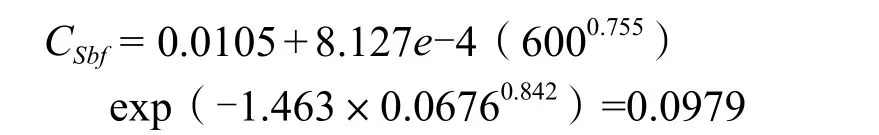
由式(2)计算UNF:
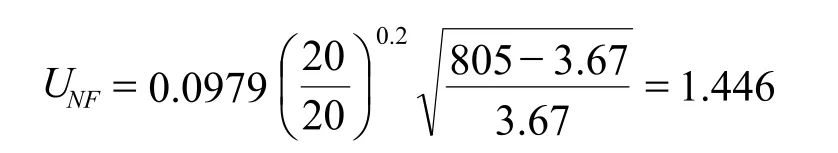
这个是液泛气速,根据图3我们选择60%的液泛气速。
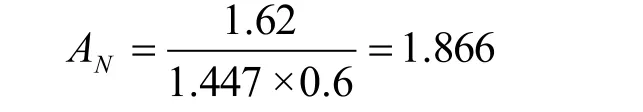
由4.1.2节的要求求得Ad:
Ad= 26.62/250 = 0.10
AT= AN+ Ad= 1.866 + 0.10 = 1.966
D =(1.966/0.785)0.5= 1.58
从塔径的计算结果来看1.58 m和1.599 m都会圆整到1.6 m的结果。
从液泛的计算值:Kister的值为63.5%,Fair的值是54.3%。
在计算完后对计算结果进行分析,可以对某些值进行修改,比如:孔数,塔径,降液管面积。进入‘输入操作和结构数据’屏幕,填写改变后的三项值,在其它输入的数值不变的情况下,返回‘计算说明部分’勾‘模拟’框,然后揿‘计算’按钮,则会进行模拟计算,其结果会从新改写,并可以在原负荷图上覆盖新的负荷图。通过反复的修改,就可以找到合适的设计条件。
5.2.5 塔板效率的计算
塔板效率的计算在填写数据时,可以数据(1)的单位填写气液流量,也可以数据(2)填写。按照5.1.2的要求数据填写。一般情况人们都要求计算扩散系数,因此,在填写‘计算说明部分’屏幕时应如下所填:
图21 计算塔板参数和塔板效率屏幕
按照前面的例子填写‘输入数据和结构’屏幕:
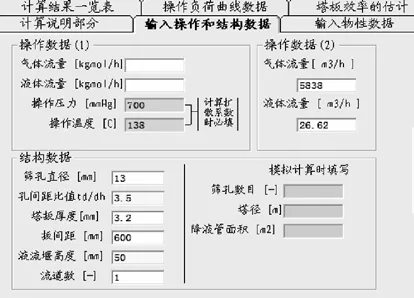
图22 计算塔板效率时‘输入操作和结构数据’屏幕的填写内容
填写内容和图16相同,但必需填写咖啡色框中的操作压力和操作温度两项。
填写‘输入物性数据屏幕’时和前面图17相同。接下来打开‘塔板效率的估计’屏幕。
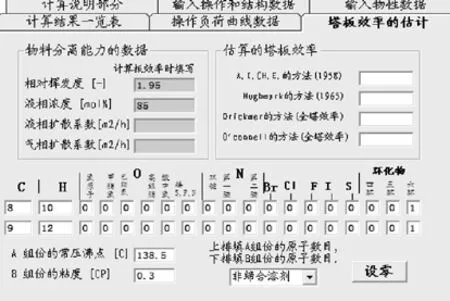
图23 ‘塔板效率的估计’屏幕的填写要求图
首先填写轻、重关键组分的相对挥发度α,然后填写轻关键组分的平均液相浓度。在填写计算扩散系数的部分时,首先揿‘设零’按钮,那时下方的两排小方框内均为零。然后分别填写轻、重两个关键组分的原子数目。再下来填写轻组分的常压沸点以及重组分的黏度,对溶剂的缔合情况进行选择。填完图23的内容后返回‘计算说明部分’屏幕,揿‘计算’按钮,‘计算结果一览表’的内容和图19相同。再打开‘塔板效率的估计’屏幕时看到在估计的塔板效率处有计算的结果,如图24:

图24 塔板效率计算结果屏幕
在该屏幕中计算的气-液相扩散系数和各公式的计算效率值都标注在框内。
说明:
(1)当不知道塔板上的流程数目时可填写NP= 1,但当计算结果显示NP= 2或者4时,应该重新填写流程数进行新的计算。当发现板上流程数的增加塔径会缩小时就要看经济性了,一般来讲流程数越少越经济,但也不能作为规则,要根据具体情况决定。
(2)本软件在计算收敛方面采用边值条件,在允许范围以内就可以了,因此,计算结果并不一定是最佳结果,应该通过使用者的判断以及反复计算就会得到你认为合适的设计条件。
(3)该软件并非完美的软件,但可以帮你省去繁复的手算工作,极快的完成筛板塔的设计计算任务。
符号说明
Aa— 板上的有效面积,m2;
Ad— 板上总的降液管面积,m2;
AH— 板上的开孔面积,m2;
ASd— 塔侧降液管面积,m2;
AT— 全塔面积,m2;
B — 式(65)定义的系数;
C — 式(27)的孔的流动摩擦系数;
Ca— 式(39)定义的参数;
CAF,CAFo— 塔板的容量因子;
dH— 孔径,mm;
D — 塔径,m2;
DL— 液相扩散系数,m2/h;
DG— 气相扩散系数,m2/h;
DE— 涡流扩散系数,m2/h;
EMV— Murphree 板效率;
E ′MV— 受雾沫夹带影响的板效率;
Ept— 总效率;
EOG— Murphree点效率;
EOC— O’Connel 的塔板效率;
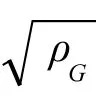

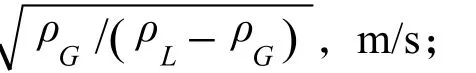
FLV— Fair的气液流动参数;
FPL— 液体在板上的流路长度,m;
GM— 气相重量分子流率,kgmol/h;
HSd— 弓形降液管的弦高,m;
h — 高度,压降,mm液柱;
k — Boltzmann 常数;
K1— 式(1,5)的单位换算系数,K1=273.4;
L — 液体流量,m3/h;
LM— 液相重量分子流率,kgmol/h;
m — 气液平衡线的斜率;
M — 分子量,g/mol;
N — 开孔数目;
NP— 塔板上的流程数;
NG— 气体传质单元数;
NL— 液体传质单元数;
QL— 单位长度液流堰上的液流强度,m3/min · m;
SF— 系统特性参数;
t — 板厚,mm;
tl— 液体在板上的停留时间,h;
tp— 孔间距,mm;
T — 绝对温度,°K;
TS— 板间距,mm;
Tb— 溶剂的正常沸点,°K;
TA— 溶质的沸点,°K;
yn,yn-1—第n块板和第n-1块板上的分子浓度;
V — 气相流量,m3/s;
Vload— 式(5,9)中的气相负荷参数;
WT— 塔板上的总堰长,m:
WFP— 液体在板上的平均流动宽度,m;
WSd— 塔板上的弓形降液管的堰长,m。
无因次准数
SCG— 气相施密特准数;
Pe — 派克列准数。
希腊字母
α — 相对挥发度;
β — Ao/Aa,开孔面积与有效板面积的比率,[-];
ε — Lennard-Jone 能量;
η — 式(60)定义的变量;
λ — 式(48)定义的变量;
μ — 黏度,cP;
ρ — 密度,kg/m3;
σ — 表面张力,dynes/cm;
σ — 式(67)定义的Lennard-Jone分子特性长度,Å;
τ — 在降液管中的停留时间,s;
υH— 基于孔内面积的气速,m/s;
υa— 基于有效面积的气速,m/s;
υb— 基于鼓泡区的面积气速,m/s;
υT— 基于全塔面积的气速;
Φ — Fair公式(33)的充气因子;
φ — Bennett公式(38)定义的液含率;
ψ — 雾沫夹带分率;
ΩD— 分子的碰撞积分。
[1] 清华大学化工系. 大孔径筛板塔的研究[J]. 化学工程,1972, (4):85.
[2] 燃化部第六设计院. 石油化工设计化学工程建设组. 气液传质设备设计,化工单元操作设计参考资料(四),1973.
[3] E.E.Ludwig. Applied Process Design for Chemical and petrochemical Plants. Voume 2, 3rd, Gulf Publishing Company, 1979.
[4] F. D. Mayfied,W. L. Church,A. C. Green, D. C. Lee, and R. C. Rasmuseen. Ind. Eng. Chem, Vol. 44, 2238 1952.
[5] C. A. Hunt, D. N. Hanson and C. R. Wilk. A. I. Ch. E. Journal. Vol. 1, 441, (1955).
[6] G. A. Hughmark, and H. E. O’connel. Chem. Eng. Progress, Vol. 53, 127-M, (1957).
[7] P. A. Kolodzie, and M. van Winkle, A. I. Ch. E. Journal. Vol. 3, (1957)
[8] P. L. Smith, and M. van Winkle. A. I. Ch. E. Journal, Vol. 4,(1958).
[9] D. S. Anold, C. A. Plank, and E. M. Schoenborn, Chem. Eng. Progress. Vol. 26, 1038 (1952).
[10] R. A. McAllister,P. H. McGinnis, and C. A. Plank. Chem. Eng. Science. Vol.9, 25 (1958).
[11] A. P. Economopoulos, Computer Design of Sieve Trays and Tray Columns. Chem. Eng. (1978).
[12] J. R. Fair, Chapter 15. Design of Equilibrium Stage Processes. B.D. Smith McGraw-Hill, (1963).
[13] R. E. Treybal. Mass Transfer Operations. 2nd, McGraw-Hill New York,1968.
[14] I. Leibson, R. E. Kelley, and L. A. Bulliongton. Petr. Refiner, Feb, pp127, March, pp288, (1957).
[15] D.L. Bennet,R. Agrawal,and P. J. Cook, New Pressure Drop Correlation for Sieve Tray Distillation Columns. AIChE. Journal. Vol. 29,No.3 P434, (1983).
[16] Foss & Gerster. Chem. Eng. Progress, Jan.p28,(1956).
[17] H. E. Eduljee. The Design of Sieve-Type Distillation plates. British Chem Eng., Vol.4, Jan. p320-326, (1959).
[18] 齐福来. 浮阀塔板的设计及流体力学探讨[J]. 医药工程设计,2007, 28(1): 5.
[19] H.E.Eduljee. Chem. Age. India, Vol.17,No.9 (1966).
[20] J. R. Fair. Petro./Chem. Eng, Vol.33,No.10 (1961).
[21] A. L. Lygeros, K. G. Magoulas. Column Flooding and Entrainment. Hydrocarbon Procees. 65(12) 43 (1986).
[22] Ind. Eng. Chem. Process Dev. Develop. 22,53,(1983) .
[23] Glitsch Inc. Balast Tray Design Mannual. Bulletin No. 4900, Dalas, Tex, 1974.
[24] Koch Eng. Co.,Inc.. Flexitray Design Mannual. Bulletin 960, New York, 1960.
[25] U. Subdermann. Chem. Tech., Vol. 19, No. 5, pp267, 1967.
[26] Fair, J.R., Petr/Chem Eng. 33 (10), p45, 1961.
[27] E. V. Murphree. Ind. Eng. Chem. Vol. 17, p.747 ,1925.
[28] W. K. Lewis. Jr. Ind. Eng. Chem. Vol.28, p339, 1936.
[29] AIChE. Bubble Tray Design Mannual. New York, 1958.
[30] A. S. Foss, and J. A. Gerster. Chem. Eng. Prog. Vol. 52, No, 1, p.28, 1956.
[31] G. A. Hughmark. Chem. Eng. Prog. July, 1965, p. 97.
[32] P. E. Barker, and M. F. Self. Chem. Eng. Sci. Vol.17, p541, 1962.
[33] A. P. Colburn. Ind. Eng. Chem. Vol. 28, P526, 1936.
[34] H. E. O’Connel. Trans. AIChE, Vol.42, p741, (1946).
[35] M. J. Locket. Distillation Tray Funda-mentals. Cambridge Univ. Press, (1986).
[36] P. C. Wankat. Equilibrium Staged Sepa-rations. Elesvier, New York, (1988).
[37] H. G. Drickamer, & J. R. Bradford. Trans. Am. Inst. Chem. Eng. Vol. P319, (1943).
[38] H. Z. Kister. Distillation Design. McGraw-Hill,Inc. 1992.
[39] C. R. Wilke, and C. Y. Lee, Ind. Eng. Chem.Vol.47, p1253 1955.
[40] C. R. Wilke, and P. Chen. AIChE J, Vol.1, p264, 1955.

