无相变热交换器的尺寸选择

齐福来

（中国石化集团 上海工程有限公司，上海 200120）

1 前言

热交换器在各个工业部门都是非常重要的和非常多的设备。不管是军用还是民用，不管是石油化工，医药行业还是炼油行业，为了节能就要建立一整套的热交换网络，回收热能。在某些化工车间内热交换器设备占设备总量的45%以上。然而热交换器的形式很多：套管式、喷淋管式、固定管板式、螺旋板式、板框式等。固定管板式热交换器无疑是使用得最多的一种，这主要是由于它的制造技术比较成熟，而且造价低，又有比较现成的图纸好套用，在国外有TEMA[1]标准，在我国也有(JB/T 4715-1992)[2]标准，因此对它的采用就比较广泛。

如何设计和选择一个满足要求的固定管板式热交换器？在新建工厂或者在技术改造中必须回收热能时所遇到的现实问题。对于有经验的设计者来讲首先根据物料性质，物料的温度级别，决定什么物料适合于走管程，什么物料走壳程。还有很多的工艺条件以及制造条件的限制，比如：热交换器的管长限制；壳程压力降的限制；管程压力的限制；第二步假定总的传热系数以及现实的平均温度差求得传热面积。第三步根据流体在管内的经典流速决定管数。第四步根据所草拟的热交换器尺寸数据再套用我国的标准来决定热交换器尺寸来计算管程和壳程的传热系数和压力降，根据计算结果再进行尺寸调整，一直到满意的结果为止。

由于这个计算过程是一个试差运算过程，非常麻烦。因此，在很多情况有经验的工程师就根据现有的情况，以及传统的传热系数和温差大概估计一下，套用国家标准选用合适的固定管板式热交换器。这种现象是很普遍的现状。由于没有详细的运算，选用的设备一般是比较富裕的，增加了投资。

热交换器的选择不是一个特定的解，而是一个可允许的范围。它是由壳程压降、管程压降、最长和最短的管长限制所包围起来的一个区域，在这个区域的所有尺寸的热交换器都将适合于工程上的传热需要。

1996年Podder & Polly[3]发表了通过参数画图来设计热交换器的文章。以纵坐标表示壳径，以横坐标表示管长。在图中有两条横的平行线，上面的一条是最小的管内速度限制线，下面的一条是最大的管内速度限制线。有一条曲线是满足传热要求的限制线。由上边的两条平行线和这一条曲线以及纵轴所围成的多边形区域就是满足我们工况要求的所有热交换器尺寸。这个满足传热要求的曲线还和壳程压降限制线有一个交点，这个交点所对应的热交换器就是最经济的热交换器的尺寸。有时为了保险，取10%的保险系数，那么该满足传热的曲线就上移适当的部分。

问题是我们如何找到这个满足我们工况要求的传热曲线，然后找到适合我们的最经济的热交换器！为达到此目的就必须做大量的计算工作，这只有由计算机来帮我们完成这样的工作。为此本人用Visual Basic 6.0语言编制如下的程序‘HeatExchanger’

来解决这个问题。

2 该软件建立的条件和思路

2.1 建立该软件的基本条件的决定

固定式管壳式热交换器的形式按照TEMA的规定：前封头A，B，C，D，后封头L，M，N，P，S，T，W等形式。壳程为E，F，G，H，J，K等形式。对于液-液热交换器一般前封头多采用A，B形式，壳程多采用一程的E形式。热交换器的管子排列有正方形和三角形两种，依据流动方向有直列排布与错列排布。正方形排布的目的是为了管外的清扫以及压降的降低。从传热角度来说三角形排布更有利一些，三角形排布一般采用正三角形的排布。因此，在编制程序时考虑壳程采用E式一壳程，管程可以为1，2，4，6程。管子的排布采用单一的正三角形排布。管子排布的管心距一般是管外经的1.25倍。热交换器采用的管径一般有两种φ19×2和φ25× 2.5。折流板间的距离、折流板的开口大小、管束与壳体的间隙、管子与折流板之间的间隙、折流板与壳体之间的间隙等因数有关。折流板的间距可以根据壳体直径的大小来决定，TEMA推荐最小值是壳体直径的20%，最大值考虑管子的强度支撑φ19× 2的管子为1.5 m，φ25×2.5的管子为1.8 m。

2.2 建立该软件的思路

不管换热器多长，计算就是依据这短短的两个折流板之间的流动状况来决定的，这也就是液液热交换器的基本单元。只要决定了这个基本单元的各要素就决定整个热交换器的大小。在§2.1已经确定了管子的大小，管间距以及排列方式，折流板之间的间距也初步确定。管子和折流板之间的间隙，折流板与壳程之间的间隙，根据不同的标准（TENMA，JB/T 4715-1992）有不同的规定。由这些规定我们就可以决定这个热交换器的基本单元的尺寸。

在这个基本单元中的传热：一个是管内的传热，另一个是壳程该单元的传热。管内的传热根据物料的性质以及流动状况就可以根据Hausen[4]和Colburn[5]的公式计算而得。对于壳程的传热比较复杂，过去一直采用Kern[6]的方法，上个世纪后半期就开始对壳程的旁路对壳程传热的影响加以重视，先后有Bell[7]法和Tinker[8]的用于计算机计算的流路分析法。后来又由Wills-Johnston[9]发表了他们的较简单的计算壳程的传热系数的流路分析法。在齐福来[10]的文章里对这几种方法进行了比较，其结果证明Kern的方法比较保守。作为一种研究的软件在设计时考虑了不同方法的比较，让使用者有个参考和分析决定的余地。

在这个基本单元中的压降计算：管程的压降计算采用Churchill[2]开发的单一的适用于所有Re数范围的公式。壳程的压降计算采用了上边三种方法进行了计算，其结果Kern[6]的方法压降值最大，有时是数量级的差别。

假如忽略由于温度的变化引起物料物理性质的变化所产生的传热和压降的变化，就可以依据该传热单元的数据来估计所需热交换器的管长和壳径的尺寸。为了正确性就必须对物性的选择做一个平均值的考虑。

在计算的过程中套用标准[1，2]的热交换器尺寸从小到大进行筛选，适合传热和压降需要的热交换器记录在册。并对最小的也就是传热系数最大的热交换器予以选择。

下面将编制程序的一些基本公式予以介绍。

3 管程的压降和传热计算方法

3.1 管程的压降计算公式

热交换器管程的压降分为两部分，第一部分为直管部分压降，第二部分为流体在管箱部分转弯时的压降。

直管部分的压降，可由Fanning公式来计算：

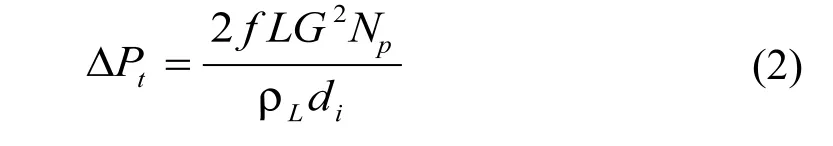
式中的摩擦系数可由Churchill[11]开发的单一的适用于所有Re数范围的公式：

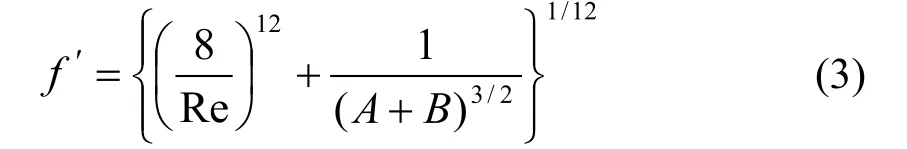
式中：

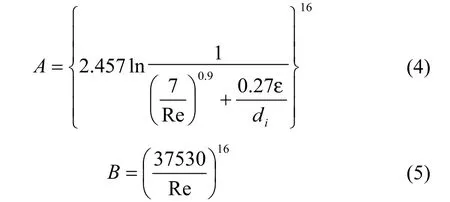
式（2）中的Fanning摩擦系数f = 2f ′。

管箱转弯的压力损失由下式粗略的估计：

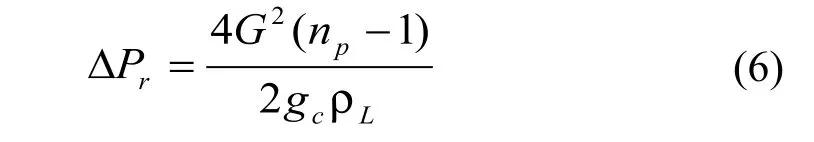
3.2 管程的传热计算

管内的传热系数：

Re < 2100 时采用Hausen[4]的公式：

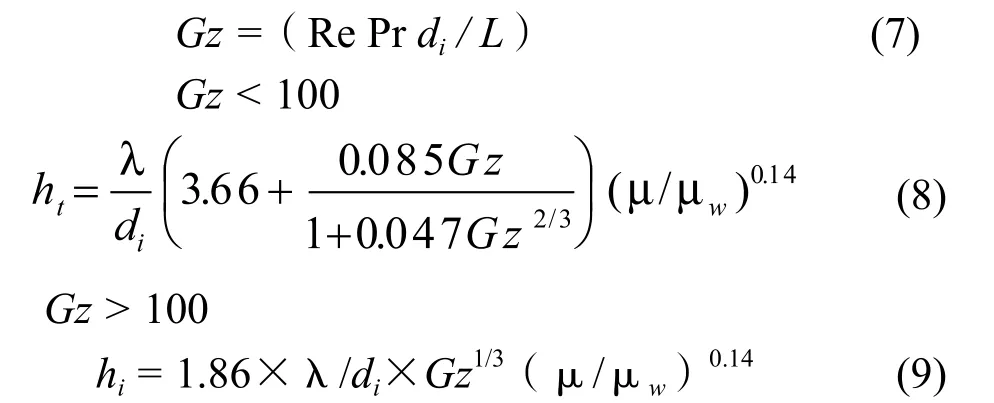
2100< Re<10000 时，采用Hausen[4]公式：

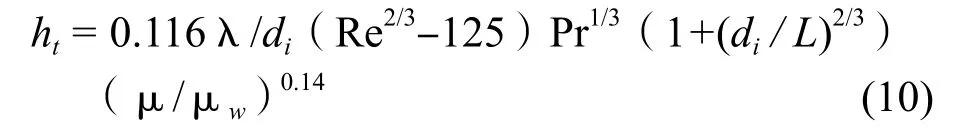
Re > 10000 时，采用Colburn[5]公式：

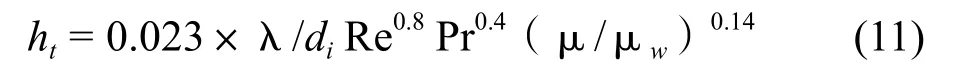
对于高粘性的液体可采用Sieder & Tate[12]的公式：

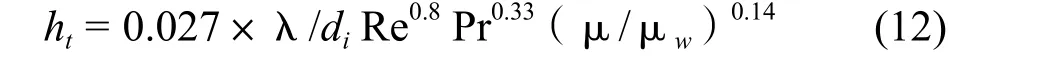
4 壳程的传热和压降计算

壳程的传热计算，齐福来[10]在其文章中已经作了全面地叙述，这里就不重复了，仅以公式的形式罗列出来。而压降的计算在文章中未涉及，在这里予以介绍。

4.1 壳程的传热计算

4.1.1 Kern[7]的方法

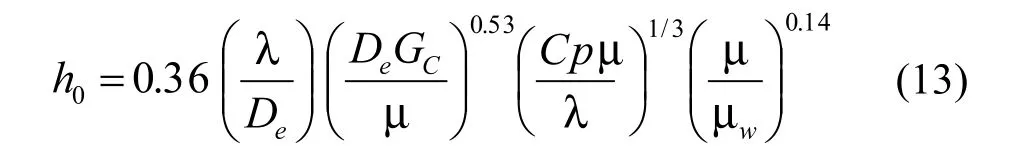
对于三角形配置的管束：

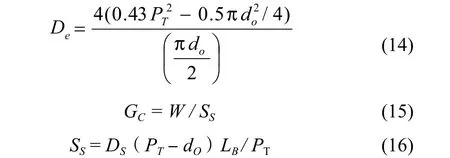
式（13）适用于折流板缺口为25%的情况，其它缺口情况可按下式计算：

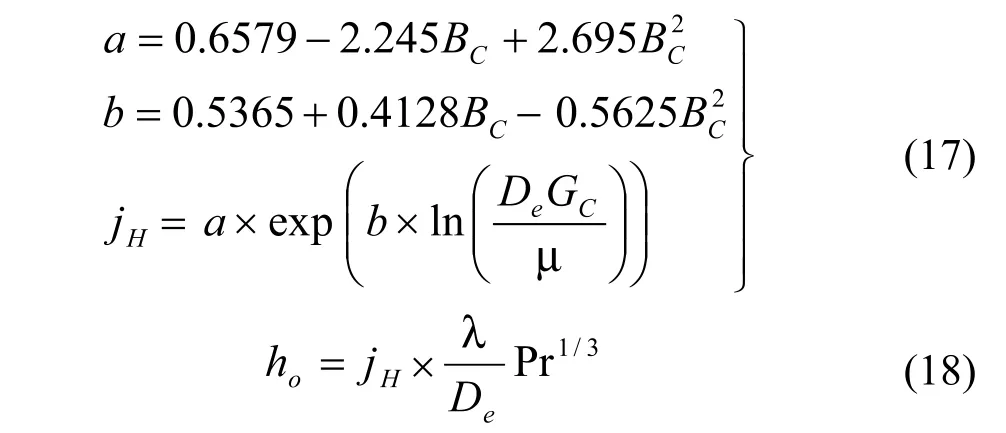
4.1.2 Bell-Delaware[7]法

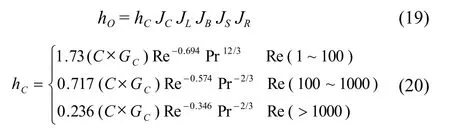
JC－圆缺窗口流体流动的影响；

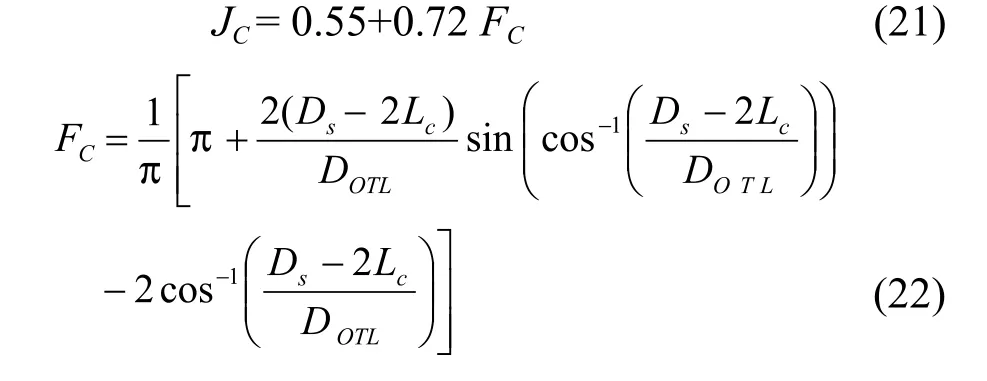
JL－折流板泄露的影响；

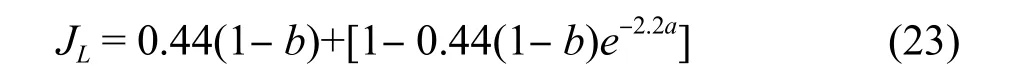
JB－管束旁路的影响；

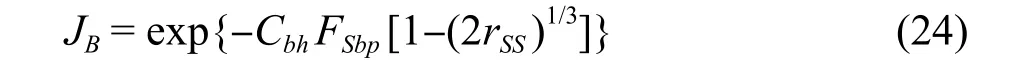
JS－不等距近出口换热器板间距的影响；

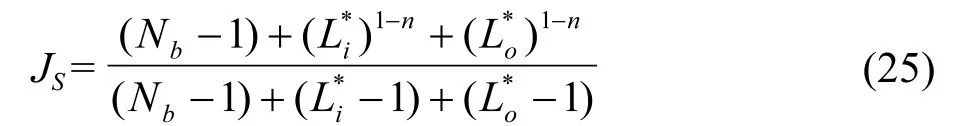
JR－是流体在壳程滞流的影响；

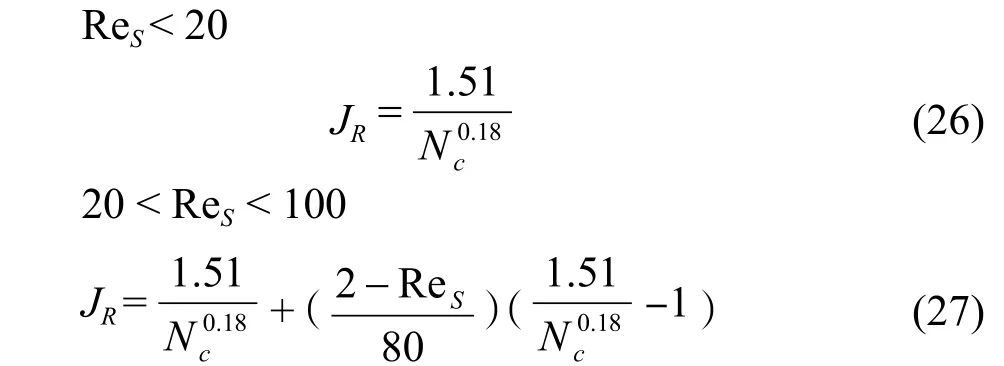
4.1.3 Wills-Johnston[9]流路分析法

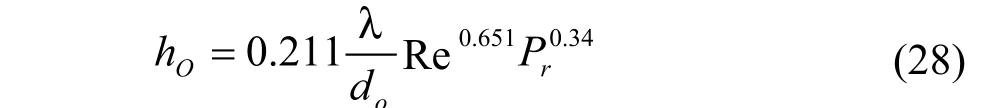
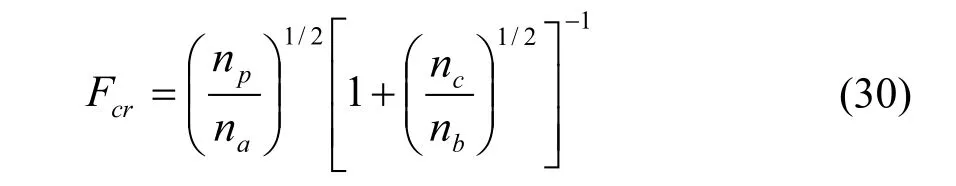
计算FCR是一个迭代过程如下图：

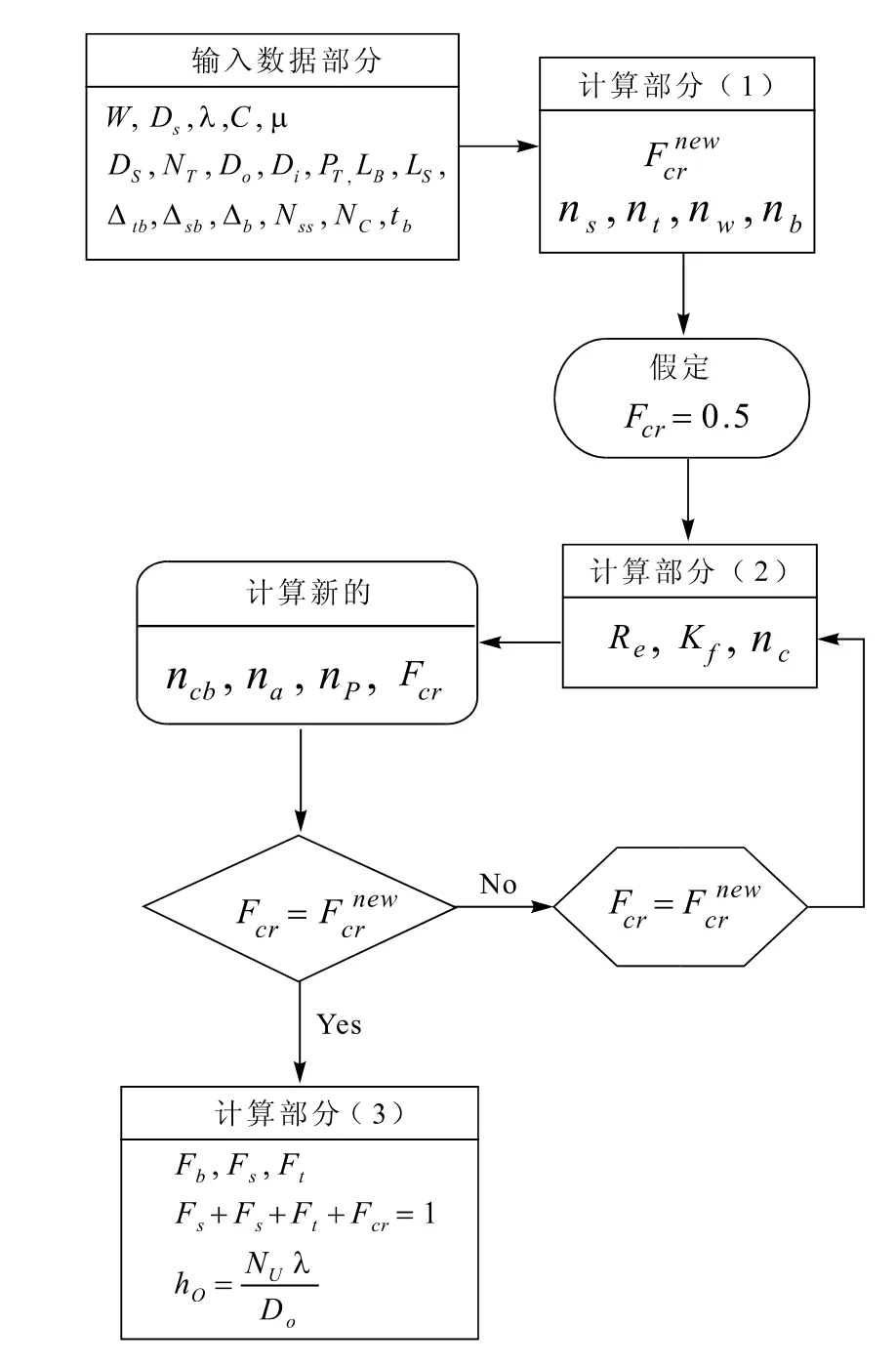
图1 FCR迭代求取图

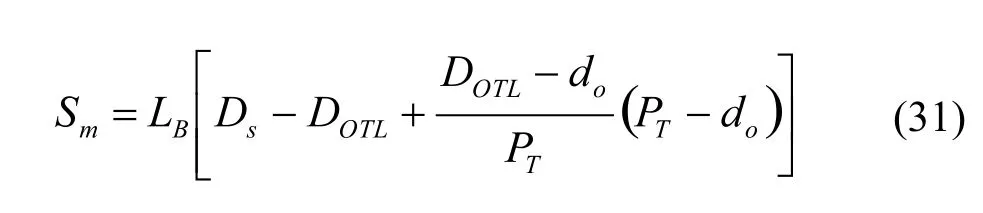
4.2 壳程的压降计算

4.2.1 Kern的方法

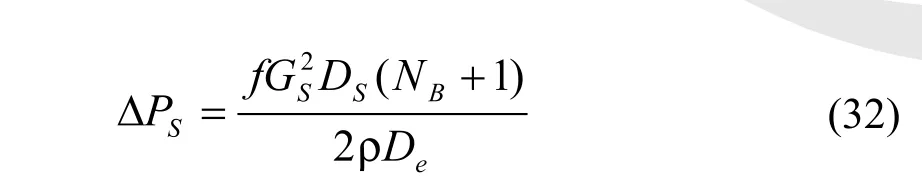
式中：De和公式（14）相同，摩擦系数f由下式计算；

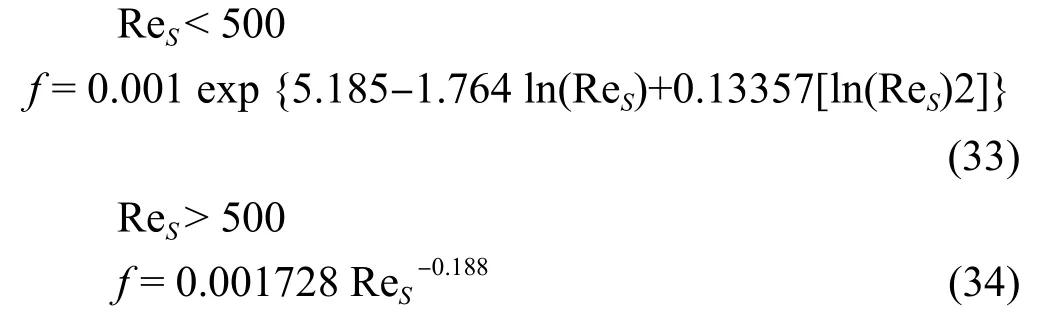
4.2.2 Bell-Delaware 法

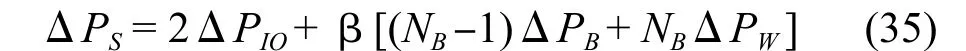
式中：

式中：

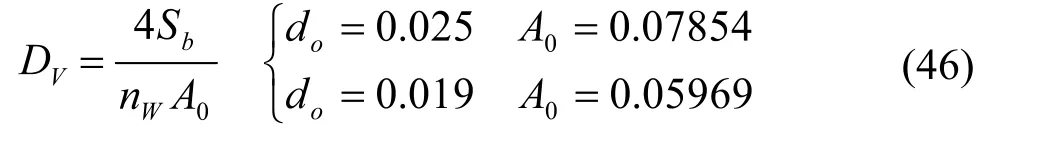
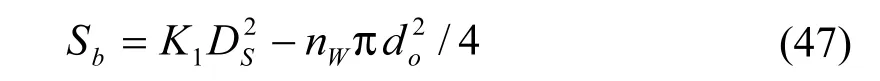
式中K1与折流板的缺口值有关：

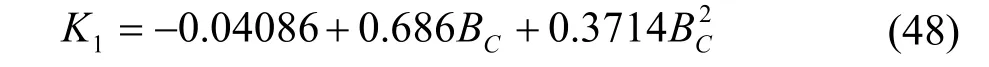
4.2.3 Wills-Jonhston方法

按照该法，在前面传热部分已经对于压降有个交代，因为，此法的传热部分研究就是按照流动的压降平衡原理进行的。因此，计算压降的公式为：

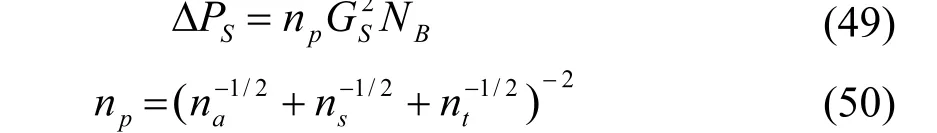
式中na，ns，nt的求法可参阅文献[10]。

5 本程序的选择项与结果以及举例

5.1 本程序的选择项

（1）我国标准，TEMA 标准；

（2）壳程传热系数和压降的计算方法：

①Kern 方法

②Bell–Delawar 方法

③Wills-Johnston流路分析法

（3）管径φ19×2 和 φ25×2.5；

（4）管程的选择。

5.2 本程序的计算结果为两方面

（1）按照使用者选择的壳程计算方法得到的计算结果挑选最大的热负荷的热交换器尺寸予以显示；

（2）将满足使用者要求的所有计算的热交换器尺寸以列表的形式罗列出来以作使用者的研究。在该表中罗列了三种壳程计算方法对每一个尺寸的热交换器计算结果。

5.3 举例说明软件的应用

例题：采用尾花英朗著作[13]的例题，该题是用水冷却API 40°的煤油，从140℃ 冷却到40℃，水由30℃温升至40℃。煤油走壳程。根据温度决定各物料的物理性质如下：

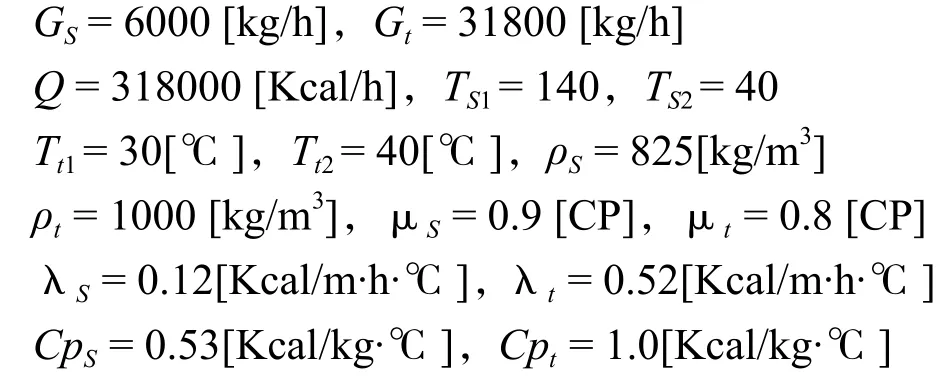
压力限制：

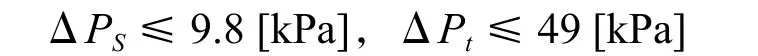
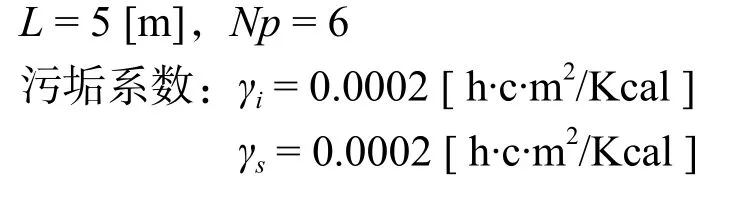
管长限制：按照以上条件打开该软件填写各数值：进入介绍屏幕图2。

图2 介绍屏幕

图3 填写选择项屏幕

在该屏幕内依据题意要求填写以上内容。然后打开‘物料热交换的条件’屏幕图4。

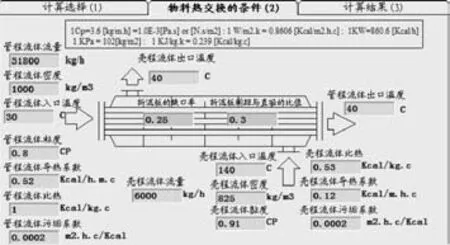
图4 填写物料热交换的条件

按题要求填写各项。然后打开‘计算结果’屏幕。看图5。

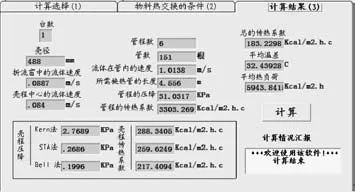
图5 计算结果屏幕

打开该屏幕后直接揿‘计算’按钮就看到计算的结果，该结果是在计算的结果中传热效率最好的一个热交换器。要看所有的计算结果就打开‘计算结果列表框’屏幕图6。

该计算已经计算了12个结果，壳体直径从488[mm]到1067[mm]。在该列表中记载了各种方法的计算结果，以供设计者选择。

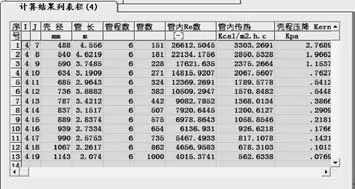
图6 计算结果列表框

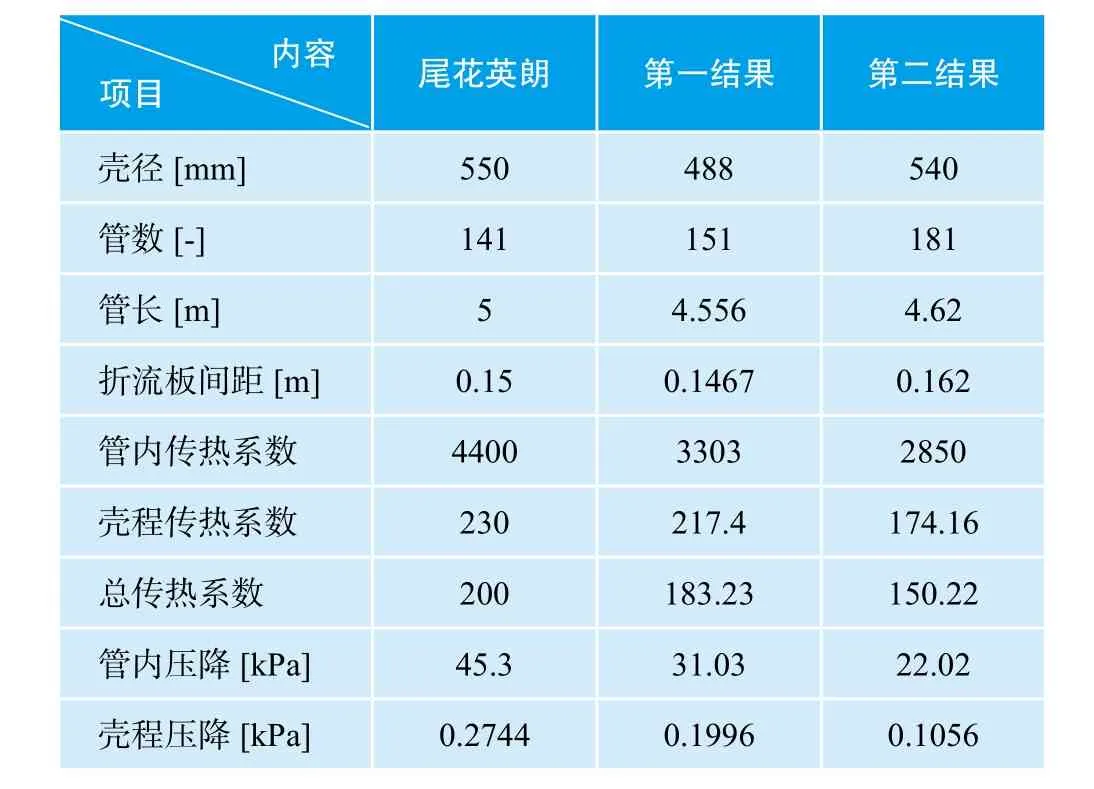
表1 计算结果比较

假如不按照原文的要求选择管程为六程时，其计算结果如下：

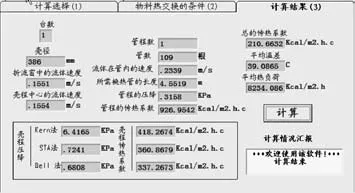
图7 不固定管程数时的计算结果

从计算结果来看不固定管程数得到的结果更经济。

符 号 说 明

BC—折流板的缺口值，[-]；

Cp—流体比热，[kcal/kg·C]；

di—管子的内径，[m]；

do—管子外径，[m]；

De—当量壳径，[m]；

DS—壳径，[m]；

DS′ —据壳程中心最近的管排处的壳径；[m]；

DV—折流板圆缺部分留到的当量直径；[m]；

DOTL—管束的外径，[m]；

FBP—壳径与管束之间的间隙流动面积Sd与错流流动面积SC之比；

f —摩擦系数；

G —流体在管内的流率，[kg/m2·s]；

GC—进中心线处的流体流量，[kg/m2·s]；

GS—壳程的流体流量，[kg/s]；

g —重力加速度，9.8[m/s2]；

h —壳程传热系数，[Kcal/h·m2·C]；

L —管长，[m]；

LB—折流板间距，[m]；

MT—总的壳程流体流量，[kg/s]；

nC—最接近壳程中心线处的管数，[-]；

nW—折流板圆缺口处的管数，[-]；

na，nS，nt，nP—Wills-Johnston方法的流量系数；

NB—折流板数目，[-]；

NC—折流板端之间的管排数，[-]；

Np—管程数；

NS—旁流密封条的数目，[-]；

NW—折流板缺口处的管排数；

PT—管心距，[m]；

ΔPB—折流板之间流动压降，[kPa]；

ΔPIO—管板与折流板之间流动压降，[kPa]；

ΔPS— 壳程的压降，[kPa]；

ΔPT— 管程的压降，[kPa]；

ΔPW—流过折流板缺口的压降，[kPa]；

SC—相同于Sm，错流流动面积，[m2]；

Sb—折流板圆缺部分的流动面积，[m2]；

SS—Kern的壳程进中心线处的流动面积，[m2]；

Sm—Bell 和Wills 法计算的壳程中心线处的流动面积，[m2]；

Vb— Vb= GS/Gb，

VC— VC= GS/GC，

VZ—几何平均流速， VZ=（VCVb）0.5；

W — 壳程流体流量，[kg/s]；

无因次准数：

Gz —格里兹（Graets）准数；

Pe —派克列特准数Pe = diGCp/λ；

Pr —普朗克准数，Pr = Cpμ/λ；

希腊字母：

ρL—液体密度，[kg/m3]；

μ —黏度，[Ns/m2]；

β —壳程流动压降校正系数；

φS—代表黏度随温度的变化项。

[1] Robert H. Perry，Don W. Green，James O.Maloney，Perry’s Chemical Engineer’s Handbook Six.Ed.[M]， p11-14， (1984)

[2] 中国石化集团上海工程有限公司，化工工艺设计手册，第三版[M]，化学工业出版社，P5-353，（2003）

[3] Podder T.K. & Polly G.T.Heat exchanger Design throuth Parameter Plotting，[J] Chem.Eng.Rearch and Design，Vol.74，No.A8，1996

[4] Hausen H.，Vertahrenstechnik，Beih.Z.Ver.Deut. Ing.[J] 4，p91，(1943)

[5] Colburn A.P.，[J]，Trans.Amer. Inst. Chem. Engrs，29. p174，(1933)

[6] Kern D. L. Process Heat Transfer，[M] McGraw-Hill (1950)

[7] Bell K. J. Delaware Method for Shellside design[M]，in Heat Transfer Equipment Design。P145-166 (1988)

[8] Tinker T. ，Shell-side characteristics of shell-and-tube heat exchangers，in Proceedings of General Discussion on Heat Transfer，1951，[R]，Institution of Mechanical Engineers，London，89-116

[9] Wills M. J. N. and Johnston D.，22ndNat.HeatTransfer Conf.，[R] HTD， Am.. Soc .March...Eng.

[10] 齐福来，无相变管壳式换热器壳程传热计算方法的进展，[J]医药工程设计，No. 3，p29， (2002)

[11] Churchill S.W.，Comprehasive correlating Equations for heat，mass and momentum transfer in fully developed flow in smooth tubes，[J] Ind.Eng.Chem. Fundamentals，Vol.16，No.1 (1977)

[12] E.N. Sieder， & G.E.Tate，[J]，Ind.Eng.Chem Vol. 28，p1429 (1936)

[13] 尾花英朗，热交换器设计へソドブック，[M] 笠原洪平，昭和49年，工学图书株式会社