基于dq变换的三相VSR的研究

郑忠玖，李国锋，王宁会

(大连理工大学 电子信息与电气工程学部，辽宁 大连，116024)

引言

高效、无污染地利用电能是目前世界各国普遍关注的问题。传统的二极管整流和相控整流需要电网提供大量的无功功率，同时给电网带来严重的谐波污染，这种严重的谐波污染会影响电网的安全运行和其他电子设备正常工作，低功率因数降低电能的有效利用率。因此，电力系统中无功功率和谐波补偿成为迫切需要解决的问题[1-3]。

PWM整流器具有网侧电流低谐波、单位功率因数、能量双向流动及稳定直流电压输出等优点[4-6]，实现了电能的“绿色变换”。与传统被动补偿方法相比，可以从根本上解决“消除谐波和无功功率”的问题。因此，在电力系统有源滤波、无功补偿、太阳能发电以及交直流传动系统等领域，具有越来越广阔的应用前景。

近些年，符合电能质量标准的新型PWM整流器拓扑和控制策略得到了深入的研究。在所提出的各种拓扑结构中，三相boost型拓扑以其对称电流特性在高功率应用中具有优势，如图1所示。

本文提出了一种双闭环控制策略,即电流内环实现输入电流跟踪控制,电压外环实现输出直流电压控制。结合SVPWM快速算法，使三相PWM整流器具有单位功率因数运行、动态响应速度快、输出直流电压稳定、输入电流THD低等优点。

1 三相PWM整流器数学模型和控制策略

图1 为三相PWM整流器的主电路。图中ea，eb，ec为三相电源相电压；ia，ib，ic为三相线电流；UA，UB，UC为整流器输入电压；L为交流侧电感；R为交流侧等效电阻；CS为直流侧电容；Vdc为直流输出电压；i0为负载电流；RL为负载电阻。

假设：（1）电网电动势为三相对称的纯正弦波；（2）网侧滤波电感L为线性，不考虑饱和的情况；（3）所有元器件均为理想元器件；（4）开关管频率足够高。

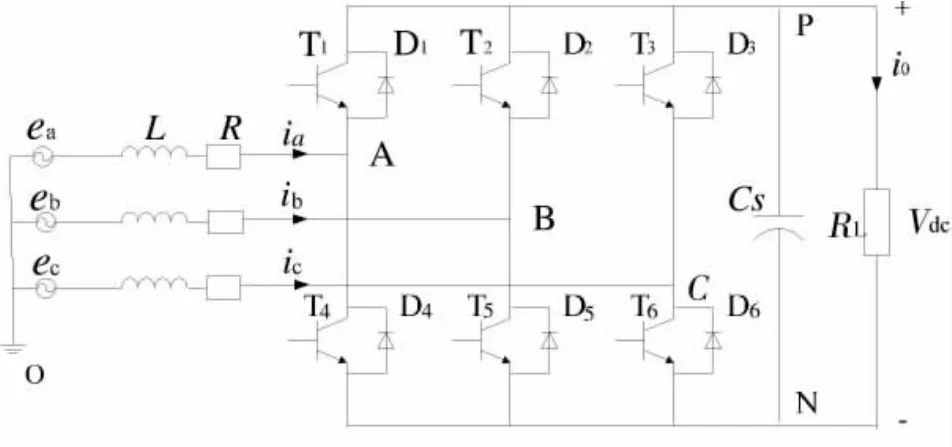
图1 三相PWM整流器主电路

根据基尔霍夫电压定律建立三相PWM整流器电压回路方程，有：

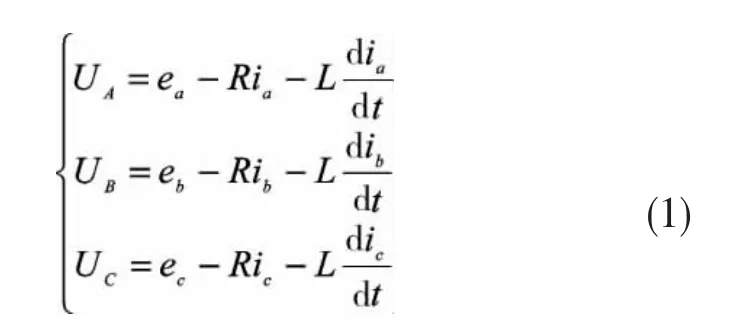
由于在三相静止坐标系下的数学模型交流侧均为时变量，不利于控制系统设计。因此，将三相静止坐标系（a-b-c）下的数学模型通过坐标转换，变成以电网基波频率的同步旋转坐标系（d-q）下的数学模型，可以得到：

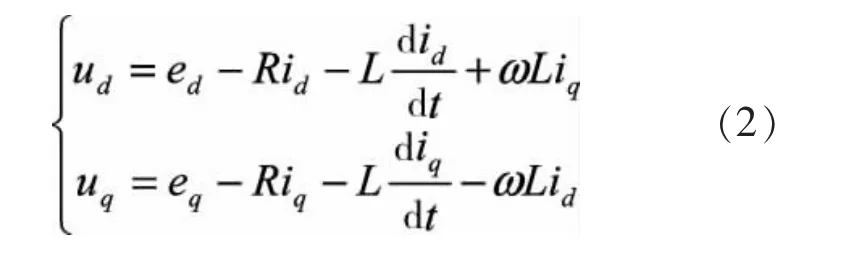
在同步旋转坐标系下，ed，eq为电源电压，id，iq为输入电流，ud，uq为整流器输入电压。可以看出，d，q轴电流除了受整流器输入电压ud，uq影响外，还受到交叉耦合电压 ωLiq，ωLid扰动和电网电压 ud，uq的扰动。由于输入电流存在耦合，因此采用前馈解耦实现由ud，uq分别独立控制两相电流。此时有：

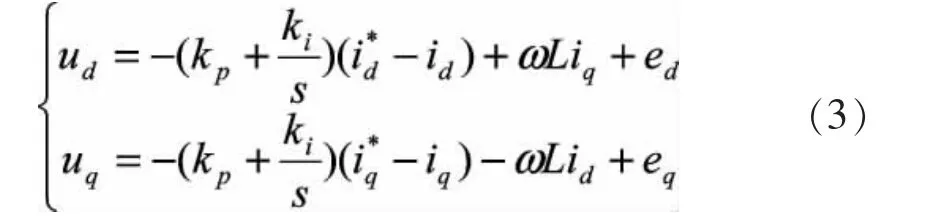
控制框图如图2所示。

2 空间矢量调制的快速算法

空间矢量调制是一种先进而复杂的控制方式，适用于DC-AC交流电机控制，由于PWM变换器能量的双向流动性，同样适用于PWM整流器中。整流器交流输入端的相电压可视作直流侧电压在三组桥臂开关管处于不同开关状态而得。每个桥臂有两种状态，上桥臂导通时为“1”状态，下桥臂导通时为“0”状态。由于三组桥臂共有8种状态，因此电压空间矢量共有 8 种基本工作状态 U0（100），U60（110），U120（010），U180（011），U240（001），U300（101），U000（000），U111（111），其中 U0～U300是非零矢量，U000和U111是零矢量，图3为基本空间矢量分布图。为了使输入电流相位跟踪电压相位和输出稳定直流电压，采用dq坐标系下的双闭环控制方法得到整流器输入侧的指令电压Uref，再根据Uref得到SVPWM驱动波形。

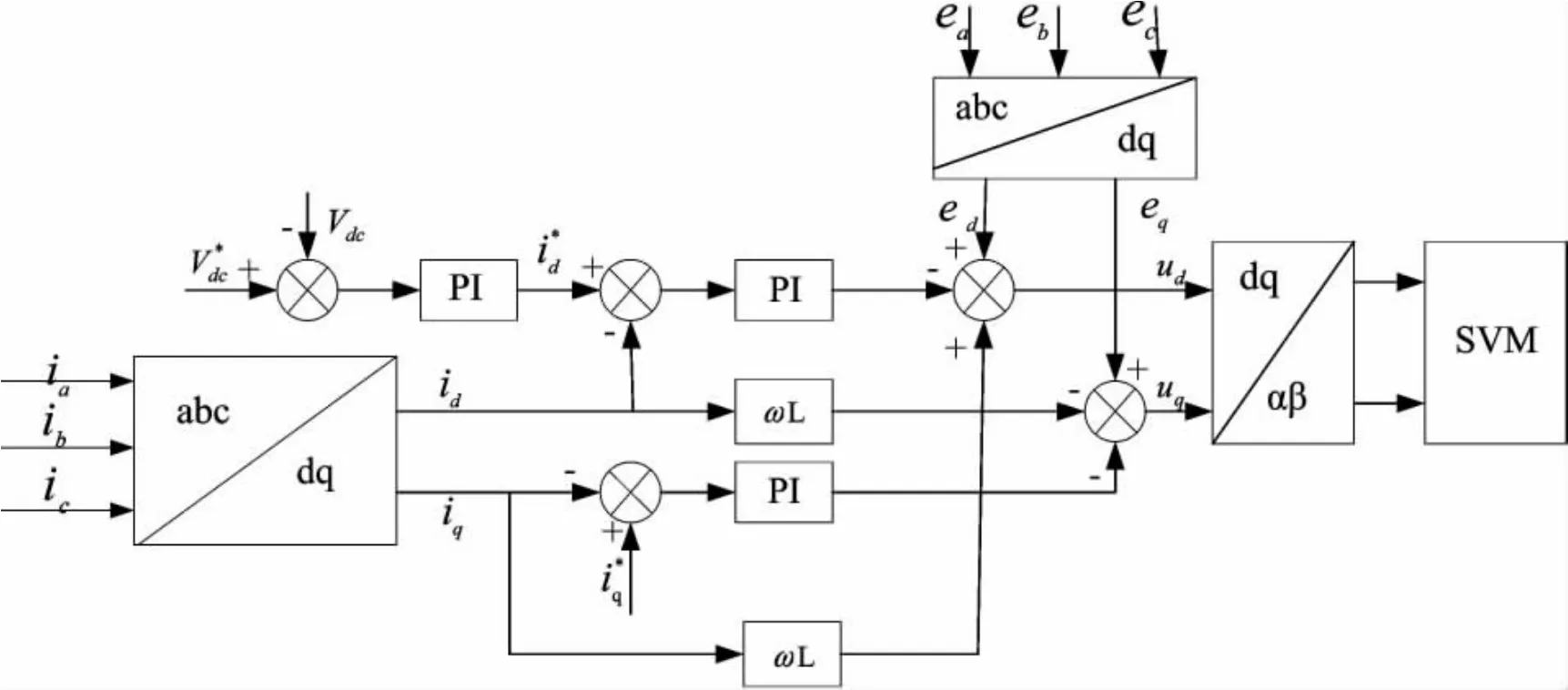
图2 双闭环控制原理图

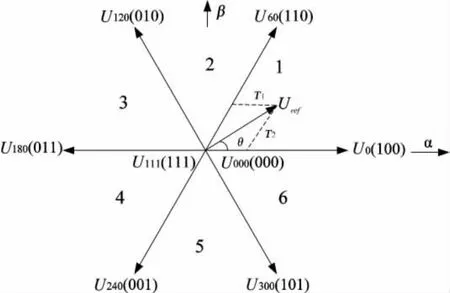
图3 基本空间矢量

图3 中，需要由tanθ确定指令电压Uref在的角度，再通过反正切、正弦函数求出基本空间矢量作用的时间T1，T2。以上非线性运算在定点DSP中是很难达到快速、高精度的计算。本文提出的空间矢量算法将以上运算转化为线性运算，提高的运算速度和计算精度。

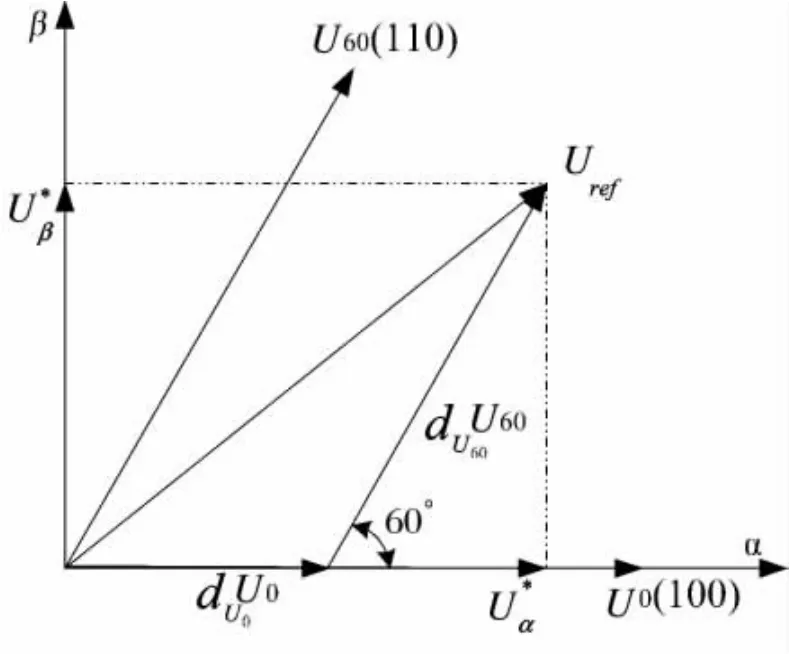
图4 扇区1中指令电压矢量合成

2.1 指令电压所在扇区的判断方法

为了确定指令电压Uref所在扇区，我们将Uref在两相静止坐标系中的分量U*α，U*β进行CLARKE变换。

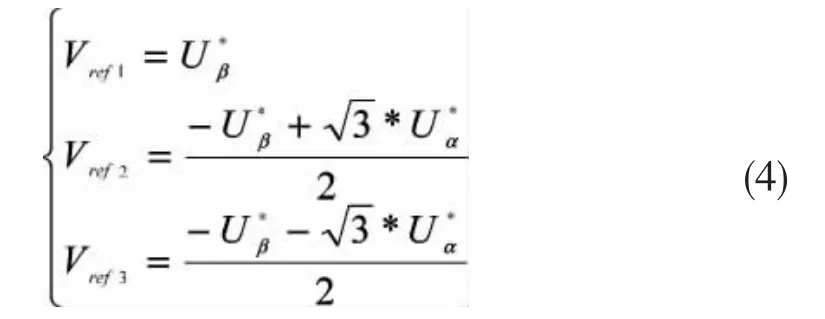
当 Vref1＞0 时，则 a=1，否则 a=0；

当 Vref2＞0 时，则 b=1，否则 b=0；

当 Vref3＞0 时，则 c=1，否则 c=0；

定义变量N=4*c+2*b+a，则变量N与扇区的对应关系如表1。

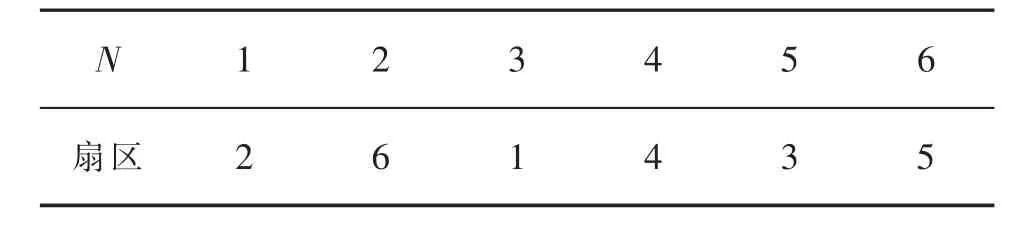
表1 变量N与扇区的对应关系

2.2 调制波占空比计算

图4 为指令电压Uref在第1扇区时，Uref与之对应的 (α,β) 轴分量 U*α，U*β以及基本空间矢量 U0和U60的对应关系。此时，Uref将用U0和U60两个矢量来表示。dU0和dU60分别表示相应矢量在一个周期的占空比。基本空间矢量的幅值为，我们取相对于最大相电压对基本空间矢量进行标幺，则基本空间矢量的幅值变为，即U*β表示指令电压Uref相对于最大相电压标幺后的(α,β)轴分量，于是有：

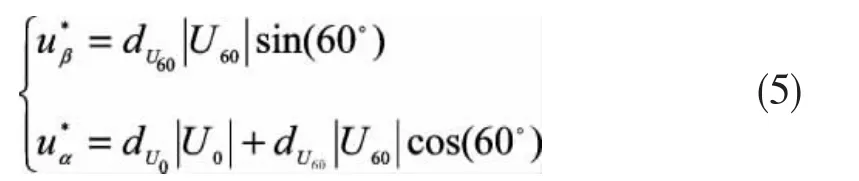
占空比 dU0，dU60为：

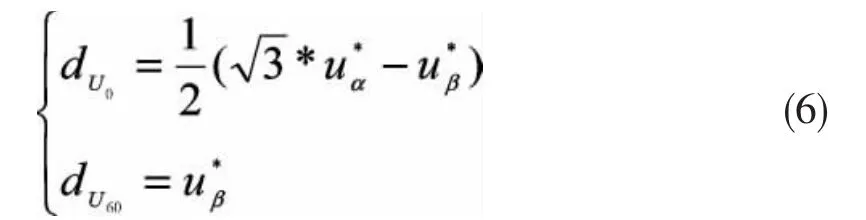
同理，当指令电压Uref在其他扇区时，相应矢量的占空比可以获得，通过分析，得到以下关系式：

不同扇区基本空间矢量占空比值（duk,duk+60）与(dx,dy,dz)的对应关系如表2所示。根据指令电压Uref计算得到占空比信息，从而得到相应的SVPWM控制信号。

表2 不同扇区(duk,duk+60)与(dx,dy,dz)的对应关系

通过上面的介绍，我们可以看到，本文给出的SVPWM快速算法避免的非线性运算，能够提高软件的计算速度和精度。

3 系统仿真与实验结果

基于上述控制策略和电压空间矢量调制快速算法，本文进行了三相电压型PWM整流器在MATLAB/SIMLINK环境下的系统仿真，如图5所示。系统参数如下：输入相电压e=220 V,频率f=50 Hz，系统功率36 kW,交流侧输入电感L=6 mH，电容Cs=4 700 μF，R=20 Ω，系统工作频率 fs=5 kHz。

系统控制部分由电流内环和电压外环组成，电流内环实现电流相位跟踪电压相位，使整流器具有快速的动态响应。电压外环通过PI调节，得到电流环的给定值，同时保证整流器输出稳定的直流电压。控制上采用电网电压定向，使同步旋转的三相电网电压空间矢量为ud，三相网侧电流空间矢量为id（iq=0）。

当系统稳定运行时，输入电流近似正弦波，相位相差2π/3，三相输入基本平衡，仿真波形如图6所示。图7给出了A相输入电压和输入电流的仿真波形，可以看到输入电流相位跟随电压相位，实现单位功率因数运行。图8为直流输出电压的仿真波

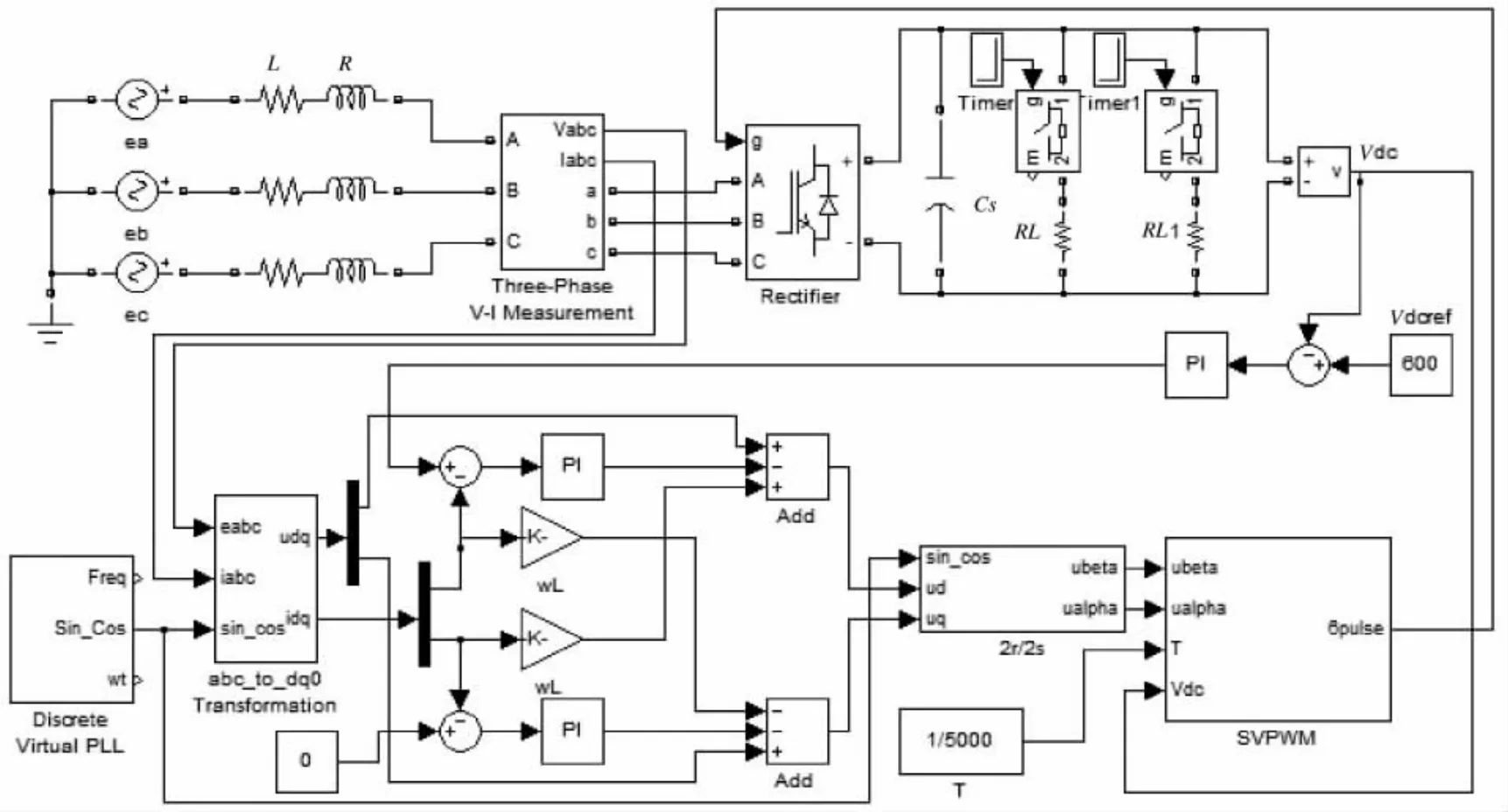
图5 三相电压型PWM整流器系统仿真模型

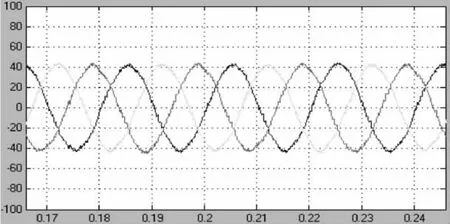
图6 三相输入电流的仿真波形

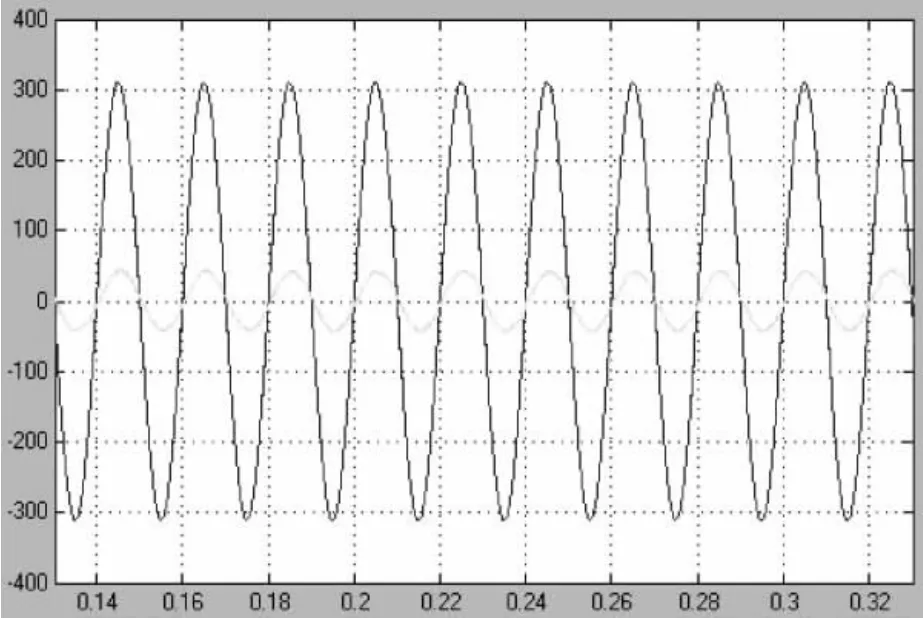
图7 A相输入电压和电流的仿真波形

形，此时，PWM整流器输出稳定的600 V直流电压，整流器开始运行0.05 s后，电压达到设定值，且稳定输出。

为了测试系统的动态性能，在系统稳定运行后0.25 s时，将负载电阻由20 Ω突变为10 Ω。图9和图10分别是负载变化时，A相输入电压、电流波形和直流输出波形，可以看到系统经过0.05 s的时间，重新恢复稳定，输入电流变为原来的2倍，直流电压继续跟踪设定值，整个系统动态性能良好。

根据仿真实验，我们在实验室进行了三相PWM整流器实验样机的研制，硬件系统设计采用了三菱公司的IPM(pm150cla120)，采样调理电路采用LEM公司的电压、电流传感器，辅助电源使用上海嘉尚电子的IPM供电电源和驱动模块，系统核心控制器采用了TI公司的TMS320L2812处理器。软件系统主要由AD采样、坐标转换、dq变换控制、PI调节器和采用软件法实现的空间矢量算法，以上控制程序在定时器1下溢中断服务子程序中完成，实现对系统的周期性控制。

实验参数如下：三相输入相电压E=110 V，输入电感 L=8 mH，直流侧电容Cs=3 300 μF，直流输出电压Vdc=320 V,负载电阻RL为=30 Ω，输出功率P=3.4 kW，系统工作频率fs=10 kHz。图11为三相PWM整流器A相电压、电流和直流输出电压波形，实验结果证明，三相输入电流跟踪电压相位，输入电流为正弦波，直流输出稳定。利用HIOKI3166型电力计对样机进行测量，三相功率因数为0.99以上，输入电流谐波含量THD<5%。

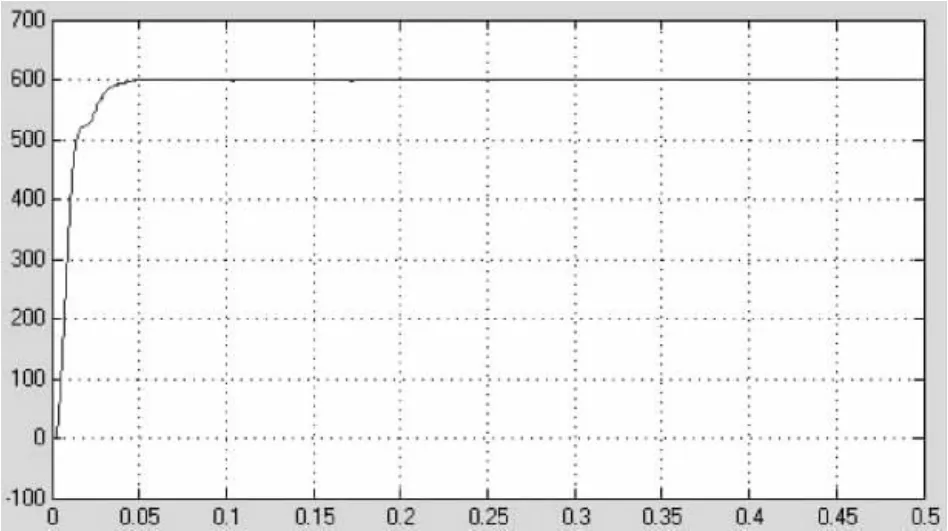
图8 输出直流电压的仿真波形

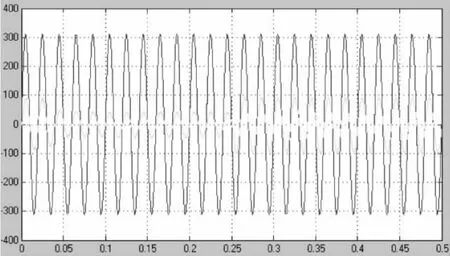
图9 A相输入电压和电流的仿真波形（负载由20 Ω突变为 10 Ω）

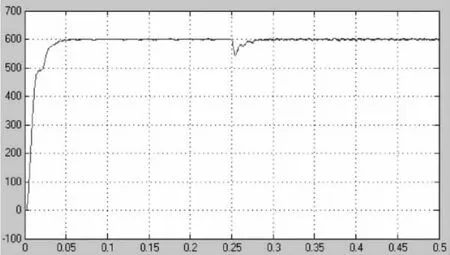
图10 输出直流电压的仿真波形（负载由20 Ω突变为10 Ω）

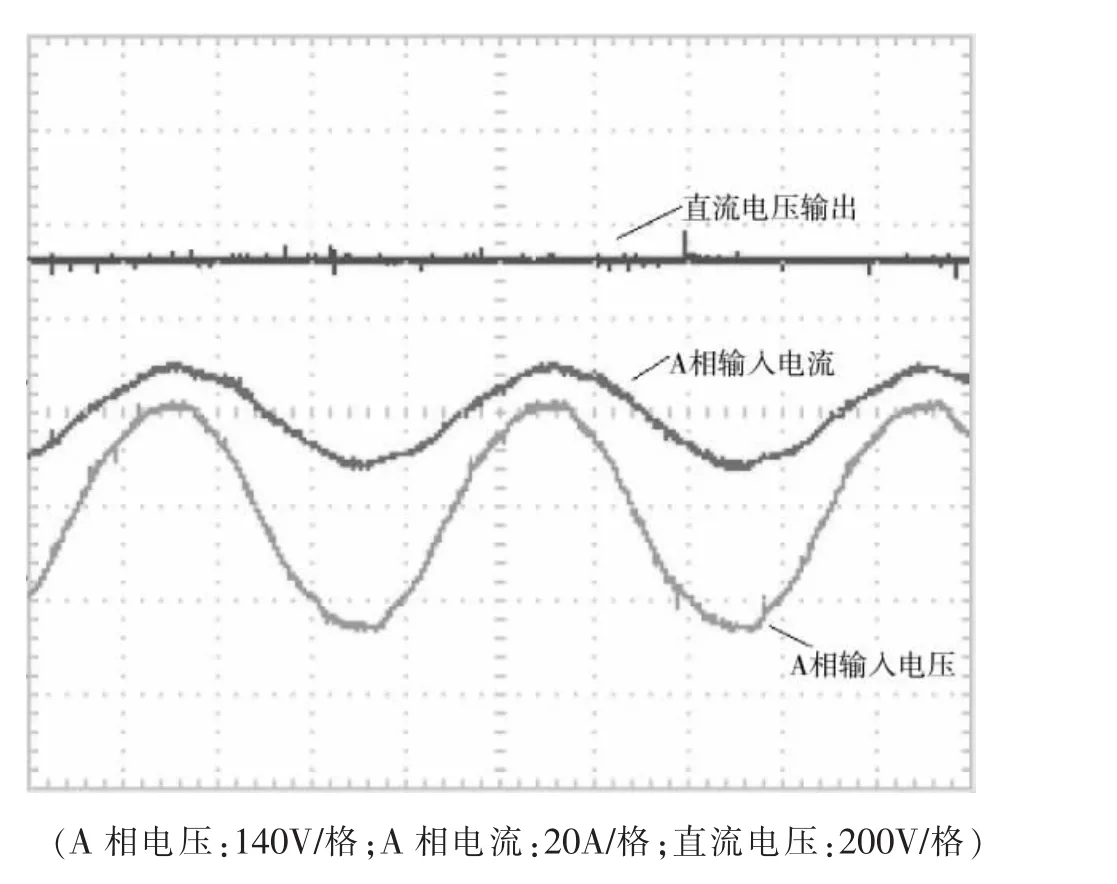
图11 三相PWM整流器A相电压、电流和输出直流电压实验波形

4 结论

本文通过对PWM整流器在d-q坐标系下数学模型的推导和分析，提出了一种两相解耦的d-q坐标系下的双闭环控制方法。并应用了SVPWM快速算法，该算法无需任何三角函数运算，计算简单。在MATLAB/SIMULINK中建立了三相PWM整流器的仿真模型，并在实验室中进行了3.4 kW实验样机的研制，通过仿真和实验结果可知，本文提出的PWM整流器实现了单位功率运行，输入电流畸变率低，输出直流电压稳定。

[1] Singh B，Singh B N,Chandra A,Al-Haddad K,Pandey A,Kothari D P.A review of three-phase improved power quality AC-DC converters.IEEE Trans.Ind.Electron.2004，51（3）：641-660.

[2] 伍小杰，罗悦华，乔树通.三相电压型PWM整流器控制技术综述[J].电工技术学报,2005,20(12):7-12.

[3] Liuchen Chang and Kojabadi H M.Review of interconnection standards for distributed power generation.Power Engineering 2002 Large Engineering Systems Conference on.LESCOPE,pp.36-40,June 2002.

[4] 王久和，李华德，王立明.电压型PWM整流器直接功率控制系统[J].中国电机工程学报，2006,26(18):54-60.

[5] Batista F A B and Barbi I.Space vector modulation applied to three-phase three-switch two-level unidirectional PWM rectifier.IEEE Trans.on Power Electron.vol.22,pp.2245-2252,Nov.2007.

[6] Prodanovic M and Green T C.Control and filter design of three-phase inverters for high power quality grid connection.IEEE Trans.on Power Electron.vol.18,pp.373-380,Jan.2003.