作战机器人折反射全景视觉侦察技术

马子领，王建中

(1.北京理工大学 爆炸科学与技术国家重点实验室，北京100081;2.华北水利水电学院 机械学院，河南 郑州450011)

作战机器人主要用于战场侦察、巡逻和攻击，侦察系统是其重要组成部分，目前侦察系统大多利用单摄像机+云台旋转、多摄像机+图像拼接以及鱼眼透镜+普通摄像机等。然而这些方法由于图像处理计算量太大导致实时性较差。

全景成像技术由于能获得360°的大视场，在机器人、计算机视觉和虚拟现实等领域发挥重要的作用，图像拼接［1］、鱼眼透镜［2］和折反射透镜［3］是实现全景成像的主要方法。图像拼接方法原始数据量大，拼接算法复杂，一般只能实现非实时的柱面全景成像。鱼眼镜头方法要得到无畸变的全景图像必须经过校正运算，实时性差，而且系统昂贵。折反射成像方法由于没有扫描部件、设计柔性好、成本低、无拼接直接获得360°大视场等［4］优点，近年来获得较快发展。

本文从城市作战环境的实际需求出发，研究基于折反射成像的作战机器人全景侦察技术。在满足实时性的前提下，使目标场景投影到CCD 成像面时占有的有效像素尽可能多。实现这个目标有2 种途径: 1)选用大尺寸高像素CCD 摄像机，2)通过折反射成像系统设计充分利用CCD 摄像机的有效像素。由于生产工艺水平所限，CCD 尺寸不可能太大，且越大成本越高;另外像素越高，数据量就越大，会导致后期处理难度加大。为此本文研究第2 个途径。

1 系统建模

综合考虑应用需求和各种光学折反射镜面的成像特点［5］，本文选用双曲面形的光学折反射镜面。系统由一个双曲面反射镜和一个普通摄像机组成，其简化模型如图1所示。由于双曲面折反射全景成像系统满足单视点成像条件［6-7］，将摄像机透视中心置于双曲面反射镜的焦点F2，则会聚于另一焦点F1的光线经双曲面反射后必会聚于摄像机透视中心，焦点F1称为全景系统的透视中心。

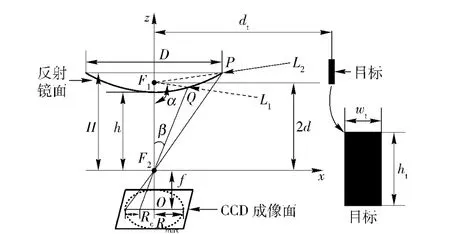
图1 成像系统示意图Fig.1 Sketch of imaging system

设双曲面反射镜的宽度为D，反射镜上边缘距摄像机透视中心的高度为H，双曲面两焦点的距离为2d，入射光线L1与z 轴负方向的夹角为α( 亦即系统视场角)，入射光线L1经反射镜反射后的光线与z轴的夹角为β( 亦即摄像机视场角)，入射光线L2经过反射镜面的最边缘点P( D/2，H)、其亦决定了系统最大视场角αmax和摄像机最大视场角βmax，摄像机的焦距为f，Rmax为CCD 成像面有效像素上最大圆的半径、亦即入射光线L2在CCD 成像面上的投影点到CCD 成像面中心( O)的距离。

由于双曲面反射镜面为旋转对称结构，只须在xF2z 平面内进行分析。设双曲线方程为

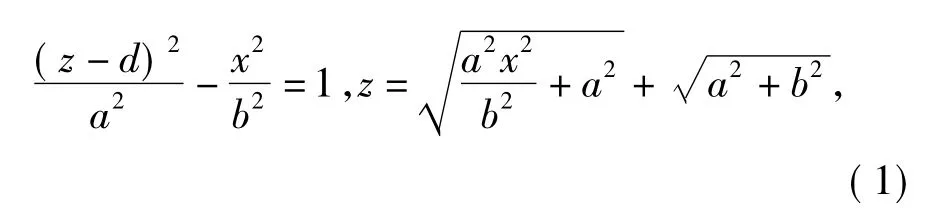
最边缘点P 的坐标为( D/2，H)，即

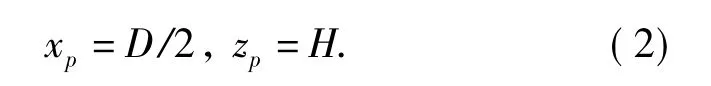
由图1可知

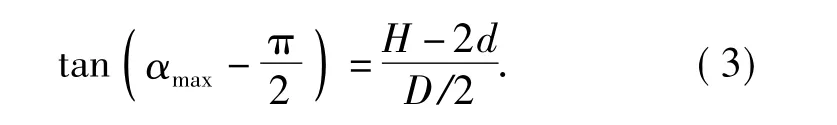
由(1)式～(3)式可得

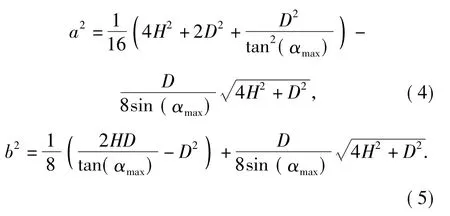
在αmax处，摄像机有最大视场角βmax，且有

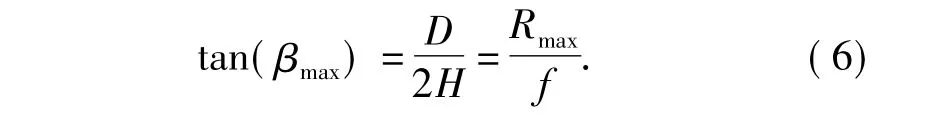
设入射角为α 的光线与双曲面的交点为Q( xq，zq)，则

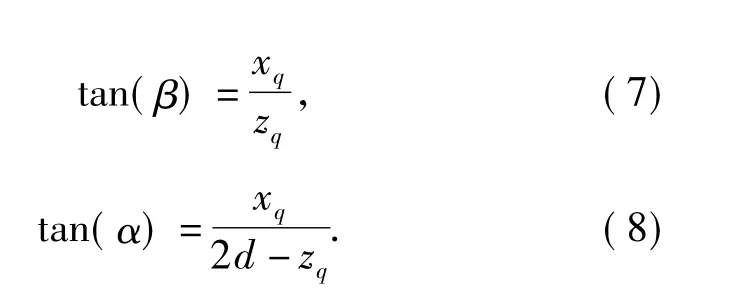
由(7)式、(8)式可得

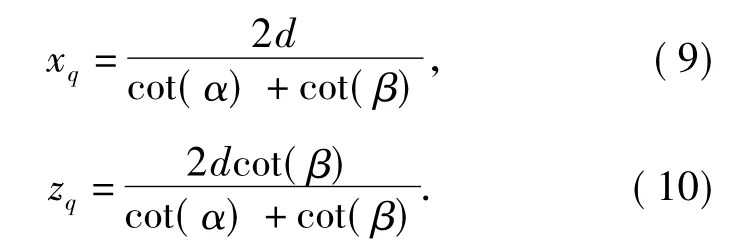
联合(1)式、(9)式、(10)式可得

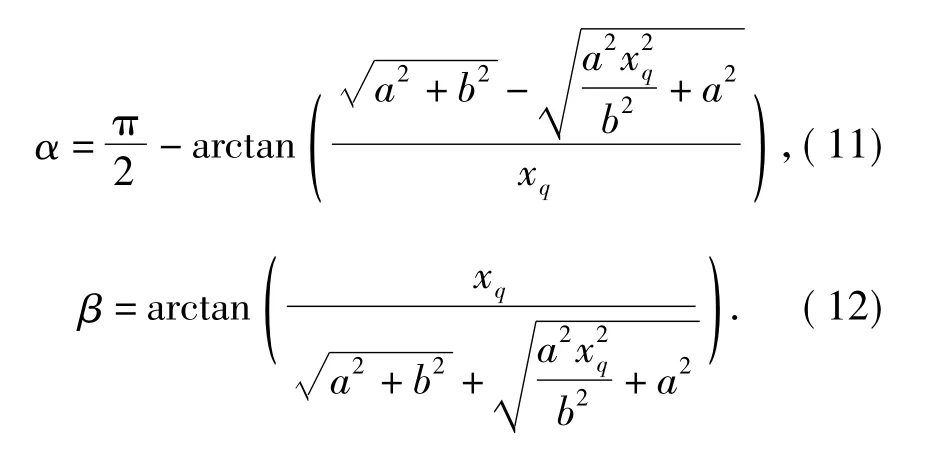
联合(11)式、(12)式可得

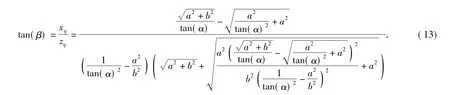
2 观测距离与分辨率

设直立目标( 如图1所示)的高度为ht、宽度为wt，至镜头的距离为dt，目标下边缘与焦点F1相平行，即目标一端的视场角为α1=90°.假定dt远大于目标的高度和宽度，则目标所占的系统视场角范围为Δα，可由

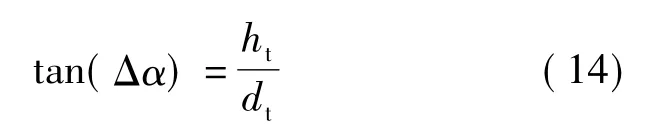
计算，于是可得目标上边缘处的视场角

根据(13)式可计算出目标所占的相应的摄像机视场角范围Δβ，即［β1，β2］( β2、β1分别为目标上、下边缘处光线经反射镜反射后与z 轴的夹角)，从而可计算目标所成像的高度h't和宽度w't( 如图2所示，2 个圆环中间的环带是图1所示系统生成圆环状全景图的有效区域，区域ABCD 即为图1中目标所成的像为目标的上边缘，为目标的下边缘到的距离即为高度h't，到的距离即为宽度w't)，由图1所示的反射光线、目标成像点到CCD 成像面中心的距离、焦距之间的关系易知

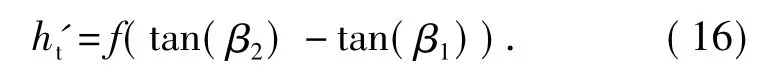
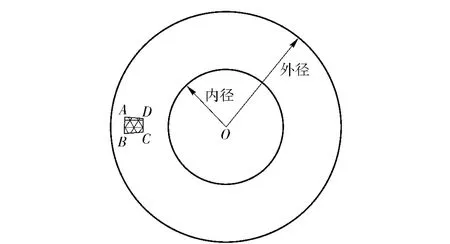
图2 目标成像示意图Fig.2 Sketch of target imaging

根据几何比例关系，显然，目标的宽度wt在以全景系统的透视中心F1为中心的圆周上所占的比与目标所成像的宽度w't在以CCD 成像面中心( O)为中心的圆周上所占的比相等，另外由于dt远大于目标的高度和宽度，因此可将目标所成的像近似认为高为h't和宽为w't的矩形，则可推导出

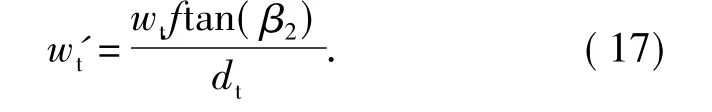
令摄像机CCD 的单位像素大小为U，于是可得目标成像面积所拥有的像素数

同样大小和距离的目标在CCD 成像面上占有的像素数S 越多，目标的分辨率越高。

3 系统参数分析与仿真计算

由于所侦察目标的距离远近不一，故假定能侦察到较远距离的目标，则有效系统视场角集中在90°附近，另外系统视场角在［0°，120°］范围内时反射镜厚度与最大系统视场角接近成线性变化［6］，故设定最大视场角αmax=95°.

选用2/3 英寸靶面的方形CCD 图像传感器，可计算出Rmax=3.77 mm.根据普通摄像机的外形尺寸初选反射镜口径D=50 mm，由( 6)式可知f 和H成正比关系。根据普通定焦镜头的焦距情况，取f在4～75 mm 范围内变化，可得到H 的变化范围约为27～497 mm.欲使系统结构紧凑，H 应小些，因此f 就应选小些。再根据(4)式、(5)式，由αmax、D 及H可得到一组( a，b)值，从而可绘制一族双曲线( 即一族双曲面反射镜面的型线)。分别取f=4，8，12，16，25，75 mm 绘制双曲线，如图3所示，其纵横坐标比例相同。为便于比较各反射镜的形状，对各双曲线的纵坐标做了调整，使它们的两端点重合。

设T 为反射镜的厚度，由图1可知

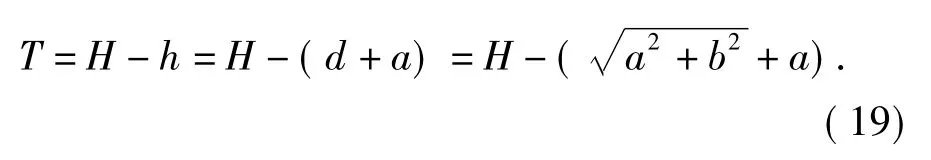
由图3可知，每个f 值对应一条双曲线，也就对应一个T 值，从而得到f 和T 的关系，如图4所示。可见当f 小于20 mm 时，厚度的变化对f 值的影响不大，这意味着镜子的加工误差可以在允许的范围内稍大，从而有效降低加工成本。

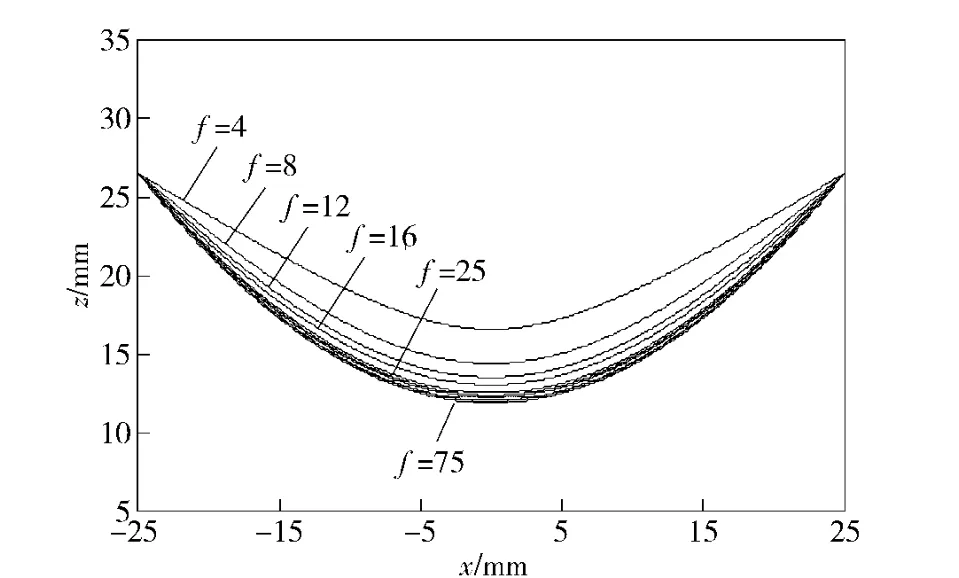
图3 焦距f 取各值时的双曲线Fig.3 Hyperbolic curves with various focus f

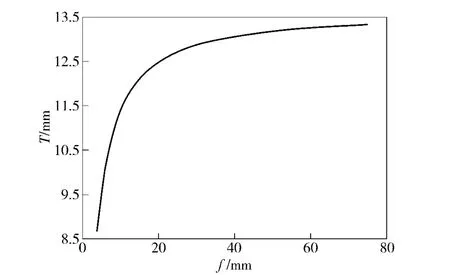
图4 焦距f 和厚度T 的关系Fig.4 Relation between focus f and thickness T

对任一条双曲线，以x 为自变量，由( 11)式、(12)式可得一组( α，β)值，然后以α、β 为横纵坐标绘图，如图5所示。可见f 越小，αmax=90°附近曲线斜率越大，β 变化范围就越大。相应地，在视场角90°附近的目标场景投影到CCD 成像面上时占有的有效像素就越多，于是分辨率就越高，目标也越清晰。

假定有效视场α 的范围为［80°，95°］，对任一f值，由( 11)式可以计算出α=80°时xq的值，再由(12)式可计算出β 的值，令与此时β 相应的CCD成像面上的半径为Rmin，则与有效视场α 相对应的有效像素宽度

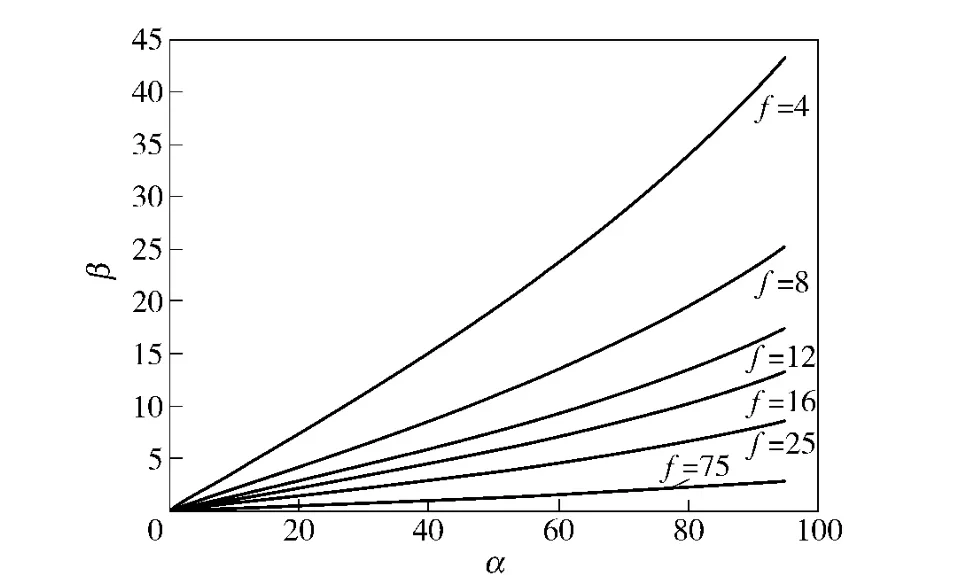
图5 焦距f 取各值时α 和β 的关系Fig.5 Relation between α and β in different focus f

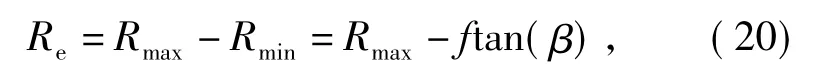
从而得到焦距f 与有效像素宽度Re的关系，如图6所示。可见f 越小，有效像素就越多。

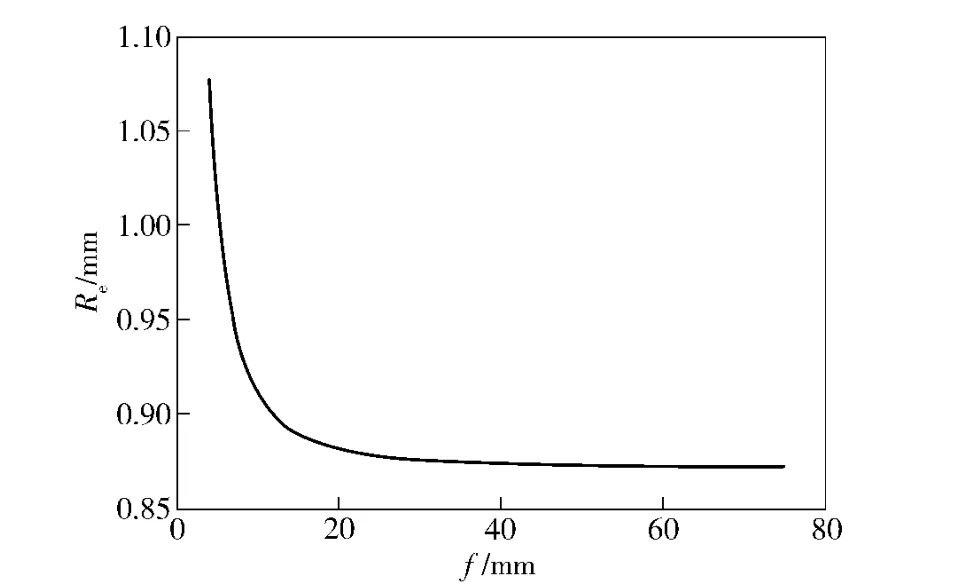
图6 焦距f 与有效像素宽度Re 的关系Fig.6 Relation between focus f and effective pixel width Re

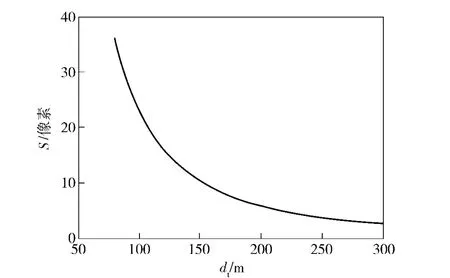
图7 观测距离dt 与分辨率SFig.7 Resolution S vs.distance dt

对任一f 值，由(6)式知D 和H 的比为一定值，将其比例关系式代入(4)式、(5)式可知a、b 都与D成正比，且a 与b 的比也为一定值，再将a、b 关于D的比例关系式代入( 13)式可消去D，于是得出tan( β)只与tan( α)一一对应，而与D 无关，即当f 一定时，D 的变化不改变有效像素宽度Re的大小。因此，反射镜口径D 可根据外形尺寸需要自由选择。

4 实验及分析

选择f=12 mm.假定CCD 的像素大小为6.45 μm×6.45 μm，目标高度为1.7 m，宽度为0.5 m，根据(18)式可得系统的观测距离与分辨率之间的关系，如图7所示。

根据上述假定参数设计的仿真系统获得的全景图如图8所示，图9为其展开后的全景图，图10为图9的局部放大图。对比美国里海大学实验室设计的全景视觉环境感知系统的实验结果( 50 m 远处的人在图像上的大小为16个像素，城市街道环境中的正确识别和跟踪率达90%以上)，本系统对100 m远处所假定大小的目标在CCD 上成24 个像素大小的像( 如图10所示，目标为24 个像素的矩形，其右边是24 个像素大小的人)，因此由图7可知，在较佳图像分辨率和设备分辨率下，该系统能侦察到超过100 m 远的目标。

图8 全景图Fig.8 Panoramic image

图9 展开全景图Fig.9 Unwarped panoramic image

图10 24 个像素大小的人和假定目标Fig.10 Target and people with 24 pixels

5 结论

本文建立了基于双曲面折反射全景成像方式的作战机器人侦察系统模型，通过对模型相关参数的分析和定量参数下的仿真实验，给出了侦察系统设计的参数选择依据。由仿真结果可以看出，当摄像机焦距较小时，系统可以观测更远的目标，这与单独用摄像机观测时焦距越长看得越远刚好相反。最后依据仿真结果确定一具体系统，对一假定的具体目标进行了观测距离与分辨率关系的仿真，并给出了实验结果予以验证，结果表明该系统可以实现对较远距离全景目标的侦察。

References)

［1］ Bao P，Xu D.Panoramic image mosaics via complex wavelet pyramid［C］.Piscataway:IEEE，1998，5:4614-4619.

［2］ Kumler J，Baner M.Fisheye lens designs and their relative proformance［C］.San Diego:SPIE，2000，4093: 360-369.

［3］ Baker S，Nayar S K.A theory of catadioptric image formation［C］.Bombay:IEEE，1998: 35-42.

［4］ 肖潇，杨国光.全景成像技术的现状和进展［J］.光学仪器，2007，29(4):84-89.XIAO Xiao，YANG Guo-guang.A present and development of panoramic imaging technique［J］.Optical Instruments，2007，29(4): 84-89.( in Chinese)

［5］ 丁艳.全方位视觉技术的综述［J］.科技信息，2007，34:564-565.DING Yan.Summarize of omnidirectional vision［J］.Science ＆Technology Information，2007，34:564-565.( in Chinese)

［6］ 曾吉勇，苏显渝.双曲面折反射全景成像系统［J］.光学学报，2003，23(9):1138-1142.ZENG Ji-yong，SU Xian-yu.Hyperboloidal catadioptric omnidirectional imaging system［J］.Acta Optica Sinica，2003，23(9):1138-1142.( in Chinese)

［7］ Baker S，Nayar S K.A theory of single-viewpoint catadioptric image formation［J］.International Jounal of Computer Vision，1999，35(2): 175-196.