关联研究中信息的提取与压缩

郑 勇, 侯燕芳

(1.陕西科技大学图书馆, 陕西 西安 710021;2.陕西省社会科学院, 陕西 西安 710065)

0 引 言

共引分析自诞生以来，其理论和方法逐渐成熟，由于分析结果的客观性，使得它已成为一种可靠实用的情报研究方法.目前共引分析的应用范围还主要集中在情报学、生物、医学、农业等学科领域，尚少见有与工业等第二产业直接挂钩的[1].特别是在陕西省，这方面的应用研究尚处于空白，因此如能将其应用范围扩大到产业领域，研究产业发展与科技人员群体结构特征之间的直接关联，则对于促进某些产业的健康、快速发展将是一件很有意义的工作.

我们已经利用作者同被引分析(ACA)技术[2]完成了对我省典型学科专业的演进研究和典型行业的科技人才群体结构特征的提取方法及地区间的比较研究[3-5].本文将进一步深入地讨论产业发展指标的选取、高维数据集的降维等关联研究中的若干特征之表征问题，并对关联的计算方法进行初步的探讨.

1 产业发展指标的选取与分类

产业和科技人才群体是社会-经济大系统里的两个小“系统”，我们可以分别研究这两个系统，也可以在更广大的范围的大系统中将它们作为两个“子系统”来研究它们之间的关联.要想研究产业发展与科技人才群体结构之间的关联，首先要搞清每个系统中包含有哪些起决定性作用的要素，分别提取系统的特征或表征，确定系统内部和它们之间关联的途径，即可确定系统的结构，然后对于表明这些关联的“链条”上的作用强度进行量化和计算，并作出人文社会科学意义下的诠释.只有全部完成了上述任务，才能说是对关联做了完整的、充分的分析与研究.

在科技人才群体这个系统中，要素即是核心作者.在本课题的研究中，认为核心作者之间是以同被引关系作为关联的途径和链条的.正是通过这种同被引关系构成了一种网状结构，组成了一个“群体”，即所谓的“系统”.关于科技人才群体结构的特征及其提取问题，我们已经做过详细的研究，此处不再重复.这些特征可以被用来研究与产业发展的关联.现在的问题是要考察和提取哪些可以表征产业发展的要素与指标.

在国民经济中，产业通常被划分为第一产业、第二产业和第三产业.第一产业是指农、林、牧、渔业.第二产业是指采矿业、制造业、电力、燃气及水的生产和供应业、建筑业.第三产业是指除第一、二产业以外的其他行业.我们将以第二产业(除了建筑业)的工业企业作为“产业”的代表进行其发展表征与关联研究.国民经济的一些产业的主要经济指标可以从各种统计年鉴等出版物或相关的数据库中找到，但其指标非常庞杂，常给研究工作带来许多困扰，因此需要经过仔细挑选，才能确定对于某项研究所需的要素.

2004年，我国曾开展了第一次全国经济普查，获得了大量翔实、准确的资料.后来，依据这些资料汇编成《中国经济普查年鉴-2004》一书出版.全书共3卷4册，即综合卷、第二产业(上、下册)和第三产业卷，并随书提供光盘载体的数据库.我们拟以此年鉴及其数据库作为最主要的数据源之一，给出数字示例来说明产业发展的表征问题.为了研究产业发展的表征及其与科技人才群体结构特征之间的关联，我们拟截取一个横断面，即对全国31个省、市、自治区(不包括台、港、澳地区)的全部工业企业的主要经济指标进行考察，从中选出与科学研究和技术开发等方面活动的关系比较密切的项目作为对象进行研究.

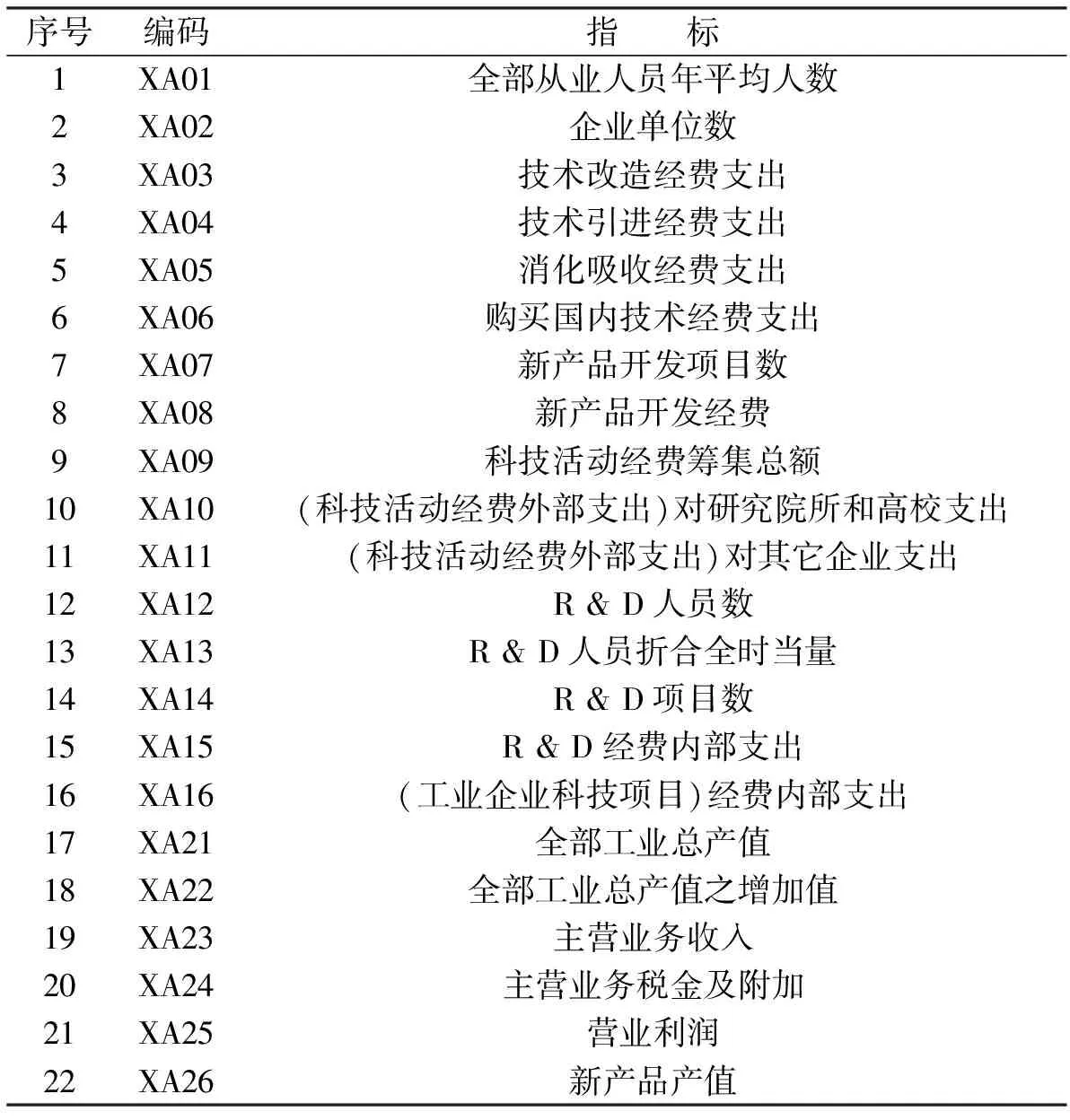
表1 选出的主要经济指标

如果我们进一步地考察产业系统，就会发现其内部的结构是十分复杂的.因此，在选定其要素时不仅要注意其总的数目，而且要注意到它们的类别.这种类别的区分虽然可以借助于多元统计分析的方法，但更多的时候可能需要经济学方面的知识.通常，我们可以把产业的主要经济指标划分为投入项和产出项，分别选取要素以研究变量间的相关关系.经过缜密地考虑和仔细地挑选，我们选取16个投入项，同时选出对于经济效益比较重要的6个产出项作为对象进行研究(表1).

一般来讲，如果“类”划分得正确，那么同一类样品的类内平均距离应当比较小，而类间的平均距离则应当较大.

我们按文献[4]推荐的方法，以上面选出的产业的16个投入项和6个产出项分别作为两“类”，计算类内和类间的平均距离，得到的结果是投入项和产出项的类内平均距离分别为4.51和3.83，而两类间的平均距离则为7.24.由此可见，从产业系统地内部结构来看，投入项与产出项是明显分开的，各自成类的，因此要分别进行研究和应用.

2 数据集的降维与约简

按照我们选取的产业的投入项与产出项的数目，得出所采集到的投入项的数据集是16维的，其矩阵形式为31行×16列；类似地，产出项的数据集是6维的，其矩阵形式为31行×6列.可见，一个产业的主要经济指标的数据集的维数是比较高的.

显然，随着数据集维数的不断提高，数据将提供有关客观现象更加丰富、细致的信息，但同时又会给随后的数据处理工作带来前所未有的困难.这是因为常用的多元统计分析等方法只在数据集的维数不太高时才能有效地工作.当维数较高时，就必须采取一定的措施才能使处理和计算正常地进行，这类措施就是人们现在越来越多提及的数据集降维方法.

一般地，我们可以认为，无论何时，数据集的“本征维数”(或称作“固有维数”)总是比其“表象维数”小的多.通常的降维处理就是将原始数据集约简成只具有本征维数的新数据集，然后再进行处理.降维处理不仅可获得计算上的优势，还可大大改善数据的可理解性.实际的降维处理中，可采用线性方法，如主成分分析(PCA，Principal Component Analysis)具有简单性、易解释性、可延展性等优点.现今，如何将高维数据表示在低维空间中，并由此发现其内在结构是有关高维信息处理的研究中关键的问题之一[6].

依照高维数据集的降维理论，我们可以推知：并不一定需要将产业的主要经济指标的数据集中的所有变量均作为要素加以收入.实际上，这些数据常被一定数目的基本参数所控制.为说明观察到的数据的基本性质所需要的参数的最小数目被称之为数据集的“固有维数”，也就是所谓的“本征维数”，这些基本参数可能是单一的测量指标，也可能是它们的线性或非线性组合.

在实际问题中，有效的特征主要都是通过研究者的直觉而找到的.固有维数在本质上是数据集在空间中分布的局部特征.因此，如用聚类分析先进行初步的聚类和分类， 适当选取某些类中有代表性的样品点作为中心，并在它的周围建立一些小区域，则较容易估计其固有维数.而估计局部区域固有维数最直接的方法是在该区域中计算样本的协方差或相关系数矩阵的诸特征值，然后设定一个阈值，把大于此阈值的特征值的数目作为其固有维数.阈值的选择会影响到对维数的估计，其大小可根据情况取最大特征值的10%，5%或1%.

如果我们根据对数据集固有维数的估计能找到真正有代表性的特征的话， 那么对于减少所需测量指标的数目以及快速、深入地研究系统内部之间的关联等都是很有好处的.我们可以依据数据集的固有维数选定此数目的主要经济指标或其组合作为产业系统的要素，并以其数值作为产业发展之表征.

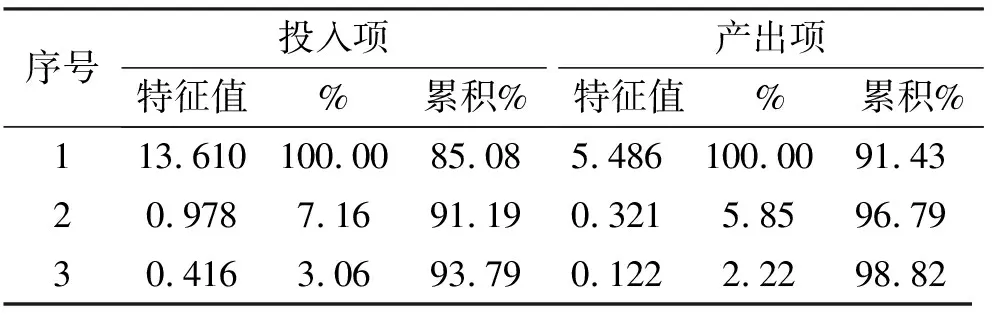
表2 投入项和产出项数据集矩阵的前3个特征值

我们对所采集到的投入项和产出项的数据集分别采用PCA方法进行了处理[7].投入项和产出项数据集矩阵的前3个特征值列于表2，而投入项和产出项各自的前2个因子的载荷则分别列于表3和表4.要指出的是，这些载荷都是因子经过方差最大正交旋转后的载荷，因此较大的载荷向少数几个变量上转移和集中，从而可以获得更明晰的解释.

表3 投入项数据集的因子载荷

由表2可以看到：对于投入项而言，第三特征值的数值已不到最大特征值的5%，第一(最大的)特征值的累积方差贡献就达85.08%，即已超过了阈值85%，前二个特征值的累积方差贡献更是超过了90%.因此可以推知，投入项数据集的固有维数最多只有1～2维，也就是说，可能只需一、二个指标或其组合就可以把投入项数据集的变化解释清楚.我们还检查过这16个投入项之间的相关系数，其数值都很高，绝大部分都在0.90以上.因此，可以说它们是“共线性”的，只需根据研究工作的实际需要任意地选定其中的一、二个指标作为系统的要素，应该都是可行的.如果我们再来看表3因子载荷表，根据其固有维数为1～2维，可以选因子Ⅰ作为系统的要素.在因子Ⅰ的变量组合中，依照载荷从大到小的排序，可以推知重要的及对于因子Ⅰ所起作用之强度较大的前5项是：1.技术改造经费支出(XA03，因子载荷 0.905)，2.(科技活动经费外部支出) 对研究院所和高校支出(XA10，因子载荷 0.877)，3.新产品开发项目数(XA07，因子载荷 0.845)，4.R & D 项目数(XA14，因子载荷 0.821)，5.企业单位数(XA02，因子载荷 0.792).

同样地，由表2还可以看到：对于产出项而言，第三特征值的数值也已不到最大特征值的5%，且第一(最大的)特征值的累积方差贡献就高达91.43%.因此可以推知：产出项数据集的固有维数也只有1～2维.若再参看表4，可以判定产出项数据集的因子Ⅰ应该是可以作为系统要素的一个变量组合，其中重要的，且作用强度较大的前3名指标是：1.新产品产值(XA26，因子载荷 0.847)，2.主营业务收入(XA23，因子载荷 0.684)，3.全部工业总产值(XA21，因子载荷 0.674).

通过以上分析和讨论可见，利用高维数据集降维理论及多元统计分析技术确实可以使产业系统大为简化，使我们有可能只用很少数的几个指标就可以完整地表征该系统的特征.而且，也使我们有可能去进一步地探究该系统的内部结构.

3 关联研究的方法

产业发展之表征与科技人才群体结构特征之间的关联，从数学上讲也主要是一种相关关系.对于变量(组)之间的相关关系，过去多采用相关分析或方差分析等方法进行研究.但由于一个完整的多元回归分析中包含了相关分析、方差分析和回归分析等几方面的内容，因此研究人员越来越愿意使用多元回归分析及其衍生方法进行计算与分析.在考察这种特定的关联时，对于单(因变量)对多(自变量)的关联，可借用多元回归分析等方法进行计算，而对于多(变量)对多(变量)的两组变量间的关联，则可以采用典型相关分析方法进行计算.

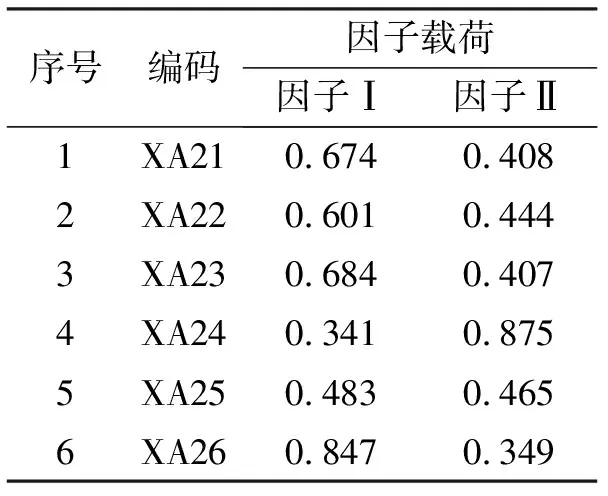
表4 产出项数据集的因子载荷

在上面的工作中，我们已经确认在产业系统中，不论是投入项还是产出项，它们的数据集的固有维数都只有1～2维，因而数据结构可以被大大地简化.一般地，只要选1～2个指标就已经有了充分的代表性.这就使我们有可能借用多元回归分析方法，将产业系统中的投入项或产出项中的某一项假设作“因变量”，而把几个群体结构特征设为“自变量”来考察因变量与自变量群之间的相关关系.我们知道：相关紧密程度的度量，并不会因为被设作因变量或自变量而改变，更不因此而改变变量间固有的、内在的因果关系.所以，如果仅仅是为了考察其相关关系的话，那么回归分析方法应当是可以借用的.由这些相关分析的结果，使我们有可能去进一步地探究该系统内部的关联状况，即系统的结构.有关系统结构的研究将另文专述. 总之，要想研究产业发展与科技人才群体结构之间的关联，首先要搞清每个系统中包含有哪些起决定性作用的要素，分别提取系统的特征或表征，确定系统内部和它们之间的关联的途径，即确定系统的结构，然后对表明这些关联的“链条”上的作用强度进行量化和计算，并作出人文社会科学意义下的诠释.只有全部完成了上述任务，才能说是对关联做了完整的、充分的分析与研究.

4 结束语

本工作以系统论的观点，从情报学领域的引文分析入手，利用作者同被引分析(ACA)技术，将产业和科技人才群体作为两个系统一起放入社会-经济大系统中来考察它们之间的关联.本文介绍了产业发展指标的选取，并应用数理统计方法，更多地参照实际情况，对表征产业系统发展数据集进行了降维处理，找出其固有维数.因为该固有维数较低或很低，从而可大大简化产业系统的结构，仅用少数或极少数指标即可表征系统的特性，从而使后面的关联研究变得十分简单.只需调用一些比较简单的多元统计分析方法，如多元回归分析等就可定量地研究产业发展与科技人才群体结构特征之间关联的作用强度.还可以使研究者有可能进一步构建起社会-经济大系统的因果关系模型，并且更容易给出在人文社会科学意义下的诠释.这一技术路线的成功实现，对于关联研究是至关重要的.

参考文献

[1] 耿海英，肖仙桃．国外共引分析研究进展及发展趋势[J]．情报杂志，2006，(12)：68-69，72.

[2] 马费成，宋恩梅．我国情报学研究分析：以ACA为方法[J]．情报学报，2006，25(3)：259-268.

[3] 方小容，艾学涛，蒋林宙，等．陕西皮革科技人才群体两个十年的同被引分析与比较[J]．陕西科技大学学报，2010，28(3)：175-180.

[4] 方小容．利用作者同被引分析技术对科技人才群体结构特征提取方法的研究[J]．现代图书情报技术，2010，(s)：58-62.

[5] 方小容，高档妮．基于同被引技术的科技人才群体结构特征的比较研究[J]．情报杂志，2010，29(9)：21-24.

[6] 谭 璐．高维数据的降维理论及应用[D]．长沙：国防科学技术大学博士学位论文，2005.

[7] 郭志刚．社会统计分析方法——SPSS软件应用[M]．北京：中国人民大学出版社，1999：87-115.