具有时滞的捕食-被捕食模型的稳定性及Hopf分支
刘晓娜, 陈斯养
(陕西师范大学数学与信息科学学院, 陕西 西安 710062)
0 引 言
1973年May研究了以下模型[1]
的稳定性和Hopf分支问题. 文献[2]研究了一类Logistic模型
的正平衡态局部稳定性和Hopf分支方向及周期解稳定性问题.
考虑到环境对食饵种群增长的影响,本文研究了以下模型
(1)
的局部稳定性及Hopf分支问题, 其中H(t)和p(t)分别表示食饵种群和捕食者种群在t时刻的密度, 参数r,K,α,β,b,c为正常数,τ表示捕食者从幼年到成年的成熟期(捕食者只有成年后才具有捕食能力)和被捕食者从幼年到成为食饵的生长期. 食饵的增长受时滞密度制约和其他因素的持续影响,取弱核函数F(t)=me-mt. 模型(1)满足初值条件
H(s)=φ1(s)≥0,p(s)=φ2(s)≥0,s∈[-τ,0],φi(0)>0,φi(t)∈C([-τ,0,R+),i=1,2
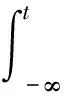
(2)
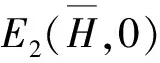
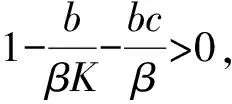
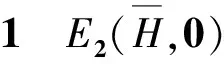
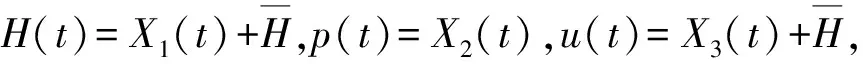
(3)
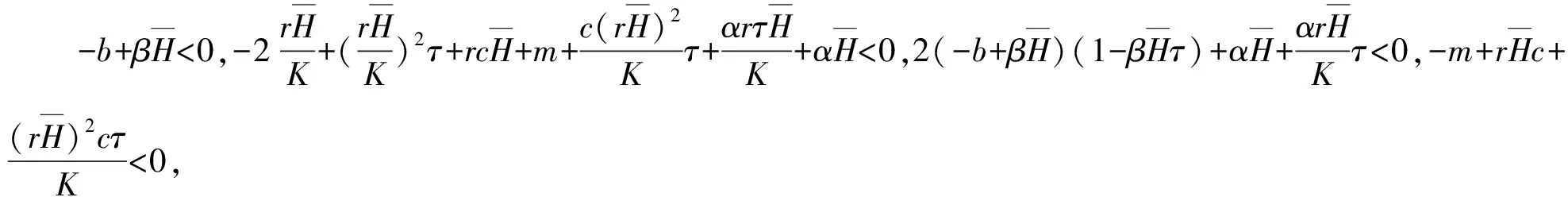
证明 选取Lyapunov泛函
则V(t;X1,X2,X3)沿着系统(3)的全导数为
由Lyapunov稳定性理论可知定理1得证.
2 正平衡态的稳定性与Hopf分支存在的条件
作变换H(t)=X1(t)+H*,p(t)=X2(t)+p*,u(t)=X3(t)+u*得到式(2)在E*处的线性系统
(4)
系统(4)特征方程如下
λ3+a1λ2+a2λ+a2λ2e-λτ+a4λe-λτ+a5λe-2λτ+a6e-λτ+a7e-2λτ+a8=0
(5)
其中a1=b-αp*+m,a2=rcH*m-αbp*+mb-αmp*,a3=-b+r(1-cH*),
a4=2αbp*+br(1-cH*)-bm+mr(1-cH*),a5=-br(1-cH*),
a6=2αbmp*+brm-2rbcmH*,a7=-brm(1-cH*),a8=rbcmH*-αbmp*.
引理2 当τ=0时,式(5)的所有根均具有负实部.
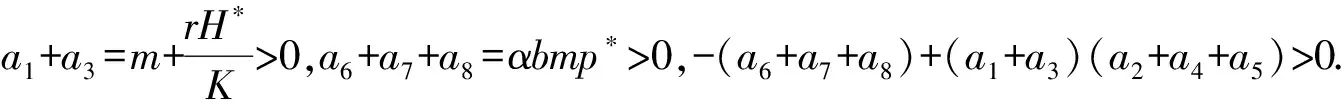
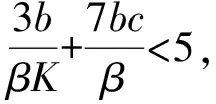
证明 假设式(5)存在一对纯虚根±iω(ω>0),把λ=iω代入式(5), 分离实虚部得:
(6)
经计算可知
(7)
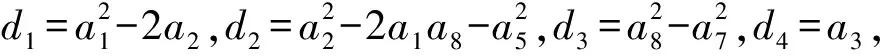
d5=a1a4-a2a3-a3a5-a6,d6=-a4a7-a4a8+a2a6+a5a6,
d7=a4-a1a3,d8=a3a8+a4a5+a1a6-a3a7-a2a4,d9=a6a7-a6a8.
因为sin2ωτ+cos2ωτ=1,由式(7)可得
ω12+f1ω10+f2ω8+f3ω6+f4ω4+f5ω2+f6=0
(8)
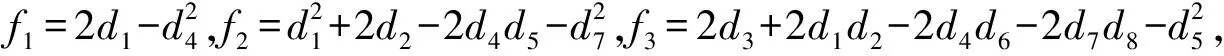
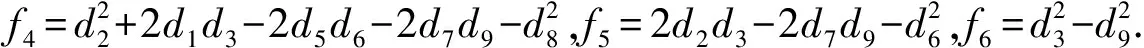
令z=ω2, 则式(8)化简为
z6+f1z5+f2z4+f3z3+f4z2+f5z+f6=0
(9)
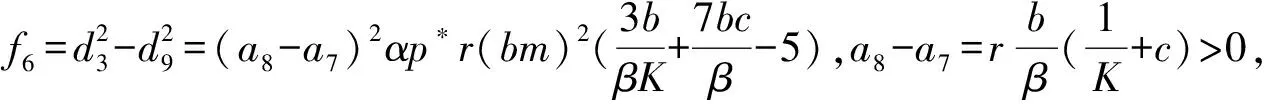
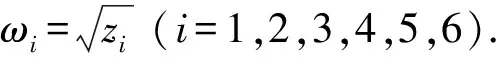
从而
其中
由以上分析可得如下定理2.
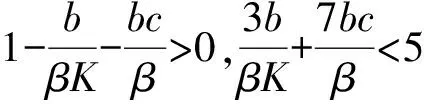
3 Hopf分支的方向与周期解的稳定性
在这一部分,将采用规范型方法及中心流形定理分析系统(2)在临界值τ0处的Hopf分支方向及周期解的稳定性.
引理5[4]μ2决定了Hopf分支的方向,如果μ2>0(0),则Hopf分支是超临界(亚临界)的, 在τ>τ0(<τ0)时,分支周期解存在.β2决定了分支周期解的稳定性,β2<0(>0)分支周期解是稳定的(不稳定的).T2决定了分支周期解的周期,如果T2>0(<0)周期是增加(减少)的.
4 数值模拟
例1
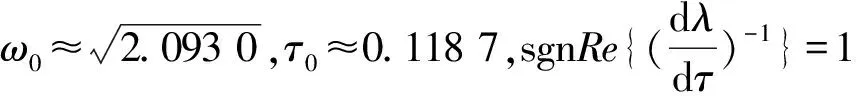
从图1(a)~(f)中可以看出τ<τ0时出现Hopf分支, 周期解是不稳定的, 振幅减小(见图1(a)~(b)), 周期比τ=τ0时增大(见图1(c)~(d)),与引理5结论相符.τ<τ0时振幅减小,最终趋于稳定(见图1(e)). 当τ大于τ0系统(2)的正平衡点E*是不稳定的, 种群可能趋于灭绝(见图1(f)).
例2
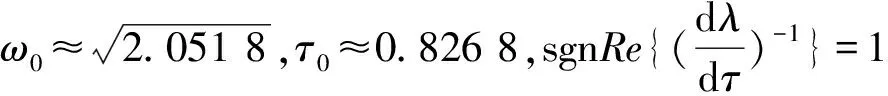
从图2(a)~(f)可以看出τ>τ0时出现Hopf分支, 周期解是稳定的(见图2(a)~(b)),周期比τ=τ0时减小, 与引理5结论相符(见图2(c)~(d)).τ<τ0时(微小邻域), 系统(2)的正平衡点E*是渐近稳定的(见图2(e)~(f)),与定理1结论相符.
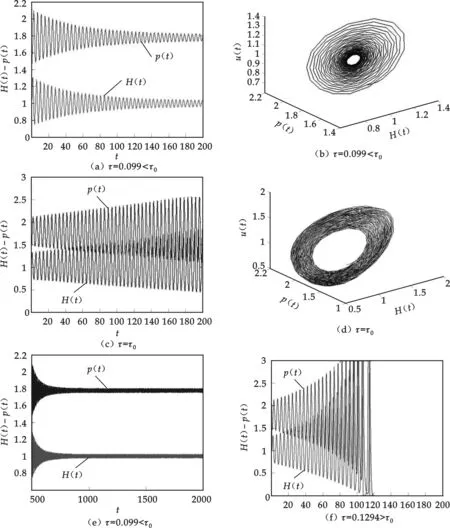
图1 τ取不同值时周期解扰动情况
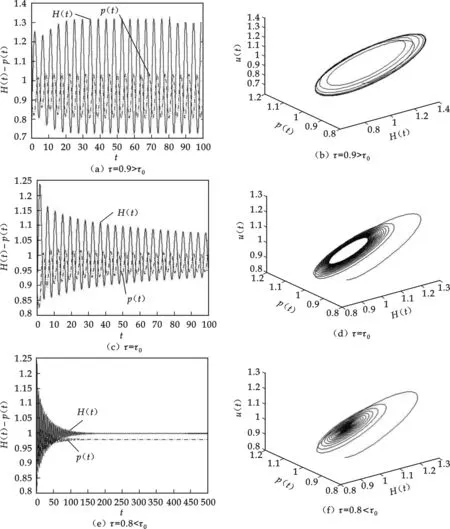
图2 τ对稳定性的影响
例3 对模型中不同参数取值进行对比分析,其中c,m对系统(1)的影响见表1;α,β,b,c,r,K对系统(1)的影响见表2.
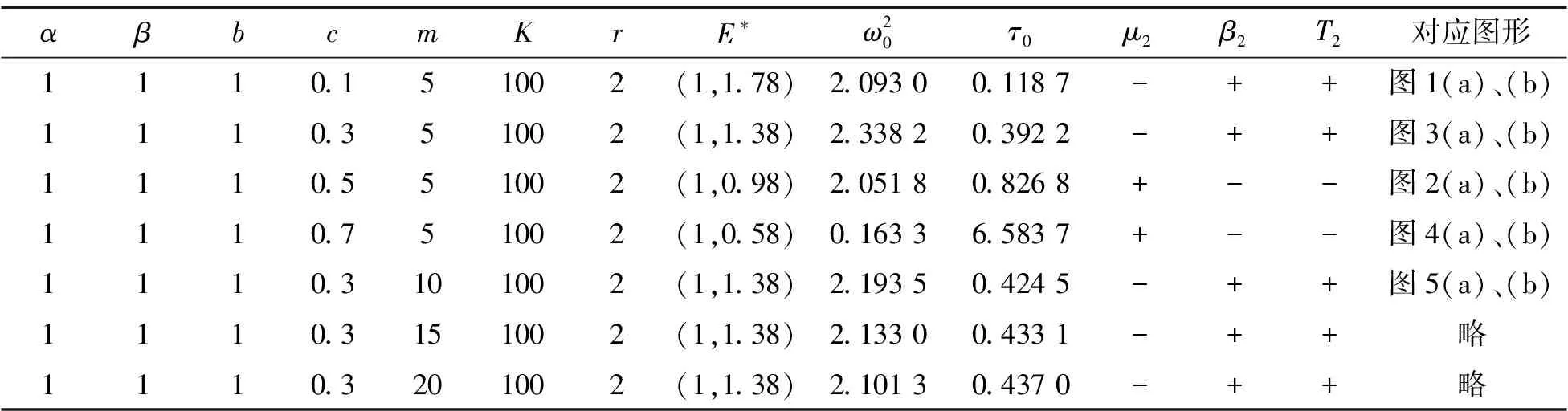
表1 系数c,m对系统(1)的影响
从表1可以看出环境对食饵增长率的影响可以扩散至整个系统:
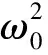
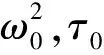
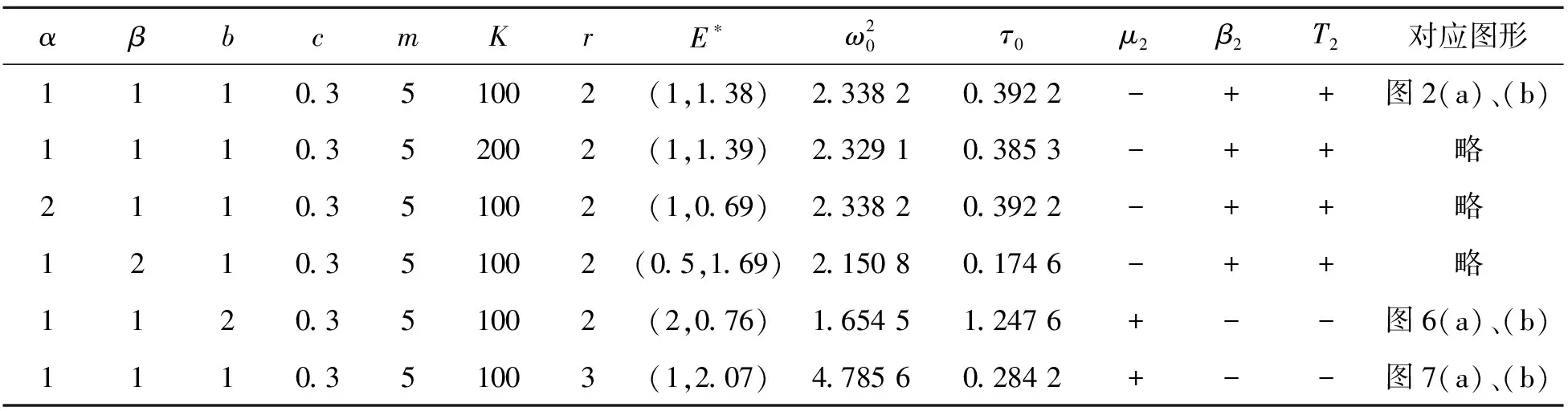
表2 其它参数对系统(1)的影响
从表2中可以看出:
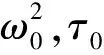
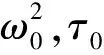
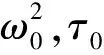
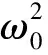
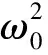
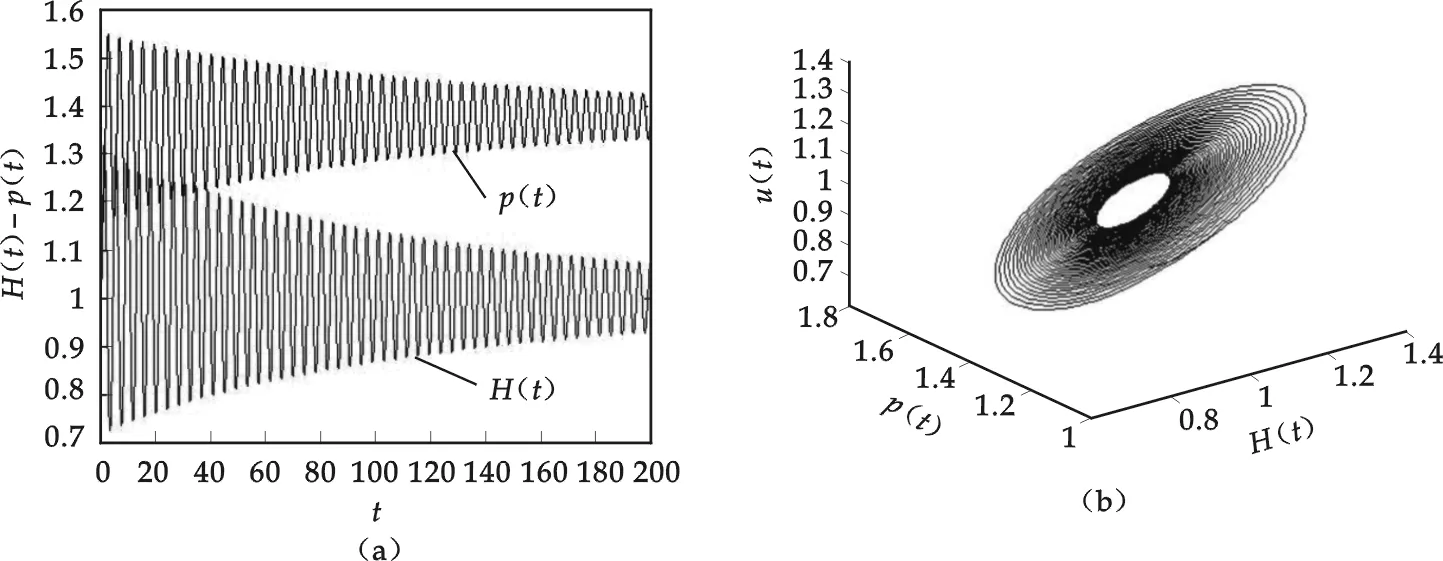
图3 τ=0.389<τ0产生Hopf分支
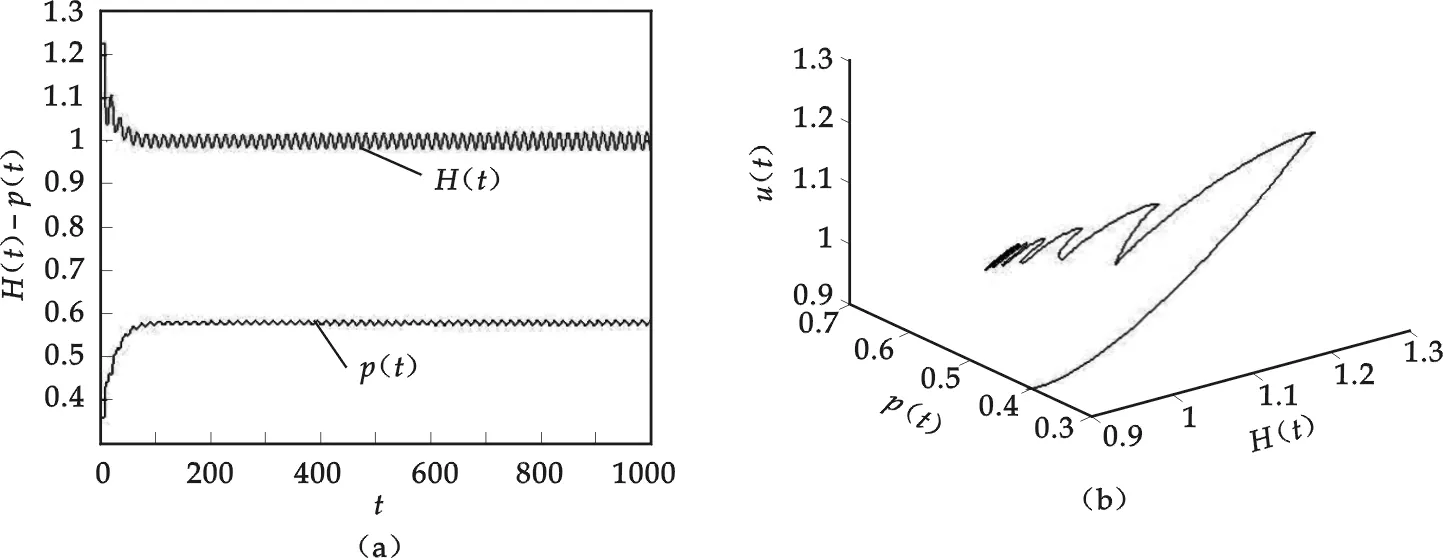
图4 τ=6.783 7>τ0产生Hopf分支
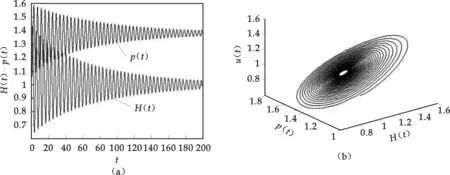
图5 τ=0.418<τ0产生Hopf分支
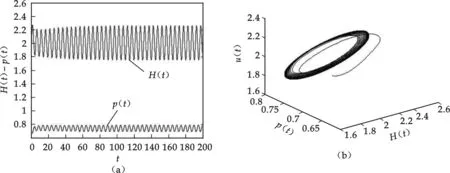
图6 τ=1.3>τ0产生Hopf分支
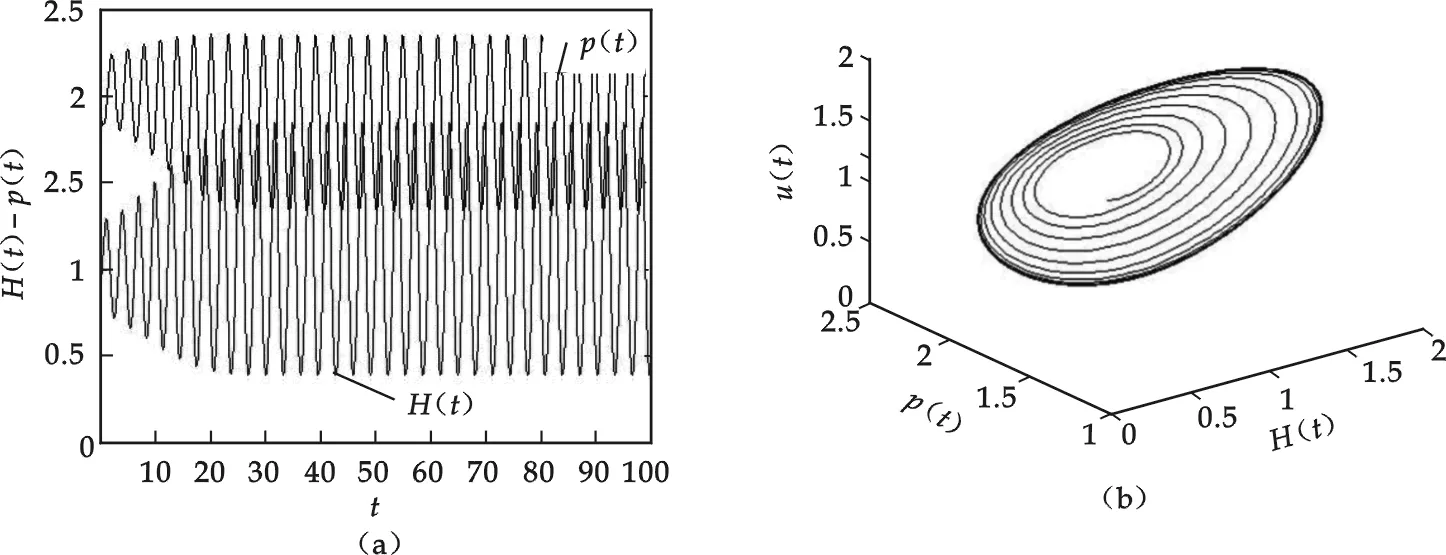
图7 τ=0.3>τ0产生Hopf分支
参考文献
[1] R.M.May. Stability and Complexity in Model Ecosystems[M].Princeton Univ.Press,New Jersey,U.S.A,1973.
[2] Y.song. Y.peng. Stability and bifurcation analysis on logistic nodel with discrete and distribute delays[J]. Appl.Math.Comput.,2006,(181): 1 745-1 757.
[3] B.Hassard, D.Kazarinoff,Y.wan. Theory and Applications of Hopf Bifurcation[M].Cambridge University Press,Canbridge,1981.
[4] Aying Wan, Junjie Wei. Hopf bifurcation analysis of a food-limited population model with delay[J]. J.Math.Anal.Appl.,2010,(11):1 087-1 095.
[5] R.M.May.Time delay versus stability in population models with two and three trophic levels[J]. Ecology,1973,(4):315-325.
[6] 陈兰荪, 宋新宇, 陆征一.数学生态学模型与研究方法[M].成都:四川科学技术出版社,2003.
[7] 薛定宇, 陈阳泉.高等应用数学问题的Matlab求解(第二版)[M].北京:清华大学出版社,2009.
[8] 杨颖茶,陈斯养.一类二阶非自治时滞方程的线性振动问题[J].陕西科技大学学报,2006,24(5):119-123.

