HEMP 场激励下交直流高压输电线 耦合响应概率分布
卢斌先 郝晓飞 罗艳华 王泽忠
(华北电力大学高电压与电磁兼容北京市重点实验室 北京 102206)
1 引言
随着电气电子设备和电磁环境的复杂化,影响电磁兼容分析的随机变量增多。因此概率和统计的方法在电磁兼容研究领域得到了应用[1-2]。高空核爆电磁脉冲(HEMP)、闪电电磁脉冲(LEMP)和GIS变电站开关操作产生空间电磁场对电力系统和通信系统的线缆产生干扰。外场激励下传输线耦合响应问题的研究是电磁兼容领域的重要课题。由于传输线分析法简单、易于考虑参数的频变特性,因此基于传输线理论提出了多种外场激励下的耦合响应分析方法[3-5]。文献[6-11]利用传输线理论研究了相对于传输线空间电磁场入射参数固定的情况下,空间电磁场激励下线缆终端的电流和电压响应。但在实际应用中,对于具体的传输线来说,传输线的结构参数是确定的,而空间的电磁场参数具有一定的随机性。文献[12-13]在电小传输线和单一随机变量的假设前提下,在频域内对均匀平面波激励下无损二导体传输线终端电流响应的概率密度进行了分析,对于复杂的场线耦合问题无法应用。基于外场激励下多导体节点导纳方程[14],在假设激励场为均匀平面波的前提下,应用蒙特卡洛方法分析了同时含有三个随机变量的多导体传输线电压时域耦合响应绝对值峰值概率分布规律。在很多实际应用中,空间电磁场经常是从某一个范围入射,而不是从各个方向入射。因此只考虑入射参数范围在[0,π/2]的情况。
2 外场激励下传输线频域终端响应
空间场与传输线相对位置如图1 所示。图中①、②和③分别为各导体的标号。ψ 为电磁波相对于传输线的入射仰角,ϕ 为电磁波相对于传输线的入射方位角,α 为入射电磁场的极化角。传输线与x 方向平行。基于外场激励下Taylor 多导体传输线模型,经过简单的数学处理可得外场激励下耦合多导体传输线终端响应的节点导纳方程[14]为

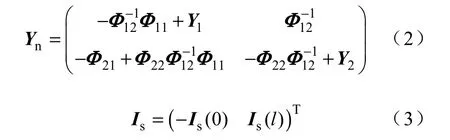

图1 传输线与入射波相对位置 Fig.1 Relative position of transmission line and incident plane wave

该矩阵为多导体传输线输入输出端口的传输矩阵,Φ11和Φ22为无量纲的量,Φ12和Φ21的单位分别为Ω和S。Y1和Y2为终端节点导纳矩阵。Is为传输线沿 线分布电源在传输线首端和末端的等效电流源。

式中

式中,ω为角频率;μ0为自由空间的磁导率;hi为第i 根导体距地面的z 方向的高度;C 为多导体传 输线的单位长度电容矩阵。和为考 虑大地影响、没有导体存在时图1 所示坐标系各方向的电场与磁场分量,上标ex 表示激励场。
应用式(1)可以在频域分析空间电磁场在多导体传输线终端产生的耦合电压响应,傅里叶分析上限频率为500MHz。再根据入射电磁波的频谱,利用IFFT(快速傅里叶反变换)即可求出传输线时域耦合响应。取时域响应绝对值的峰值后即可以进行概率分析。
3 基于蒙特卡罗方法耦合响应的概率分布研究
通常空间入射电磁波随机的入射角ψ、极化角α 和方位角ϕ 满足均匀分布。模拟随机变量的基础是随机序列的产生,产生随机序列的方法有多种。本文采用的方法是乘同余法,它采用迭代运算得到一个在[0,1]区间的均匀分布的数列{ξ1,ξ2,…,ξn},其迭代公式为

其中,M=2S,S=32,m=513。x0最好随机取一个4q+1 型的数(q 为任意整数);m 取52k+1型的正整数;这里的k 对应的2k+1 是使52k+1为计算机所能容纳的最大奇数。对于[a,b]中的均匀分布的随机变量

在产生空间随机入射的电磁波的入射角ψ、极化角α和方位角ϕ 三个随机变量时,q 分别取1,2,3,随机变量取值范围为[a,b]=[0,π/2]。通过上述方法产生210组随机变量[ψi,αi,ϕi]。
4 仿真研究
4.1 高压交流输电线终端响应绝对值峰值分布概率
仿真过程中设均匀电磁波作用于传输线上,电场强度为
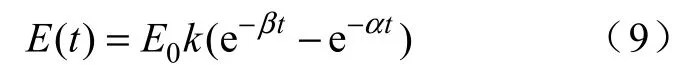
Bell 和IEC61000 标准HEMP 参数的对比见下表。由于高压架空传输线距离较长,瞬态电磁场持续时间较短,因此仿真过程中采取下列三种假设对耦合响应进行分析:
(1)假设电磁脉冲照射到高压长传输线远离变电站处,传输线两端接特性阻抗,这里所述的特性阻抗是指忽略导体之间的相互影响时,单导体和大地之间传输线特性阻抗。
(2)假设电磁脉冲照射到变电站的入口处附近,此时由于距离变电站较近,因此必须考虑变电站的影响。此时假设从变电站入口看进去,变电站可看作无限大系统,即传输线变电站一端短路,另一端接特性阻抗。
(3)考虑电磁波照射到传输线变电站入口处的输电线上,变电站主开关断开,即传输线变电站一端开路,另一端接特性阻抗。

表 两种HEMP 标准参数对比 Tab. Comparison of parameters between two standard fields
仿真研究的三相输电线结构如图2 所示,线长100m。S1 和S2 为两屏蔽地线,φ14.84cm;C1、C2和C3 为三相导体,φ 23.7cm,各导体之间的尺寸如图2 所示。图3 为输电线首端接特性阻抗,末端短路响应概率分布曲线,图4 为输电线首端为特性阻抗,末端为开路各结点电压的概率分布曲线,图5为输电线两端接特性阻抗各节点电压的概率分布曲线。图中V 表示电压,i 表示电流,1、2 和3 分别为首端节点标号,4、5 和6 为末端节点标号。
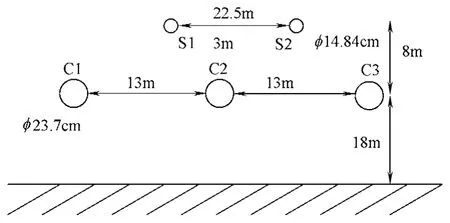
图2 考虑屏蔽线的三相输电线路布置图 Fig.2 Layout of HVAC concluding shielding lines

图3 输电线首端接特性阻抗,末端短路 响应概率分布曲线 Fig.3 Probability distribution when terminated with characteristic impedance at sending ends,shorted at receiving ends

图4 输电线首端为特性阻抗末端开路的概率分布曲线 Fig.4 Probability distribution when terminated with characteristic impedance at sending ends,opened at receiving ends
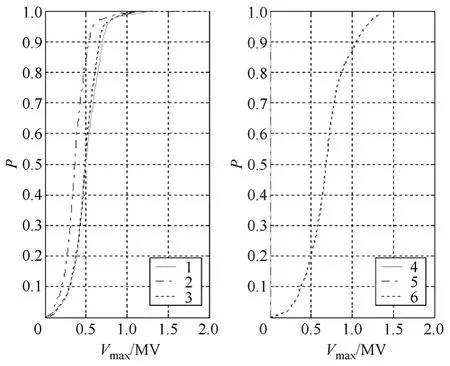
图5 输电线两端接特性阻抗概率分布曲线 Fig.5 Probability distribution when terminated with characteristic impedance
对比图3~图5 可以看出随着终端阻抗的变化终端响应峰值的概率分布曲线发生了变化。尽管图4 和图5 概率分布曲线波形相似,但峰值不同。
4.2 高压直流输电线终端耦合响应峰值的分布概率
高压直流输电线布置图如图6 所示,假设线长为100m。图7 为输电线两端接特性阻抗各节点电压的概率分布曲线。从图中可以看出首末端电压的概率分布曲线基本相同。
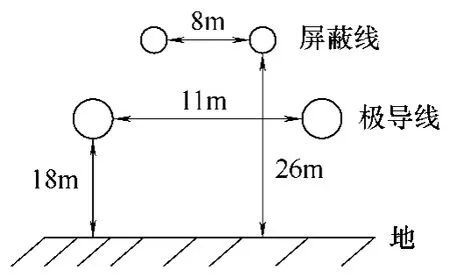
图6 考虑屏蔽线的高压直流输电线路布置图 Fig.6 Layout of HVDC concluding shielding lines

图7 输电线两端接特性阻抗概率分布曲线 Fig.7 Probability distribution when terminated with characteristic impedances
4.3 不同波形HEMP 激励下终端耦合响应峰值的分布概率比较
IEC61000−2−9 民用标准越来越广泛地被引用[15]。输电线首端为特性阻抗末端短路IEC61000−2−9场激励下仿真波形图如8 所示,IEC61000−2−9 相应参数见4.1 节。
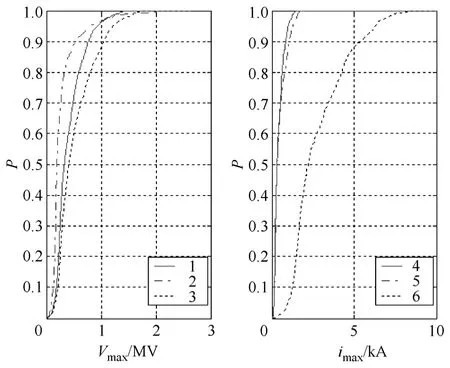
图8 输电线首端为特性阻抗末端 短路概率分布曲线 Fig.8 Probability distribution when terminated with characteristic impedance at sending ends,shorted at receiving ends
5 结论
(1)随着终端端接条件的改变,终端响应的概率分布曲线变化较大。
(2)通过研究发现在同样的传输线端接条件下,在累积概率为0.9 时,不论是交流输电线还是直流输电线,不论是首端还是终端响应,Bell 标准HEMP 场作用产生耦合响应的峰值高于IEC61000−2−9标准HEMP 场作用产生耦合响应。
(3)对于三相交流输电线电磁波入射端来说,不管是IEC61000−2−9 标准还是Bell 标准,在相同累积概率情况下,中间相的耦合响应峰值总是小于两边相的耦合响应峰值。
(4)对于直流输电线在两端都接特性阻抗时,首端和终端响应概率分布曲线基本相同。
尽管该仿真研究需花费近20min 的时间,但是仿真结果对了解强电磁脉冲作用下,架空线终端耦合响应峰值分布规律具有很好的帮助作用,为HEMP 场激励的防护策略研究提供了依据,为分析和预测架空线路在HEMP 场作用下绝缘损坏概率提供了分析的思路。
[1] 胡皓全,赵家升.用蒙特卡洛方法对随机电磁干扰进行预测分析[J].电波科学学报,2001,16(2):280- 282.
Hu Haoquan,Zhao Jiasheng.Monte Carlo method of predicting random electromagnetic interference[J].Chinese Journal of Radio Science,2001,16(2):280- 282.
[2] H St John R,Holland R.Field-component statistics of externally illuminated overmoded cavities[J].IEEE Trans.on EMC,2000,42(1):125-134.
[3] Taylor C D,Satterwhite R S,Harrison C W.The response of a terminated two-wire transmission line excited by a nonuniform electromagnetic field[J].IEEE Trans.on Antennas Propagation,1965,AP-13:87-89.
[4] Agrawal A K,Price H J,Gurbaxani S H.Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field[J].IEEE Trans.on EMC,1980,EMC-22:119-129.
[5] Racchidi F.Formulation of field to coupling equations transmission line in terms of magnetic excitation field[J].IEEE Trans.on EMC,1994,35(3):404-407.
[6] 谢彦召,孙蓓云,聂鑫,等.有界波电磁脉冲模拟器下短线缆效应的理论和实验研究[J].强激光与粒子束,2005,17(11):1717-1720.
Xie Yanzhao,Sun Beiyun,Nie Xin,et al.Response of a short single-wire line illuminated by an EMP simulator[J].High Power Laser and Particle Beams,2005,17(11):1717-1720.
[7] 谢彦召,王赞基,王群书.电磁脉冲模拟器下架空线缆响应的实验研究[J].中国电机工程学报,2006,26(24):200-204.
Xie Yanzhao,Wang Zanji,Wang Qunshu.Experi- mental study on the response of aerial wires illuminated by simulated electromagnetic pulse[J].Proceedings of the CSEE,26(24):200-204.
[8] 谢彦召,王赞基,王群书.架空多导体传输线缆的电磁脉冲响应计算[J].清华大学学报(自然科学版),2006,46(4):449-452.
XieYanzhao,Wang Zanji,Wang Qunshu.Calculation of HEMP coupling to aerial multi-conductor transmission lines[J].Journal of Tsinghua Univ (Sci & Tech),2006,46(4):449-452.
[9] 卢斌先,王泽忠,程养春.基于拉氏反变换的传输线耦合电流半解析解[J].电网技术,2007,14(14):11-25.
Lu Binxian,Wang Zezhong,Cheng Yangchun.Laplace inverse transformation based semi-analytical solution of coupling currents of transmission line illuminated by electromagnetic pulse[J].Power Technology,2007,14 (14):11-25.
[10] Gurpreet S Shinh,Natalie M Nakhla,Ram Achar,et al.Fast transient analysis of incident field coupling to multiconductor transmission lines[J].IEEE Trans.on EMC,2006,48(1):57-73.
[11] Marcello D’Amore,Maria Sabrina Sarto,Alberto Scarlatti.Modeling of magnetic-field coupling with cable bundle harnesses[J].IEEE Trans.on EMC,2003,45(3):520-530.
[12] Diego Bellan,Sergio Pignari.A probabilistic model for response of an electrically short two-conductor transmission line driven by a random plane wave field[J].IEEE Trans.on EMC,2001,43(2):130-139.[13] Ianoz M,Nicoara B I C,Radasky W A.Modeling of an EMP conducted environment[J].IEEE Trans.on EMC,1996,38(3):400-413.
[14] 卢斌先,王泽忠.基于Agrawal 模型和Taylor 的耦合多导体传输线耦合电压结点导纳法分析[J].电工技术学报,2007,22(10):145-149.
Lu Binxian,Wang Zezhong.Nodal admittance method for response of multiconductor transmission line excited by electromagnetic field[J].Transactions of China Electrotechnical Society,2007,22(10):145-149.
[15] Tesche F M.Topological concepts for EMP interaction[J].IEEE Trans.on EMC,1978,20(1):60-64.

