基于MATLAB的一种并联顶举机构逆解与工作空间分析

姚荣华，陈品志，何鹏飞

YAO Rong-hua，CHEN Pin-zhi，HE Peng-fei

（北京理工大学 机械与车辆学院，北京 100081）

0 引言

在震后救援工作中，传统的顶举机械如千斤顶只能在单一方向上进行顶举工作，一旦顶举方向需要变化则千斤顶必须卸载后重新安装顶举，如果方向还有偏差，则须再次卸载以变换顶举变向，这样反复调整浪费了大量时间，严重限制了震后施救效率的提高。针对以上问题，本课题组设计了一种空间三自由度的顶举救援机器，该顶举机械在重载下可以实时调整顶举姿态，改变项举方向，从而大大提高顶举工作的效率。

1 机构简介

机构简图和工作样机分别如图1、图2所示，该机构有三个空间自由度，靠三根双作用液压杆的伸缩控制整个机构的运动。空间并联顶举机构实现了空间状态实时变换的功能，机构底部可适应各种不同的工作环境方便安装。机构的上下平面的工作范围均可调整，上平台半径r调节范围200~290mm，下平台半径R为300~420mm，杆的长度为430~680mm，C1、C2、C3为底部平台的三个固定点，A1、A2、A3为上平台的三个球绞点，底部三个点与三根杆的连接使用销钉连接只能绕销钉的轴线方向进行旋转。机构上的三根杆C1A1、C2A2、C3A3是三根液压杆即该机构的三个自由度。

图1 机构简图

图2 工作样机

液压杆的行程是通过液压系统一系列的电磁阀控制的。单片机中输出的电信号通过调制解调，功率放大之后去控制电磁阀来调节液压油的流量，最终实现对机构的电、液、机控制。然而在控制中最困难的就是根据想要上平面姿态去求三根杆的行程，这就需要单片机能够根据实际所需姿态迅速反求出C1A1、C2A2、C3A3的长度，然后给出电信号进行控制。求三杆的长度要进行逆解分析，而控制中还要知道机构的运动空间，防止机构运动到空间的奇异点从而破坏机构。求机构的空间奇异点就要求出机构的空间运动包络面，反求出杆长的伸缩范围，这样机构的控制就在理论上实现了。以下介绍了针对该机构控制的理论基础和用MATLAB计算的方法。

2 机构逆解与工作空间分析

点C1、C2、C3在定坐标系O-XYZ下的绝对坐标，其中R1、R2、R3是机构底部三根连接杆的工作长度，z1、z2、z3为固定点的安装高度。

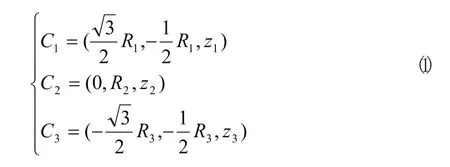
点A1、A2、A3在动坐标系P-X1Y1Z1下的相对坐标，其中r1、r2、r3为顶部三根杆的工作长度

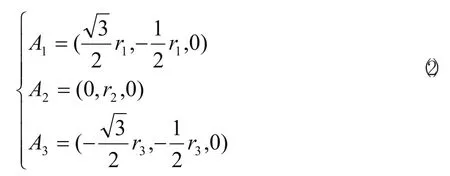
动坐标系P-X1Y1Z1对定坐标系O-XYZ的可用欧拉角表示的齐次坐标变换矩阵描述。用欧拉角描述机构空间姿态，由于欧拉角表示的旋转矩阵只有三个参数，所以用欧拉角将平台的位姿参数与变换矩阵联系起来，方便了求解运算。

设上平面的单位矢量为Nt=（ntx,nty,ntz）T，欧拉角为α、β 、γ，运动平台与绝对坐标系坐标轴的方向余弦角为θx、θy、θz。

为了计算方便以及保证 ntx、nty、ntz与 α、β、γ 为单值对应，需要对欧拉角做如下规定：

平台的法向单位矢量即为方向余弦：

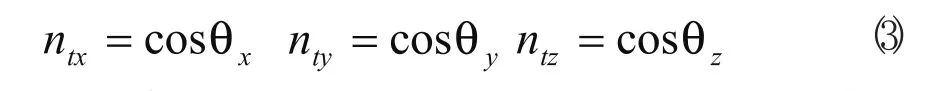
根据实际的运动情况，不能取负值，所以有

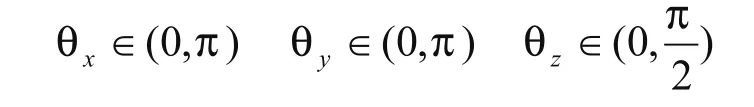
用欧拉角表示的平台姿态的旋转矩阵为：

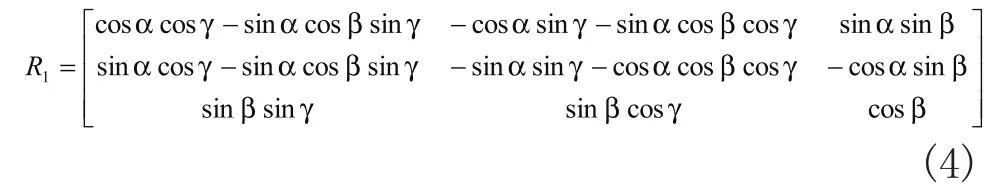
由于平台的轴线与所定义的动坐标系的Z1轴重合，所以旋转矩阵R1的最后一列正好是动坐标系轴的单位矢量，可以得到三个方程：

将平台的空间姿态角通过上式转化成为欧拉角的表示。

根据，两个欧拉角可以由平台的方向余弦角完全确定，欧拉角表示的动平台姿态的旋转矩阵的每一列分别表示动平台坐标系轴对轴的方向余弦，于是有：

其中对应的元素相等，还有加上平台不自转的条件-α=γ：。在结合实际模型，还应有约束条件：

其中u1、u2、u3为三个转动副的轴线的单位方向矢量，此外机构杆长也为约束条件。

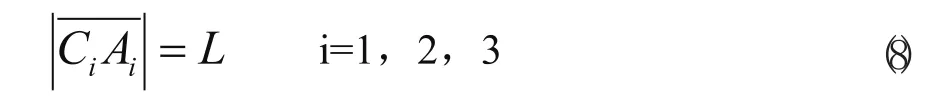
对于（7）式中的方程α、β 、γ为三个未知数，而θx、θy、θz为三个上平台空间运动的姿态角为已知量，并且有cos2θx，cos2θy，cos2θz=1所以方程组（5）中只有两个式子是独立的，而θx、θy、θz中也只有两个独立的变量，在加上上平台中心点的纵坐标，该机构的数学描述中只有三个独立的变量，即该机构只有空间的三个自由度。

对实际机构模拟还应加上顶部运动平台球角运动角度的约束条件，是通过运动杆的单位矢量与平台三定点与中心形成的向量的夹角确定，限定范围为30度。

3 基于MATLAB的逆解与工作空间仿真

在MATLAB中要先对机构进行描述，用MATLAB的程序语言描述运动平面内的三点在动坐标系中的位置和底部三点在定坐标系中的位置，然后利用动坐标系相对于定坐标系的坐标变换矩阵将描述机构的所有的点均转换到一个统一的坐标系中研究。

在计算机仿真中利用数值计算的方法非常利于简化程序而且运算简单。根据平台的最终空间要达到的空间姿态去反求其他各点的位置和杆的长度。这里通过循环语句对机构的各种空间姿态进行取值和密化，由于机构为空间三自由度，所以只要对其中的三个变量进行循环自动赋值就可以取到机构所能达到的空间姿态。

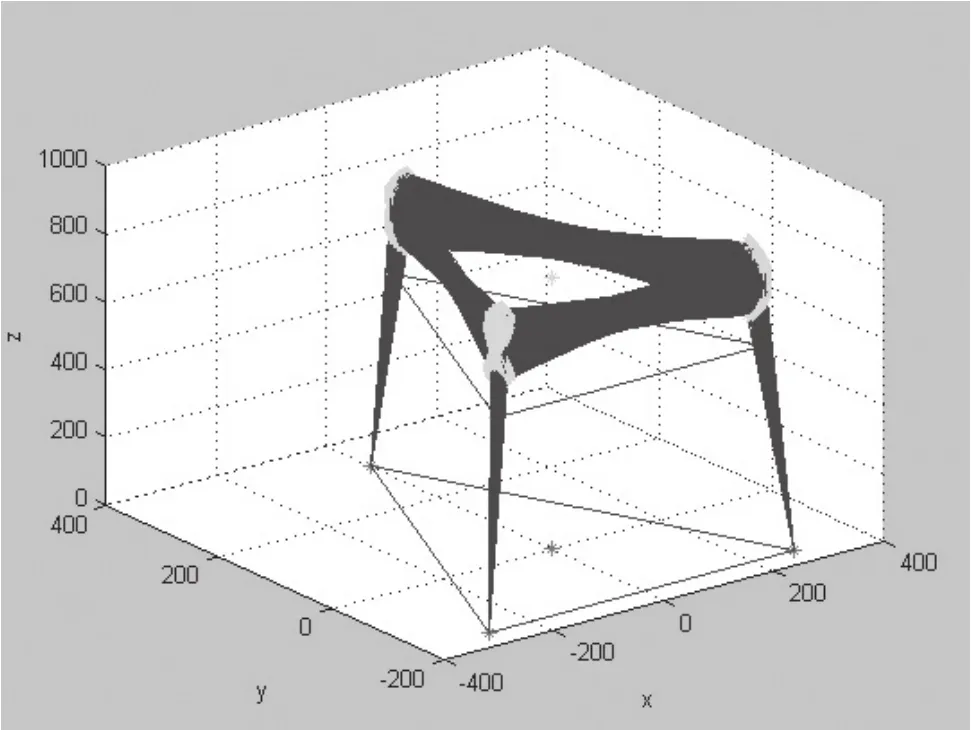
图3 机构的逆解分析

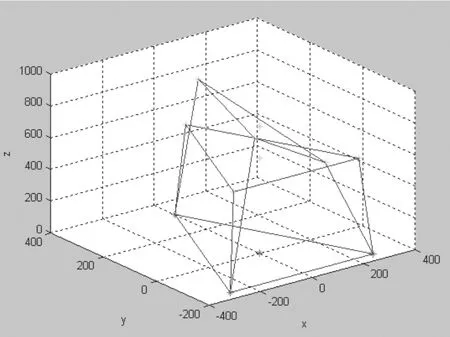
图4 机构的工作空间分析

进行空间机构仿真时，对于机构在实际运动中存在的约束是通过对空间中已求出的理想点进行再次分析模拟的。用理想模型中的出的机构空间点进行杆长和向量空间夹角的描述，通过如杆长和夹角再对这些理想点进行筛选，最终就可以得到机构的实际运动空间。

在程序中进行自动取值去掉而输入自定的欧拉角（根据平台姿态用公式得出），则可计算出该姿态下的平台动杆所应达到的杆长。对所取的空间姿态向量越密集，则对平台的空间姿态描述越精确。图3为在已知上平面的θx、θy、Z的条件计算出杆长绘制的图，由于没有加球绞限制和杆长限制，所以达到的空间旋转范围大，是对逆解分析算法的一种验证。图4是加上限制条件之后在空间某一固定高度绘制出的机构空间工作范围，可以看到机构在固定高度上的旋转空间范围是比较有限的，这主要是在设置球绞工作范围时的取值较小，在实际产品中使用的直线杆端球轴承的工作范围是30度，若要增大产品的工作范围就必须定做球绞角度更大的轴承。通过工作空间分析知道了机构的空间工作范围，提供了进行控制的杆长参数，确定了三杆联动在达到预期位置过程中杆长的变化范围与最终确定值。

4 对比分析

实际试验发现机构在某一运动高度时，其旋转空间的范围不是很大，三根杆长的伸缩范围受顶部球绞的旋转角度制约严重，从而造成三根杆的长度差并不是很大即上平台的空间旋转范围较小。但由于机构垂直方向上的运动不受球绞的制约且伸缩范围大，机构在整个空间的运动范围能够满足设计之初多方向顶举的要求，并且在实际试验时，由于机械零件的公差的存在使机构运动并不严格按照计算时的约束进行运动，运动范围稍大于计算得到的范围。

[1]韩建有.高等机构学[M].北京：机械工业出版社,2004．

[2]刘峰,陈文凯.3自由度并联机器人的研究现状和发展前景[J].企业技术开发,2006,（1）.