基于小波系数变换的小波阈值去噪算法改进

王宏强， 尚春阳， 高瑞鹏， 李子楠

（西安交通大学 机械工程学院，西安 710049）

信号的去噪一直是信号处理中备受关注的一个问题，而小波去噪是近年来兴起的极为有效的去噪方法之一［1］。其中小波阈值去噪由Donoho和Johnstone提出［2－5］并证明其逼近原信号的最优估计［1］，且在 Besov空间中，小波阈值去噪与线性去噪方法相比，收敛速度更快［1－3］。

近年来对于小波阈值去噪，学者们主要关注三个方面：阈值去噪函数的建立、阈值的确定及小波基的选择。在阈值去噪函数的建立方面，Donoho和Johnstone等人［6，7］于1995年提出了硬阈值方法和软阈值方法，之后有Garrote阈值函数及Gao和Bruce提出的半软阈值方法以对上述硬阈值和软阈值两种去噪方法进行了改进。在选取最优的去噪阈值方面，学者们提出了许多选取方法，如固定阈值（sqtwolog）、最小极大方差阈值（minimaxi）、基于Stein无偏似然估计阈值（rigrsure）及选择启发式阈值（heursure）等［8－10］。

小波阈值去噪基本原理是：正交小波变换具有很强的去数据相关性，它能够使信号的能量在小波域集中在一些大的有限的信号的小波变换系数要大于噪声的小波变换系数，也即可以认为幅值比较大的小波系数一般以信号为主，而幅值较小的系数在很大概率上是噪声。于是可以找到一个合适的阈值，小波系数大于阈值的认为其是由信号引起的，而小于阈值的小波系数则由噪声引起的，从而可以对由噪声引起的小波系数进行萎缩来去除噪声［8］。因此小波阈值去噪的一个难点在于区分噪声和信号。小波系数中原信号的一些细节与噪声较多的区域比较接近，容易被当作噪声信号滤掉。

本文对传统的小波阈值去噪方法进行了较为深入的研究并予以了改进，在小波阈值去噪的方法中加入了两个步骤：

（1）对信号小波分解后的各层小波系数进行变形，将中间易混淆区域的差别放大，两端不易混淆的值域缩小，以利于去噪时对噪声的识别；

（2）阈值去噪后，对去噪后的小波系数进行恢复处理，将前面变形后的小波系数予以恢复。

结果表明利用本文的方法可以将细节信号与噪声之间的差别加大，从而更好的复现原信号。

1 小波系数的变换

假定观测信号向量为y=［y0，y1，y2，…，yN－1］T，有如下式子：

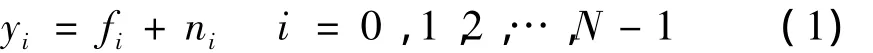
其中fi为函数f的抽样，nj是分布为N（0，σ）的高斯白噪声。去噪的目标是使所得的估计函数的平均方差MSE 最小，MSE 可由下式求得［11］：

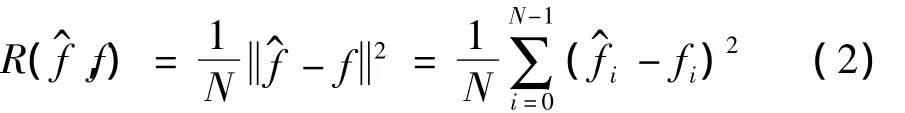
传统的阈值去噪方法采用以下三步［12］：

（1）对向量y进行离散小波分解［13］，得到第j层小波系数为uj，k，其中j=1，…，J；

（3）对上一步所得的小波阈值去噪后的小波系数进行离散小波重构，得原信号的估计函数。

在阈值去噪过程中，对信号进行小波分解后所得的小波系数中，太高的系数是原信号的细节，太低的系数一般来说都是噪声［8］，太高和太低的系数都不会产生误判断，而中间值域的细节可能和噪声差别不大，甚至湮没在噪声信号中，最容易被当作噪声误滤除掉。为减少原信号细节在去噪过程中的误判，在小波分解后，本文通过函数变换使易混淆值域的小波系数的差别放大，在阈值判定中的权重增大，然后选取阈值进行去噪，再通过变换函数的逆函数将小波系数恢复，最后小波重构获得去噪结果。

符合阈值去噪改进方法要求的变换函数应具有以下条件：

（1）在某一定义域［cmin，cmax］（cmin、cmax分别为小波系数中最小和最大的系数）中单调且连续，以对变换后的系数再进行反变换，恢复原信号。

（2）在定义域［cmin，cmax］中可导，且导数从较小逐渐增大，或者导数先增大再减小，这样才能使小波系数中间区域的系数差异增大，便于识别。

（3）导数（尤其是中间部分的导数）应大于1。

满足以上条件的函数较为典型的有以下两个函数

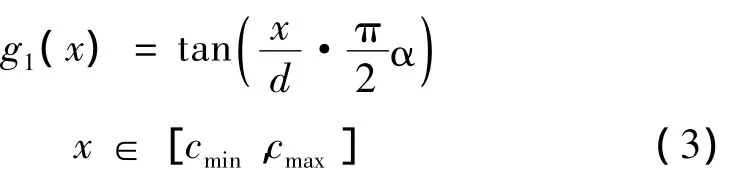
和：

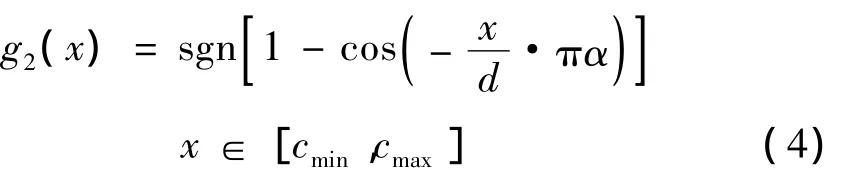
其中d=cmax－cmin，α为常数且α∈［0.6，1］，本文中取α=1。

g1（x），g2（x）在定义域中单调且连续，且中间部分导数较大，可以使得被变换的小波系数中间部分的差别被放大，从而在随后进行的阈值去噪可以将原信号的细节和噪声能够更好的区分开来，不至于将细节误滤掉。

小波系数阈值去噪之后，需要对小波系数进行后变换，即将小波系数代入变换函数的反函数中。对应于上面提到的g1（x），g2（x），其反函数分别为：

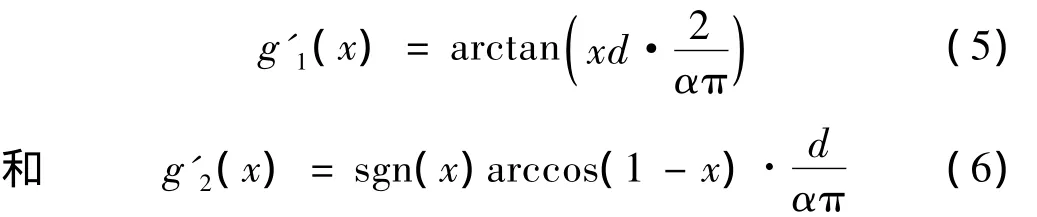
较传统阈值去噪方法，改进去噪方法主要增加了对小波系数的变换，其去噪步骤如下：

（1）对向量y进行离散小波分解得第j层小波系数uj，k，其中j=1，…J。

（2）将小波系数uj，k代入变换函数g（x）进行变换，得第j层小波系数uj，k’，其中j=1，…，J。

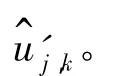
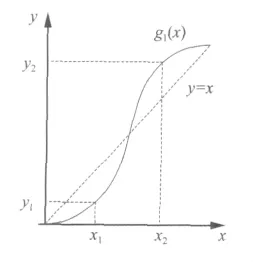
图1 改进函数示意图Fig.1 The improving function

（5）对进行离散小波重构得信号的估计。

其中第2步和第4步是本文对原阈值去噪算法改进后新增加的步骤。

2 仿真实验

为验证本文中所提出的方法，我们选取Donoho提出的函数HeaviSine进行测验［3］。选取信号长度均为1 024，信噪比SNR=10。采用的变换小波为Symlets6，分解层数J=5，变换函数采用式（4）中的g2（x）。

目前常用的阈值去噪方法：软阈值去噪、硬阈值去噪、Garrote阈值去噪和Semisoft阈值去噪。其函数表达式分别为：

软阈值去噪函数：

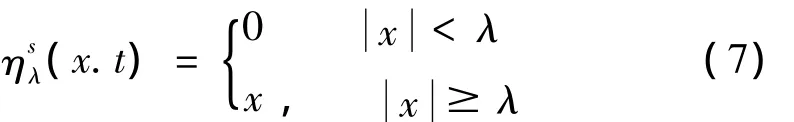
硬阈值去噪函数：

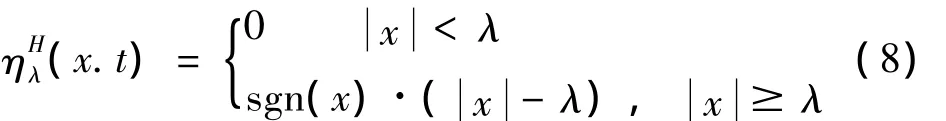
Garrote阈值去噪函数：

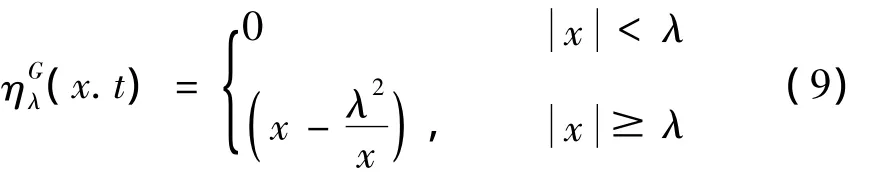
Semisoft阈值去噪函数：

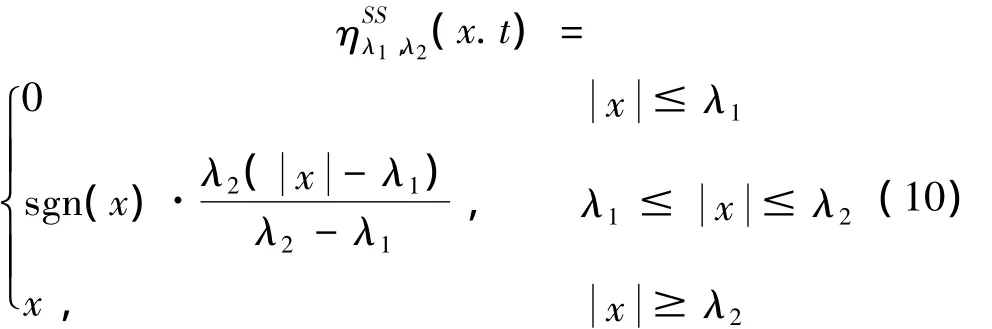
其中λ，λ1和λ2均为去噪阈值。

本文中阈值λ采用固定阈值（sqtwolog）的形式，方差由文献［14］中所述的改进的方差估计算法获得，此改进方法可以提高信噪比，同时减少运算时间。计算公式如下：

第j层小波系数阈值去噪采用的阈值为：

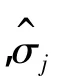
表1 仿真去噪后所得结果的SNR和MSE值Tab.1 SNR and MSE of the de-noised signal in simulation

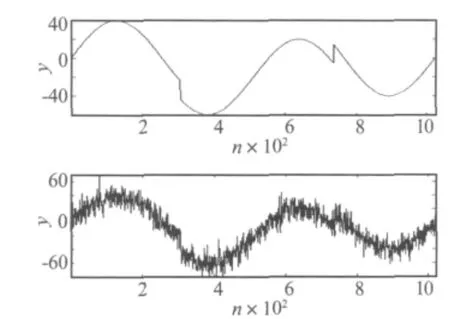
图2 原信号HeaviSine及其加噪信号（SNR=10）Fig.2 The original signal of Heavi Sine and its noisy signal

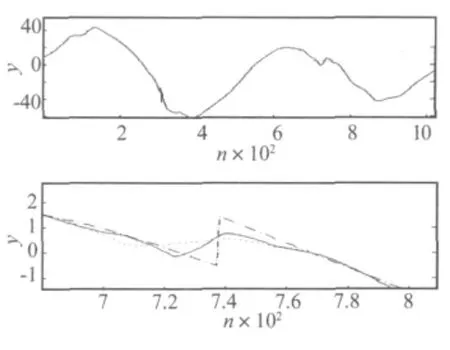
图3 软阈值去噪及其改进方法去噪效果对比图和局部放大图（…软阈值方法去噪；——改进软阈值法去噪；－·－原信号）Fig.3 The results of de-noising by soft threshold and its improved method and their partial enlarged view（…hard threshold；—— improved hard threshold；－·－the original signal）

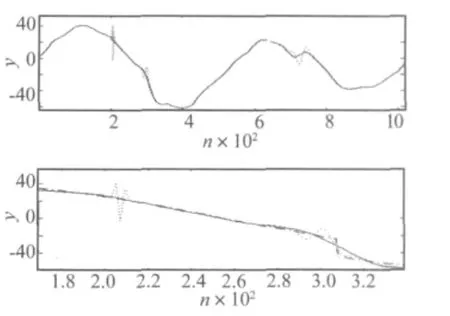
图4 硬阈值方法及其改进方法去噪效果对比图和局部放大图（…硬阈值方法去噪；——改进硬阈值法去噪；－·－原信号）Fig.4 The results of de-noising by hard threshold and its improved method and their partial enlarged view（…soft threshold；—— improved soft threshold；－·－the original signal）

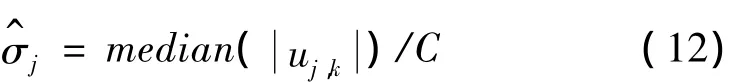
其中，uj，k是第j层小波系数值，median（*）表示计算中值，C为常数，一般取 0.674 5。

Semisoft方法需要两个阈值，本文中采用固定阈值（sqtwolog）和基于 Stein的无偏似然估计阈值（rigrsure）。

本文对同一仿真含噪信号分别使用上述四种去噪方法及相应的改进后的算法予以去噪，去噪结果如表1，其中SNR为信噪比，MSE为由公式（2）计算所得的平均方差。由表可见，从SNR，MSE两项去噪指标上来讲，改进方法对传统的去噪方法都有所改进，但对硬阈值去噪方法改进最为明显。另外，通过横向比较可见，前三种阈值去噪方法（软阈值方法，硬阈值方法，Garrote方法）改进后去噪效果基本一致，只有Semisoft去噪方法改进后与其他改进方法结果稍有偏差（这是因为Semisoft使用两个去噪阈值，这一点与其他三种方法不同）。结果表明，前三种去噪方法，使用本文所述方法改进后都可以改善SNR，MSE两项去噪指标。

对仿真含噪信号进行去噪后的结果表明阈值去噪改进方法对去噪结果均有较优改善：

（1）软阈值方法改进后（如图3），原信号中第737点处的突起更为明显，更能显示出信号的突变。

（2）硬阈值方法（如图4）和Semisoft阈值方法改进后，减少了原方法去噪后的Gibbs振荡。

（3）Garrote方法改进后去噪效果有一定的改善，但不太明显。

3 实验验证

为验证改进去噪算法，本文对噪声环境下伴有冲击的旋转电机的音频信号进行了采集，使用传统阈值去噪方法和改进算法对采集数据进行去噪，并比较去噪结果。选取微型电机FA130作为主要声源，另以扬声器产生高斯噪声，作为附加噪声源。电机额定转速19 400 r/min，实验时带负载，实际转速约为12 000 r/min。声音信号采集使用电容式麦克风isk800，AD转换使用数据采集卡NI USB－6251。利用Labview软件编程，控制采集过程，获得采样数据，然后使用基于本文所述的改进去噪方法的matlab程序进行分析。由于电机的工作频率（约200 Hz）以及敲击振动频率范围较广且大部分能量集中在低频的特点［15］，根据采样定理，实验中采样率设为1 000 Hz，采样点数为8192。音频信号采样过程中，在电机壳体上敲击两次（一强一弱）以得到冲击噪声，采集到的音频信号数据如图5。

分别使用传统阈值去噪方法和改进方法对音频信号进行去噪，结果显示改进去噪方法去噪效果更好。如图6和图7（在此以软阈值去噪和改进软阈值去噪法得到的处理结果为例），较为明显的是：两种方法都可以显示第一次冲击（第1 400个点附近），但是传统的软阈值去噪将第二次轻微的敲击信号误判为噪声予以了削弱，结果不能很好地显示第二次冲击（第6 000个点附近），而改进后的软阈值方法保留了冲击信号，可以较为明显的显示出第二次的冲击。对本实验数据分别用其他的传统阈值去噪方法及改进方法进行去噪处理后，去噪结果均显示改进方法较优。因此，本文提出的阈值去噪的改进方法，可以增强对含噪信号中某些较为细微信号的识别性（如较小的突变信号），且不增加伪Gibbs振荡。

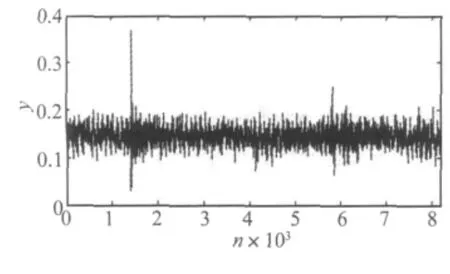
图5 电机音频信号采样结果Fig.5 The noise of the motor

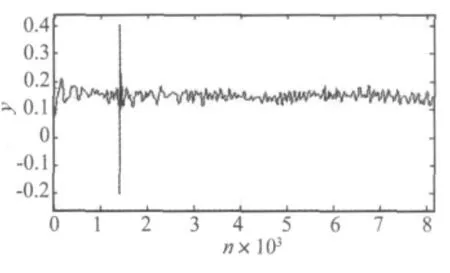
图6 音频信号软阈值去噪结果Fig.6 The results of de-noising by soft threshold

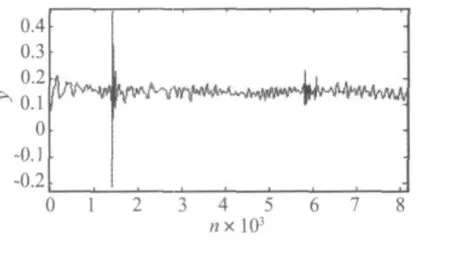
图7 音频信号软阈值去噪改进方法去噪结果Fig.7 The results of de-noising by the improved soft threshold

4 结论

阈值去噪改进算法将与噪声信号难以区分的值域中的小波系数差别放大、权重加大，以更好地确定小波去噪阈值，为解决小波阈值去噪过程中如何准确估计出合适的阈值这一关键问题提供了一条有效的途径。

阈值去噪改进方法经仿真和实验验证，能够比传统阈值去噪方法更好的去除高斯白噪声，保留原信号的细节特征，而且算法不太复杂，是比传统阈值去噪方法更为优越的去噪方法。

［1］Vetterl M，Chang S G，Yu B.Adaptive wavelet thresholding for image denoising and compression［J］.IEEE Signal Processing Letters，1998，5（10）：265 －267.

［2］ Donoho D L.De-noising by soft-thresholding［J］.IEEE Trans.Inform.Theory，1995，41：613 －627.

［3］Donoho D L，Johnstone I M.Ideal spatial adaptation via wavelet shrinkage［J］.Biometrika，1994，（81）：425 －455.

［4］Donoho D L， JohnstoneIM. Adaptingtounknown smoothness via wavelet shrinkage［J］.Journal of the American Statistical Assoc.，1995，90（432）：1200 －1224.

［5］ Donoho D L，Johnstone I M，Kerkyacharian G，et al.Wavelet shrinkage：Asymptopia?［J］.J.R.Stat.Soc.B，1995，57（2）：301－369.

［6］朱艳芹，杨先麟.几种基于小波阈值去噪的改进方法［J］.电子测试，2008，（2）：18 －22.

［7］曾守桢.小波去噪及其在信号处理中的应用［D］.天津：天津大学，2007.

［8］徐铮伟.小波阈值特征选取与去噪研究［D］.长春：吉林大学，2008.

［9］兰 芸.樊可清.基于小波阈值去噪方法的研究［J］.科技信息（科学教研），2008，（2）：209 －210.

［10］臧玉萍，张德江，王维正.小波分层阈值降噪法及其在发动机振动信号分析中的应用［J］.振动与冲击，2009，28（8）：57－60.

［11］唐进元，陈维涛，陈思雨，等.一种新的小波阈值函数及其在振动信号去噪分析中的应用［J］.振动与冲击，2009，28（7）：118－121.

［12］ Zhang X P，Desai M D.Adaptive denoising based on SURE risk［J］.IEEE Signal Processing Letters，1998，5（10）：265－267.

［13］ Rioul O，Duhamel P. Fast algorithms for discrete and continuous wavelet transforms［J］.IEEE Trans.Inform.Theory，1992，38：569 －586.

［14］李淑霞，王汝霖，李春梅，等.基于噪声方差估计的小波阈值图像去噪新方法［J］.技术机应用研究，2007，24（1）：220－221.

［15］何 闻，叶贵如，杨世超，等.冲击信号测量系统中下限频率的正确选取［J］.振动、测试与诊断，1994，14（3）：22－28.