永磁同步伺服系统速度调节器抗饱和补偿器设计

杨明， 李钊， 胡浩， 徐殿国

(哈尔滨工业大学电气工程系，黑龙江哈尔滨 150001)

永磁同步伺服系统速度调节器抗饱和补偿器设计

杨明， 李钊， 胡浩， 徐殿国

(哈尔滨工业大学电气工程系，黑龙江哈尔滨 150001)

针对永磁同步伺服系统速度调节器积分饱和问题，按照反计算思想，提出一种新型的AW设计方法。该AW方法可根据PI调节器输入输出状态确定反计算支路的增益，为其提供一套整定原则。通过仿真和实验对比传统反计算AW与该新型AW设计方法，仿真和实验结果验证了该新型AW设计的可行性及优越性。在保证系统响应速度的前提下，新型AW设计的PI调节器能有效降低系统动态响应的超调，特别是在大范围变化时，可综合提高系统的动态性能。

anti-windup;永磁同步电机;PI控制器;反计算

0 引言

在控制系统中，被控对象常存在各种各样的限制，如电机控制系统中，由于受到电动机最大电流、发热等因素的限制，需对电机电流给定值进行限幅。对于采用PI控制器的电机控制系统，这种限幅环节的存在，可能导致控制器输出与被控对象实际输入不等，进而引起系统闭环响应变差。这种由于输入限制的存在，而引起系统响应变差的现象被称为Windup现象［1］。在系统控制器的设计过程中，如果不考虑 Windup现象，会大大降低系统的整体性能［2－3］。

众多学者针对Windup现象进行大量而细致的研究，提出许多AW设计方法［4－7］，按AW作用机制可大致分为两大类［8］。一类方法采用条件积分技术，即存在一个开关环节，当系统控制器发生饱和限幅时，停止或限制控制器的积分作用。这种方法实现简单，但缺乏鲁棒性，一旦系统产生变化，该方法不一定能有效抑制Windup现象;另一种方法基于反计算思想，将控制器输出与被控对象限幅输入的差值作为负反馈，用以抑制Windup现象。这种方法中，通过合理配置负反馈支路增益可达到较为理想的控制效果，但对不同的系统条件同样缺乏鲁棒性。

本文在传统基于反计算思想AW设计的基础上，研究一种基于给定误差的分段反计算AW方法。与传统的反计算AW方法相比，该方法可根据系统运行状态对反计算环节的相关参数自动进行配置。通过与传统反计算AW设计在永磁同步伺服系统进行了对比仿真和实验。

1 传统AW设计

反计算跟踪(back calculation and tracking，BCAT)法是永磁同步伺服系统中最常用AW方法。

1.1 反计算跟踪AW的原理

任何相对慢时变环节的存在都会引起Windup现象［9］。对于PI控制器，Windup现象的产生往往由PI控制器的积分环节引起，因此消除Windup现象往往从抑制动态过程的积分作用入手。

图1为基于反计算思想的传统AW设计框图，在带限幅PI控制器的基础上，将(un－us)作为负反馈引入至积分环节。由该框图可推得PI控制器的输出为

式中:Kp为控制器比例系数;τi为控制器积分时间常数;τc为抗积分饱和补偿系数。

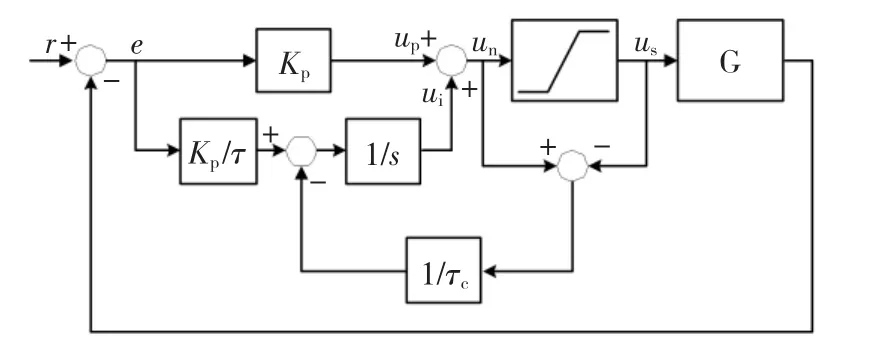
图1 传统反计算跟踪AW设计框图Fig.1 Classical BCAT AW structure

由该AW方法的原理可知，τc取值的大小对AW的效果有重要影响。根据经验公式，τc的取值范围在［(1 －8)τi］之间［10］。

对于图1所示的闭环控制系统，设us∈［－0.1，0.1］，Kp=1，在此基础上对基于反计算跟踪AW的永磁同步伺服系统进行建模仿真，给定阶跃速度指令r:0→1(“1”代表额定转速3 000r/min)时，不同τc下系统的仿真结果如图2所示。

反计算跟踪AW的算法结构简单明了，并且由图2的仿真结果可以看出，合理配置反馈补偿Kc(Kc=1/τi)可获得较理想控制效果，因此该方法在永磁同步伺服系统中被普遍采用。

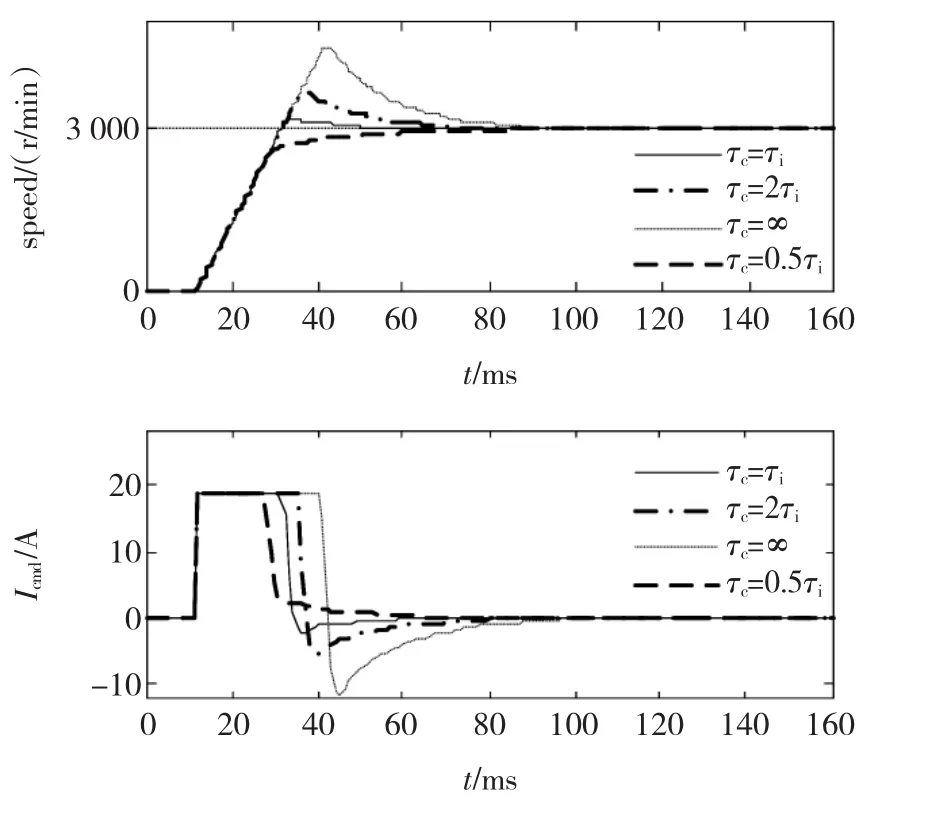
图2 传统反计算跟踪AW仿真Fig.2 Simulation of Classical BCAT AW

1.2 反计算跟踪AW的应用

如前所述，带限幅PI控制器内负反馈环节的引入，主要是为了消除动态过程中可能产生的积分饱和现象。在永磁同步伺服系统中，为了使电机获得快速响应并使系统具有较大的刚度，PI控制器往往具有较大的比例增益和积分系数。在系统给定大阶跃指令时，由于给定误差e和比例增益都很大，图2中控制器的输出us会瞬间达到饱和值，负反馈环节在产生积分饱和现象前即生效并产生退饱和作用。

对图1所示系统，当产生饱和时，误差积分ui的增大或减小取决于负反馈环节参数Kc(Kc=1/τc)的大小。如果ui进一步增大，则会造成系统的响应产生较大超调，如图2中τc=2τi曲线。为了避免系统在大动态过程中产生较大超调，可行的办法是增大 Kc即使 τc＜ τi，响应波形如图 2 中 τc=0.5τi曲线。

传统AW方法有一个明显的缺点，控制参数Kc需要人为配置且具有较大的不确定性。而且，即使对于某一固定阶跃给定时获得最佳响应的补偿系数Kc，也无法保证系统在所有运行状态下都有良好的速度响应。

基于反计算跟踪AW的永磁同步伺服系统，负载惯量不变的情况下，采用相同Kp、Ki(Ki=1/τi)、Kc(τc=0.7τi)控制参数，给定不同大小的阶跃速度指令时的仿真结果如图3所示。

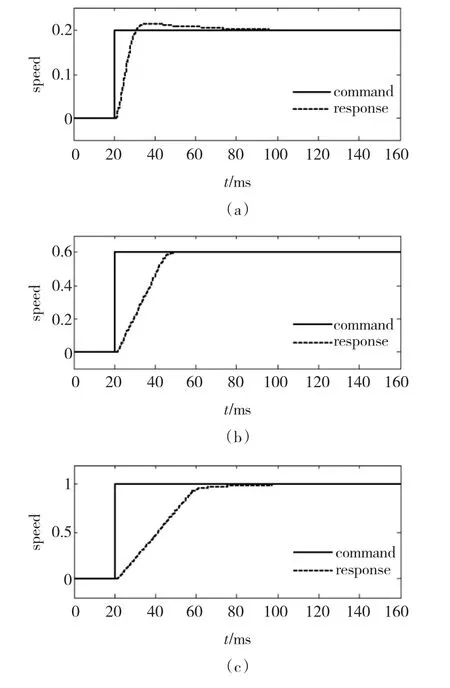
图3 反计算跟踪AW系统仿真响应Fig.3 Simulated performance of BCAT AW

由图3的仿真结果可以看出，采用同一套参数而给定不同大小的阶跃速度指令(r=0.2，0.6和1)，电机速度响应会有很大差别。图3(a)所示当给定速度较小时，由于饱和作用不明显因而AW算法作用影响小，造成系统出现较大超调;当给定速度适中时，饱和与退饱和作用相当，系统获得最为理想的阶跃响应，如图3(b);而在速度阶跃更大时，由于退饱和负反馈环节的作用强度和时间都增大，图3(c)的电机速度响应会出现提前退饱和现象，造成过渡时间加长。如果系统最高转速可以大于额定转速时，提前退饱和现象将更为明显。

实际PMSM系统上的响应情况如图4所示，阶跃速度指令不同时系统响应同仿真结果一样，AW补偿不能实现对所有给定指令的优化响应。

由仿真和实验结果可知，在采用传统反计算跟踪AW的永磁同步伺服系统中，在电机负载转动惯量等外部环境因素保持不变的情况下，即使同一套控制参数(Kp、Ki、Kc)在不同给定指令下的响应也会有很大差别。由于给定指令不同，造成电机动态运行过程中控制器的饱和深度和饱和持续时间都有所不同，反馈补偿环节的作用强度也会随之变化。这就造成了当给定阶跃较小时系统出现明显超调，而当阶跃给定很大时，系统响应出现提前退饱和现象。传统的反计算跟踪AW方法无法克服这一缺陷。

图4 反计算跟踪AW系统实验响应Fig.4 Experimental performance of BCAT AW

2 分段反计算AW

在传统反计算跟踪AW方法的基础上，提出一种基于给定误差的分段反计算AW方法。由前述分析可知，固定不变的AW补偿系数Kc其效果并不理想。因此本文所提出的基于给定误差的分段反计算AW方法:可根据控制系统的实际运行状态，对控制器的补偿系数Kc进行自动调整，即可保证系统的快速响应，又可避免大阶跃给定下系统响应出现大幅度超调或提早退饱和现象。

对图1 所示系统，仍假设 us∈［－0.1，0.1］，Kp=1，给定阶跃指令r:0→1，则控制器输出瞬间饱和即un＞us＞0。令 eu=un－us，如果在控制器产生饱和时使负反馈增益满足式(2)，则控制器积分输出ui保持不变，即

设初始状态ui(0)=0，按式(2)选取Kc可保证在控制器饱和期间积分输出ui(t)=0，则

将式(3)代入式(2)有

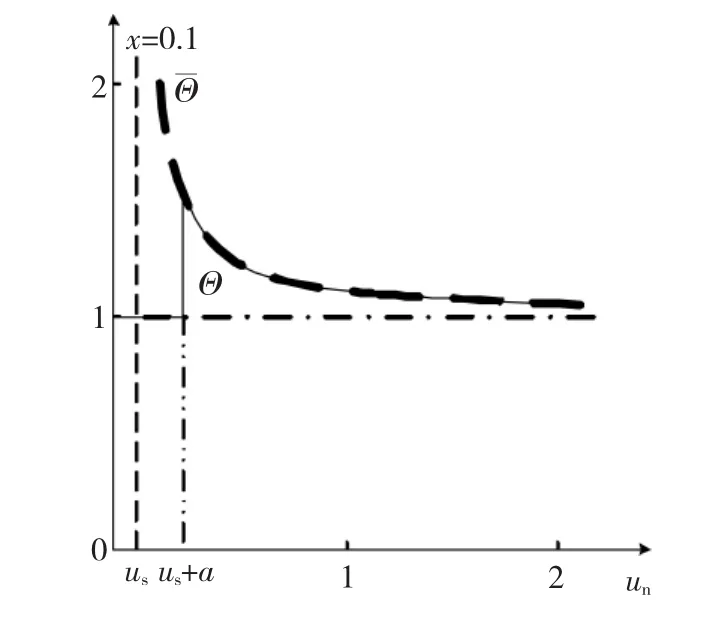
图5 反馈支路增益调整曲线Fig.5 Gain function of the feedback branch

如果Kc/Ki严格按照函数珚Θ选取，控制器一旦发生饱和，积分作用会完全停止，此时控制器的AW机制与条件积分方法等效。

在PMSM系统的实际应用中，尤其是在电机负载较大时，对积分作用进行过度抑制会导致电机速度响应变差，如图6所示。控制器产生饱和时，为了避免电机速度上升到稳态值前控制器产生提前退饱和现象，在防止控制器过度积分的前提下，还必须对积分过程予以一定程度的保留。

图6 积分受限条件下系统的响应Fig.6 System response with integral limited

现设定一阈值常数a，用以表征控制器的饱和深度。当eu=un－us≥a时，控制器处于深度饱和状态，按式(2)确定Kc以对积分作用进行抑制;而当0＜eu=un－us＜a时，令 Kc=Ki，此时控制器 AW 机制与传统反计算跟踪AW相同。由此确定负反馈增益Kc的调整原则为

在函数Θ中，变量包含给定误差e及控制器输出un，函数Θ曲线如图5中实线所示。至此，可确定基于给定误差的分段反计算AW设计框图如图7所示。

图7 分段反计算AW设计框图Fig.7 Segmented Back Calculation AW structure

当系统阶跃给定较小时，PI控制器输出un＜us+a，此时分段反计算AW与传统反计算跟踪AW效果相同，控制系统阶跃响应有一单峰值超调。

在系统空载条件下，调整a值以保证系统的阶跃响应有5%左右的超调，则系统带载时，系统超调可得到明显的吸收，达到理想的控制效果［11］。一旦a值确定，控制器即可根据系统运行状态自动对负反馈增益Kc进行在线调整，而无需人为对其进行设定。

3 仿真和实验

仿真和实验中所使用的永磁同步伺服系统，参数为:额定功率750 W，额定转矩2.4 N·m，额定转速3 000 r/min，定子电阻0.45 Ω，定子电感3.9 mH，最大定子电流18.6 A。

图8为永磁同步伺服系统在空载条件下，给定阶跃速度指令r:0→0.2及r:0→1，分别采用传统反计算跟踪AW和基于给定误差的分段反计算AW时的仿真结果。

由图8的仿真结果可以看出，系统的PI控制器在采用分段反计算AW设计后，对于大阶跃指令，即能有效抑制系统响应超调，又能避免传统反计算AW法中补偿系数不合理造成控制器提前退饱和;对于小阶跃指令，由于控制器在动态过程未达到饱和阈值a，此时PI控制器的AW机制与传统AW相同，故二者响应相同。

对采用分段反计算AW设计的永磁同步伺服系统，分别在空载和带载条件下进行系统仿真，其仿真结果如图9所示。

图9 不同负载条件下反计算跟踪AW系统仿真Fig.9 Simulation of Segmented Back Calculation AW structure under different load conditons

图9的仿真结果表明，采用分段反计算AW设计的永磁同步伺服系统在带载条件下，其阶跃响应的略微超调能得到明显抑制，且没有出现图6所示等效条件积分AW法带载条件下响应变差的现象。

在实际PMSM系统平台上，分别做如上对比实验，其实验结果如图10、图11所示。其实验结果与仿真相符。

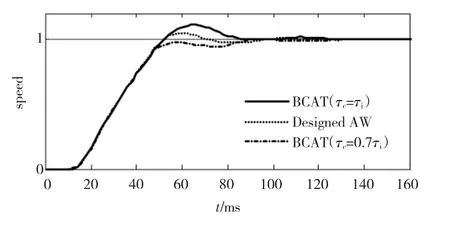
图10 不同AW系统实验响应Fig.10 Experimental performance of different AW system

图11 不同负载条件下反计算跟踪AW系统仿真Fig.11 Experimental of Segmented Back Calculation AW structure under different load conditons

4 结语

对于永磁同步伺服系统，本文基于给定误差的分段反计算AW设计，解决了传统反计算跟踪AW设计中控制参数配置匹配困难的问题，在保证电机快速响应的同时，能有效抑制大动态范围内系统响应的超调并可避免因参数设置不当导致控制器提前退饱和，为系统提供良好的动态品质。

［1］ PENG Youbin，VRANCIC Damir，HANUS Raymond.Anti-windup，bumpless，and conditioned transfer techniques for PID controllers［J］.IEEE Control Systems Magazine，1996，16(4):48－57.

［2］ ZHANG Da，LI Hui，EMMANUEL G Gollin.Digital anti-windup PI controller for variable-speed motor drives using FPGA and stochastic theory［J］.IEEE Transactions on Power Electronics，2006，21(5):1496 －1501.

［3］ GUIDO Herrmann，TURNER M C，GUO Guoxiao.Practical implementation of a novel anti-windup scheme in a HDD-dual-stage servo system［J］.IEEE/ASM Transactions on Mechatronics，2004，9(3):580 －592.

［4］ SYAICHU-ROHMAN A，MIDDLETON R H.Anti-windup schemes for discrete time systems:an LMI-based design［C］∥Control Conference.Melbourne，Australia:IEEE，2004，1:554－561.

［5］ LAMBECK S，SAWODNT O.Design of anti-windup-extensions for digital control loops［C］//Proceedings of the 2004 American Control Conference.Boston，USA:IEEE，2004，6:5309 －5314.

［6］ CUPERTINO F，MININNO E，NASO D，et al.On-line genetic design of anti-windup unstructured controllers for electric drives with variable load［J］.IEEE Transactions on Evolutionary Computation，2004，8(4):347－364.

［7］ PHIL March，Matthew C Turner.Anti-windup compensator designs for nonsalient permanent-magnet synchronous motor speed regulators［J］.IEEE Transactions on Industry Application，2009，45(5):1598－1608.

［8］ 杨明，徐殿国，贵献国.控制系统Anti-Windup设计综述［J］.电机与控制学报，2006，10(6):622－625.

YANG Ming，XU Dianguo，GUI Xianguo.Review of control system anti-windup design［J］.Electric Machines and Control，2006，10(6):622－625.

［9］ DOYLE J C，SMITH R S，ENNS D F.Control of plants with input saturation nonlinearities ［C］//America ControlConference.1987:1034－1039.

［10］ ASTROM K J，HAGGLUND T.PID Controllers:Theory，Design，and Tuning［M］.2nd ed.Instrument Society of America，1995.

［11］ 杨明，高扬，于泳，等.基于迭代学习控制的交流伺服系统PI参数自整定［J］.电机与控制学报，2005，9(6):588－592.

YANG Ming，GAO Yang，YU Yong，et al.On-line self-tuning of PI controller for PMSM drives based on the iterative learning control［J］.Electric Machines and Control，2005，9(6):588 －592.

(编辑:于智龙)

Anti-windup design for PI regulator of PMSM servo system

YANG Ming， LI Zhao， HU Hao， XU Dian-guo

(Department of Electrical Engineering，Harbin Institute of Technology，Harbin 150001，China)

Aiming at the problem caused by the PI integral saturation of speed regulator in permanent magnet synchronous servo system，a novel anti-windup(AW)design which is based on the mind of backcalculation was presented.The proposed AW design provided a tuning principle for the back-calculation gain，which is determined according to the input and output status of PI regulators.The new method of AW was compared with the classical AW by simulation and experiment.The simulated and experimental results demonstrate the feasibility and advantage of the new AW design.The PI regulator with the proposed AW design can reduce the overshoot of system dynamic response with the similar response speed，and improve the dynamic behavior especially in wide range of dynamic variation.

anti-windup;permanent magnet synchronous motors;PI controller;back-calculation

TN 911.22

A

1007－449X(2011)04－0046－06

2010－11－26

国家自然科学基金(51007012);哈尔滨工业大学优秀青年教师培养计划(HITQNJS.2009.026)

杨 明(1978—)，男，副教授，研究方向为交流伺服系统与智能控制;

李 钊(1986—)，男，硕士研究生，研究方向为永磁同步伺服系统驱动控制;

胡 浩(1987—)，男，硕士研究生，研究方向为交流伺服系统;

徐殿国(1960—)，男，教授，博士生导师，研究方向为电力电子与电力传动、电机驱动控制、电网统一品质控制。