力控制系统的若干设计问题

刘彦文， 王广雄， 李佳， 綦志刚

(1.哈尔滨工程大学自动化学院，黑龙江哈尔滨 150001;2.哈尔滨工业大学航天学院，黑龙江哈尔滨 150001)

力控制系统的若干设计问题

刘彦文1， 王广雄2， 李佳1， 綦志刚1

(1.哈尔滨工程大学自动化学院，黑龙江哈尔滨 150001;2.哈尔滨工业大学航天学院，黑龙江哈尔滨 150001)

提出各类力控制系统设计时应遵循的原则。分析指出力控制中的对象数学模型是零阶的比例环节，所以系统的回路中必定要包含一个积分环节以保证带宽。故在一般的工业应用场合，力控制系统常采用一种比例的速率控制模式。在机械手的力控制中则是采用积分控制律。由于积分控制的动态响应较慢，所以系统设计中还常包括对扰动的补偿。对于阻抗控制场合，力控制设计应该与期望的虚拟环境的阻抗相匹配。此外，为了保证人在回路实时控制系统的稳定性，应该进行无源性设计。所提出的设计原则对系统的调试也极有帮助。

力控制;速率控制;积分控制律;阻抗控制;无源性设计

0 引言

一般提到机械运动的控制往往只是想到伺服控制，用伺服系统位置控制的概念来理解和考虑问题，不过随着生产技术的发展，出现了不少新的控制问题，光用伺服设计的概念已经不能满足实际设计的需要。这些新出现的控制问题之一是关于力的控制。在20世纪90年代，力控制还主要是机械手控制中的问题，这些年来很多工业应用领域都提出了力控制的要求，例如汽车和机车制动系统中制动力(力矩)的控制［1－2］，起重或拖曳作业中力的控制［3－4］，主动减震系统中力的控制［5－6］，飞行模拟器等各种仿真和遥操作系统中的力控制问题(阻抗控制)［7］等等。虽然涌现出了众多力控制的实例，但是在文献中都是作为某种新理论/方法的一种应用例题来报导的，例如反步法设计［1］，无模型控制［4］等，都没有对力控制系统的基本组成问题进行正面的阐述。其实力控制系统的设计有其本身的特点，正确掌握其特殊性将有利于系统的设计和调试，也有利于与采用力控制有关的新理论/方法的实质性的了解。下面将从系统设计的角度来对力控制问题进行归类和说明。

1 力控制中的对象模型

力控制问题中的对象模型一般都用图1的质量－弹簧－阻尼系统来描述，其传递函数为

图1 对象模型Fig.1 Plant model

不过式(1)只是理论研究时用的模型，实际应用时都把这对象看做是一个比例环节，即加力时就有一定的形变，G(s)=1/k，模型中k的取值一般大于10 kN/m，由于对象是比例环节，当组成系统时，为保证系统具有指定的带宽，控制规律中一定要包含积分环节［8］。有些文献中不加讨论笼统地归结为PID控制，那是不合适的。应该明确需要采用积分规律，这才能压低系统的幅频特性，并在指定的工作频段上穿越0dB线。本文就是基于这样的认识来讨论力控制系统的设计问题的。

2 一般应用中的力控制

力控制中的对象具有比例特性，即力的变化与位移变化量是成比例的。位移与速率之间是一种积分关系，这个速率的积分关系可以归入到对象，而使对象成为一个积分环节。这时对象的输入是速率，

进行控制，如图3所示。但是实际上图3的方案中对电机的速率ω是无法直接进行控制的，故ω称为虚拟控制。文献［1］主要是围绕着这个问题，用反步法一步一步地反推到对磁阻电机的力矩控制，使最终的系统特性逼近到图3用虚拟控制时的特性。文献［1］主要是讨论磁阻电机的反步法控制设计问题，其实这个系统的核心是图3的(比例的)速率控制，系统的设计就是在这个基础上来展开的。这也就是本文想传达的力控制系统的设计思想。而控制律就可以采用比例控制，即采用比例的速率控制，也可达到上面所说的积分控制的效果。一般工业中应用的力控制系统都采用这样的系统结构。这是因为力控制都需要某种执行机构来实施，而执行机构的速率工作模式是最容易实现的，而且这时的控制律也只要求是比例控制。当然对于一些较为复杂的系统，这速率模式可能需要用一个速率回路来实现。下面通过几个力控制的实例来作进一步的说明。

实例1 刹车片的力控制

图2是一个采用磁阻电机(switched reluctance motor，SRM)的机电式汽车制动系统［1］，图中 Fref是制动系统所要求的制动力。SRM通过蜗轮蜗杆传动压紧刹车片产生制动力。施加在刹车片上的力F与磁阻电机的转角θ之间是一种非线性函数关系，F=μF(θ)，而且这个函数关系在上下限之间存在一定的不确定性，所以该制动系统要采用反步法(backstepping)来进行设计。反步法的第一步是定义一个虚拟控制量ω对一个一阶对象

图2 机电制动系统夹紧力控制结构Fig.2 Block diagram of the clamping-force controller in an electromechanical brake system

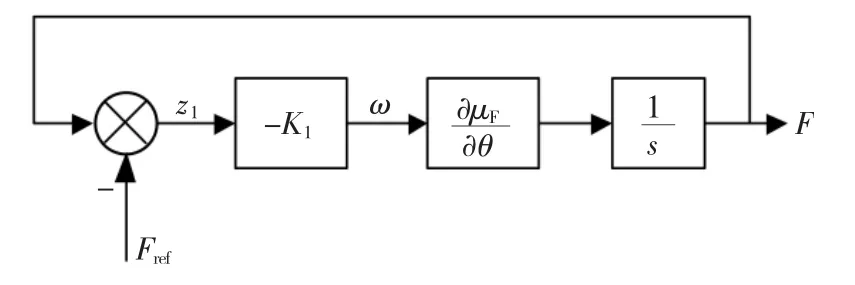
图3 反步法设计的第一步Fig.3 The first step of the backstepping design

实例2 主动悬挂系统中的力控制

为了提高乘坐的舒适性，现在提出对汽车的悬挂系统采用主动控制［6］。图4是主动悬挂系统的模型。图5是其力控制系统的框图［5］，图中Fd是悬挂系统设计所要求的控制力［6］，Fa是油缸上实际所给出的力，KLC是力传感器的系数(0.001 25 V/N)，Csp为滑阀的流量系数，α是与流体供给压力和排气压力差有关的系数，Bm是流体体积模数，V0是流体空间容积初始值，Ap是执行机构活塞面积。

图4 主动悬挂系统模型Fig.4 Active suspension system

图5 力控制系统框图Fig.5 Block diagram of the force control system

因为这个系统是通过流量的变化改变压力，对象中就包含一个积分特性(图5)，所以该系统的力控制规律就采用比例控制。图5中的Kf为伺服阀的比例系数，也就是比例控制器的增益，本例中Kf=5 ×10－4m/V。

对于图5的主动悬挂力控制系统，由于系统中存在干扰信号，所以有时还需在比例力控制的基础上加入干扰的前馈补偿。

实例3 水下拖曳升沉补偿系统的设计［4］

图6是一水下拖曳系统的示意图，系统由拖缆绞车，拖缆和拖体组成。拖曳作业时水面上拖船航速和升沉的波动将使拖体的深度出现变化，所以要设计一升沉补偿系统，通过对拖缆绞车的收放来保持恒定的深度。文献［4］主要讨论了非参数自适应控制在这种升沉补偿中的应用，其控制率为

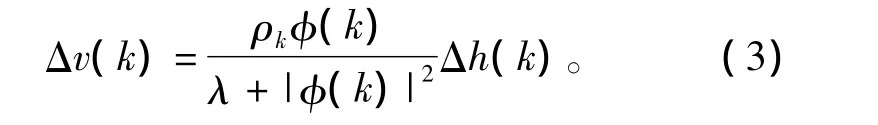
式中Δv为拖缆绞车收放速度的变化，Δh为拖体深度的变化，其他参数是自适应控制算法中的各有关参数。从式(3)可见，该自适应控制算法也是在速率控制的大前提下来展开的。

图6 水下拖曳系统示意Fig.6 Schematic diagram of an underwater towed system

文献［3］报道了另外一种钢丝绳力控制的实例。这是通过钢丝绳的悬吊减轻一部分体重，让中风病愈的患者练习走路。这里的力控制是通过对电机的速率控制来控制钢丝绳一端的拉力。由于钢丝绳的横向运动是不能控制的，即存在未建模动态，所以钢丝绳的比例的速率控制系统的带宽不能设计得太宽，约1～2 Hz左右，故如果系统的扰动较大，则尚需对扰动进行补偿［9］。

3 机械手的力控制

对机械手来说，各个关节都是一种位置工作模式，力控制时不能像上一节工业应用的场合可以采用速率工作模式。所以力控制时的对象特性是一种位移(变化量)与力之间的比例关系。因此机械手的力控制系统的控制律一定要用积分控制。有时也会笼统地说用PID控制，但是如果清楚知道起主要作用的是积分规律，那么对系统的调试就会容易的多。关于机械手的力控制在20世纪90年代有过大量的报告［10－11］，所以这里仅举一例来说明这种力控制系统的基本构成和特点。

实例4 机械手力控制之例［11］

图7描述了机械手所接触的环境表面的动态模型，是一个质量－弹簧－阻尼系统。

假定机械手在位置xs处与接触表面接触上，定义机械手末端与环境接触平面的内法线方向为n，设f是机械手施加在接触表面上的力，这个f沿着n方向的分量为fn，由于这个fn的作用，接触表面在n方向上会发生位置变形εn。这个n方向是受限运动方向，需要对这个方向的接触力进行控制，而与n方向垂直的p向(n方向的正交补方向)，是自由运动方向，无须进行力控制，只进行位置控制，所以是一种混合位置/力反馈控制。

图7 环境的动态Fig.7 The dynamics of the environment

图8为混合位置/力反馈控制结构框图，图中xdp=xcp和xp分别表示p方向的期望位移和实际位移，xdn和fdn分别表示n方向的期望位移和期望力给定值，xsn为环境表面的初始位置;图中1/s·Gf(s)为力控制器，Gs(s)为环境的传递函数，本例中等于比例常数ks，ks=10 kN/m。Gp(s)为包含位置控制器的机械手传递函数部分，是由图9所描述的给定位移xc到位移x的传递函数，根据图9可推导得Gp(s)为一个单位矩阵。

图8 混合位置/力控制系统框图Fig.8 The block diagram of the hybrid position/force control system

图9 带位置控制器的机械手框图Fig.9 The block diagram of the manipulator with the position controller

从图8可以看到，力控制回路的控制器有一个基本的积分环节。图中的Gf(s)可根据带宽要求来确定。

4 阻抗控制

控制问题中还有一种力控制的形式，就是阻抗控制。这是指出现运动时要产生一定的力，或者说，具有一定的阻抗。就像电路中电流通过阻抗产生压降一样，这里将速度与产生的力之间的关系称为(机械)阻抗Z。Z－1就相当于从力到速度之间的传递函数。例如，设手柄的质量为M，设运动无阻尼，则阻抗ZM=Ms。 (4)

阻抗控制广泛应用于各种飞行模拟器中，为受训练者提供操作时的虚拟环境［12］。各种遥操作机械手也需要用阻抗控制来提供逼真的作业环境，例如文献［7］中的遥操作铲车做到了能够在操纵杆上感受到现场作业时铲斗所遇到的同样的阻抗特性。

图10所示就是这样一种提供虚拟操作环境的装置，称为力觉接口(haptic interface)［13］。图 11 为系统的框图，图中fh是操作者施加在操纵手柄上的力，操作者手中感受到手柄的速度变化时就会自动调整施加在手柄上的力，这是一种负反馈的过程，图中用Zh代表人的这种生物机械阻抗(biomechanical impedance)特性［14］。图11中C(s)为力觉接口的控制器，一般均用PD控制，即

所以从fh到v的传递函数为

也就是说，传递到人手的阻抗是

将式(4)、式(5)代入后得

式中B，K为设计参数，可以根据要求的阻尼和刚度来进行选择。

图10 力觉接口的原理图Fig.10 Schematic diagram of the haptic interface

图11 力觉接口系统框图Fig.11 Block diagram of the haptic interface

式(7)的Z就是这个力觉接口所代表的虚拟环境。有些工作往往只根据所假设的(虚拟)环境来设计力觉接口的控制器C(s)，这是不够的。因为这个Z－1与操作者的阻抗Zh构成的是一个反馈回路，这里就有稳定性问题了。这时就不能单从控制器C(s)上来找问题。由于人的特性存在一定的不确定性，包括还可能出现一些操作不当的因素，所以对于这种有人参与的阻抗控制系统，宜采用无源性控制，即这个接口系统除了刚度等参数应满足操作时的虚拟环境的要求外，还应该将这个系统设计成一个无源系统［13－15］。这是因为作为操纵手的人的特性可视为是无源系统［13－14］，如果再将这里的阻抗系统也设计成无源系统，那么根据无源性定理［16－17］，两个无源系统的反馈连接，系统必定是稳定的。

5 结论

对于力控制来说，无论是通过速率控制或位移控制，力控制回路中一定要有而且也只有一个积分环节以保证系统的带宽。即使是采用各种其他的控制算法，也一定是在这样的系统结构上来展开的。认识到这一点，对于系统的调试来说，也将会容易和顺利得多。由于积分控制的速度较慢，即带宽较窄，所以力控制系统还常配有扰动补偿。

对于阻抗控制来说，力觉接口的设计不能仅满足虚拟环境的阻抗要求，还应考虑到操作者的阻抗特性，满足无源性的设计要求。

［1］ KRISHNAMURTHY L W，KHORRAMI F，KEYHANI A.Robust force control of an SRM-based electromechanical brake and experimental results［J］.IEEE Transactions on Control Systems Technology，2009，17(6):1306 －1317.

［2］ PARK S H，KIM J S，CHOI J J，et al.Modeling and control of adhesion force in railway rolling stocks［J］.IEEE Control Systems

Magazine，2008，28(5):44－58.

［3］ GLAUSER M，LIN Z，ALLAIRE P E.Modeling and control of a partial body weight support system:an output regulation approach［J］.IEEE Transactions on Control Systems Technology，2010，18(2):480－490.

［4］ 王海波，王庆丰.水下拖曳升沉补偿系统的非参数模型自适应控制［J］.控制理论与应用，2010，27(4):513－516.

WANG Haibo，WANG Qingfeng.Nonparametric model adaptive control for underwater towed heave compensation system ［J］.Control Theory＆ Applications，2010，27(4):513－516.

［5］ THOMPSON A G，DAVIS B R.Technical note:force control in electrohydraulic active suspensions［J］.Vehicle System Dynamics，2001，35(3):217 －222.

［6］ GAO H，SUN W，SHI P.Robust sampled-data H∞control for vehicle active suspension systems［J］.IEEE Transactions on Control Systems Technology，2010，18(1):238 －245.

［7］ SALCUDEAN S E，HASHTRUDI Z K，TAFAZOLI S，et al.Bilateral matched impedance teleoperation with application to excavator control［J］.Control Systems Magazine，1999，19(6):29 －37.

［8］ 王广雄，何朕.控制系统设计［M］.北京:清华大学出版社，2008.

［9］ 何朕，王广雄.悬吊减重系统的力控制［J］.电机与控制学报，2010，14(11):82－87.

HE Zhen，WANG Guangxiong.Force control of a partial weight support system ［J］.Electric Machines and Control，2010，14(11):82－87.

［10］ VOLPE R，KHOSLA P.A theoretical and experimental investigation of explicit force control strategies for manipulators［J］.IEEE Transactions on Automatic Control，1993，38(11):1634－1650.

［11］ OHTO M，MAYEDA H.A hybrid position/force control for robot manipulators with position controllers［C］//International Conference on Industrial Electronics，Control and Instrumentation，Oct.28 －Nov.1，Kobe，Japan.1991:1037 －1042.

［12］ 石旭东，张发，荆涛，等.飞行模拟机电动操纵负荷系统控制与仿真［J］.电机与控制学报，2010，14(5):73－78.

SHI Xudong，ZHANF Fa，JING Tao，et al.Control and simulation of electric control loading system of flight simulator［J］.E-lectric Machines and Control，2010，14(5):73 －78.

［13］ COLGATE J E，SCHENKEL G.Passivity of a class of sampleddata systems:application to haptic interfaces［J］.Journal of Robotic Systems，1997，14(1):37 －47.

［14］ LEE K，LEE D Y.Adjusting output-limiter for stable haptic rendering in virtual environments［J］.IEEE Transactions on Control Systems Technology，2009，17(4):768 －779.

［15］ FARDAD M，BAMIEH B.A necessary and sufficient frequency domain criterion for the passivity of SISO sampled-data systems［J］.IEEE Transactions on Automatic Control，2009，54(3):611－614.

［16］ KOKOTOVIC'P V，ARCAK M.Constructive nonlinear control:a historical perspective［J］.Automatica，2001，37(5):637－662.

［17］ VAN DER SCHAFT A.L2-gain and passivity techniques in nonlinear control［M］.Springer，2000.

(编辑:刘素菊)

Design problems of force control systems

LIU Yan-wen1， WANG Guang-xiong2， LI Jia1， QI Zhi-gang1
(1.College of Automation，Harbin Engineering University，Harbin 150001，China;2.School of Astronautics，Harbin Institute of Technology，Harbin150001，China)

The guidelines of the design for various force control systems are proposed.It is pointed out that the mathematical model of the plant in force control is of zero-order，so the system must include an integrator in its loop to ensure a limited bandwidth.Therefore，in the general industrial applications，the force control is often implemented with the proportional speed control mode.And for the manipulator applications，an integral control law is often needed for the force control.Because the dynamic response of the integral control is rather slow，so an addition disturbance compensation is often included in the design.For the impedance control cases，the force control design must match the desired impedance of the virtual environment.Besides，a passivity design is also needed to ensure the stability of a man-in-loop real-time control system.The proposed guidelines of the design are also helpful for tuning of the force control systems.

force control;speed control;integral control law;impedance control;passivity design

TP 273

A

1007－449X(2011)04－0098－05

2010－10－24

黑龙江省博士后科研启动金资助项目(LBH－Q09126);哈尔滨工程大学校基础研究基金资助项目(HEUFT07008，HEUFT08018);中央高校基本科研业务费专项资金(HEUCF100422);黑龙江省自然科学基金资助项目(F200803);黑龙江省博士后基金资助项目(LBH－Z07182，LBH －Z08246)

刘彦文(1976—)，女，博士，副教授，硕士生导师，研究方向为采样系统和鲁棒控制系统设计;

王广雄(1933—)，男，教授，博士生导师，研究方向为H∞控制，控制系统的鲁棒设计;

李 佳(1981—)，男，硕士研究生，研究方向为采样系统的鲁棒控制;

綦志刚(1976—)，男，博士，讲师，研究方向为船舶控制系统。