自适应滤波器的新型变步长算法及其应用

王新

(河南理工大学电气工程与自动化学院，河南焦作 454003)

自适应滤波器的新型变步长算法及其应用

王新

(河南理工大学电气工程与自动化学院，河南焦作 454003)

针对变步长算法的选取对自适应滤波器的性能有重大的影响，而常见变步长算法的步长与误差或输入信号有关，在自适应调节过程中步长存在较大的波动，影响自适应滤波器的滤波效果等问题，通过分析和比较常见的变步长算法，提出一种新型变步长算法。该算法先将误差信号取绝对值，然后再求其均值，以该均值决定步长的变化，克服步长波动的不足。采用新型变步长算法的自适应滤波器，不仅具有较快的收敛速度，而且可以获取较小的均方误差。最后，将基于新型变步长算法的自适应滤波器应用于笼型异步电动机的断条故障诊断中。实验证明，新型变步长算法可以增强断条故障的特征，有利于信号特征的提取。

自适应滤波器;变步长算法;转子断条;故障检测

0 引言

自适应滤波器以其优良的滤波效果，应用广泛。自适应滤波器的常用算法是最小均方算法。该算法具有方法简单、计算量小、易于实现实时处理等优点。由于均方误差与自适应步长成正比，然而步长减小，收敛时间增大。因此，在最小均方算法的权系数递推中常采用变步长代替固定步长，即变步长最小均方算法。这样，当权系数远离于最佳权系数，使用较大的步长，加速收敛速度;当权系数接近于最佳权系数时，使用较小的步长，获取较小的均方误差。在变步长最小均方算法中，变步长算法的选取十分关键，它对自适应滤波器的滤波效果有重大的影响［1］。目前，文献［2－3］提出的变步长算法应用较广泛。在自适应滤波器中，参考输入信号x(k)是幅值固定的余弦信号，误差ε(k)在自适应调节过程中是衰减振荡的，而当自适应调节过程趋于稳定时，ε(k)近似为幅值固定的交变信号。如果实际输入信号d(k)只含2个频率分量，那么自适应调节过程趋于稳定时，ε(k)近似为正弦信号。由于文献［2－3］中步长变化算法的步长μ(k)与ε(k)或x(k)有关。所以，在自适应调节过程中，尽管步长μ(k)是衰减的，但是它存在较大的波动，这对自适应滤波器的滤波效果有较大的影响。

为此，本文针对自适应调节过程中ε(k)和x(k)的变化规律，提出了一种新型变步长算法，它可以克服上述方法步长μ(k)上下波动的不足，不仅具有较快的收敛速度，而且当权系数接近最佳权系数时，具有较小的步长，获取较小的均方误差。最后，本文将新型变步长算法应用于笼型异步电动机的断条故障诊断中，验证了新型变步长算法良好的效果。

1 自适应滤波器的工作原理

自适应滤波器的工作原理如图1所示。图中，d(t)为原始输入信号，x(t)为参考输入信号，其中x(t)=Ccos(ω0t)，式中C为参考信号的幅值，ω0为待陷波的干扰正弦波的频率。d(k)、x1(k)、x2(k)分别为d(t)、x1(t)、x2(t)在kT时刻(T为采样周期)的采样值，w1(k)、w2(k)为权值采样值，ε(k)=d(k)－y(k)，其中y(k)为滤波器输出。

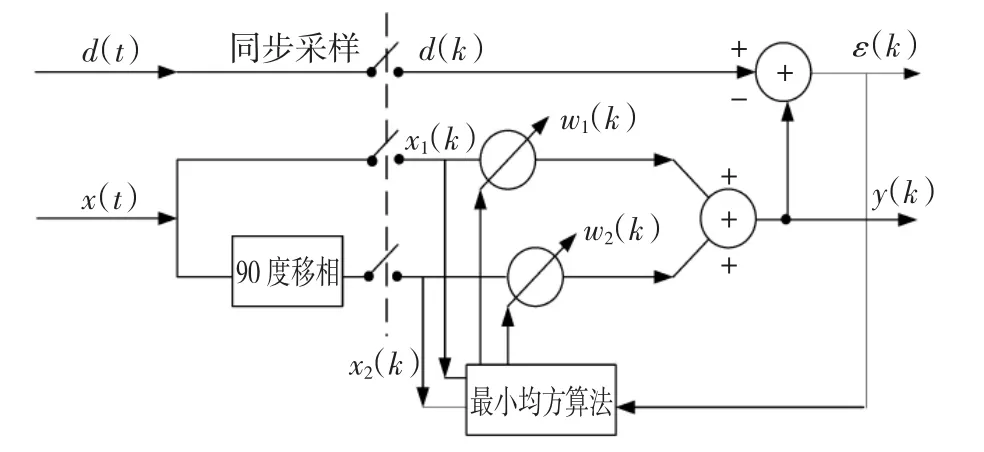
图1 自适应滤波器的原理Fig.1 The principle chart of the adaptive filter

由图1可知，误差为

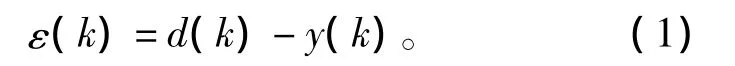
权的修正过程为

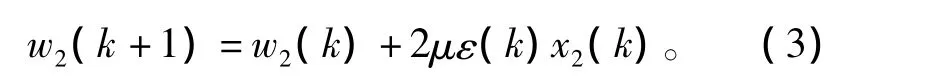
对于上述自适应滤波器，可以求得其闭环传递函数为

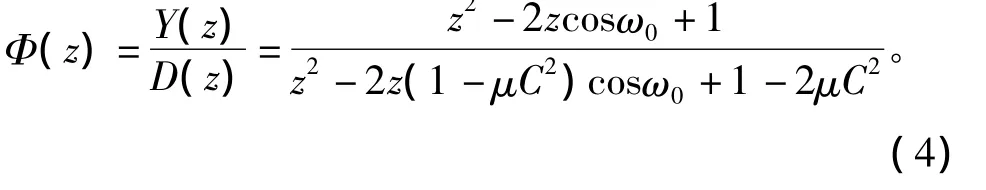
对于慢自适应过程而言，式(4)中μC2很小，这时闭环系统的极点为

由于通常μC2很小，所以极点在单位圆内，系统是稳定的。

上述自适应滤波器的带宽为

可见，自适应滤波器的带宽BW与步长μ成正比。因此，步长μ越小，越有利于克服频率为ω0信号的影响［1，4－5］。

为了兼顾自适应滤波器的收敛速度和滤波效果，自适应滤波器通常采用变步长取代固定步长。此时，权的修正过程为

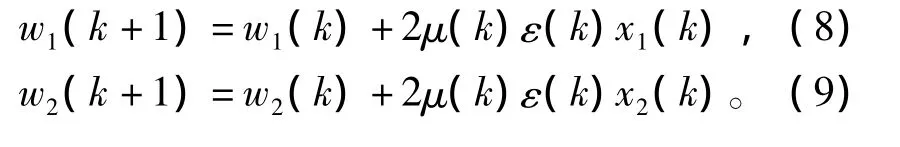
2 常见的变步长算法

本文称之为变步长算法1。

文献［3］提出的步长变化算法为

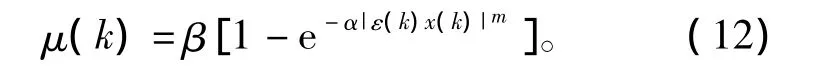
本文称之为变步长算法2。式(11)和(12)中，α、β、m均为待定的正数。实验证明，当取α=50，β=0.3，m=1时，可以取得较好的效果。可以看出，变步长算法1、2中，μ(k)与ε(k)或x(k)成一种非线性关系，这将增加算法的复杂度，不利于实时运算。

为了便于比较不同算法的滤波效果，模拟笼型异步电动机的断条故障信号的特点构造信号为

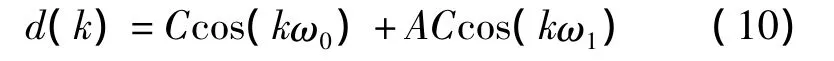
式中:ω0=100π rad/s;ω1=96π rad/s;A 为断条故障特征分量的幅值，通常情况下A=0～0.05，这里取A=0.02。同时，为了分析方便取C=1。文献［2］提出的步长变化算法为

3 新型的变步长算法

针对自适应调节过程ε(k)或x(k)是交变的特点，提出了一种新型的变步长算法，其表达式为

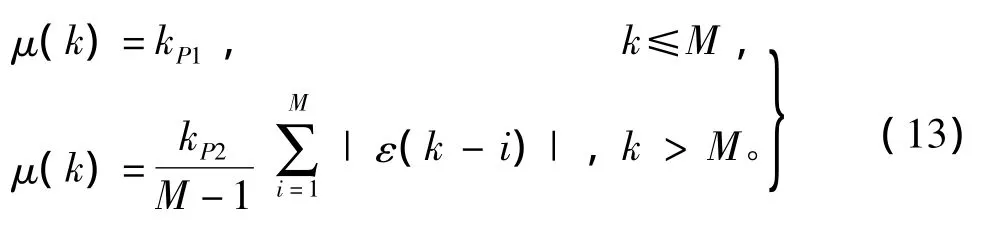
本文称之为变步长算法3。式中:kP1、kP2均为待定的正数;M为正整数。因此，kP1、kP2的选取应满足以下要求:根据初始误差|ε(k)|值的大小来选择kP1、kP2值，使得初始误差|ε(k)|在满足算法收敛的条件下所对应的μ(k)值尽可能大些，起到加快收敛的作用。这里，根据信号d(k)的特点和实验效果，取kP1=0.15，kP2=0.1，M=10。变步长算法 1、2、3 对应的步长变化情况分别如图2(a)、图2(b)、图2(c)所示。可以看出，当采用变步长算法1、2时步长μ(k)有较大的波动，而当采用变步长算法3时步长μ(k)基本上没有波动，这对缩短自适应调节时间是有利的。

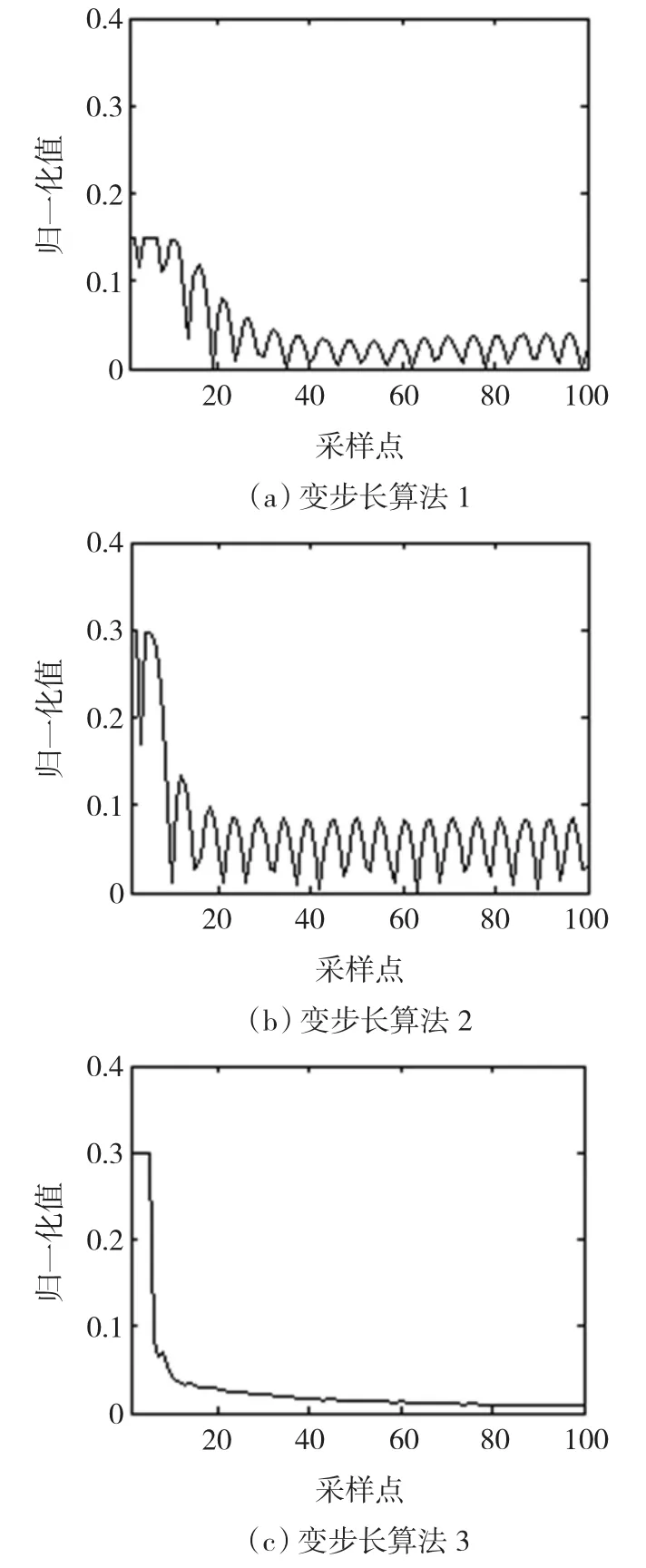
图2 步长变化过程Fig.2 The change process of the step size

针对式(10)所示信号，采用3种变步长算法处理后，再进行FFT分析的结果如图3(a)、图3(b)、图3(c)所示。其具体数值如表1所示。表中，ri为分量ω1与分量ω0的幅值谱密度值之比，这里i=1，2，r1、r2分别为采用自适应滤波器处理前、后的比值。自适应陷波之前，3种变步长算法所用信号相同，所以r1的值相同。经分析r1=0.066。

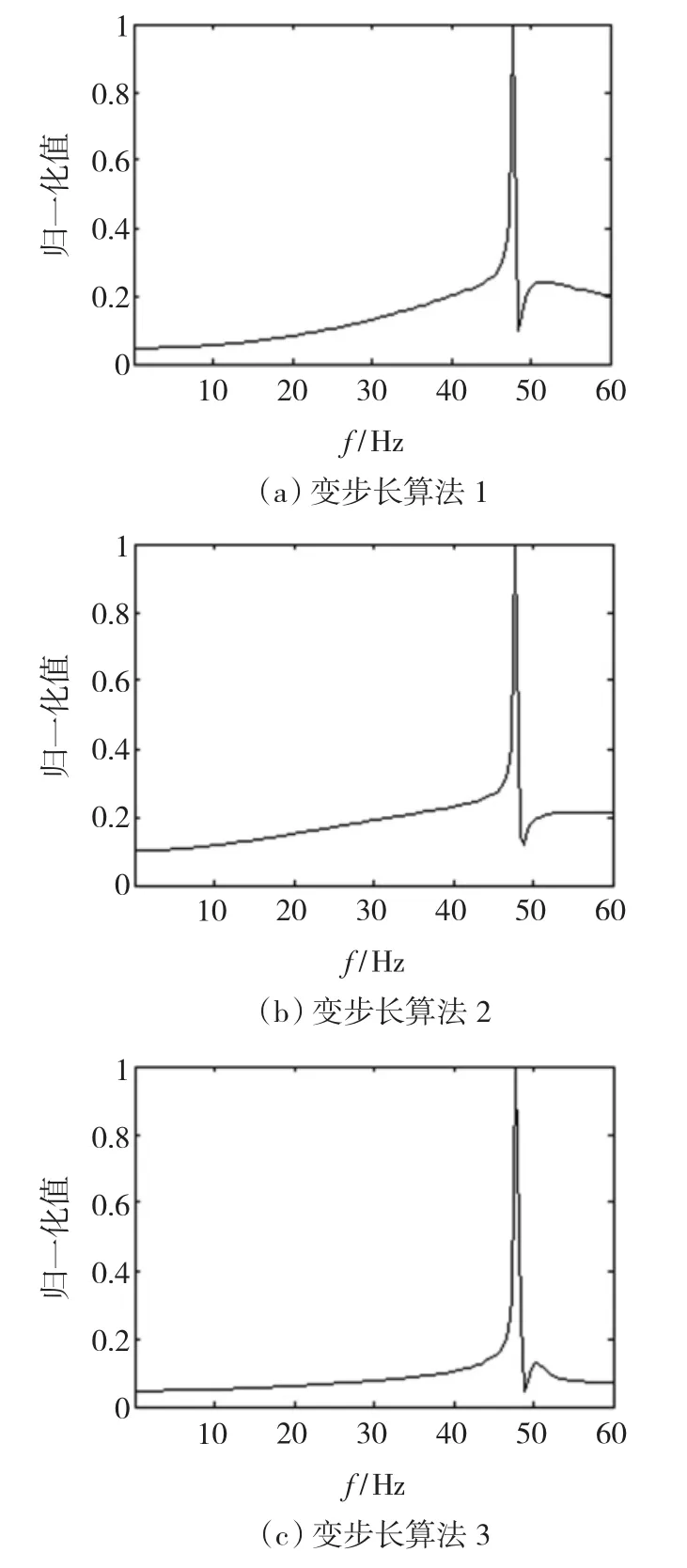
图3 滤波后FFT分析结果Fig.3 The analysis results of FFT after filtering

表1 3种变步长算法的效果Table 1 Effects of three variable step size algorithms

可以看出，变步长算法3的r2值最大，所以采用变步长算法3时对分量ω0的陷波效果比采用变步长算法1和2时的陷波效果要好许多。

4 新型变步长算法的应用

4.1 电动机断条故障诊断的原理

转子断条是笼型异步电动机常见的故障之一。正常时电动机定子电流仅含有电源频率f0=50Hz。但是，当转子出现断条故障时，定子电流中还会出现一个频率为f1=(1－2s)f0的故障特征分量，其中转差率为同步转速，n为电机转速。当转速n接近n0时，转差率s非常小，接近0，这时f1与f0十分接近。由于分量f1相对于基频f0非常小，所以若直接进行频谱分析，则分量f1会被基频f0所淹没，无法得到分量f1。目前，常用的方法是先采用自适应滤波器对定子电流进行处理，尽可能地减少分量f0，然后再通过频谱分析，判断定子电流中是否存在分量 f1，最后进行断条故障诊断［6－10］。这样，可以提高断条故障诊断的准确率。

4.2 电动机断条故障诊断的实例

实验中采用的笼型异步电动机的型号为TYPE100 －4，额定转速 n1=1 430 r·min－1，极对数p=2，电源频率 f0=50Hz，采样频率 fs=500Hz，采样点个数为N=1 024。典型工作状态如表2所示，r3为实际信号的电动机断条特征分量f1的幅值谱密度值d1与基频f0的幅值谱密度值d0之比。可以看出，在工作状态1下电动机转速较高，断条特征分量f1与基频f0较接近。在工作状态1、2下，针对采集的实际定子电流信号，采用三种变步长算法进行自适应滤波器处理后，再进行FFT分析的结果分别如图 4(a)、4(b)、4(c)和图 5(a)、5(b)、5(c)所示。其具体数值如表3所示，其中d1、d0仍分别为分量f1、f0的幅值谱密度值，r4为分量f1与分量f0的幅值谱密度值之比。

表2 滤波前的实验结果Table 2 Test results before filtering

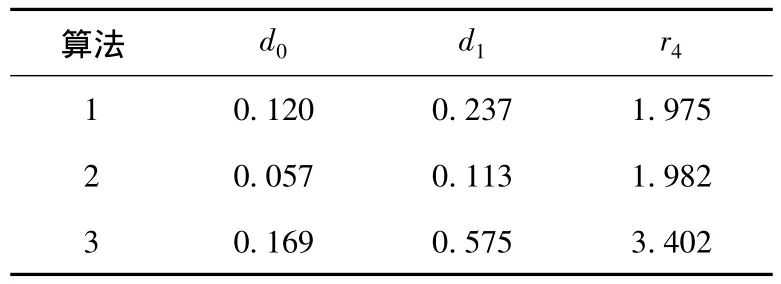
表3 状态1下滤波后的实验结果Table 3 Test results after filtering in the state 1

从表3和表4可以看出，在两种状态下新型变步长算法的r4比变步长算法1、2的r4大许多。尤其是采用新型变步长算法时，分量f1的幅值谱密度值较大，而且在许多情况下，例如工作状态2所示，分量f1的幅值谱密度值为最大值，这将有利于断条故障特征的提取。实验证明，新型变步长算法具有较好的处理效果。

表4 状态2下滤波后的实验结果Table 4 Test results after filtering in the state 2

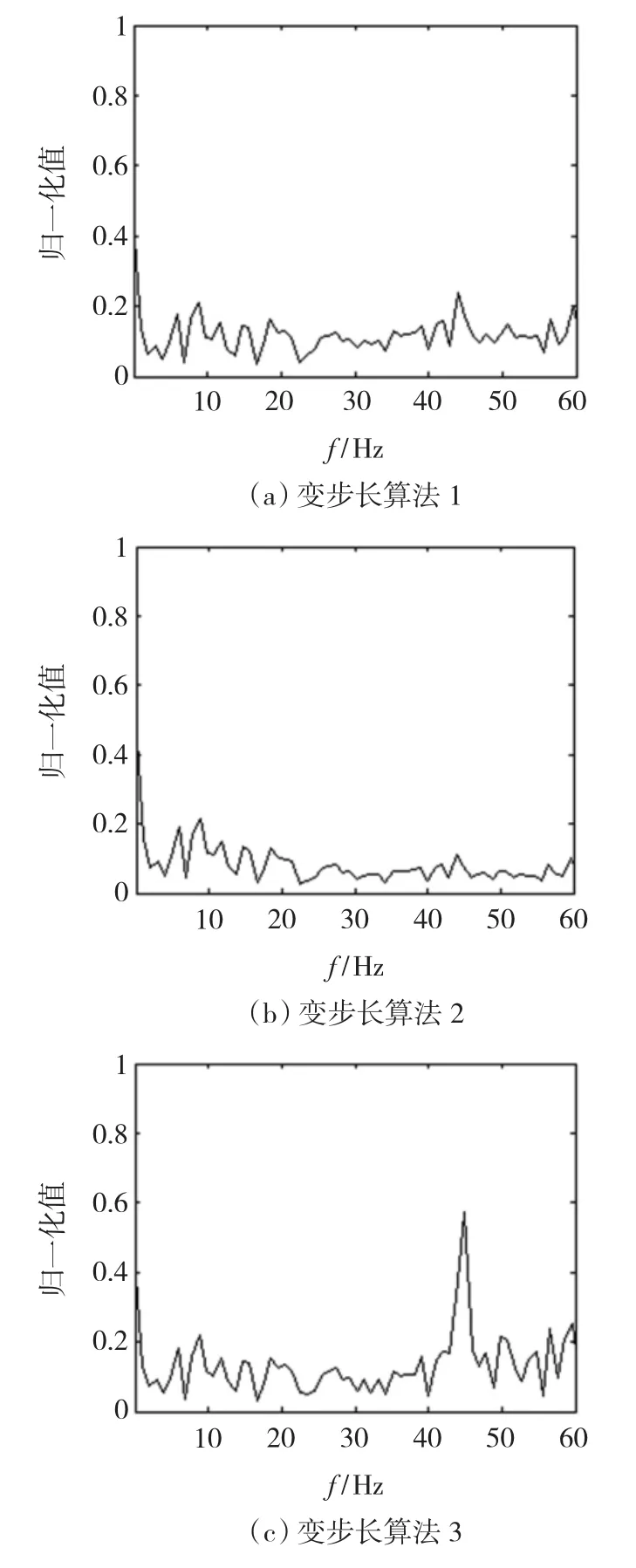
图4 状态1下滤波后FFT分析结果Fig.4 The analysis results of FFT after filtering in the state 1

从表1～表4和图3～图5还可以看出，在实际情况下，工作状态1、2下断条特征分量f1与基频f0的间隔分别为4.7Hz、14Hz，相对前面所述的仿真信号特征分量f1与基频f0的间隔2Hz要大许多，并且r3也比r1大一些。但是，r4与r2相比却小许多，其主要原因是仿真信号只含特征分量f1和基频f0，是理想信号，而实际信号含有一定的干扰信号，谐波成分较丰富，这对自适应滤波有一定的影响。总体看来，采用新型变步长算法提取实际信号的断条特征分量的效果是比较满意的。这里仅给出了两种典型状态的数据，在其他状态下也会得出同样的结论。

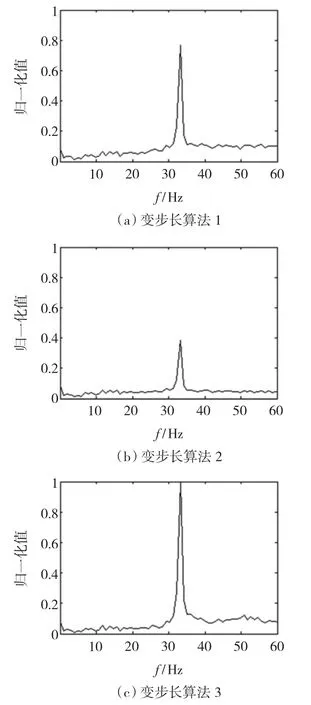
图5 状态2下滤波后FFT分析结果Fig.5 The analysis results of FFT after filtering in the state 2

5 结语

实验证明，新型变步长算法充分考虑了自适应滤波器调节过程中信号ε(k)或x(k)的特点，可以克服ε(k)或x(k)交变的影响，缩短自适应滤波器的调节时间。同时，新型变步长算法为线性算法，算法运算简单，有利于实时计算，为在线信号处理提供了方便。新型变步长算法不仅可以用于电动机断条故障诊断，而且可以推广应用于其他信号处理。

［1］ 吴斌，赵学增，滕志军.基于自适应陷波器的工频电力通信信号检测［J］.电力系统自动化，2003，27(20):35－39.

WU Bin，ZHAO Xuezeng，TENG Zhijun.Detection of power frequency communication signal based on adaptive notch filter［J］.Automation of Electric Power Systems，2003，27(20):35 －39.

［2］ 罗小东，贾振红，王强.一种新的变步长LMS自适应滤波算法［J］.电子学报，2006，34(6):1123 －1126.

LUO Xiaodong，JIA Zhenghong，WANG Qiang.A new variable step size LMS adaptive filtering algorithm［J］.Acta Electronica Sinica，2006，34(6):1123 －1126.

［3］ 覃景繁，欧阳景正.一种新的变步长自适应滤波算法［J］.数据采集与处理，1997，12(3):171 －194.

QIN Jingfan，OUYANG Jingzheng.A novel variable step size LMS adaptive filtering algorithm based on Sigmoid function［J］.Journal of Data Acquisition ＆ Processing，1997，12(3):171 －194.

［4］ 高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29(8):1094 －1097.

GAO Ying，XIE Shengli.A variable step size LMS adaptive filtering algorithm and its analysis［J］.Acta Electronica Sinica，2001，29(8):1094－1097.

［5］ WANG Xin，ZHANG Dongxia.Optimization method of fault feature extraction of broken rotor bar in squirrel cage induction motors［C］//Proceedings of the 2010 IEEE International Conference on Information and Automation，June 20 － 23，2010，Harbin，China.2010:1622－1625.

［6］ 罗铭，刘振兴，黄菲.变频电源笼型异步电机断条故障诊断仿真［J］.电机与控制学报，2008，12(2):139－142.

LUO Ming，LIU Zhenxing，HUANG Fei.Diagnosis simulation of broken rotor bars in squirrel cage induction motor fed with variable frequency power［J］.Electric Machines and Control，2008，12(2):139－142.

［7］ 许伯强，李和明，孙丽玲，等.小波分析应用于笼型异步电动机转子断条在线检测初探［J］.中国电机工程学报，2001，21(11):24－28.

XU Boqiang，LI Heming，SUN Liling，et al.The application of wavelet analysis to detect rotor bar breaking fault of squirrel cage asynchronous motor on-line［J］.Proceedings of the CSEE，2001，21(11):24－28.

［8］ 马宏忠，姚华阳，黎华敏.基于Hilbert模量频谱分析的异步电机转子断条故障研究［J］.电机与控制学报，2009，13(3):371－376.

MA Hongzhong，YAO Huayang，LI Huamin.Study on rotor brokenbar fault in induction motors based on spectrum analysis of Hibert modulus［J］.Electric Machines and Control，2009，13(3):371 －376.

［9］ 安永红，夏昌浩.笼型异步电动机转子断条故障诊断技术［J］.电力学报，2006，21(3):310－311.

AN Yonghong，XIA Changhao.Techniques of broken rotor bar fault diagnosis for squirrel cage induction motor［J］.Journal of E-lectric Power，2006，21(3):310 －311.

［10］ 王榕生，吴汉光，黄灿水，等.多断条笼型转子感应电动机导条电流分布［J］.电机与控制学报，2010，14(4):59－65.

WANG Rongsheng，WU Hanguang，HUANG Canshui，et al.Distribution of bar current on squirrel cage induction motor with multi-broken rotor bars［J］.Electric Machines and Control，2010，14(4):59 －65.

(编辑:刘素菊)

Novel variable step size algorithm of adaptive filter and its application

WANG Xin
(School of Electrical Engineering and Automation，Henan Polytechnic University，Jiaozuo 454003，China)

The variable step size algorithm affects the performance of the adaptive filter heavily.The step size of the usual variable step size algorithms has a certain relation with the error signal and the input signal.In the adaptive regulation process，the step size has a big fluctuation.This property severely affects the filtering effect of the adaptive filter.To solve these problems，a novel variable step size algorithm(NVSSA)was put forward by analyzing and comparing the usual variable step size algorithms.In the NVSSA，the absolute value of error signal was taken，and then its mean was found.The mean decided the change of the step size.The NVSSA can overcome the shortage of the step size fluctuation.The adaptive filter based on the NVSSA has a faster convergence rate and a less mean square error.In the end，the adaptive filter based on the NVSSA was used in the fault diagnosis of the broken rotor bar of the squirrel cage induction motor.Experiments show that the NVSSA can highlight the feature of the broken rotor bar fault and is propitious to the signal feature exaction.

adaptive filter;variable step size algorithm;broken rotor bar;fault detection

TN 911.72

A

1007－449X(2011)04－0023－05

2010－07－22

河南省高校科技创新人才支持计划项目(2008HASTIT022);河南省重点科技攻关项目(072102240006);河南省控制工程重点学科开放实验室开发基金项目(KG2009－10)。

王 新(1967—)，男，博士，教授，研究方向为故障诊断、信号处理和电气传动。