基于BP神经网络的脉冲涡流无损检测分析

王俊英，冯华勇

（四川工程职业技术学院，德阳 618000）

0 引言

脉冲涡流检测近年获得较大发展。与其他检测技术相比它具有检测灵敏度高、设备简单、操作方便、容易实现自动化的特点。脉冲涡流检测中涡流的影响因素有很多如缺陷的性质、形状、深度、被检测材料含杂质情况、被检测材料的磁导率、电导率等等，其中含有复杂的非线性变量关系。近年很多国家将神经网络技术用于解决涡流检测信号特征的识别上，这将使涡流检测技术在核工业、航空航天业中发挥重大的作用。

1 神经网络反向传播算法（back propagation，简称BP算法）

1.1 BP网络基本结构

人工神经网络是指模拟人脑神经系统的结构和功能，运用大量的处理部件，由人工方式构造的网络系统。神经网络理论是一个非线性动力学系统，并以分布式存储和并行协同处理为特色。它能较好的适应环境、总结规律和完成某种运算。人工神经网络是一个具有学习能力的系统。通常具有两种学习方式：有监督学习和无监督学习。前者可利用给定的学习样本学习模仿，后者则随输入信号的情况可自动发现输入信号的特征。

1.2 BP网络的学习算法

要使神经网络产生所希望的行为，必须对其进行训练，即网络学习。学习时每条连接都在不断的调整自己的权值，以使神经网络的输出和期望输出之间的误差达到最小，学习的效果直接影响到网络的预测精度。

BP算法的学习过程由正向传播和反向传播两部分组成，可分为四个过程：l）输入模式由输入层向输出层的模式顺传播；2）误差信号由输出层向输入层的误差逆传播；3）正向传播和逆向传播反复交替进行的网络记忆训练过程； 4）趋向收敛的学习过程。BP算法的学习流程如图1所示。

BP算法有三种数值优化方法为最速下降法、共轭梯度法（Conjugate Gradient Bakpropagation,CGBP）和牛顿法。其中，最速下降算法是最简单的算法，但收敛速度慢。牛顿法最快需要计算赫森矩阵和它的逆，计算量大。共轭梯度法是二者的折中：它不需要计算二次导数，但仍然具有二次收敛的特性（即有限次叠代后能收敛与二次函数的极小点）。因此采用了CGBP完成网络训练。

2 脉冲涡流无损检测中神经网络结构设计

2.1 网络数据的准备以及输入、输出层的设计

在设计网络之前，必须整理好训练网络的数据。本文为实现脉冲涡流表面裂纹深度的自动识别，将采用从原始数据中提取的反映表面裂纹深度的特征值作为输入。

本文实验分别采用了铜、铝、铁、不锈钢四种金属试件。如图2所示的试验数据是经过小波除噪处理之后的信号。

从图2中可以看出涡流峰值随着裂纹深度的增加而增大，与裂纹深度有着强烈的联系，完全可以表征裂纹深度。

因此本文将以脉冲涡流检测信号的最显著特征值即涡流峰值作为输入。本文训练集数据如表1所示。

输出量实际上就是网络训练后提供的期望输出，输出最能代表系统要实现的功能目标。选择相对容易，多网络的精度和训练时间影响不大。因为要对表面裂纹深度进行定量的识别，因此文中选择表面裂纹的实际深度作为输出。

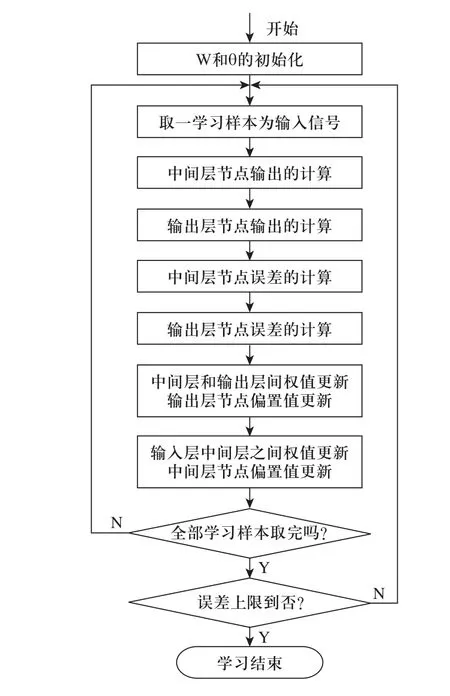
图1 BP算法流程图

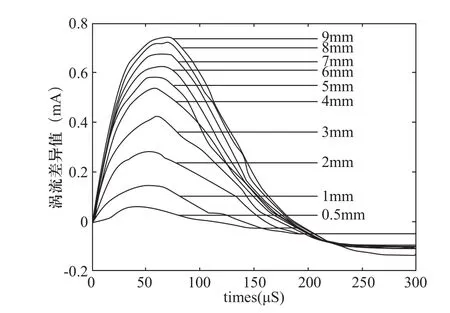
图2 铝试件试验结果

表1 BP神经网络训练样本集

2.2 传输函数以及隐含层数和隐含层节点数的确定

由于本网络的输入为涡流峰值，输出为表面裂纹深度，再根据传输函数的性质，本文的隐层传输函数选择常见logsig函数即可满足要求；而因为该神经网络输出为非－1和1之间的数值，故输出层激励函数选择线性函数，从而可以输出表面裂纹深度。

目前对隐含层数和隐含层节点数的确定还没有通用规则，但经过大量的实践有几点结论：对任何实际问题首先只用一个隐含层，使用较少隐含层节点数，然后不断增加隐含层节点数，直到获得满意性能为止，否则再使用两个隐含层。本实验隐含层的确定：由于当各节点均采用S型函数时，一个隐含层就足以实现任意判决分类问题。

理论研究已经证明，一个输入层、一个输出层、一个隐层的3层BP网络就可以逼近任何函数[8]。一般而言，增加隐含层数会增加网络的处理能力，同时也会使训练复杂化，并使训练样本数目和训练时间增加。所以本课题选择单隐层结构就完全能够满足需要。

隐含层节点数的确定：建立多层神经网络模型采用适当隐含层节点数是很重要的，往往是网络成败的关键。隐含层接点数太少，网络所获得的解决问题的信息太少，网络难以处理复杂的问题；隐含层接点数太多，网络训练时间急剧增加，且容易是网络训练过度，网络过于处理复杂。

而且，一个网络要能被推广，它的可调参数应当与训练集中的数据点数相当。在神经网络中，正如在所有建模问题中，要用足以表示训练集的最简单网络。只要有一个更小的网络能够工作就不要使用更大的网络，这就是所谓的剃刀原则。根据本实验训练集的输入、输出数据对数，根据经验，我们将隐含层节点数定为3至11个。根据以上所述采用试凑法对隐含层节点数进行确定。经过适当增减隐含层节点数反复试验比较网络的预测误差，发现隐层神经元个数目为6个时，网络的预测误差最小，故确定的隐层神经元个数目为6个。

3 表面裂纹深度的自动识别

CGBP神经网络的参数选择以下：学习速度初始值一般选择0.01到0.07之间，学习速度大，收敛速度快，反之则慢：若太大，则有可能修改过头，导致网络振荡、发散等。只有合理的学习速度才提高计算效率．这里值选为0.01，根据实际情况，训练精度为0.001。初始的偏置值和权值由

MATLAB初始化函数自行得到。然后利用表1所示的激励样本做为输入分别训练铝、铁、铜、不锈钢四种BP神经网络，训练成功后，利用另一组样本来判别该神经网络的识别能力，得到裂纹深度的估计值。

3.1 标准试件的拟合结果

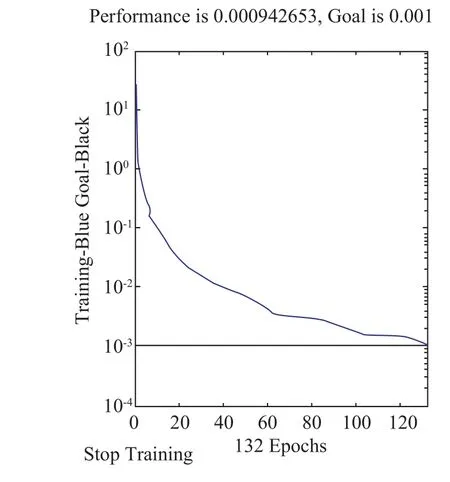
图3 AI训练集收敛图

使用裂纹深度从0.5mm到9mm等10个铝试件测量得到的涡流峰值作为训练集，而0.5mm到9mm等10个深度做为神经网络的目标集。经过若干次迭代后，该神经网络系统收敛于设计误差值。其收敛曲线如图3所示。

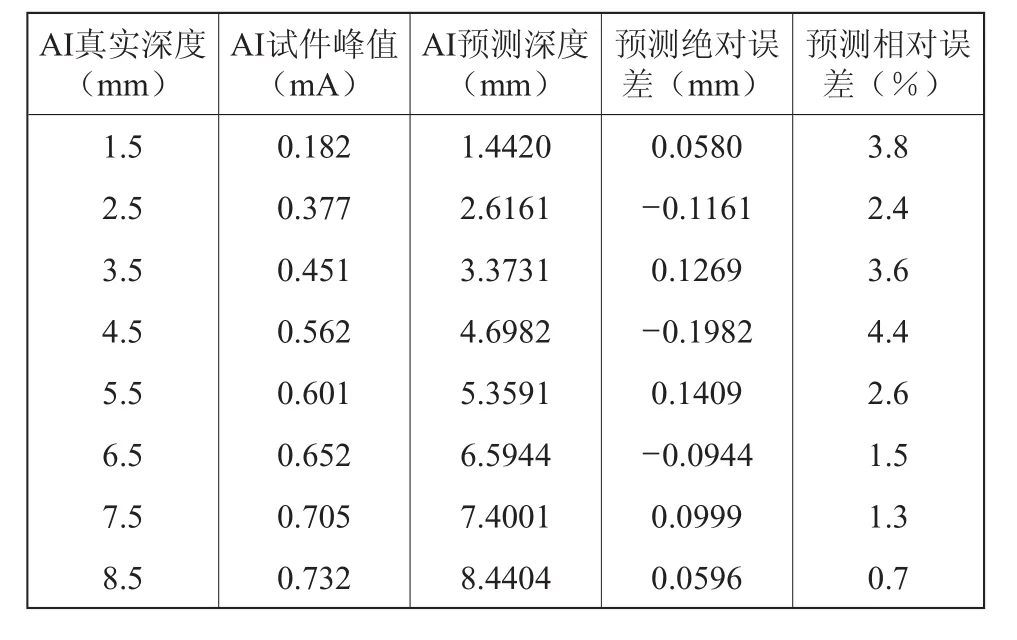
表2 Al测试集拟合结果

图4 AI测试集拟合图

试验结果显示训练成功后的BP神经网络有着良好的识别能力，能够较好地根据输入的AI试件的涡流峰值估计出其对应的裂纹深度。相对误差均在5%之内，而绝对误差值都在10-2mm数量级以下，具有较高的识别能力、较好的识别精度。说明应用BP神经网络对AI试件试验结果的拟合是成功的。达到了相应的识别精度。估计结果的拟合图如图4所示。

3.2 结果分析

试验结果显示训练成功后的CGBP神经网络有着良好的识别能力，能够较好地根据输入的不同材质试件的涡流峰值估计出其对应的裂纹深度。相对误差均在5%之内，而绝对误差值都在10-1mm数量级以下，具有较高的识别能力、较好的识别精度。说明应用BP神经网络对试验结果的拟合是成功的。但是，要想BP神经网络保持一定精度要求。就必须保持检测中的数据的稳定性并取得足够多的样本，这样才能利用神经网络来定量识别裂纹缺陷的深度值。

但是，由于神经网络方法是一种隐式的识别方法，其训练学习花费的时间比较多，学习的收敛速度比较慢，虽然从原理上讲，只要隐含层节点数，传递函数合适，收敛步数足够多，采用BP算法训练的神经网络可以任意精度逼近任意的非线性系统。但是在实际的网络训练过程中，由于BP算法中的搜索范围越大，局部极小点愈多，从而训练愈容易限入局部极小点问题的影响，此外，由于受到训练样本，计算机数值范围、非线性作用函数的选取等的影响，BP算法的收敛精度并不令人满意，有时甚至导致发散。尤其是涡流检测信号极易受到外界干扰，测得一个比较稳定的值比较困难的情况下，这种情况就更加容易发生。

[1] 孙晓云.智能型涡流无损检测系统的开发与信号处理的研究[D]. 西安: 西安交通大学, 2000: 3-26.

[2] 闻新. MATLAB神经网络应用设计[M]. 北京: 机械工业出版社, 2000: 214-296.

[3] 叶子郁. 脉冲涡流检测系统研究[D]. 四川: 西南科技大学, 2005: 1-28.

[4] 王素菊. 神经网络在涡流无损检测中的应用[J]. 南京航空航天大学学报, 1995, 27(5): 697-701.

[5] 幸玲玲, 王东进. 涡流检测中的组合神经网络模型[J]. 电子学报, 2002, 30(5): 734-737.

[6] B.Lebrun, Y.Jayet. Pulsed eddy current applications to the detection of deep cracks[J]. Material Evaluation, 1995, 53:1296-1300.

[7] 孙晓云等. 智能型涡流无损检测仪的研制[J]. 无损检测,2003, 25(9): 451-455.

[8] Martin T. Hagan. Neural Network design[M], China Machine Press 2002: 1-257.