淘汰赛编排算法理论研究
雷宾宾,董东风
(长沙通信职业技术学院,湖南长沙 410015)
在运动竞赛方法中,淘汰赛方法在很多体育项目的各级各类竞赛中被广泛运用。不管是采用手工编排还是计算机编排,我们都能完成淘汰赛的编排任务。然而,我们发现,在很多运动竞赛方法的相关教材、手册中,对于淘汰赛方法的论述却很不完善,导致实际编排结果有多“版本”现象。主要表现在以下两个方面的问题:
一是查表法问题:淘汰赛种子及轮空位置的编排都是采用查表法(计算数学平方根,一定要带着表格),给出种子位置表及轮空位置表,有些提供的表格数据还不全,甚至出现多个“版本”。至于表是怎么得来的,都描述不清楚,只是给出建立在手工编排基础上的“跟种子”原理理论,并没有给出计算方法。采用这种理论教学让学生很难掌握,以至于在实际手工编排运用中,特别是在无表对照的情况下,编排结果有多“版本”现象。
二是框图法问题:淘汰赛轮次编排通常都是采用手工画轮次框图的直观办法(参见图1单淘汰赛比赛轮次表),在表示“进级”上都是假定某位胜出,没有进级队编码。如果只是像单淘汰赛那样连续地画下去,有无编码也无所谓,总是能找到进级队的位置。但是,如果是像双淘汰赛或附加赛,再采用连续性框图画法恐怕会很复杂也很难表示[1],所以采用分组画法,例如双淘汰赛就是采用分胜组和败组的画法,但是,当参赛队很多的时候,能画出框图还并不一定能找到进级队的位置(当然还有画错的),因为,这种“两级”分组还不够完善,没能完整解决编排算法问题。所以,我们在实践中可以找到多个“版本”的双淘汰赛框图。
当然,我们的比赛并没有因上述问题而无法举行。我们只是想通过对淘汰赛方法的描述,让大家对该方法有一个完整的了解,使我们以后的淘汰赛编排更加规范,减少错误,避“黑编”之嫌。同时,为计算机编排提供算法理论,提高计算机编排的自动化程度。也可以为淘汰法的分类提供依据。
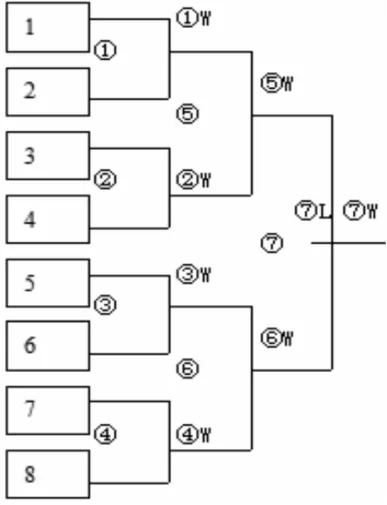
图1 单淘汰赛比赛轮次表
1 单淘汰赛编排方法
要进行淘汰赛轮次编排需要的第一个参数就是参赛队(人)数,参赛队数与位置数满足关系式:2n≥N(N表示参赛队数;2n表示位置数;n表示比赛轮次数=1,2,3,...),也就是说,淘汰赛的位置数必须是2的幂次方,比赛场次为(2n-1)-(2n-N)=N-1(参见图1)。如果是参赛队数小于位置数,只允许在第一轮出现2n-N个空位,遇到空位的一方轮空,使以后各轮不再出现空位。当确定了参赛队数后,淘汰赛的位置数、比赛轮次数、比赛场次数以及赛程也都确定了。剩下的还需要确定第二个参数“种子号码”,这个参数实际要解决两个问题,第一个问题:如何把参赛队分配到位置当中去,以此确定参赛队的赛程,常见的办法有两种,第一种办法就是采用“跟种子原理”排位;第二种办法就是采用抽签定位(不在此讨论)。第二个问题:在参赛队数小于位置数时,要确定哪些位置是空位(2n-N个)。
我们可以先假定有2n个种子号码(因为最多只有2n个种子),与循环赛及积分编排赛不同,淘汰赛种子号码与位置号码不是依序相对应的。循环赛及积分编排赛1号位置就排1号种子,2号位置就排2号种子,依此类推。而淘汰赛却不是这样。但是,淘汰赛种子号码与轮空是相对应的,也就是说,1号种子编在哪个位置,其对手的位置将是第一个空位,2号种子编在哪个位置,其对手的位置将是第二个空位,依此类推。如果我们知道了2n个种子的位置编排,我们就找到了位置号码与种子号码的对应关系,同时,也就解决了轮空问题。如果说没有种子队,或者有种子队但不能区分种子序号大小,那就只有抽签定位,可以分种子签和非种子签。而空位的确定还是按照“假想”种子位置的对手位置来确定。那么,如何编排2n个种子的位置呢,这就是“跟种子原理”,其算法我们可以根据“淘汰赛种子位置表”推算如下(参见表1):
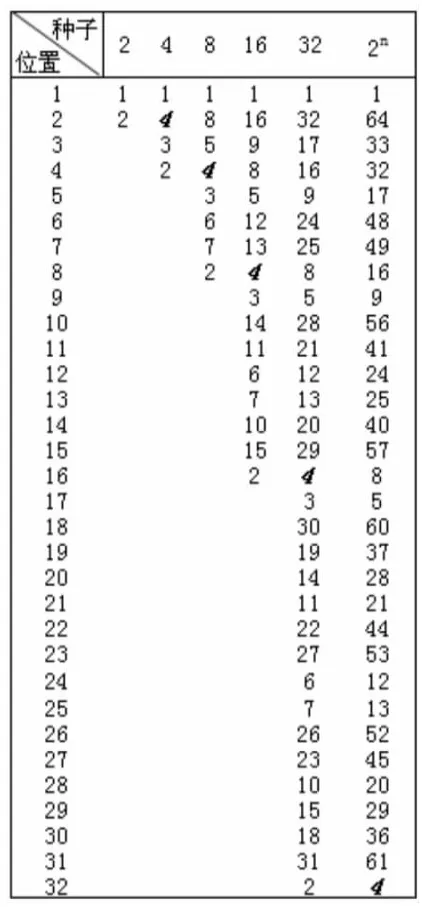
表1 淘汰赛种子位置表
当n=1时,只有21=2个位置,最多两个种子队,只能1号位置排1号种子(奇数),2号位置排2号种子(偶数)。我们以此确定为“根种子”(不是跟种子),因为,所有种子的位置编排都是从这两个种子推算而来。
当n=2时,22=4个位置,22上半区2个位置正好与21的2个位置奇偶相对应,即22上半区奇数位置上的种子号码等于21奇数位置上的种子号码“乘2减1”,这里为1×2-1=1;22上半区偶数位置上的种子号码等于21偶数位置上的种子号码乘2,这里为2×2=4。也就是“横向对应”,用21对应22上半区。22下半区2个位置正好与22上半区2个位置奇偶相对应。即22下半区奇数位置上的种子号码等于22上半区奇数位置上的种子号码加2,这里为1+2=3;22下半区偶数位置上的种子号码等于22上半区偶数位置上的种子号码减2,这里为4-2=2。也就是“纵向对应”,用22上半区对应22下半区。由此得到22的4个位置的种子编排为1432。
当n=3时,23=8。23上半区4个位置正好与22的4个位置奇偶相对应,即23上半区奇数位置上的种子号码等于22奇数位置上的种子号码“乘2减1”,这里为1×2-1=1和3×2-1=5;23上半区偶数位置上的种子号码等于22偶数位置上的种子号码乘2,这里为4×2=8和2×2=4。也就是“横向对应”,由此得到23上半区4个位置的种子编排为1854。23下半区4个位置正好与23上半区4个位置奇偶相对应,即23下半区奇数位置上的种子号码等于23上半区奇数位置上的种子号码加2,这里为1+2=3和5+2=7;23下半区偶数位置上的种子号码等于23上半区偶数位置上的种子号码减2,这里为8-2=6和4-2=2。也就是“纵向对应”,由此得到23下半区4个位置的种子编排为3672。合起来就得到23全区8个位置的种子编排为18543672。
以此类推,可以得到给定2n个种子的位置编排:
2n+1上半区奇数位置上的种子号码=2n奇数位置上的种子号码×2-1;
2n+1上半区偶数位置上的种子号码=2n偶数位置上的种子号码×2(横向)。
2n下半区奇数位置上的种子号码=2n上半区奇数位置上的种子号码+2;
2n下半区偶数位置上的种子号码=2n上半区偶数位置上的种子号码-2(纵向)。
这个算法的特点:每次推算都必须从“根种子”开始;奇偶对应,都与2有关;先横向对应,上半区用乘法;再纵向对应,下半区用加减法。
空位的确定其实就是依据种子号码的大小来优先确定的。比如有8个位置的淘汰赛,当只能确定一个种子时,依据“根种子原理”,这个种子排在1号位置;能确定两个种子时,第2号种子就排在8号位置。那么,当只有7队参赛时,2号位置就为空位;当只有6队参赛时,第二个空位就是7号位置。换句话说,可以把空位置可以看作是大于参赛队数的种子号码,这样,如果某位置上依据根种子原理排位的种子号码大于参赛队数,那么,就可判定该位置为空位。
对于多场淘汰赛来说,其编排实质就是单淘汰赛,只是在决定胜负的时候不是以一场来决定,而是要进行多场比赛,这就好比是一场比赛是由多“局”来决定胜负一样,如排球等项目。
2 交叉淘汰赛位置编排方法
所谓交叉淘汰赛,实际就是淘汰赛,只是在位置编排上采用交叉排位。例如,同组前四名交叉淘汰,1234位置号码对应的前四名(种子号码)是1423;又如,两组前两名交叉淘汰,1234位置号码对应的两组前两名(种子号码)1A2B2A1B。胜队争冠亚军,负队争三四名。
假设我们把分组看成是有序的(我们在循环赛种子分组时就有采用按组序蛇形分组),我们按“名次”+“组序”组合排序,可以得到象1A、1B、2A、2B这样的序列,我们可以把这个序列看成是种子序列1234,然后,我们采用根种子位置编排方法来排位,可以看到,排位的结果与交叉排位是相同的。这就证明交叉排位实际就是遵循着“跟种子原理”。
3 单淘汰附加赛
单淘汰赛只能判别前两名。在单淘汰赛失败的队,可以有附加赛,以判别所有队名次。由于没有附加赛计算方法,所以,我们可以把单淘汰赛附加赛分解成多个单淘汰赛组,而每个单淘汰赛组我们都有计算方法,这样,我们就能计算单淘汰附加赛了。
按单淘汰赛失败轮次进行分组,把每轮淘汰的队数再组成单淘汰赛组,直到只淘汰一个队时不再分组,单淘汰赛有n轮就分n-1组,在n-1组中,每个组又按轮次淘汰分组,依此类推,共可分2n/2个组。每个组的组别就是“名次修正值”,名次修正值=淘汰时所在组的名次修正值+淘汰时该轮所淘汰的队数,每个组都有一个唯一的名次修正值(参见图2单淘汰附加赛比赛轮次表)。
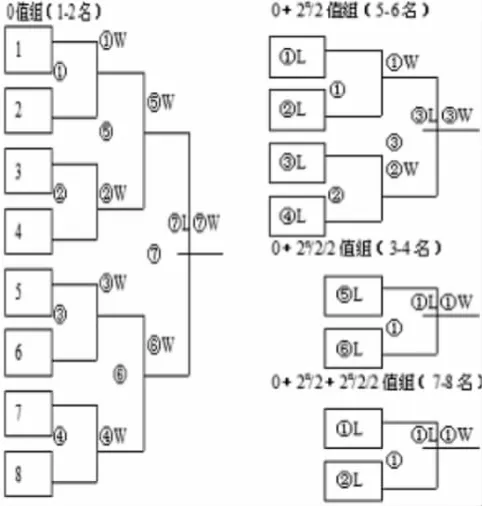
图2 单淘汰附加赛比赛轮次表
最初的单淘汰赛“本赛组”的名次修正值是0,说明该组单淘汰赛能够判别的前两名就是实际前两名;本赛组第一轮淘汰2n/2个队,名次修正值(组)就等于0+2n/2,说明该组单淘汰赛最后产生的前两名还需要加上0+2n/2修正值才是其实际名次;本赛组第二轮淘汰2n/2/2个队,名次修正值(组)就等于0+2n/2/2,说明该组单淘汰赛最后产生的前两名还需要加上0+2n/2/2修正值才是其实际名次。依此类推。
可以通过“组别+组场序”来唯一确定一场比赛,因为每个组的场序也是唯一的,那么,每场比赛胜负的队,胜队用W表示,负队用L表示,这样我们就可以用“组别+组场序+胜负”编码来唯一表示“进级队”。
4 双败淘汰赛编排方法
双败淘汰赛是为了给单淘汰赛失败的队增加一次机会,采用失败两场才被淘汰的比赛办法。对此,我们同样可以依照单淘汰附加赛的分组办法,采用按失败轮次进行分组,形成多个单淘汰赛组来寻求编排算法。不同的是,由于每个单淘汰赛组并不能产生最终名次,所以,对各个单淘汰赛组的第一名还需要编排比赛最终产生出可判别的名次。为此,我们把双败淘汰赛依次分成胜组、败组、梯级挑战组和决赛组(参见图3双败淘汰赛比赛轮次表)。
胜组就是单淘汰赛“本赛组”,所产生的第一名未输一场而直接进入决赛组。
败组是按胜组的轮次顺序进行分组,胜组每一轮淘汰的队组成一个单淘汰赛组。由于胜组最后一轮只淘汰一个队,所以直接成为该组第一,这样,败组实际只有n-1个单淘汰赛组,每个败组又进行单淘汰赛共产生n个败组第一,n个败组第一按在胜组淘汰时的轮次序号依次进入梯级挑战组的对应位置。
梯级挑战组的位置数正好是胜组轮次数,比赛轮次为n-1轮,每轮一场比赛,可判别的名次为n名。挑战顺序按位置序号是从第1位开始向第2位挑战,直到挑战第n位,因此,梯级挑战组第n-1轮产生的胜队为该组第一名进入决赛组。
决赛组只有两个队,一个是胜组第一,另一个是梯级挑战组第一。如果是梯级挑战组第一获胜,按以往理论要附加一场比赛。但是,从梯级挑战赛的角度来看,决赛组就是梯级挑战赛的最后一轮,所以没有必要附加一场比赛,且附加一场比赛只会带来组织上和预算上的困难。
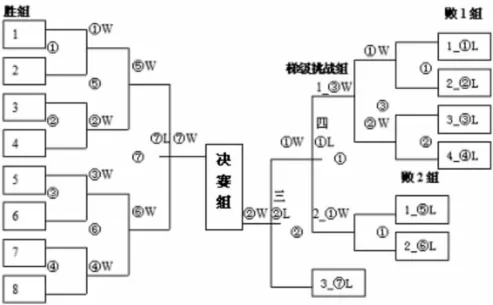
图3 双败淘汰赛比赛轮次表
双败淘汰赛方法是一种复合方法,其中包含单淘汰赛和梯级挑战赛两种方法。双败淘汰赛总轮次数为2n,即胜组轮次+梯级挑战组轮次+决赛组轮次。总场次数为2(N-1),即胜组场次+败组场次+梯级挑战组场次+决赛组场次。可判别名次为n+1名。在表示“进级队”时,同样可采用单淘汰附加赛的编码方法,即“组别+组场序+胜负”编码来唯一表示。
在上述对淘汰赛编排方法的描述中,我们主要提出了两个算法,一个是“根种子”位置编排算法;另一个是“分组编码”算法。通过这两个算法我们解决了以往“查表法”和“框图法”所存在的问题。当然,我们的水平有限,算法中难免存在一些问题,希望大家给予指出,我们将进一步加以改进。
[1]郭玉佩.篮球竞赛裁判手册[M].北京:人民体育出版社,1999.
[2]王蒲,等.淘汰制竞赛的“轮空”问题研究[J].中国体育科技,2000,36(1).
[3]许浒,等.对国际国内模糊状态下的编组与排号定位之探究[J].中国体育科技,2005,41(3).
[4]成登荣.完善双淘汰制的再探讨[J].北京体育大学学报,1999,22(4).
[5]方加艳.谈谈对双淘汰赛的认识[J].中国学校体育,1999,(3).
[6]赵伏生.乒乓球竞赛规则中关于淘汰赛种子号码位置计算方法的探讨[J].潍坊学院学报,2003,3(4).
[7]王斌.浅谈运动竞赛编排中的排位顺序[J].山西师大体育学院学报,2006,21(z1).
[8]吴飚.在体育竞赛编排中根种子原理的算法[J].长沙铁道学院学报(社会科学版),2006,7(4).
[9]董东风,等.双淘汰赛轮次编排研究[J].企业家天地,2008,(5).

