钢管自应力混凝土短柱长期荷载作用下变形性能研究
常 旭, 黄承逵
(1.河南理工大学土木工程学院,河南焦作 454000;2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024)
0 引 言
钢管自应力混凝土是利用自应力膨胀混凝土代替普通混凝土浇筑于钢管内而形成的一种新型结构.膨胀混凝土因膨胀受到钢管限制而在混凝土内产生一种化学预应力,与普通钢管混凝土结构相比,核心混凝土在承载之前就处于三向应力状态,有效约束了混凝土在承载中前期的横向变形并提高了构件的极限承载力[1、2].与普通钢管混凝土结构相比,钢管自应力混凝土构件中,核心混凝土受到的约束作用在承载之初就存在,约束效应要好于普通钢管混凝土结构,但同时也承受了轴向初应力,这样势必会造成徐变变形增大,对构件承载力造成不利影响.可见,钢管自应力混凝土构件徐变变形要更为复杂一些.
1 试验概况
本次试验采用的水泥为硫铝酸盐自应力水泥.钢管的屈服强度为341 MPa.部分试件的几何尺度等参数如表1所示.在钢管的中部轴向和环向分别对称贴了4个电阻应变片来测量钢管自应力混凝土的膨胀变形量,采用UCAM数据采集系统对试件进行了连续35 d的变形测量.本次试验共设计试件20根,其中10根施加长期荷载,另外10根为对比件,只进行一次性加载试验.

表1 试件一览表Tab.1 General view of tested specimens
本次试验采用如图1所示的加载装置,其由端板和拉杆组成,端板为250 mm×250 mm×30 mm的钢板,拉杆直径为40 mm.在试验前,先对钢拉杆力学性能进行标定.在长期持载过程中,主要通过让拉杆产生相同的变形来确保试件处于轴向受压状态.通过拧紧两端螺母的方式施加荷载,并通过荷载传感器控制,同时通过钢拉杆进行校核.持载一段时间后,钢管混凝土产生徐变变形,钢拉杆出现松弛现象,要进行不间断的补载.由于构件持载初期徐变变形较大,最初的两个月基本上2~3 d需要补载一次.两个月后基本上一周补载一次.需要指出的是在试验过程中,试件XZ1-3、XZ2-1上的应变片受到了损害,无法获得正确的数据;试件XZ3-2测得的数据比较分散,本文在后面的分析中,舍弃了该部分的数据.

图1 试件加载图Fig.1 Schematic of specimen loading
2 核心混凝土自应力计算
核心混凝土的膨胀作用可使得钢管中产生环向和轴向的拉力,如图2所示.由于采用的是薄钢管,可以认为环向应力沿管壁厚均匀分布;同时径向应力因为较小,可以忽略不计.根据实测钢管的轴向和环向变形,可由式(1)计算出钢管中产生的环向和轴向应力:

式中:σθ、σz分别为钢管中产生的环向与轴向应力;εθ、εz分别为试验测得的钢管外壁上环向和轴向应变;Es、μs分别是钢管的弹性模量及泊松比.
按图2(a)所示平衡条件2σθ·t=2rq,可得

式中:r为钢管内半径,t为钢管壁厚.根据轴向平衡条件As·σz=Ac·σcz,解得


图2 钢管受力示意图Fig.2 Stress of the steel tube
3 徐变计算
3.1 持载后核心混凝土的瞬时应力
对普通钢管混凝土而言,如果轴压比不大,可以认为施加长期荷载以后钢管和混凝土单独受力,两者按照各自的刚度分配荷载.对于钢管自应力混凝土构件而言,钢管和混凝土在承受荷载之前就产生相互作用,显然不能按照刚度来分配外荷载,本文参考文献[3],对持载后钢管自应力混凝土短柱截面的应力分布规律进行推导.
持载前,钢管和核心混凝土就相互作用且处于平衡状态,根据前文分析,可认为钢管处于平面应力状态,核心混凝土处于三向受压状态.假设施加长期荷载后,钢管和核心混凝土发生了瞬时变形,钢管的环向和轴向应力变化量分别为Δσs1、Δσs2,核心混凝土的轴向和径向应力变化量分别为Δσc1、Δp.由于在本次试验中,轴压比都基本在0.4左右,可以假定施加荷载后,钢管和混凝土均处于弹性状态,由胡克定律可知,在核心混凝土中:
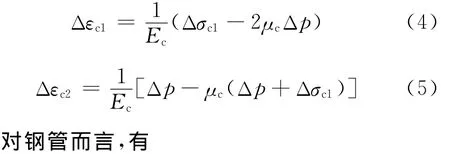

假设施加的长期荷载为N,那么有
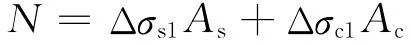
根据轴向和径向变形协调,有
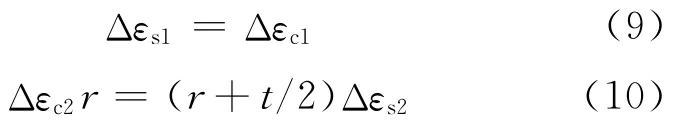
把式(4)~(7)分别代入变形协调条件(9)及(10),并消去Δp,可得
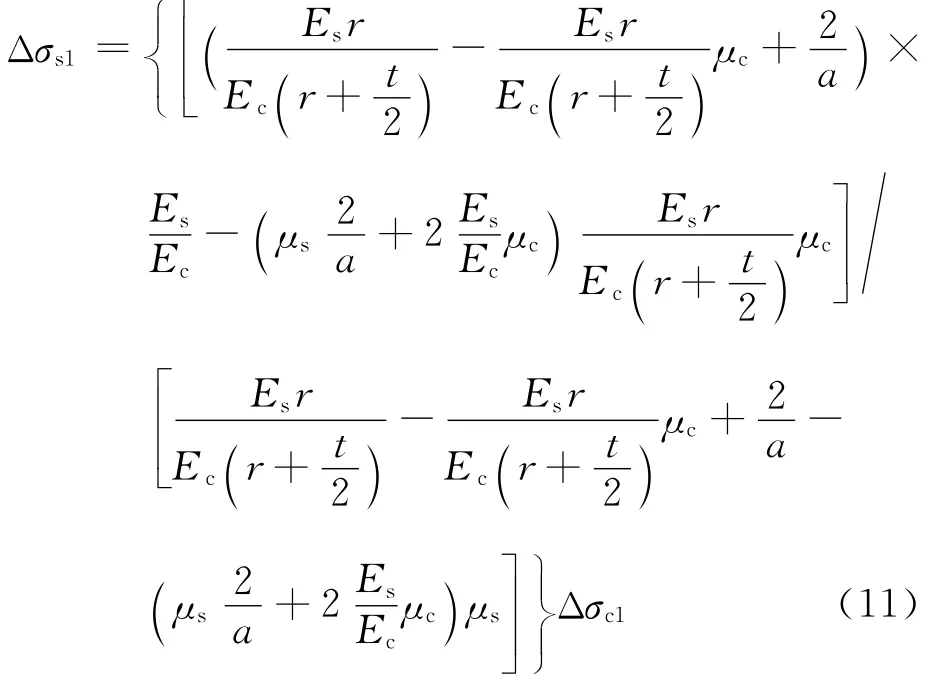
结合平衡条件N=Δσs1As+Δσc1Ac,可以得到持载后,核心混凝土上的瞬时应力变化量Δσc1及Δp.因此,核心混凝土上的瞬时应力可分别由下式表示:

3.2 徐变系数及计算方法的选取
徐变变形的计算主要有两个方面:徐变系数选取和计算方法的确定.本文的徐变系数采用ACI209委员会推荐的混凝土徐变系数:

其中max(t0)为徐变的最终值,具体计算参见文献[4].
关于混凝土徐变变形的计算理论比较多,本文采用龄期调整的有效模量法[4],徐变变形可表达为


χ(t,t0)为老化系数,按照文献[5]的统计结果,老化系数可以表示为
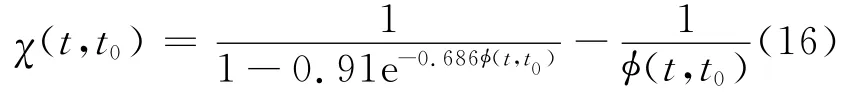
由前文分析可知,核心混凝土处于三向受压状态下,按照文献[6]的方法,可以采用“名义应力”来描述核心混凝土的实际受力大小.核心混凝土的轴向徐变可以表示为
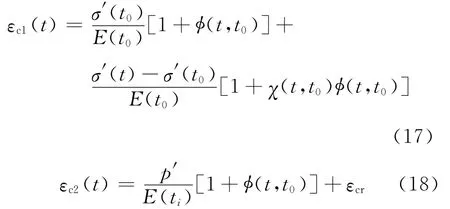
σ′为“名义轴向应力”,具体表达式为

p′为“名义径向应力”,可用下式表示:
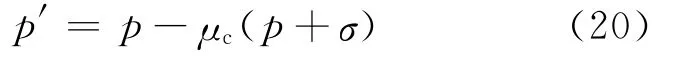
εcr是轴向徐变泊松比引起的变形,可以表示为εcr=μ′c[εc1(ti)-εc1(t0)].
这样就把采用龄期调整的有效模量法从一维推广到了三维,可以采用逐步计算的方法来求得徐变变形,具体的计算过程如下:
(1)在龄期t0给出所持荷载的大小,根据上述的计算公式,确定施加外荷载以后钢管和混凝土的实际应力大小.
(2)ti-1到ti时段内,核心混凝土上的应力变化量为Δσc1,根据ti-1时刻核心混凝土的径向应力,按照前述计算方法求得核心混凝土在ti-ti-1时间段内所发生的徐变变形量.根据轴向和径向变形协调条件:Δεc1=Δεs1及Δεc2r=Δεs2(r+t/2),可得钢管在轴向和环向所产生的应变,最后由胡克定律,可得钢管内的应力变化量.
(3)由求得的钢管内的应力及核心混凝土上的应力,判断是否满足力的平衡条件:Δσc1Ac=Δσs1As,如果不满足,需要返回(2)继续调整Δσc1,直到平衡条件得以满足.
(4)给定新的时间增量,重复步骤(2)、(3).
按照上述方法,对本次试验的试件进行了计算,试验结果和计算结果对比如图3所示,两者基本吻合,肯定了上述计算方法的可行性.

图3 徐变变形试验及计算结果对比Fig.3 Creep curves of tested and calculated results
3.3 参数分析
本节对影响钢管自应力混凝土构件徐变变形的主要因素,如加载龄期、含钢率、轴压比和核心混凝土的强度等级[6~8]及初始自应力等进行了分析计算.
轴压比对徐变变形的影响规律如图4所示.模型的参数为环向自应力p0=3 MPa,轴向自应力σc10=5 MPa,混凝土为C50,钢管为Q235钢,其内径和壁厚分别为50 mm和3.5 mm.从图4可知,钢管自应力混凝土轴压柱的徐变变形随着轴压比的增大而增大.
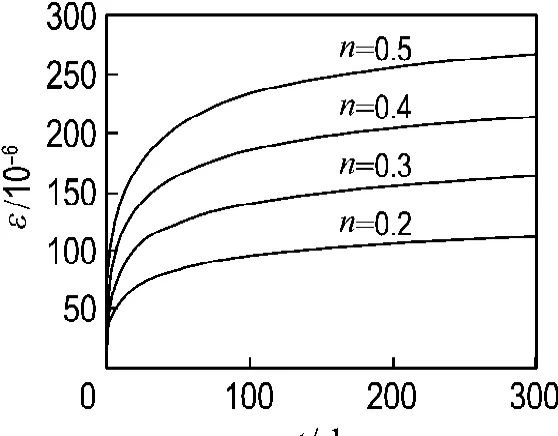
图4 应力级别对徐变曲线的影响规律Fig.4 Effect of axial load ratios on creep curves
图5表示加载龄期对钢管自应力混凝土轴压柱徐变变形的影响规律.采用的计算参数与上文所述一致,只不过轴压比为定值0.35;加载龄期为变量,其变化范围为7~90 d.
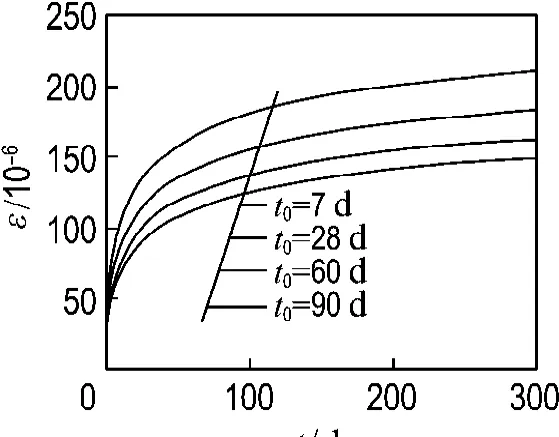
图5 加载龄期对徐变曲线的影响规律Fig.5 Effect of load age on creep curves
图6表明钢管自应力的徐变变形随着含钢率的增大而减小.主要是因为含钢率越大,钢管对核心混凝土提供的约束强度越高,限制构件轴向变形的发展;同时含钢率增大,能够更多地分担从核心混凝土卸载下来的荷载,从而保持较小的轴向变形.模型的计算参数为轴压比n=0.35;加载龄期28 d;含钢率从0.10逐步增加到0.37;其他参数不变.
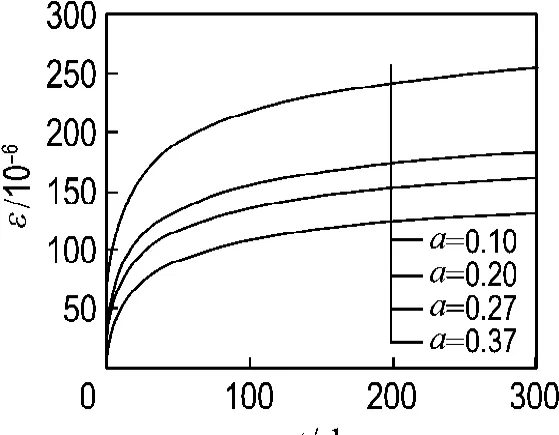
图6 不同含钢率对徐变曲线的影响Fig.6 Effect of steel ratio on creep curves
承载前,钢管和核心混凝土中存在相互作用的自应力,这是其重要的特点.图7(a)表明,钢管自应力混凝土的轴向变形是随着径向自应力的增大而减小的,可见环向自应力的存在有利于减小轴向徐变.模型的计算参数为轴压比n=0.35;加载龄期28 d;径向自应力的变化范围为0~8 MPa,轴向自应力为0,其他参数与上文采用的计算模型相同.然而钢管自应力混凝土结构中,不仅存在径向自应力,并且也存在轴向自应力.从图7(b)可知,如果考虑了轴向自应力的影响,钢管自应力混凝土的徐变变形要大于普通钢管混凝土同类构件.虽然环向自应力可有助于减小轴向徐变,但是由于其同时又要承受一定的轴向初应力,且轴向初应力引起的徐变也要大于环向自应力对徐变的有利影响,所以,钢管自应力混凝土的徐变变形随着自应力的增加而增大.根据试验获得的初始自应力的规律,图7(b)中,自应力参数分别为p=0,σc10=0;p=3 MPa,σc10=5 MPa,p=6 MPa,σc10=9 MPa.
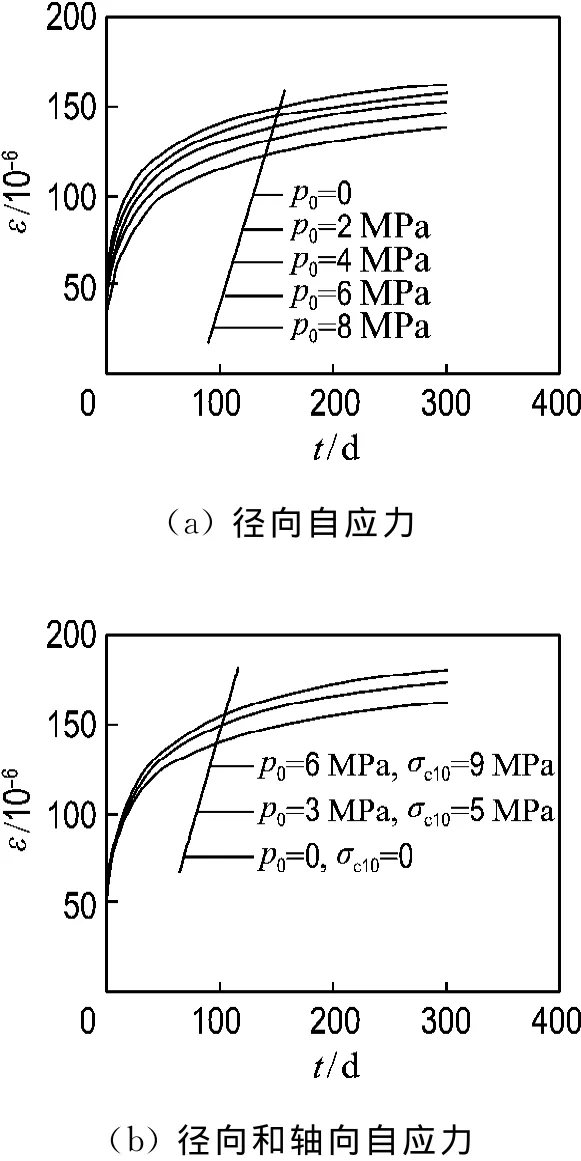
图7 自应力水平对徐变变形的影响Fig.7 Effect of self-stress on creep curves
4 结 论
(1)与普通钢管混凝土一样,轴压比、含钢率及加载龄期等对钢管自应力混凝土徐变变形有明显的影响;其变形规律与普通钢管混凝土基本一致.
(2)环向自应力对控制核心混凝土的轴向徐变变形有积极的意义,但实际的钢管混凝土结构中除了环向自应力外,还要承担轴向自应力,因此钢管自应力混凝土轴压柱的徐变要大于普通钢管混凝土轴压柱.
由于钢管自应力混凝土结构的受力状态比较复杂,本文的研究结果可为今后进一步研究该结构的性能提供参考.
[1]黄承逵,徐 磊.钢管自密实自应力混凝土轴压短柱力学性能研究[J].大连理工大学学报,2006,46(5):696-701
(HUANG Cheng-kui,XU Lei.Research on mechanical performance of self-compacting and selfstressing concrete-filled steel tube short column under axial loading[J].Journal of Dalian University of Technology,2006,46(5):696-701)
[2]徐 磊.钢管自应力免振混凝土轴压柱设计理论研究[D].大连:大连理工大学,2006
[3]王元丰,韩 冰.徐变对钢管混凝土轴心受压短柱禁锢应力影响分析[J].铁道学报,2000(S1):92-94
[4]周 履,陈永春.收缩徐变[M].北京:中国铁道出版社,1994
[5]顾建中,刘西拉.轴向载荷作用下钢管混凝土的徐变[J].中国公路学报,2001,14(4):59-62
[6]王元丰,韩 冰.钢管混凝土轴心受压构件徐变分析[J].中国公路学报,2000,13(2):57-60
[7]韩 冰,王元丰.钢管混凝土小偏心受压构件徐变分析[J].工程力学,2001,18(6):110-116
[8]韩林海,杨有福.长期荷载作用对矩形钢管混凝土轴心受压柱力学性能的影响研究[J].土木工程学报,2004,37(3):12-18

