超磁致伸缩薄膜悬臂梁静力学分析
王福吉, 刘 巍, 贾振元, 刘慧芳, 赵显嵩
(大连理工大学精密与特种加工教育部重点实验室,辽宁大连 116024)
0 引 言
超磁致伸缩薄膜(GMF)是一种新型的功能材料,具有能量密度高、响应速度快和可实现无缆驱动等优点,在MEMS系统微执行器、传感器以及其他功能元件中有着很好的应用前景.国内外科学家针对GMF进行了大量的研究工作,在其变形机理、有限元仿真和微执行器、传感器设计上取得了很多成果[1~6].
然而,目前仍然缺乏针对GMF的静力学特性和动力学特性的分析研究,而对GMF的静、动力学特性的准确分析是GMF微器件精确控制的基础,所以,薄膜的静、动力学特性研究对其进一步的应用研究有着非常重要的意义.
因此,本文选取福州大学采用磁控溅射方法制备的正负复合GMF悬臂梁作为研究对象,通过对其变形进行合理的简化建立简单实用的理论模型,继而对以铜、聚酰亚胺为基片的两种GMF悬臂梁进行静力学特性实验研究,以期为进一步研制开发GMF微型器件,推广GMF微型器件在工程中的应用奠定基础.
1 薄膜悬臂梁静力学分析
1.1 弹性刚度的求解
如图1所示,本文研究的GMF悬臂梁为双层悬臂梁,即在基片上下表面均溅射磁致伸缩材料.其中,基片上表面溅射正磁致伸缩材料(Tb0.27Dy0.73)43Fe57,下表面溅射负磁致伸缩材料Sm1.9Fe2.这种正负复合薄膜悬臂梁较单层GMF悬臂梁具有更大的磁致伸缩力,可使悬臂梁结构产生更大的弯曲变形.GMF悬臂梁由不导磁的塑料夹具固定在驱动磁场中.当施加沿薄膜悬臂梁长度方向的激励磁场时,正磁致伸缩材料因磁致伸缩效应沿磁化方向伸长,负磁致伸缩材料则缩短.这样,正负磁致伸缩材料层对基片形成了弯矩进而使其发生弯曲变形.

图1 GMF悬臂梁的结构Fig.1 GMF cantilever beam mechanism
磁致伸缩的本质是磁能和机械能之间的转换过程,弹性刚度是衡量材料机械能量转换能力的关键参数.项目研究的薄膜悬臂梁是由正负磁致伸缩材料溅射到基片上制备成的,3种材料各自的弹性常数都不同,因此在进行薄膜悬臂梁的静力学分析前,必须对其有效弹性刚度进行分析计算.
将项目研究的正负复合GMF悬臂梁视为由正、负磁致伸缩单层膜和基片组成的复合梁.假设这3种材料的最大应力均不超过其比例极限,采用当量宽度法求解其中性轴位置和等效抗弯刚度[7].这里以聚酰亚胺基片正负复合GMF悬臂梁为例说明当量截面法的求解过程,其结构如图2(a)所示,选用聚酰亚胺基片的弹性模量为当量模量,则正、负磁致伸缩薄膜的当量宽度分别为bTb、bSm,如图2(b)所示.根据应变与应力关系,可以得到GMF中性轴位置珔y和等效惯性矩珔I的计算式:
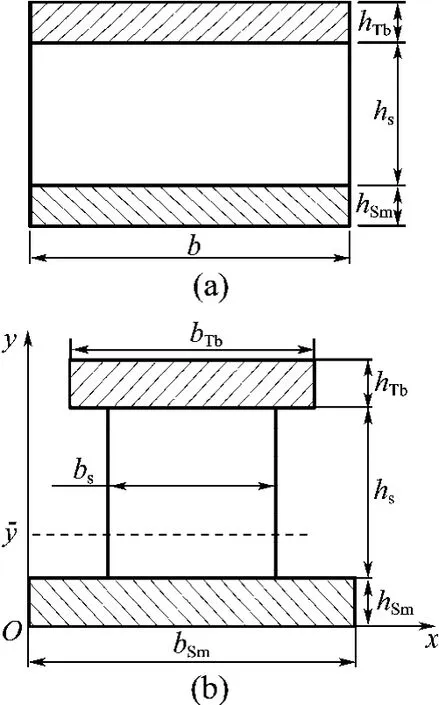
图2 薄膜的当量宽度示意图Fig.2 Sketch of equivalent film width
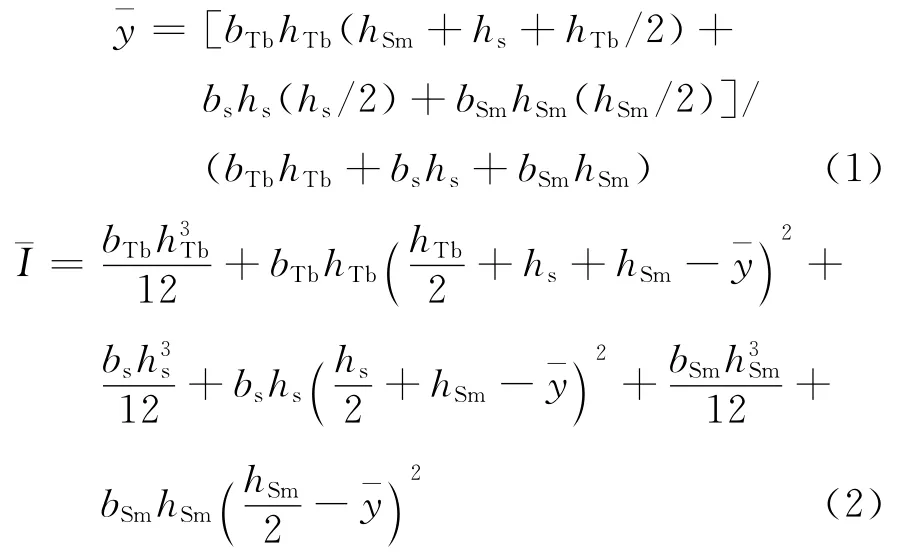
其中hTb、hSm、hs分别为正、负磁致伸缩薄膜和基片的当量厚度;bs为基片宽度,其值等于b.
由式(1)可知,正负复合GMF悬臂梁中性轴的位置与薄膜的宽度无关,分别将项目研究的聚酰亚胺基片、铜基片复合GMF材料的相关参数(见表1)代入式(1),得到以下结果:
①不同宽度的聚酰亚胺基片GMF悬臂梁实验样品的中性轴位置均为珔yPI≈20μm;
②不同宽度的铜基片GMF悬臂梁实验样品的中性轴位置均为珔yCu≈23μm.
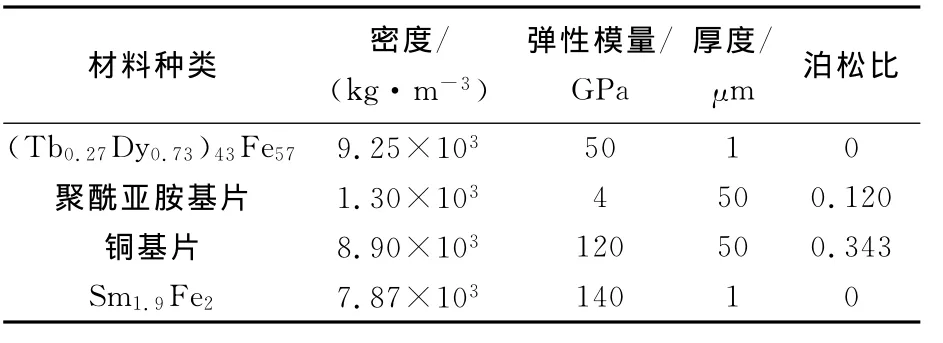
表1 正、负GMF靶材成分和基片的物理性能参数Tab.1 Physical parameters of positive and negative magnetostrictive GMF substrate and target material
在此基础上,将聚酰亚胺基片、铜基片GMF悬臂梁实验样品尺寸参数(见表2)代入式(2),结合式(1)的计算结果得到了各种尺寸实验样品的等效惯性矩和等效抗弯刚度,如表2所示.

表2 各种实验样品的尺寸参数及等效惯性矩、等效刚度的计算结果Tab.2 Calculation results of experiment sample sizes,equivalent inertia moment and equivalent stiffness
1.2 挠曲线方程的求解
磁致伸缩过程是一个非常复杂的过程,磁学量与力学量的耦合系数是一个二阶分量,这使得GMF磁-机械耦合过程的力学分析异常复杂[8].本文采用直接考虑终端变形结果而忽略中间磁致伸缩过程的方法,来研究GMF磁致伸缩过程中力学参数的变化规律,以得出超磁致伸缩复合薄膜磁致伸缩效应作用的机理.
正负复合GMF悬臂梁的结构如图1所示,取其中长度为dx的微分单元结构进行磁致过程中的受力分析[9].假设磁致伸缩过程中,正、负磁致伸缩薄膜产生的磁致伸缩力是绝对均匀分布的,这时微分单元结构的受力情况如图3所示.正磁致伸缩效应薄膜在微分单元两侧产生的拉应力分别为fTb(x)和fTb(x+Δx),负磁致伸缩效应薄膜在微分单元两侧产生的压应力分别为fSm(x)和fSm(x+Δx).
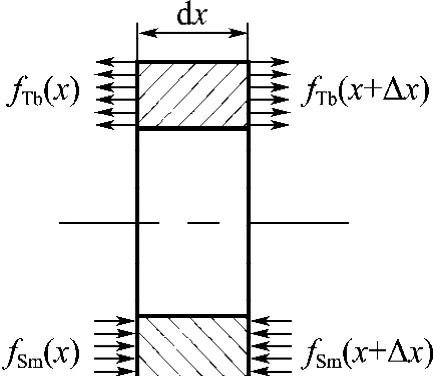
图3 薄膜上微分单元的受力Fig.3 Stress of differential element on film
为了分析方便,本文引入集中力来代替正、负磁致伸缩薄膜产生的均布力.由于正、负磁致伸缩薄膜的弹性模量及产生力的大小不同,超磁致伸缩复合薄膜中性轴的位置已不在薄膜中心轴线上,其结果已在前面的计算中得出.进一步简化微分单元结构上的受力情况,近似地将微分单元的受力等效为作用在单元中性轴的一个弯矩,进而可以得到微分单元所在悬臂梁截面应力分布情况,如图4所示.根据以上的分析结果,可以近似地将悬臂梁式GMF产生的磁致伸缩力简化为薄膜中性轴均布弯矩q的作用.
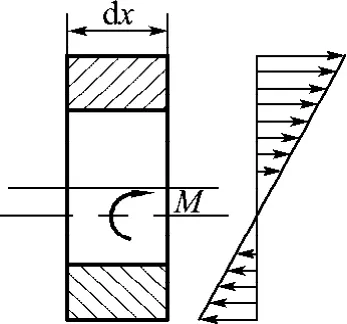
图4 悬臂梁薄膜单元结构受力分析Fig.4 Structural stress analysis of GMF cantilever beam finite element
对于均布弯矩q作用的等截面GMF悬臂梁,根据材料力学的相关知识可导出其挠曲线微分方程的一般形式[10]:
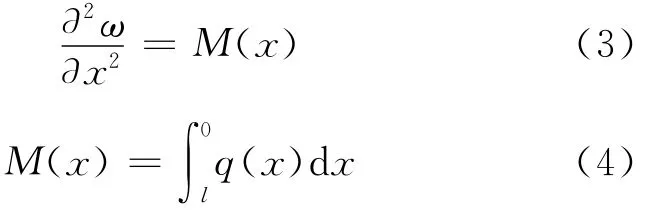
其中ω(x)是挠曲线方程;M(x)是悬臂梁的弯矩方程.
分析GMF悬臂梁的受力变形情况,可得到其边界条件为

求解上述微分方程,可以得出GMF悬臂梁的挠曲线方程为

为了验证上述理论推导,本文首先从微观角度对项目研制的GMF悬臂梁特性进行简要分析.利用吉林大学研制的Jdm-13型振动磁强计进行测量,得到了项目研制的铜基片、聚酰亚胺基片的正负复合GMF平行易磁化轴方向的磁化曲线,如图5所示(σ为单位质量磁矩,Hext为磁场强度).
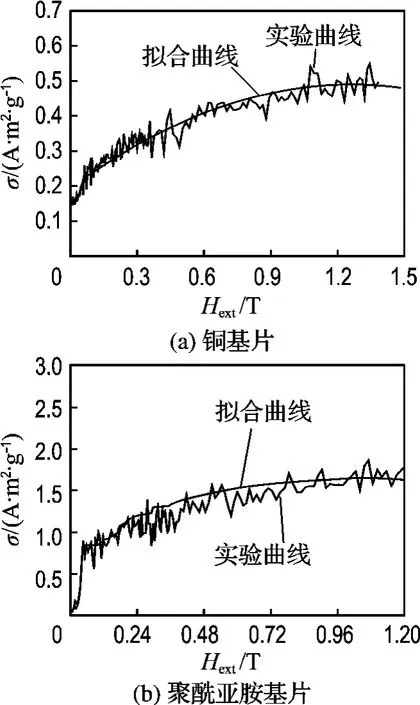
图5 铜基片和聚酰亚胺基片GMF的初始磁化曲线Fig.5 Initial magnetization curves of Cu substrate thin film and polyimide substrate thin film
由图5可以看出,聚酰亚胺基片GMF的磁致伸缩能力较强,其等效抗弯刚度较小,与前面求得的结果是相同的.此外,从图上可以看出,这两种GMF的初始磁化曲线呈现出了一定的线性关系.
2 薄膜悬臂梁的静力学实验
为了进一步验证前面理论结果的正确性,项目设计了相应的实验对3种不同结构尺寸的复合薄膜悬臂梁的变形情况进行研究.实验系统结构如图6所示,主要包括日本产高性能稳压电源Bp4610、亥姆霍兹驱动线圈、美国产MicrotrakII激光测微仪、悬臂梁夹头、美国产7030高斯计、示波器以及工作电脑等.其中亥姆霍兹驱动线圈为自制设备,主要参数有:内孔半径18 mm,外孔半径59.5 mm,单线圈宽度100 mm,线圈间距40 mm,单线圈匝数1 665,组合线圈电阻9.8Ω.

图6 实验装置Fig.6 Experimental setup
实验对悬臂梁在同一磁化状态下不同位置的偏移量进行了测量,并通过曲线拟合得出了悬臂梁的挠曲线.在线圈驱动电压为30 V,磁感应强度为27.4 m T时,分别得到聚酰亚胺基片、铜基片GMF悬臂梁的挠度实验曲线与拟合曲线.其中,图7(a)是长度38 mm、宽度3 mm的聚酰亚胺基片GMF悬臂梁磁致伸缩挠度的实验曲线与拟合曲线.图7(b)是长度30 mm、宽度3 mm的铜基片GMF悬臂梁磁致伸缩挠度的实验曲线与拟合曲线.在驱动电压30 V、驱动磁场192 mT时,得到长度30 mm、宽度3 mm的铜基片GMF悬臂梁磁致伸缩挠度的实验曲线与拟合曲线,如图7(c)所示.
从图7中拟合曲线方程的形式可以看出,3种情况下GMF悬臂梁磁致伸缩挠度方程的形式均为δ(x)=Ax3-Bx2的形式,其中A、B为与磁致伸缩效应有关的常数.拟合曲线形式与理论推导的超磁致伸缩复合薄膜悬臂梁挠度曲线方程式(7)的形式是一致的,可以证明理论分析方法和结论是正确的.在不考虑薄膜ΔE效应的前提下,根据悬臂梁超磁致伸缩复合薄膜结构挠度分析结果,可以认为薄膜的机械变形与薄膜产生的磁致伸缩力呈线性关系,即磁致伸缩过程中薄膜的磁学量与力学量呈一定的线性关系,研究的结果为动态磁致伸缩效应的进一步分析研究奠定了理论基础.
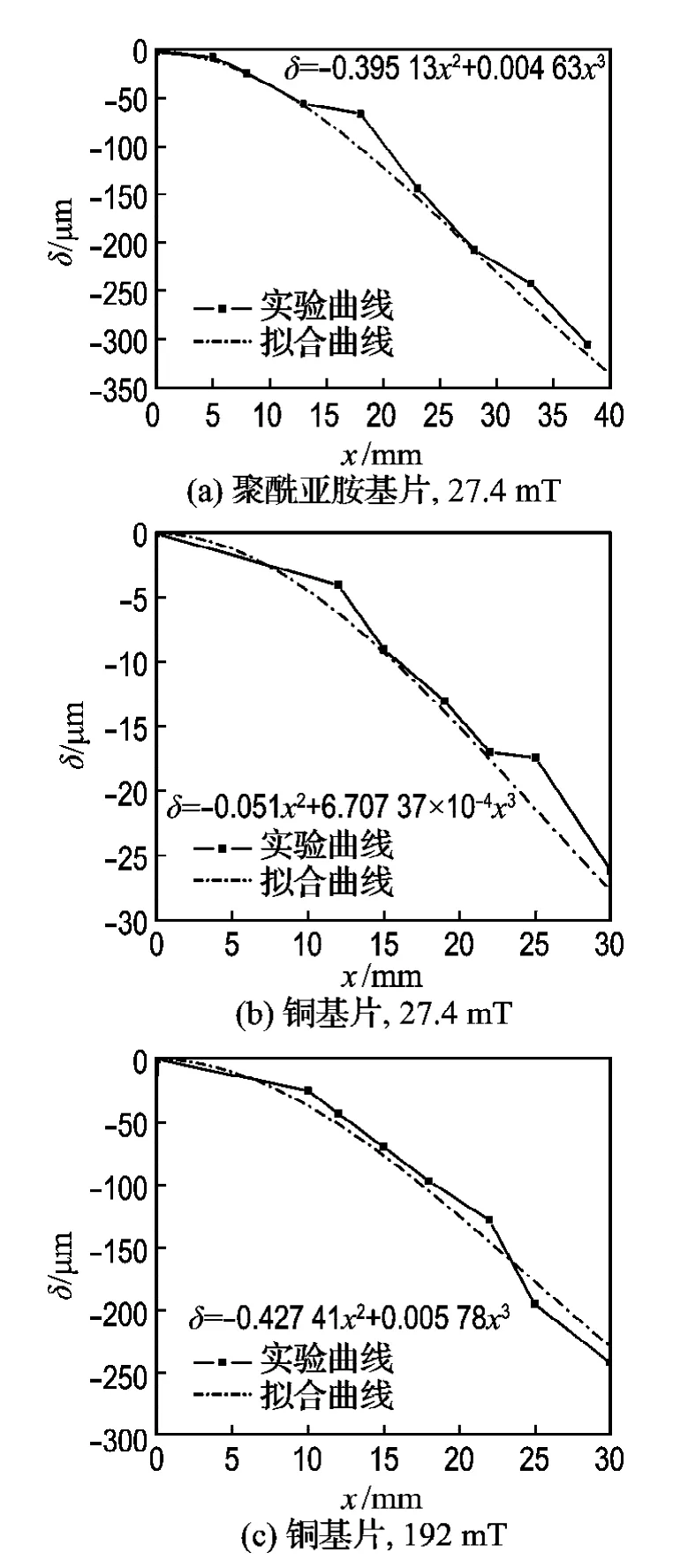
图7 GMF悬臂梁的挠度曲线Fig.7 Deflection curves of GMF cantilever beam
3 结 论
本文结合材料力学的相关理论,对GMF悬臂梁进行了静力学特性分析.在求解不同材料双层薄膜悬臂梁中性轴的基础上,建立了其在静态磁场作用下的挠曲线方程;进一步对不同基底材料和尺寸形状的悬臂梁进行了实验研究,结果表明本文的理论分析是正确的,所以通过材料力学的一般原理也可近似完成对GMF材料的理论分析.此外,本文的研究也表明磁致伸缩过程中薄膜的磁学量与力学量呈一定的线性关系,这一结论为动态磁致伸缩效应的进一步分析研究奠定了理论基础.
[1]GUERRERO V H,WETHERHOLD R C.Strain and stress calculation in bulk magnetostrictive materials and thin films[J].Journal of Magnetism and Magnetic Materials,2004,271(2-3):190-206
[2]DEAN J,GIBBS M R J,SCHREFL T.Finiteelement analysis on cantilever beams coated with magnetostrictive material[J].IEEE Transactions on Magnetics,2006,42(2):283-288
[3]KAVIRAJ B,GHATAK S K.Simulation of stressimpedance effects in low magnetostrictive films[J].Journal of Non-Crystalline Solids,2007,353(16-17):1515-1520
[4]LEE H S,CHO C.Study on advanced multilayered magnetostrictive thin film coating techniques for MEMS application[J].Journal of Materials Processing Technology,2008,201(1-3):678-682
[5]ISHIYAMA K,YOKOTA C.Cantilevered actuator using magnetostrictive thin film[J].Journal of Magnetism and Magnetic Materials,2008,320(20):2481-2484
[6]TIERCELIN N,PREOBRAZHENSKY V,MORTET V.Thin film magnetoelectric composites near spin reorientation transition[J].Journal of Magnetism and Magnetic Materials,2009,321(11):1803-1807
[7]ROARK R J,YONG W C.应力应变公式[M].北京:中国建筑工业出版社,1985
[8]王福吉.正负超磁致伸缩复合薄膜静动态特性及控制关键技术[D].大连:大连理工大学,2005
[9]刘廷柱,陈文良,陈立群.振动力学[M].北京:高等教育出版社,1998
[10]王守新.材料力学[M].大连:大连理工大学出版社,2004

