转子－齿式联轴器－轴承系统不对中动力学特性

赵 广， 郭嘉楠， 王晓放， 刘占生

（1.大连理工大学能源与动力学院，辽宁大连 116024；2.哈尔滨工业大学能源学院，黑龙江哈尔滨 150001）

0 引 言

大型旋转机械中转子故障是关系到生产安全的重要问题，其中不对中故障占转子系统故障的60%以上［1］.不对中状态下转子运动将引起机械振动、轴承的磨损、轴的挠曲变形、转子与定子间碰摩等，同时，不对中会直接改变转子系统的稳定性.因此系统地开展不对中对转子－联轴器－轴承系统动力学特性和稳定性的研究对于大型旋转机械的安全稳定运行和故障诊断具有重要的意义.

大多数旋转机械由驱动部件和被驱动部件组成，中间通过各种联轴器的联接来传递扭矩［2］.目前工业用的联轴器有很多种，其中齿式联轴器可以传递较高负载并且可以调整两转子的不对中，因此常用于船舶驱动轴、汽轮机等大型工业设备中［3］.尽管如此，齿式联轴器复杂结构、较大负载及加工安装误差，以及转子变形、轴承不同心和机座高低偏差等，不可避免地导致被连接的两转子产生不对中.不对中的存在导致其运动过程中产生一系列的不利于设备运行的动态效应，使旋转机械的振动变得复杂，有时候很难做出合理解释［4］.

文献［5、6］研究了鼓形齿式联轴器的角向自激振动问题，Al－Hussain［4］研究发现倾角不对中或者联轴器刚度增加会增加系统的稳定性.李明［7］的研究表明平行不对中转子系统是一个具有自激振动特征的强非线性系统，不对中对轴心轨迹、振动频率成分具有重要的影响.文献［8］指出当联轴器处于对中和良好润滑状态时，其内阻尼对失稳转速影响较小.

本文推导齿式联轴器不对中啮合力模型，建立不对中转子－齿式联轴器－轴承系统非线性动力学方程，通过Newmark数值仿真预测系统的不对中动力学特性和稳定性，并建立转子－齿式联轴器－轴承系统实验台进行实验验证.

1 齿式联轴器不对中啮合力模型

在润滑良好的情况下，忽略齿面间的摩擦，轮齿的啮合刚度主要与单齿的弹性变形有关［9、10］.参考作者在文献［11］中对于齿式联轴器不对中啮合力模型的研究，单个轮齿在啮合点处单位荷载作用下的弹性变形δj主要包括悬臂梁（轮齿）的变形δbj、弹性基础的变形δmj、齿面啮合点处的接触变形δcj.单齿啮合刚度

单齿啮合刚度除了与联轴器各参数有关外，还与各齿啮合点到齿根的距离即啮合距离L j有关.考虑系统的静态不对中（e0，φ0）和动态不对中（x，y），实际不对中（e，φ）为

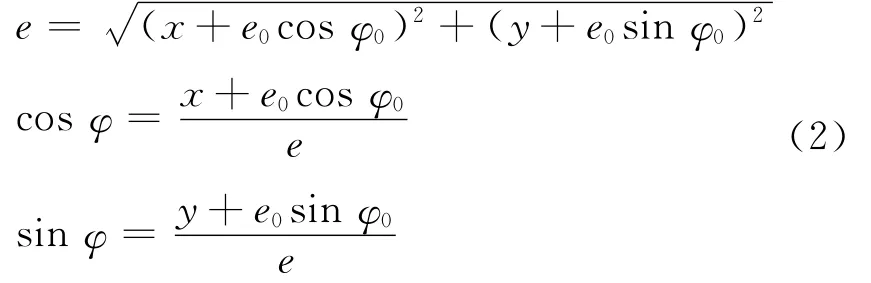
各齿等效啮合距离

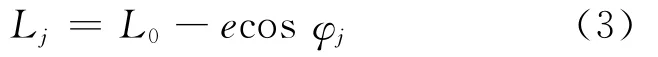
φj＝2π（j－1）／z，为各齿与x轴正向的夹角.

在转子 －联轴器－轴承系统中，联轴器传递扭矩使轮齿产生一个变形，即扭转使各齿产生一个啮合力

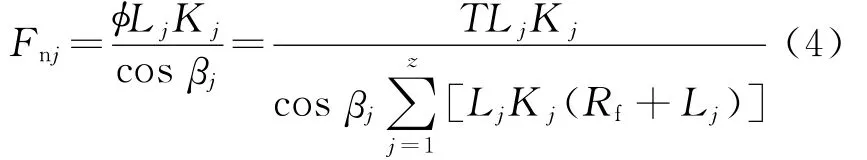
T为联轴器传递扭矩，Rf为联轴器齿根圆半径.

由于内、外联轴器随系统各自振动时，内外联轴器的啮合又使各齿产生一个变形，即动态振动位移使各齿产生一个啮合力，其表达式为

综上，联轴器由于不对中而产生的啮合力为

由于振动作用，联轴器整圈齿中，编号为1～z／2的各齿啮合力变大，其余变小，但每一个齿的啮合力均不会为负，因此，当传递扭矩为0时，即使存在动态振动位移，也不会产生啮合力.即

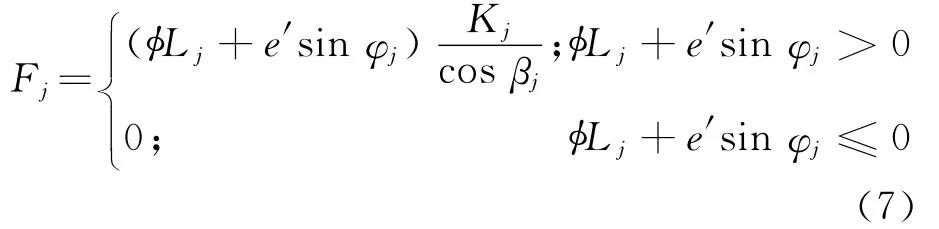
则不对中使整个联轴器产生的x、y向合力为

其中θj为每个齿作用力方向与x轴正向的夹角，根据以上推导可知

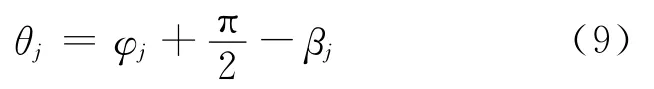
考虑实际不对中发生的角度φ，联轴器不对中啮合力为

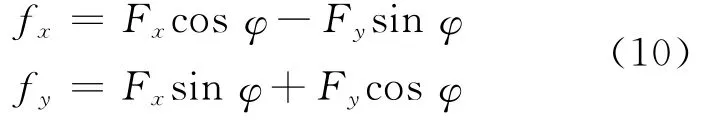
从齿式联轴器不对中啮合力模型推导看出，该力是一个复杂的非线性函数，不但与联轴器结构参数有关，还与被连接系统的传递扭矩、静态不对中、动态不对中等有关.

2 转子－联轴器－轴承系统动力学模型

转子－联轴器－轴承系统结构示意图如图1所示.采用有限元法将系统划分为19个轴段，20个节点，共计80个自由度.4个滑动轴承分别位于节点2、10、12和19.

图1 转子－联轴器－轴承系统结构示意图

Fig.1 Structure sketch of rotor－coupling－bearing system

基于有限元法，采用Eular－Bernouli梁模型假设，得到该系统的动力学方程如下：

式中：M、C、K分别为系统质量、阻尼（取比例阻尼）、刚度阵；JΩ为转子的陀螺力矩阵；Z＝（x ky k－θxkθyk）（k为节点编号）为节点位移向量；G、Q（t）分别为重力和不平衡力项；F（z，Ω）为滑动轴承非线性油膜力，本文采用修正的短圆柱瓦轴承非线性油膜力解析模型［12］.

Fc为齿式联轴器动态啮合力.由式（10）可得

设dx、dy分别为内、外联轴器所在节点的相对位移，上式各符号含义如下：

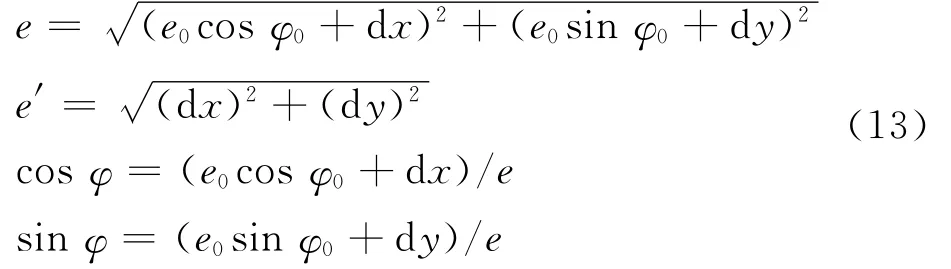
不对中联轴器的外齿套偏心将产生不平衡激励，激励频率为转频的2倍，表达式为［5］

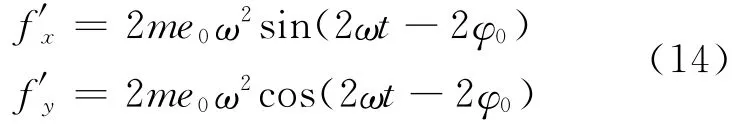
其中m为联轴器外壳质量.

联轴器啮合力和油膜力均为典型的非线性项，因此式（11）是复杂的多自由度非线性方程.目前对该方程求解唯一有效的方法是数值仿真法.Newmark－β逐步积分法计算效率高、稳定性好，因此本文采用该方法求解系统的动力学响应.

3 齿式联轴器不对中动力学特性

本文研究的齿式联轴器型号为GICLZ3，其结构参数如表1所示.

3.1 静态不对中动力学特性

设转子－齿式联轴器－轴承系统不平衡量发生在某一特定轮盘上，其大小和方向一定.当不对中量为0～0.8 mm且位于垂向时，3 000 r／min时轴承3＃处转子频谱图如图2所示.

表1 齿式联轴器参数Tab.1 Parameters of gear coupling

图2 不同静态不对中量下轴承3＃频谱图Fig.2 Frequencies of bearing 3 with different static misalignments

结果表明，一定不平衡力下，静态不对中量增加会导致各轴承x、y向2X倍频振幅显著增加，1X倍频振幅也有所增加；不对中量继续增加，系统将出现3X、4X高倍频振动.

3.2 动态不对中动力学特性

不平衡和基础支撑柔性是导致转子系统产生动态不对中的根源.在上述静态不对中量为0、0.4 mm的基础上，仅将不平衡量大小增加3倍，即改变系统的动态不对中量，相同位置处转子频谱图如图3所示.

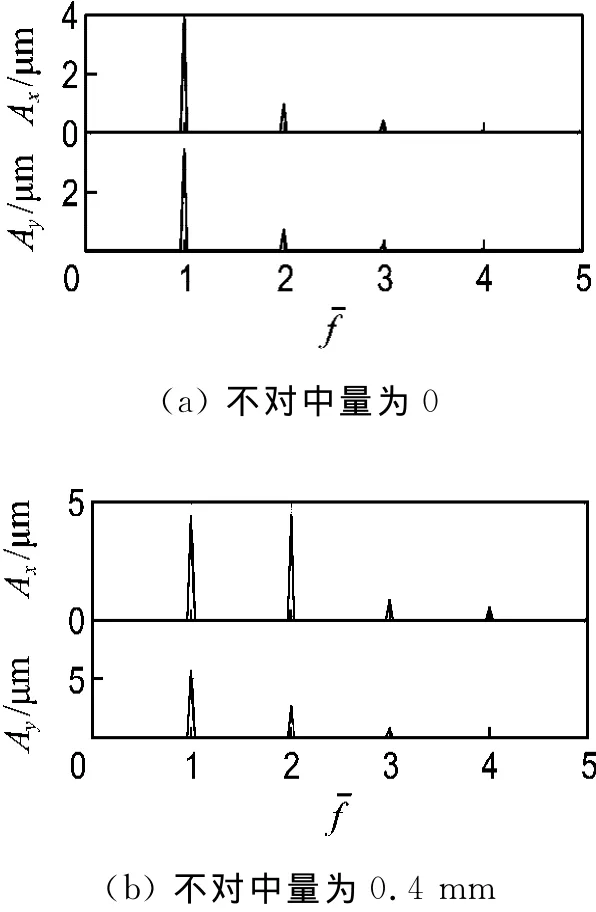
图3 不同动态不对中量下轴承3＃频谱图Fig.3 Frequencies of bearing 3 with different dynamic misalignments

动态不对中变化前后转子响应对比表明，当静态不对中保持不变时，增加动态不对中联轴器两边轴承x、y向的1X、2X倍频振动均增大.因此动态不对中量的增加，同样会导致系统2X倍频振幅的增加.

4 齿式联轴器不对中稳定性

转子响应的幅频特性曲线、三维谱图、分岔图等是研究系统失稳的基本手段，在0～1.2 mm范围内改变转子不对中量，轴承1＃响应结果如图4～6所示.

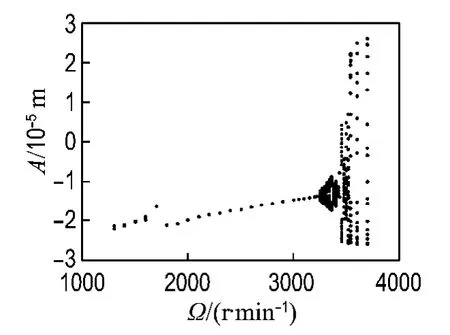
图4 不对中量为0时轴承1＃y向分岔图Fig.4 Bifurcation of bearing 1y with 0 misalignment

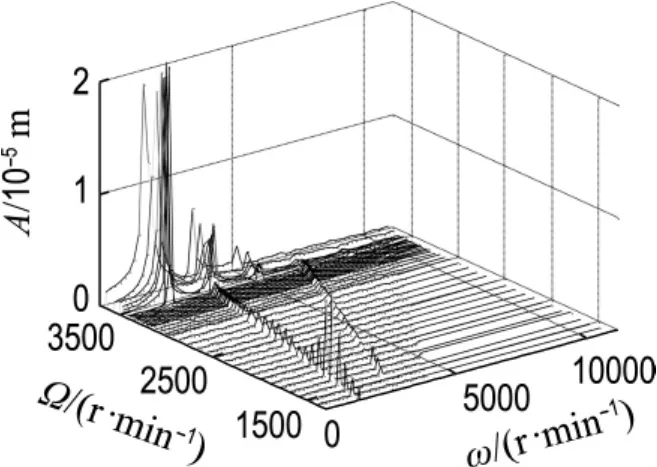
图5 不对中量为0.4 mm时轴承1＃y向三维谱图Fig.5 Waterfall of bearing 1y with 0.4 mm misalignment

完全对中时，在3 380 r／min之前，转子振幅较小，转速稍微提高则通频振幅急剧增加，出现振幅突跳，系统出现拟周期分岔，并进入锁频状态，导致失稳.因此，对中状态下系统失稳转速为3 380 r／min.

不对中量为0.4 mm时，在3 400 r／min以前，以基频振动为主，之后出现0.5X低频涡动，油膜力非线性效应增强；转速提高至3 460 r／min时低频振幅剧增，转子非同步涡动频率不随转速增加，而是保持在转子一阶临界转速附近，油膜涡动发展为油膜振荡.因此，该状态下系统失稳转速为3 460 r／min.

图6 不同不对中量下轴承1＃幅频特性Fig.6 Amplitude－frequency of bearing 1 with different misalignment

整理各状态下的失稳转速如图7所示.转子－联轴器－轴承系统的失稳转速Ω′随着不对中量的增加先稍微增加，而后显著降低.究其缘由为，较小不对中量时，联轴器偏心占主导作用，因为适当的小偏心会提高转子系统的稳定性［13］；而较大不对中状态下，联轴器不对中啮合力起主导作用，啮合力间接改变了轴承负载分布，即2＃轴承负载降低并引起系统稳定性降低.综上，转子－联轴器－轴承系统稳定性与不对中密切相关.

图7 失稳转速随不对中量变化的曲线Fig.7 Threshold speeds of stability versus misalignments

5 齿式联轴器不对中试验研究

5.1 实验台的建立

转子－联轴器－轴承系统实验台实物图如图8所示，其由驱动、润滑、转子－联轴器－轴承系统、信号采集与处理系统等构成；两个单转子分别采用圆柱瓦滑动轴承支撑，并通过齿式联轴器连接起来，驱动部件振动通过柔性绳子连接予以消除.

图8 转子－齿式联轴器－轴承系统实验台Fig.8 Test rig of rotor－gear coupling－bearing system

不对中通过轴承标高调节装置实现，如图9所示，可线性、连续精确调节轴承支承标高并采用百分表测量实现.齿式联轴器及其组成部件如图10所示.

图9 轴承标高调节装置Fig.9 Adjustor of bearing elevation

图10 齿式联轴器及其组成部件Fig.10 Gear coupling and its components

转子轴承处的振动通过8个位移传感器测量实现，分别测量轴承附近转子的x、y向振动位移，转速通过键槽触发，信号采集系统如图11所示.

5.2 齿式联轴器不对中动力学特性

为了使各状态具有可比性，试验过程中固定转子1的轴承支承标高，同时调节转子2的两个轴承标高在0～0.8 mm，各状态轴承3＃y向试验结果三维谱图如图12所示.

图11 信号采集与处理系统Fig.11 Signal acquisition and processing system

结果表明，对中系统的振动以1X倍频振动为主，基本不存在其他频率成分的振动；当不对中量为0.4 mm时，升速至2 800 r／min以后，出现2X、3X倍频振动，但振幅较小；随着不对中量的增加，2X、3X振幅明显增加，不对中量为0.8 mm时开始出现较大的4X倍频振动.

数值仿真和试验研究均较为一致地预测出不对中转子系统的倍频振动，及倍频振动随不对中量增加而增加的规律.数值仿真中，2X倍频变化比较显著，而试验结果存在着各种倍频振动，这种差别源于数值仿真引入的基础刚性、阻尼线性、驱动电机的理想化等假设.

5.3 齿式联轴器不对中稳定性

转子－齿式联轴器－轴承系统对中状态下升、降速过程振动三维谱图如图13、14所示.

升速试验中，在3 050 r／min以后，转子1（轴承2＃y向）出现油膜的半速涡动，而转子2（轴承3＃y向）只有工频振动；升速至3 302 r／min时，转子2突然出现巨大的0.687 5X倍频低频振动.电机保护，自然降速、停机，降速时转子1、2均出现典型的锁频现象，如图13（b）、14（b）所示.转子1、2的频率分别锁定在各自的一阶临界转速附近，转子1在降速至2 924 r／min以后出现，而转子2在整个降速过程中油膜锁频现象显著.

综上，转子1出现了油膜涡动，但尚未出现振荡；转子2未发生油膜失稳，而是在3 302 r／min出现低频自激振荡导致的失稳，该失稳是齿式联轴器导致的.因此，齿式联轴器的自激振荡是诱发转子－轴承系统失稳的因素之一，在一定的状态下，联轴器诱发的失稳先于滑动轴承非线性油膜力诱发的失稳.综上，对中系统的失稳转速为3 302 r／min.

增大系统的不对中量，各状态转子2（轴承3＃）、转子1（轴承2＃）振动响应的三维谱图分别如图15、16所示.

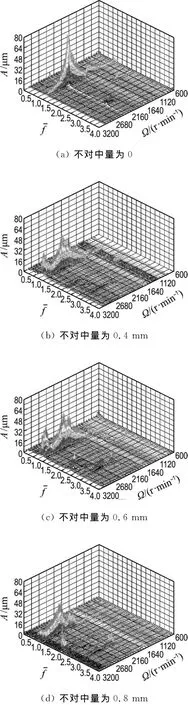
图12 不同不对中量下轴承3＃y向三维谱图Fig.12 Waterfall of bearing 3y with different misalignments

图13 轴承2＃y向升、降速试验三维谱图Fig.13 Waterfall of bearing 2y with run－up and run－down experiment

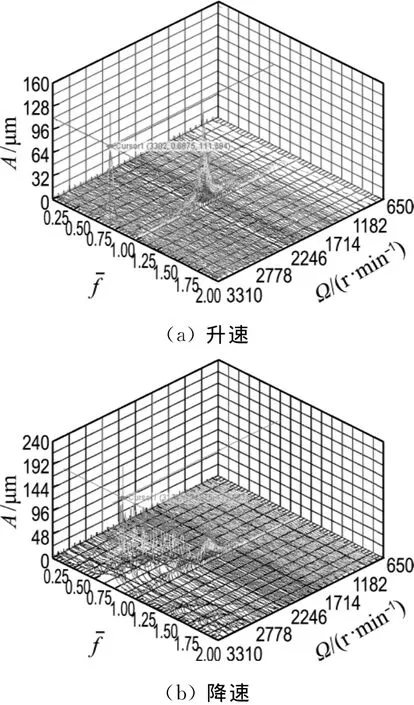
图14 轴承3＃y向升、降速试验三维谱图Fig.14 Waterfall of bearing 3y with run－up and run－down experiment

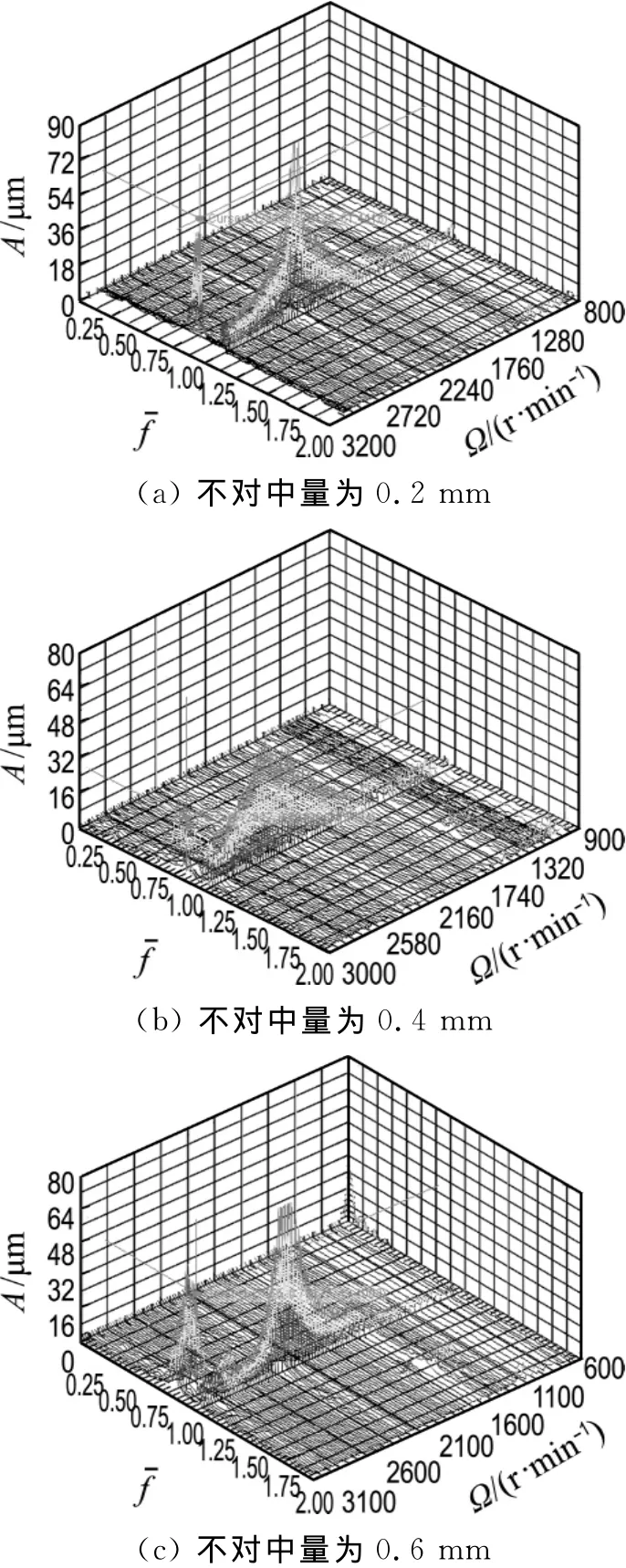
图15 不同不对中量下转子2响应三维谱图Fig.15 Waterfall of rotor 2 with different misalignments

采用同样的分析方法，状态2的系统出现了齿式联轴器自激振荡导致的转子2失稳，低频振荡频率为0.78X，失稳转速为2 984 r／min；而状态3的联轴器自激振荡失稳转速为2 922 r／min；状态4中，转子1在3 080 r／min时出现油膜振荡失稳，而转子2在2 866 r／min时出现联轴器自激振荡失稳；状态5、6中，只有转子1的油膜振荡失稳.失稳转速汇总如表2所示.

综合以上分析，转子1主要发生油膜失稳，不对中量较小时，油膜失稳随不对中量增加有所提高，不对中量较大时基本保持不变；而转子2为联轴器自激振荡失稳，随着不对中量增加，稳定性明显降低.试验过程中，以上两种失稳形式交替出现或者同时出现，两种非线性激励耦合作用于系统的稳定性.

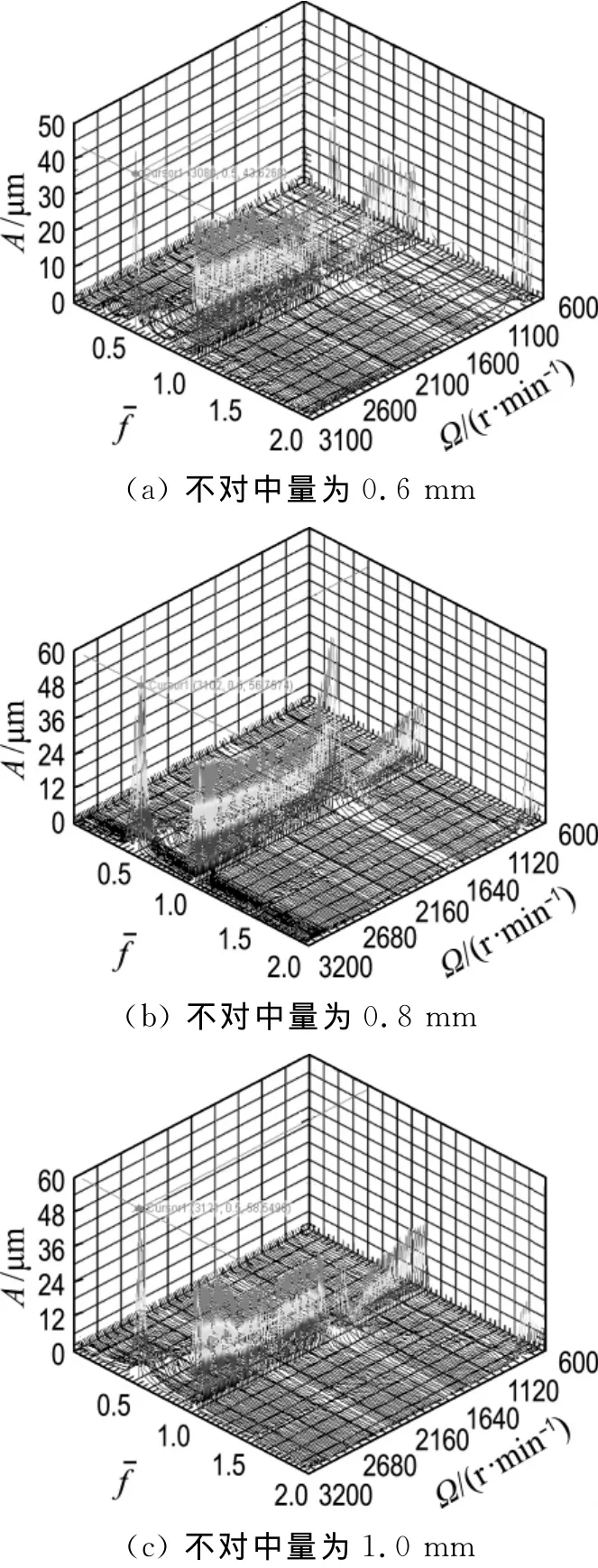
图16 不同不对中量下转子1响应三维谱图Fig.16 Waterfall of rotor 1 with different misalignments

表2 转子－齿式联轴器－轴承系统失稳转速

Tab.2 Stability threshold speed of rotor－gear coupling－bearing system

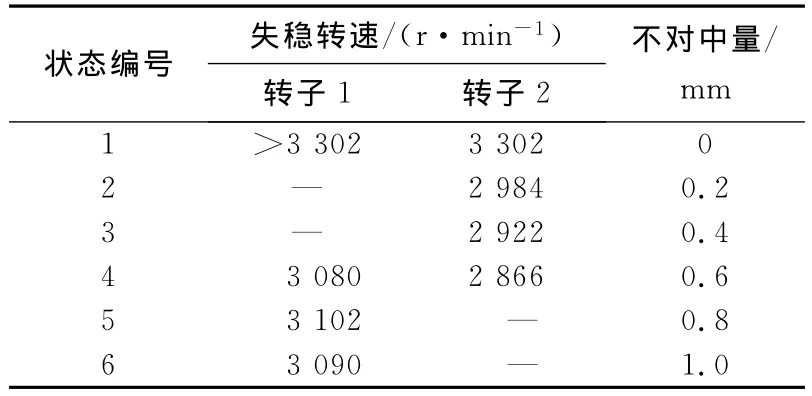
状态编号 失稳转速／（r·min－1）转子1 转子2不对中量／mm 1＞3 302 3 302 0 2—2 984 0.2 3—2 922 0.4 4 3 080 2 866 0.6 5 3 102 — 0.8 6 3 090 —1.0

对比仿真试验结果发现，在预测油膜稳定性方面，二者具有很好的吻合性，而试验结果更好地揭示了油膜振荡和联轴器自激振荡的耦合机理.这种差别源于联轴器建模中忽略了齿面的摩擦，需要进一步改进.

6 结 论

（1）虽然齿式联轴器具有一定的不对中补偿能力，静、动态不对中均会导致系统倍频振动的出现，且随着不对中量的增加而增加.因此，转子－联轴器－轴承系统中，不平衡故障和不对中故障常常会耦合起来，同时出现.

（2）转子－齿式联轴器－轴承系统中，油膜失稳发生在系统一阶临界转速的2倍附近；随着不对中的出现和增加，油膜力和联轴器啮合力会交替或耦合降低系统的稳定性.

（3）转子－齿式联轴器－轴承系统中，不平衡、不对中、失稳故障常常会相互影响，互相耦合影响系统的动力学特性，因此在对该系统进行故障诊断时，应充分考虑齿式联轴器和滑动轴承的耦合效应.

［1］JACKON C.Successful shaft hot alignment［J］.Hydrocarbon Processing，1969（6）：28－40

［2］AL－HUSSAIN K M，REDMOND I.Dynamic response of two rotors connected by rigid mechanical coupling with parallel misalignment［J］.Journal of Sound and Vibration，2002，249（3）：483－498

［3］LI M，YU L.Analysis of the coupled lateral vibration of a rotor－bearing－system with a misaligned gear coupling［J］.Journal of Sound and Vibration， 2001，243（2）：283－300

［4］AL－HUSSAIN K M.Dynamics stability of two rigid rotors connected by a flexible coupling with angular misalignment［J］.Journal of Sound and Vibration，2003，266（2）：217－234

［5］山內進吾，染谷常雄.齒車繼手の研究［J］.日本機械學會論文集，1980，46（407）：806－814

［6］山內進吾，染谷常雄.齒輪聯軸器軸系的自激振動［J］.齒輪，1984，8（6）：49－52

［7］李 明.平行不对中转子系统的非线性动力学行为［J］.机械强度，2005，27（5）：580－585

［8］李 明，虞 烈，沈润杰.齿轮联轴器对轴承转子系统失稳转速的影响［J］.发电设备，2000（3）：26－28

［9］周长江，唐进元，吴运新.齿根应力与轮齿弹性变形的计算方法进展与比较研究［J］.机械传动，2004，28（5）：1－6

［10］TAVIKOLI M S，HOUSER D R.Optimum profile modification for the minimization of static transmission errors of spur gear［J］.ASME，Journal of Mechanisms，Transmissions and Automation in Design，1986，108：86－94

［11］赵 广，刘占生.齿式联轴器不对中啮合力产生机理及其对转子系统动力学特性影响［J］.哈尔滨工程大学学报，2009，30（1）：33－39

［12］ADILETTA G，GUIDO A R，ROSSI C.Chaotic motions of a rigid rotor in short journal bearings［J］.Nonlinear Dynamics，1996，10：251－269

［13］张 野.汽轮机转子－轴承系统非线性动力学研究［D］.哈尔滨：哈尔滨工业大学，2007