金属熔池往复搅拌流场中气泡运动特性数值模拟研究
刘 红, 解茂昭, 于 静, 王德庆
(1.大连理工大学能源与动力学院,辽宁大连 116024;2.大连交通大学材料工程学院,辽宁大连 116028)
0 引 言
泡沫铝是一种新型的功能材料,如何获得大小均一、分布均匀的气泡结构是泡沫铝制备技术中的关键问题.应用平行往复运动的吹气头代替旋转搅拌设备在铝熔液中吹气发泡,能够使生成的气泡尺寸更加均匀,且熔池液面附近不会形成强的涡流,有利于形成稳定的“干泡沫”被牵引出熔池,冷却后得到品质更好的泡沫铝成品.单个气泡在静态液体[1~3]或旋转搅拌流场[4、5]中的运动行为现已有研究.搅拌头平行往复运动条件下,单个气泡的运动特性与熔池静止及旋转流场条件下有所不同,包括气泡运动轨迹,气泡的变形、破碎等因素,但公开发表的文献中,迄今尚未发现相关的理论和数值模拟研究的报道,本文利用数值方法分析气泡在平行往复运动流场中的运动特性及其影响因素.
1 数学模型及求解方法
1.1 控制方程组
在模型中,无论是气泡外部的液相流体还是气泡内部的气相均应遵守质量、动量和能量守恒.本文设气液两相温度相同,没有温度变化,故不考虑能量方程.假设:(1)气液界面无表面活性剂;(2)气液界面无相变发生;(3)气液两相流体是不可压缩牛顿流体;(4)不考虑传质、传热;(5)流动为层流流动.则控制方程为式中:Fbf表示两相流体的界面力,在此主要考虑两相界面处的表面张力.表面张力的具体计算方法在1.2中讨论.当计算单元中是液体或气体时,方程中的流体物性为相应液体或气体的物性.当计算单元内包含两相界面时,流体物性按照两相体积分数的加权平均进行计算,即

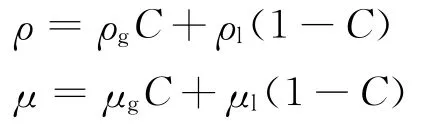
1.2 界面跟踪方法
两相流体在界面处主要受到表面张力的作用,为正确表达表面张力,必须给出界面曲率,也就是需要对两相运动界面进行合理跟踪并描述.目前两相界面跟踪方法主要有基于拉格朗日网格系统的前跟踪法(front-tracking method)和基于欧拉系统的体跟踪法.基于体跟踪的VOF(volume of fluid)方法[6]通过引入指定的函数(体积分数),在网格不变的情况下实现界面重构,从而可以较准确地跟踪气液两相界面的拓扑结构变化[7、8].
在VOF方法中引入气含率C代表单元控制体(cell)内气体的体积分数,气含率的取值为

通过控制单元内及与之相连控制单元内的C值,利用分段线性界面计算方法(PLIC)即可通过重构技术得到气泡界面,从而确定其形状及尺寸.通过连续表面张力模型(CSF模型)计算作用在气液两相界面的力
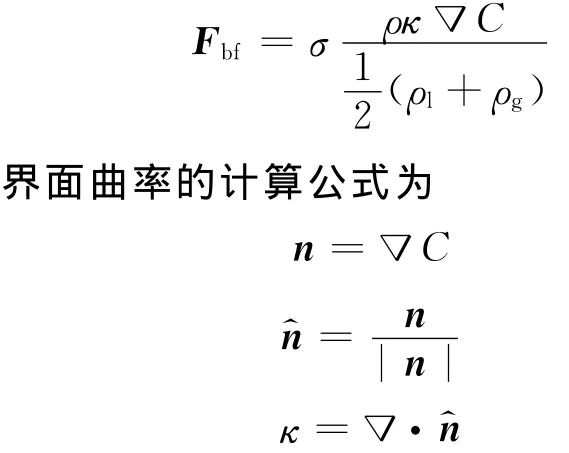
1.3 搅拌器平动模型
实验及数值试验证明,吹气头平行往复运动产生的剪切力会促进更加均匀的小气泡生成,同时吹气头平行移动使得生成的气泡与此吹气头生成的前一个气泡不在同一上升路径上,从而避免了气泡间的聚合.因此本文提出应用平行往复吹气头代替旋转吹气头,吹气头由曲柄连杆结构实现其平行往复运动,其运动规律与曲柄连杆结构带动的活塞运动规律相似.文献中对静止液体[9],均匀横向、纵向剪切流[10]以及旋转流场[11]中气泡的生成及上升过程运动特性分析较多,但往复脉动流场中气泡的运动特性至今尚未见报道.
本文不研究气泡生成,只分析吹气头平行往复运动时气泡上升过程的运动特性,曲柄连杆结构带动的吹气头在熔池内只有水平方向运动,吹气头在水平方向的运动规律为

式中:R是曲柄半径;ω是曲柄转动速度,rad/s;α是曲柄转角,rad;L是连杆长.曲柄连杆设计为R=14 mm,L=300 mm.吹气头在熔池内的运动过程应用运动网格系统来描述,该坐标系以上述吹气头的运动规律作水平往复运动.在此坐标系内,刚性的吹气头及与其表面相接触的液体均为零速度,从而满足了吹气头的边界条件,保证了流固两相的耦合.而熔池两侧壁面及底面则是绝对静止不动的.
2 模拟结果分析
本文应用商用软件Fluent 6.0解上述方程,压力-速度耦合用SIMPLEC相间耦合格式,压力的离散用PRESTO格式,动量方程用二阶迎风格式,体积分数方程应用结构重组格式.
由于未见往复脉动流场中气泡运动特性分析的文献报道,为验证模型的可靠性,应用上述模型(不包括平动模型)对文献[7]所做静止流场内的气泡运动特性实验进行模拟(计算条件参见文献[7]),并将模拟结果与文献中的实验结果及数值模拟结果进行比较.为使模拟结果具有可比性,本文采用与文献[7]相同的二维轴对称模型,图1为本文气泡上升速度模拟结果与文献[7]中的实验结果及数值模拟结果的对比情况.可以看出,本文模拟结果与文献[7]实验结果及数值模拟结果吻合较好.
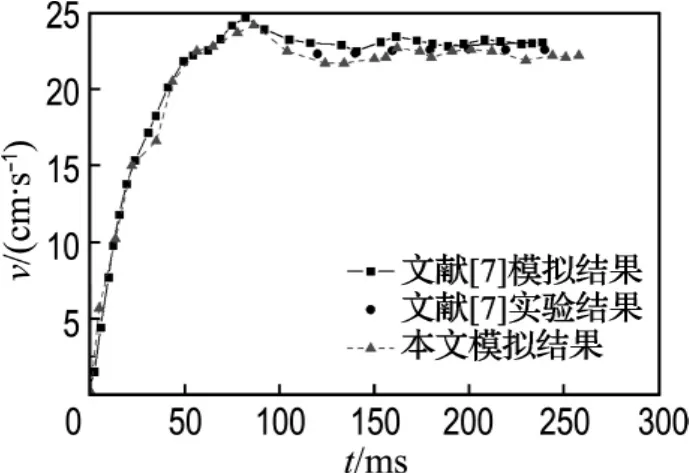
图1 气泡上升速度结果比较Fig.1 Results comparison of bubble rising velocity
由文献[9]可知,实际气泡在静止液体中的运动过程并非直线上升,而是螺旋上升.同时为描述搅拌头往复运动,本文应用二维平面模型代替二维轴对称模型模拟气泡在液体内的上升过程及形状变化.计算区域为130 mm(宽)×200 mm(高),其内放置正方形水平方向平行往复运动吹气头(10 mm×10 mm),吹气头下表面距离底面20 mm,吹气头在水平中心位置横向速度最大.气泡初始位置在水平中心线上,距底面35 mm,气泡初始直径分别为4、6、8 mm.容器内气液两相位于与刚性体具有相同水平往复运动速度的坐标系内,在吹气头作用下平行往复运动,容器左右边界及下底面均为绝对静止无滑移壁面,上表面为压力出口边界条件,出口压力为1×105Pa.控制体网格为非均匀结构化网格,应用3种不同的网格对上述几何模型进行模拟,其中Case1网格数为320×500,Case2网格数为280×435,Case3网格数为240×350.由于气泡直径较小,要求网格较细才能有效捕捉到两相界面,气泡轨迹范围内网格较细,其他位置只有单相液体,对网格要求不高,网格相对较粗.时间步长为1.67×10-5s,其选择与吹气头平动频率有关,各相收敛残差小于10-5.数值模拟中,液相为铝熔体,气相为空气,两相流体的物性如表1所示.
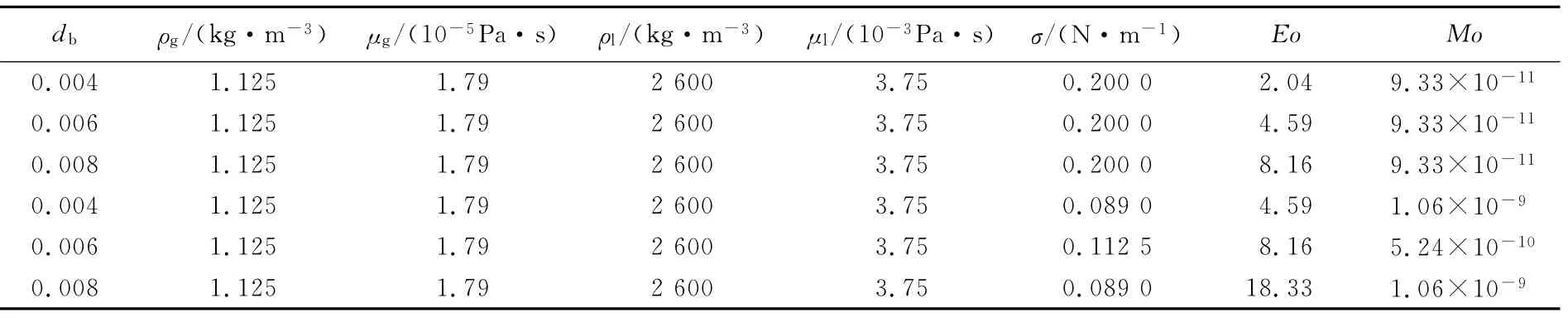
表1 空气及液态铝的物性Tab.1 Physical properties of bubble and molten aluminum
首先考查网格对计算结果的影响,图2示出平动频率为0(即液体静止)时不同网格下气泡上升速度的对比.可见网格密度对计算结果会有一定的影响.Case3的计算结果与其他两种网格的计算结果差别较大,Case1和Case2上升速度则相差不大.均衡计算时间及计算精度,以下计算均采用Case2网格,即网格数为280×435.
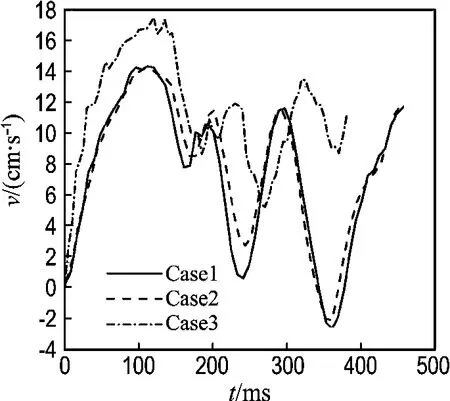
图2 网格对气泡上升速度的影响Fig.2 Effects of mesh on bubble rising velocity
气泡上升过程中其受力主要包括表面张力、浮力和黏性力等,由于平动吹气头的扰动作用,其运动过程与静态流场中的上升过程不同.奥托斯数Eo和莫顿数Mo可以用于描述气泡上升过程的受力过程,并且能够描述气泡的形状变化以及运动特性.

其中Eo表示浮力与表面张力的比值,Mo表示黏性力与表面张力的比值.
图3为初始直径4 mm、平动频率200 r/min的不同时刻的速度矢量图,随着吹气头的平行往复运动其附近会形成较强的搅动流场,吹气头上表面附近出现小的旋涡,初始时刻由于气泡距离吹气头较近,其运动受到附近搅动流场的影响,但其运动方向与吹气头平动方向正好相反,这是吹气头上方的小旋涡造成的;随着气泡的上升,吹气头的搅拌作用对气泡的影响越来越小,熔池上方的流场主要受气泡控制,在气泡周围由于气泡的上升带动液体运动,而气泡上方区域则几近静止.

图3 气泡上升过程形状及速度矢量图Fig.3 Instantaneous bubble shapes and velocity vectors
2.1 初始气泡直径对气泡运动的影响
平动频率为100 r/min时气泡上升轨迹如图4所示(Δt=66.67 ms).可以看出,初始直径为4 mm,即Eo=2.04时,气泡由初始的球形变为椭球形,并且一直保持椭球形,形状变化不明显,没有气泡的破碎.此时作用在气泡上主要的力是表面张力和浮力.气泡受浮力作用向上运动,表面张力使气泡力图维持球形,两个力共同作用使气泡呈椭球形.初始直径为6 mm的气泡,Eo=4.59,也未见气泡破碎,其上升过程中一直保持椭球形.初始直径为8 mm的气泡,Eo=8.16,其上升过程中,初始阶段还保持椭球形,100 ms时变成球帽形,之后又变成椭球形;继续上升则又变成球帽形,并形成非对称尾涡.气泡呈螺旋形上升,到330 ms时已经开始破碎.此时平动流场只在吹气头附近,远离吹气头上方流场受吹气头影响很小,气泡周围流场主要受气泡影响.此时浮力比表面张力大得多,表面张力不足以使其保持球形,使气泡变成球帽形,并最终破碎.
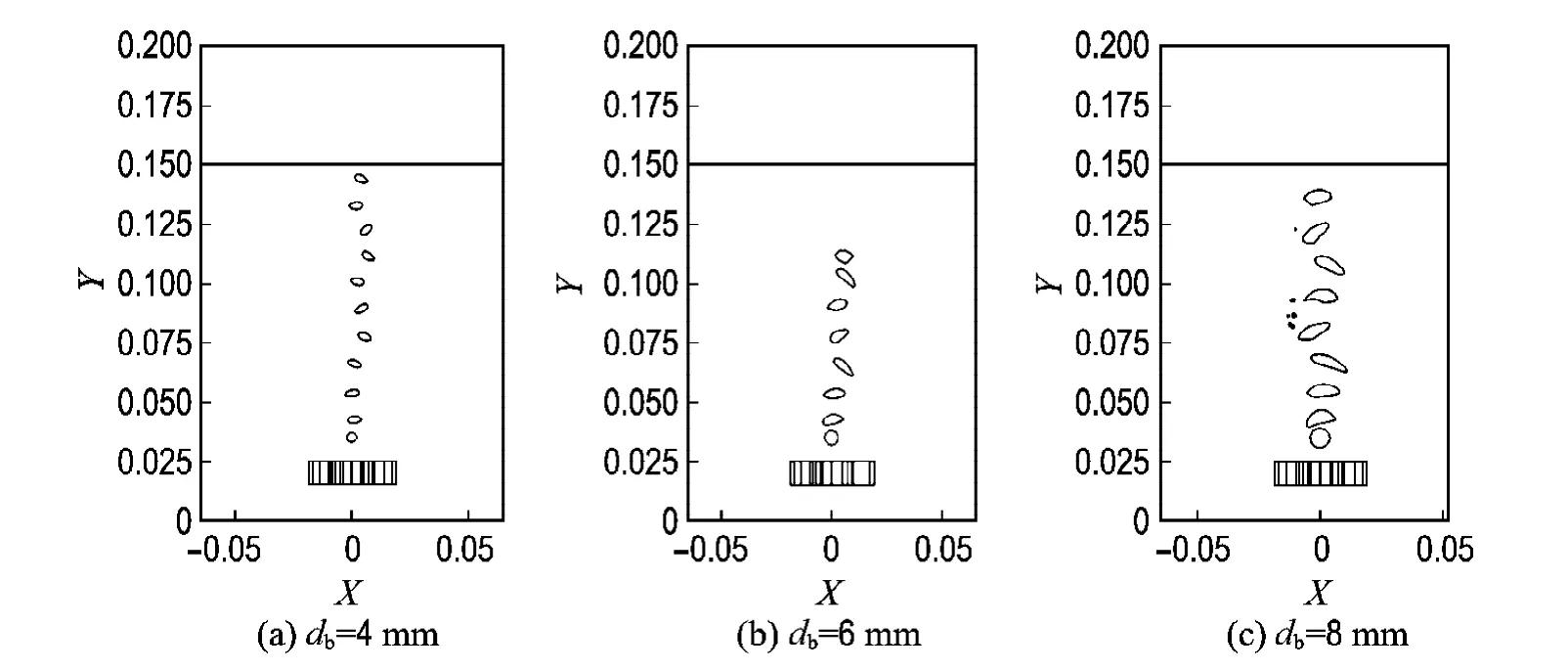
图4 气泡直径对气泡上升轨迹的影响Fig.4 Effects of bubble diameter on bubble rising trajectories
图5为平动频率为100 r/min,不同气泡直径下气泡上升速度的对比,可以看出气泡由初始静止迅速加速,不同直径的气泡均在150 ms左右开始上升,速度变化不大,但有一定波动,从平均值来看,气泡越小,平均终速越大;上升速度的波动程度与气泡直径有关,气泡越大,其波动程度越大,说明气泡螺旋上升趋势越强.

图5 气泡直径对气泡纵向速度的影响Fig.5 Effects of bubble diameter on bubble rising velocity
气泡横向速度受气泡直径影响如图6所示(平动频率100 r/min),可见,气泡水平方向运动速度呈正弦规律变化,随着气泡直径的增大,其振动频率增加而振幅减小,说明气泡越大,其螺旋上升趋势越强.
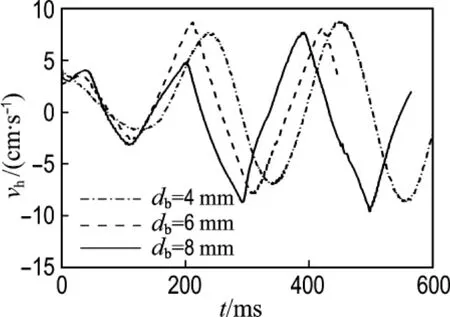
图6 气泡直径对气泡横向速度的影响Fig.6 Effects of bubble diameter on bubble transversal velocity
图7是初始直径为4 mm的气泡上升轨迹,平动频率ω分别为0、100和200 r/min,可以看出,气泡在上升过程中,都是从初始的球形变成椭球形,不同平动频率对气泡形状变化影响不大,但气泡上升过程中运动轨迹却不相同,吹气头不动时气泡上升过程偏离中心线最远,而平动频率为200 r/min时气泡反而会沿中心线垂直上升,说明上升过程中吹气头频率较高的往复运动抑制了气泡的偏移.

图7 平动频率对气泡上升轨迹的影响Fig.7 Effects of reciprocating frequency on bubble rising trajectories
图8为初始直径为4 mm的气泡不同平动频率上升速度的对比,平动频率分别为0、50、100和200 r/min,可以看出,气泡均由初始静止迅速加速,不同平动频率气泡达到平均速度的时间有一定差异,吹气头静止时,气泡达到最大上升速度后又开始减速,并随着时间的推移,上升速度脉动较大,这是由于气泡上升轨迹呈螺旋形(如图5所示).平动频率为50 r/min与静止相似,当平动频率上升到100和200 r/min时,气泡上升速度到达终速后变化不大,但仍有一定波动,说明气泡所受的浮力与流体作用在气泡上的阻力已经基本趋于平衡.从平均值来看,平动频率越大,终速脉动越小.
图9为初始直径为4 mm的气泡不同平动频率横向速度的对比,可以看出,除平动频率为200 r/min外,其他均近似为余弦规律变化,这是由于气泡上升轨迹呈螺旋形.平动频率为200 r/min时气泡水平方向速度接近于0,说明气泡近似于垂直上升.
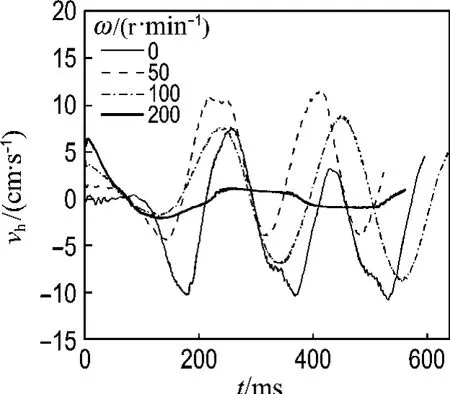
图9 平动频率对气泡横向速度的影响Fig.9 Effects of reciprocating frequency on bubble transversal velocity
2.2 Mo及Eo对气泡运动特性的影响
图10示出Eo对气泡形状的影响(Δt=66.667 ms).气泡直径和表面张力不同,但Eo相同时,气泡的运动特性及破碎规律一致.Eo=4.59时,气泡没有出现破碎现象,其上升过程中形状变化都是从球形变为椭球形,且其长宽比相近,这是因为这两种情况下浮力与表面张力之比相同.而Eo=8.16时,气泡在第330 ms时出现破碎且气泡破碎时间一致.所以确定气泡形状及破碎条件不能只看气泡直径,而应从相似原理出发,找到决定气泡破碎及形状变化的主要参数,即Eo.在本文模拟范围内,Eo=4.59时气泡不会破碎,Eo=8.16时气泡会发生破碎.说明Eo越大,气泡越易破碎.

图10 不同Eo时气泡上升轨迹Fig.10 Bubble rising trajectories at different Eo
Eo及Mo对气泡运动的影响见图11及12.图11给出了气泡横向速度与Eo及Mo的关系,Mo同为9.33×10-11时,Eo不同的两个气泡横向速度相似,Mo最大的气泡其横向速度脉动最小,说明黏性阻力越小,越会促使气泡加速上升.图12给出了气泡纵向速度与Eo及Mo的关系,Mo同为9.33×10-11时,Eo不同的两个气泡初始上升速度基本相同,之后各自在其平均上升速度附近有一定波动.其中Eo大的气泡终速平均值大于Eo小的气泡,这是因为Eo大的气泡所受的浮力更大.4个气泡比较而言,Mo最大的气泡达到终速后其速度波动最小,说明黏性力越大,其上升过程越规则.图12中Eo=8.16,Mo=5.24× 10-10情况下上升速度有突然增大现象,这是因为气泡发生了破碎.
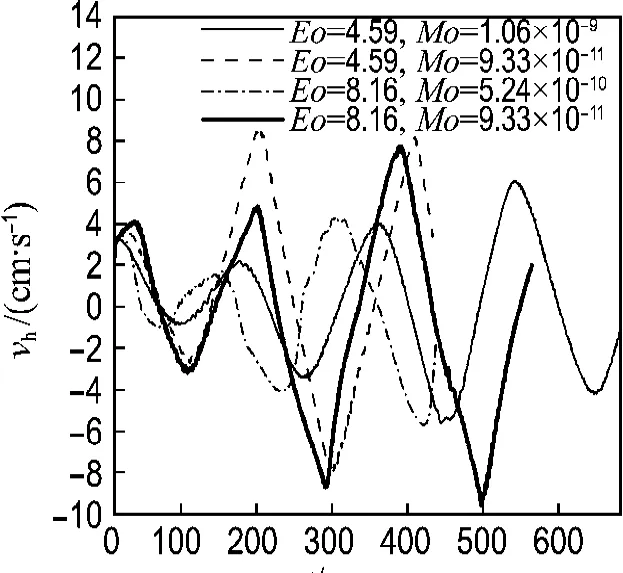
图11 Eo及Mo对气泡横向速度的影响(ω=100 r/min)Fig.11 Effects of Eo and Mo on bubble transversal velocity(ω=100 r/min)
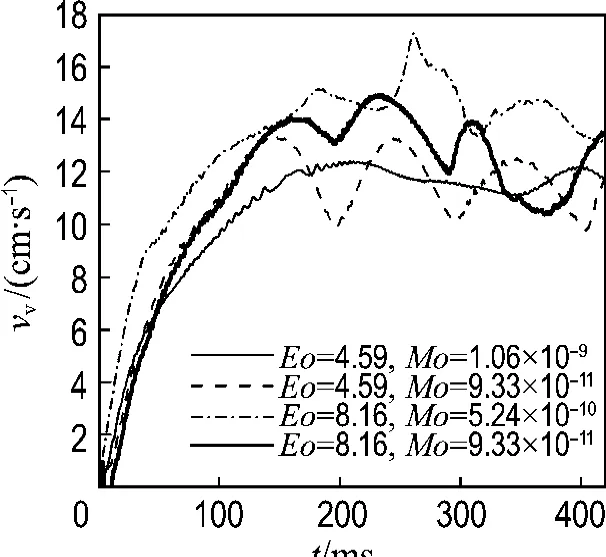
图12 Eo及Mo对气泡纵向速度的影响(ω=100 r/min)Fig.12 Effects of Eo and Mo on bubble rising velocity(ω=100 r/min)
3 结 论
(1)初始静止的气泡在平动吹气头搅动流场中螺旋上升,上升过程中会发生形状变化,气泡越大,形状变化越显著,甚至发生气泡破碎现象.判断气泡形状变化及破碎的标准要视Eo而定,不能单纯以气泡直径为标准,本文模拟条件下,Eo=4.59时气泡不会破碎,Eo=8.16时气泡会发生破碎,说明Eo越大,气泡越易破碎.
(2)气泡上升轨迹与气泡直径、流场平动频率及Mo有关,气泡直径越大,其螺旋上升趋势越强.在分析范围内,平动频率越大,Mo越大,其螺旋上升趋势越弱.定量分析气泡上升规律应以Mo为标准.
[1]GERLACH D,ALLEBORN N,BUWA V,etal.Numerical simulation of periodic bubble formation at a submerged orifice with constant gas flow rate[J].Chemical Engineering Science,2007,62(7):2109-2125
[2]解茂昭,韩 微,刘 红,等.液态金属熔体中气泡运动特性数值模拟[J].大连理工的学学报,2006,46(3):340-344
(XIE Mao-zhao,HAN Wei,LIU Hong,etal.Numerical simulation of single bubble motion behavior in molten metal[J].Journal of Dalian University of Technology,2006,46(3):340-344)
[3]李彦鹏,白博峰.气泡从浸没孔中生成与上升的数值模拟[J].水动力学研究与进展A辑,2006,21(5):660-666
[4]MORUD K E,HJERTAGER B H.LDA measurements and CFD modeling of gas-liquid flow in a stirred vessel[J].Chemical Engineering Science,1996,51(2):233-249
[5]LANE G L,SCHWARZ M P,EVANS G M.Predicting gas-liquid flow in a mechanically stirred tank[J].Applied Mathematical Modeling,2002,26:223-235
[6]HIRT C W,NICHOLS B D.Volume of fluid(VOF)method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39:201-205
[7]LI Yong,ZHANG Jian-ping,FAN Liang-shih.Discrete-phase simulation of single bubble rise behavior at elevated pressures in a bubble column[J].Chemical Engineering Science,2000,55(20):4597-4609
[8]LORSTAD D,FUCHS L.High-order surface tension VOF-model for 3D bubble flows with high density ratio[J].Journal of Computational Physics,2004,200(1):153-176
[9]KRISHNA R,BATEN J M.Rise characteristics of gas bubbles in a 2D rectangular column:VOF simulations vs experiments[J].International Communications in Heat and Mass Transfer,1999,26(7):965-974
[10]BOTHE D,SCHMIDTKE M,WARNECKE H J.VOF-simulation of the rise behavior of single air bubbles in linear shear flows[J].Chemical Engineering &Technology,2006,29(9):1048-1053
[11]宋会玲,解茂昭,刘 红,等.气泡在液态金属搅拌流场中运动与变形的影响因素分析[J].工程热物理学报,2008,29(12):2053-2056

