计入船体变形影响的轴系动态校中研究
石 磊, 薛冬新, 宋希庚
(1.大连理工大学能源与动力学院,辽宁大连 116024;2.上海海事大学商船学院,上海 201306)
0 引 言
船体变形作为影响船舶推进轴系动态校中质量的一种非常重要的动态因素,在轴系动态校中过程中不容忽视[1].因此,计入船体变形影响的轴系动态校中研究具有十分重要的意义.
目前的研究大都将船体视为弹性梁,根据装载状态判断船体弯曲变形方向,且假定最大挠度处发生最大弯矩,再按线性关系计算局部变形[2],这种方法过于简化,计算结果难以保证.文献[3]综合考虑了装载和波浪作用引起的船体变形,但仍然用梁代替船体结构,且将轴线作为考察变形的基准,也不够准确.文献[4]利用船体尾部的三维有限元模型求解船体局部变形,计算结果表明船体模型的建立范围和选用的边界条件对船体变形影响很大.但迄今为止还没有对船体尾部模型提出合理的受力和约束条件,也没有考虑环境温度对轴系动态校中的影响.另外,研究中一般假设轴承处的船体变形即为轴承变位[5],但实际上在波浪荷载的作用下轴系随船体一同纵倾,因而纵倾不应计入轴承变位中,这种假设不够准确.
本文旨在研究计入船体变形影响的轴系动态校中,综合考虑引起船体变形的各种荷载因素的计算和分析方法,提出一种计入船体变形影响、合理转换轴承变位以优化校中的轴系动态校中方法.以76 000 t成品油轮为例,建立整船的有限元模型,计算并施加多种工况下的重力、浮力及环境温度,同时模拟海水弹性支撑作为边界约束,得到各种影响因素作用下的船体变形;并以空船静水状态作为船体变形的基本状态,分别采用多项式和直线拟合船体二层底变形和纵倾,差值求解轴系各轴承的变位以优化校中计算,从而实现考虑船体变形影响的轴系动态校中.
1 模 型
1.1 轴系模型
76 000 t成品油轮推进轴系由曲轴、中间轴和螺旋桨轴连接而成,其校中模型如图1所示.图中:▲表示轴系中各轴承,滑动轴承适用于低速重载工况,抗冲击能力强,径向尺寸小,装拆方便,且寿命长,价格相对便宜,该船轴系全部采用滑动轴承;↓表示集中质量,包括螺旋桨、飞轮及主机各缸曲柄连杆机构的质量;↑表示链轮拉力.

图1 76 000 t成品油轮推进轴系模型Fig.1 Propulsion shafting model of 76 000DWT product oil tanker
1.2 船体有限元模型
应用ANSYS有限元分析软件建立整船的有限元模型,如图2所示.

图2 76 000 t成品油轮有限元模型Fig.2 FE model of 76 000DWT product oil tanker
2 船体变形计算及分析
实践证明,船舶装载状态、波浪荷载及环境温度是引起船体变形的最主要因素[6、7].
2.1 船舶力荷载的研究计算
(1)船舶重力
对76 000 t成品油轮,取两种极限装载状态,即压载到港和满载出港,其余装载状态均介于这二者之间.且由于轴系校中的施工过程是在静水中完成的,将空船静水状态作为衡量其他工况船体变形的基本状态[8].因此,主要考察空船、压载到港和满载出港3种典型装载状态.
(2)船舶浮力
对76 000 t成品油轮,首先进行静水平衡计算,根据邦戎曲线求得船舶在不同装载状态下的静水浮力分布.通常用阶梯形浮力分布代替真实的浮力分布,虽然与实际情况有所差别,但不会给计算带来明显误差[7].
由于坦谷波能够提供船舶遭遇最大波浪的近似波形,采用坦谷波理论描述船舶遭遇波浪[9].通常取计算波长等于船长[7],即76 000 t成品油轮的遭遇波长为220 m.一般以波长的分数形式确定计算波高[7],还有学者建议依据船舶实际航行海区的海浪长期统计资料确定波高,所以取计算波高为2.5 m,它出现频率较高[10].综上,船舶遭遇波浪选定为220 m波长、2.5 m波高的坦谷波,按波峰或波谷位于船体几何中心两种典型位置进行考察.
浮力是由浸水船体形状决定的[11],基于船体型线图和型值表,采用梯形法计算各理论站的横剖面浸水面积,从而得到波浪海况下的浮力分布.需要注意的是,波浪会造成浮力分布的变化,所以需根据装载重力修正浮力分布.
2.2 环境温度荷载的选取
受环境温度影响,船体结构温度分布十分复杂,但认为整体上规律变化.由于海水对温度差具有很强的包容能力,将海水看作恒温热源,处于海水中的船体部分也近似认为处于恒温且与海水等温.冬夏两季水面上下可能存在最大温差,作为极限环境温度进行考察.分别取海水温度为冬季0℃、夏季20℃,为方便计算,将水面上的船体部分近似为处于沿船高或船宽方向线性变化的温度场中.
2.3 船舶约束
用弹簧单元模拟海水对船体的弹性支撑,其约束刚度可以表示为
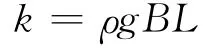
其中ρ为海水密度,g为重力加速度,B和L分别为船宽和船长.为精确计算结果,以理论站为单位修正上式.
另外,为防止船体产生刚体位移,在船体二层底靠近主机自由端选取一组节点,施加纵向和横向约束.
2.4 船体变形计算结果及分析
(1)船舶力荷载作用下的船体变形
船体二层底与轴系相连,二层底的变形直接影响轴系校中状态,因此主要考察船体二层底的局部变形.对76 000 t成品油轮,将上述船舶重力和浮力直接施加在船体有限元模型上,以主机自由端第一轴承作为参照,计算不同力荷载工况下的船体二层底变形d,如图3所示.

图3 力荷载作用下的船体二层底变形Fig.3 Deformations of the double bottom under force loads
由图3可以看出,满载出港时船体二层底变形明显小于压载到港,且船体与波浪的相对位置对二层底变形影响较大.处于压载到港状态的船体在遭遇风浪时二层底变形较大,尤其当波峰位于船中时,船体产生纵倾,二层底变形加剧.
(2)船舶环境温度荷载作用下的船体变形
对76 000 t成品油轮,在各种极限装载状态下取船舶处于静水海况,将上述环境温度荷载施加在船体有限元模型上,仍以主机自由端第一轴承为参照,计算不同环境温差作用下的船体变形.为便于考察环境温度对船体变形的影响,以未计入环境温度影响的船体变形为参考,得到船体二层底相对变形,如图4所示.
由图4可以看出,环境温度对船体二层底变形具有一定影响,二层底的垂向变形主要取决于沿船高方向变化的环境温差,温差越大变形越大.冬夏两季船体二层底变形趋势相反,且满载出港时的船体二层底相对变形明显小于压载到港.
3 计入船体变形的轴系校中
3.1 合理校中
应用有限元法对76 000 t成品油轮推进轴系进行校中计算,以轴承反力为例考察轴系校中状态的变化,计算结果列于表1.

图4 环境温度荷载作用下的船体二层底相对变形Fig.4 Relative deformations of the double bottom under environment temperature loads

表1 轴系合理校中计算结果Tab.1 Rational shafting alignment results
直线校中时,前尾轴承脱空,因而应适当抬高前尾轴承,降低后尾轴承、中间轴承和主机各轴承.又由于中间轴承对前尾轴承和主机1#轴承的负荷影响系数较大,为保证各轴承正常工作,应适当降低中间轴承,大幅降低主机轴承,并且倾斜布置主机各轴承,以减小对中间轴承的影响.
3.2 计入船体变形的轴系校中
3.2.1 船体变形对轴系校中的影响 为考察船体变形对轴系校中的影响,需将船体二层底变形转化为轴承变位.当船体发生变形时,二层底不仅相应变形,而且随船体纵倾,而轴系通过轴承直接安装在二层底上,与二层底同时发生纵倾,因而纵倾值不应计入轴承变位中.基于船体有限元模型模拟计算的船体二层底变形表现为离散的节点变形值,因而采用五阶多项式拟合成连续的变形曲线,因为五阶多项式与其他表达式相比表现出较高的拟合精度.二层底随船体的纵倾采用倾斜直线进行拟合,作为计算轴承变位的基准.拟合曲线与直线在轴承处的差值即为轴承的实际变位.以空船静水工况为基本工况,即可得到轴系各轴承在不同荷载工况下的相对变位值.由于环境温度荷载工况较多,仅在起主导作用的垂向环境温差中选取轴承变位较大的工况加以分析,下同.
将求得的轴承相对变位与轴系合理校中(热态)的轴承变位叠加,重新进行校中计算,以考察船体发生变形时轴系校中状态的变化,计算结果列于表2、3.由计算结果可知,无论是在力荷载还是温度荷载的作用下,当船体发生变形时,轴系中各轴承反力均重新分布,尤其是前尾轴承和中间轴承,受船体变形的影响最大,某些工况前尾轴承甚至脱空,无法正常工作.

表2 计入船体变形影响的轴承反力计算结果(1)Tab.2 Bearing reactions considering ship hull deformations(1) k N

表3 计入船体变形影响的轴承反力计算结果(2)Tab.3 Bearing reactions considering ship hull deformations(2) k N
由表2可见,船舶装载状态对轴系校中影响最大.无论是否遭遇波浪,压载到港时的校中结果明显优于满载出港,这是由于虽然压载到港时船体二层底变形相对较大,但变形数据线性趋势好,因而轴承变位相应较小,对轴系校中的影响不大.船体与波浪的相对位置对轴系校中具有一定影响.当波峰位于船体几何中心时,各轴承反力变化有限;当波谷位于船体几何中心时,各轴承负荷分配发生明显变化,尤其是满载出港工况,前尾轴承脱空,无法正常工作.从表3还可以看出,环境温差对轴系校中状态具有较大影响.当船舶装载状态一定时,冬季环境温差作用下的校中结果明显优于夏季,这是由于冬夏两季环境温度场变化趋势相反,致使夏季的轴承变位小于冬季,反而不利于轴系校中.压载到港工况时,季节环境温差引起的轴系校中状态变化不大;满载出港工况时,夏季环境温差对轴系校中造成的不良影响表现明显,且温差越大轴系校中状态越恶劣.
3.2.2 计入船体变形的轴系动态校中 船体变形会改变轴系原有的校中状态,因而在轴系校中计算阶段就应该充分考虑船体变形这一动态因素.船舶在实际航行时可能同时承受外部力荷载和环境温度荷载作用,取某两种较差工况耦合计算.选取船舶处于满载出港状态、遭遇2.5 m波浪、波谷位于船中这一力荷载工况,同时假设船体处于上甲板为40℃的夏季垂向线性变化的温度场中.计算结果显示,两种荷载同时作用下的船体变形及轴承变位并不是一种荷载单独作用时计算结果的简单叠加,耦合作用结果较两种结果线性叠加安全得多.因此,只要在校中计算时保留一定裕度,就可以保证耦合荷载工况时校中状态仍然正常.
基于这一原则,在考虑船体变形的基础上对76 000 t成品油轮进行轴系动态校中优化计算,结果详见表4、5.当船体发生变形时,由于大多数计算工况下的轴承相对变位均低于轴线,且最低变位出现在中间轴承处,主机轴承自自由端向输出端负向变位逐渐增大,因而平置主机有利于轴系各轴承均匀承力.后尾轴承在满载出港工况下变位值有时高于轴系,造成前尾轴承无法正常工作,所以需要适当降低后尾轴承和中间轴承,大幅降低主机各轴承,以有效避免船体变形的影响.尤其对处于夏季环境温度场中的大装载量船舶,其校中状态相对恶劣,若校中施工在冬季进行很容易增大这种不良影响,所以冬季进行校中施工时可以适当降低后尾轴承或抬高前尾轴承.另外,由于前尾轴承与中间轴承之间的负荷影响系数较大,可以考虑采用“取消前尾轴承,将中间轴承后移”这一措施,不仅有利于轴承反力的合理分布,而且可节约生产成本.

表4 计入船体变形影响的优化后轴承反力计算结果(1)Tab.4 Optimized bearing reactions considering ship hull deformations(1) k N

表5 计入船体变形影响的优化后轴承反力计算结果(2)Tab.5 Optimized bearing reactions considering ship hull deformations(2) k N
4 结 论
针对计入船体变形影响的轴系动态校中问题,提出了一种考虑船舶装载状态、波浪荷载及环境温度的船体变形计算方法.并以76 000 t成品油轮为例,计算了船舶在3种极限装载状态下的重力分布及在7种海况下的浮力分布,讨论了环境温度场的分布情况,作为整船有限元模型的荷载边界条件,同时采用弹簧单元约束船体,得到了船体二层底的局部变形.以船体变形数据为基础,提出了轴承变位的计算方法,分别采用五阶多项式和直线拟合了船体二层底变形和纵倾,将二者在轴承处的差值作为轴承变位应用于轴系校中计算,从而实现了计入船体变形影响的轴系动态校中,为姊妹船及同类船舶的校中计算提供了参考.
轴系校中状态受船舶装载尤其是船体尾部装载状态影响最大,装载量越大轴系校中状态越差.波浪荷载对轴系校中具有一定影响,船体与波浪相对位置的变化会造成轴系各轴承负荷分配的明显变化.环境温度对轴系校中状态具有显著影响,冬夏两季相反趋势环境温度作用下的轴系校中结果差别较大,决不容忽视.因此,在进行轴系校中计算时应合理布置轴系,适当降低后尾轴承和中间轴承,大幅降低并平置主机各轴承,以有效避免船体变形的影响.另外,在校中施工中还应该注意并避免季节性环境温差对校中产生的不利影响.
[1]American Bureau of Shipping.Guidance notes on propulsion shafting alignment[EB/OL].[2008-02-19].http://www.eagle.org/eagleExternalPortal WEB/appmanager/absEagle/absEagleDesktop?_nfpb=true&_pageLabel=abs_eagle_portal_rules_guides_download_page&category=All
[2]耿厚才.船舶轴系动态校中技术研究[D].上海:上海交通大学,2003
[3]MURAWSKI L.Shaft line alignment analysis taking ship construction flexibility and deformations into consideration[J].Marine Structures,2005,18(1):62-84
[4]Nippon Kaiji Kyokai.Guidelines on shafting alignment[EB/OL].[2008-02-19].http://www.classnk.or.jp/hp/Publications/Publications_image/Guidelines_on_Shafting_Alignment.pdf
[5]游加慰.轴系校中计算动态因素的研究[J].武汉造船,1998(2):28-31
[6]周继良,邹鸿钧.船舶轴系校中原理及其应用[M].北京:人民交通出版社,1985
[7]王杰德,杨永谦.船体强度与结构设计[M].北京:国防工业出版社,1995
[8]王西丁,钟 涛,武玉增.船体变形对轴系校中的影响与分析[J].上海造船,2005(2):61-63
[9]李远林.波浪理论及波浪载荷[M].广州:华南理工大学出版社,1994
[10]戴仰山,沈进威,宋竞成.船舶波浪载荷[M].北京:国防工业出版社,2007
[11]吴仁元.船体结构[M].北京:国防工业出版社,1986

