基于模拟退火遗传混合算法的指派问题研究

赵 丽， 冯 毅 ZHAO Li,FENG Yi

（1.兰州交通大学，甘肃 兰州 730070；2.兰州理工大学，甘肃 兰州 730050）

指派问题是物流活动中经常遇到的组合性优化问题，应用十分广泛，因此对其研究较多。在实际物流活动中指派问题通常有平衡与非平衡两种类型，即有n项任务，指派n个人员来分派完成称为平衡指派问题；有n项任务，指派m个人员来分派完成称为非平衡指派问题。近几年来模拟退火算法和遗传算法对指派问题在优化领域得到广泛深入的研究和应用，并得到很好的效果。在此基础上本文研究模拟退火遗传混合算法对指派问题的思路及求解。经实例计算该方法收敛较快，搜索效率较高。

1 指派问题数学模型

为方便研究将平衡与非平衡两种指派问题归纳为如下两种形式研究：

设有n项任务，要派m个人去完成，Cij表示第i个人完成第j项任务要付出的代价，tij表示第i个人完成第j项任务所需时间，则如何分派会使整体效益最好，即用时少费用低。

为建立模型引入0－1变量：

1.1 人数大于或等于工作项目时m≥（）n

1.2 人数小于工作项目时m<（）n

式中b——每人限制的最大工作量

2 指派问题的模拟退火遗传混合算法实现

2.1 模拟退火遗传混合算法思想

Step1：选定初始温度t=t0

利用模拟退火算法的温度控制方法选定较合适的初始温度。如果初始温度选择过高会导致计算时间较长，从而降低计算效率。如果初始温度选择过低又有可能使最终收敛得不到最优解。因此根据 （14）式的条件来确定初始温度t0。

式中 Δfij——任意两个相邻的温度差

Step2：确定初始群体initpop

首先，用实数编码方法对任务数n进行编码且不变；

其次，用实数编码方法对人数m进行编码且可以随机抽取；

最后，利用随机生成法对l!l=m-（）1 个解中随机选取一个解为初始群体initpop。

Step3：构造适应函数f0=fitfun1，ft=fitfun1

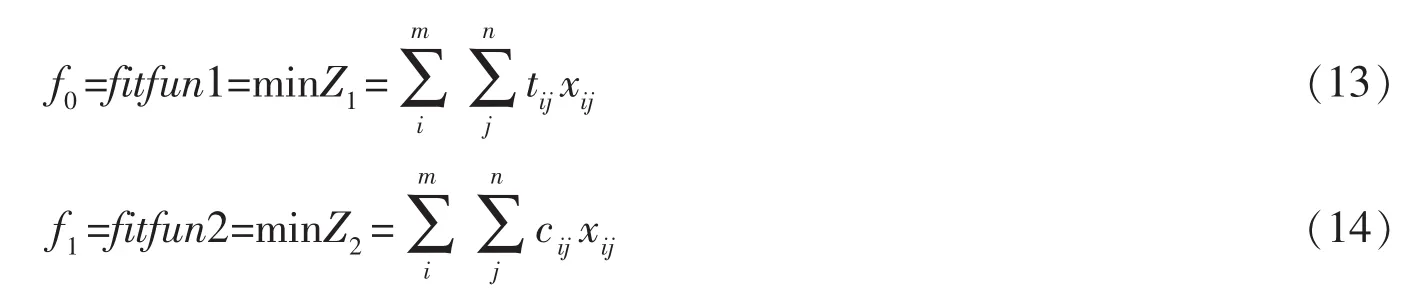
Step4：利用遗传算法对初始群体initpop进行优化，产生种群seedpop1

（1） 确定评价函数eval（ Vi）

（2）利用评价函数可以确定进入种群的个体

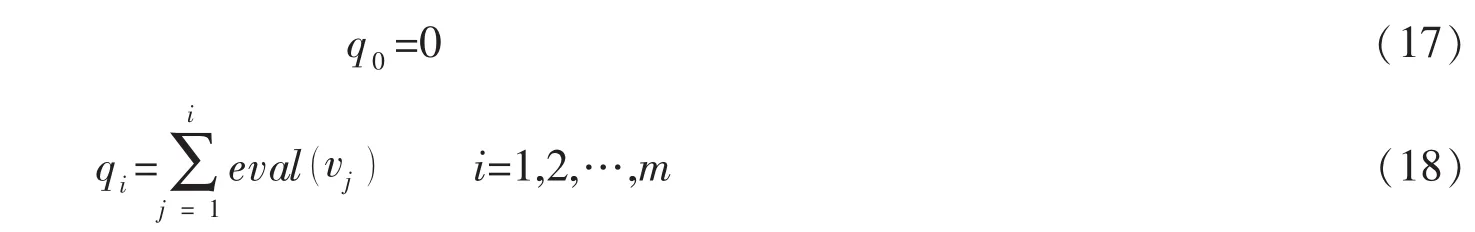
当qi-1≤γ≤qi时 （γ为 （0～1）的伪随机数），第i个染色体进入种群，从而形成种群seedpop1。

Step5：利用模拟退火算法对种群seedpop1进行训练，产生更优的新种群seedpop2

（1）对seedpop1中1～m个体的适应值与初始群体中f0的值进行比较，满足条件的进入seedpop2；

（2）否则，根据评价函数来判断进入seedpop2的个体。当个体的适应值满足时，则选择进入seedpop2；

（3）经过优化训练，产生新种群seedpop2。

Step6：对新种群seedpop2进行交叉、变异，产生子代children

（1）对新种群seedpop2进行双亲双子法交叉，交叉率β，生成crosspop；

（2）再进行变异，交叉率ε，生成mutpop；

（3）生成子代children。

Step7：返回Step4，直到满足终止条件

Step8：得到最优解

3 算例演示

某大型生产企业为生产和人员安全每年都要定期对生产设备进行检修，检修分为平时检修和7月分大检修。现取其中一个车间来做算例，该车间只有3个维修工，平时每次平均会有2个地方出现故障，到7月大检修时该车间5个检修点都要停止运作重新进行检查和修理。已知工人维修故障所需时间Pij见表1，每个维修工的基本维修费用Cij见表2，注：在7月份大检修时天气比较炎热为保证维修工安全要求每个工人至多维修两个故障点。

表1 完成任务所需时间 单位：小时

表2 完成任务所付费用 单位：百元

混合算法相关参数选择α、初始时间t0=6、交叉率β＝0.2、变异率＝0.05。利用前面设计的混合算法进行运算得到结果及比较结果见表3，运行次数都为10次。按照该方案进行分配所得到的完成任务的花费时间大约要比单一使用模拟退火或遗传算法获得最优解短五分之二。

4 结 论

本文结合模拟退火算法和遗传算法的优点，提出模拟退火遗传混合算法来解决实际中的指派问题。指派问题属于组合优化问题，很适合用本文研究的算法来实现。这种混合算法能够准确快速地求解最优结果或分配方案，针对较大规模的指派问题，能够缩短搜索时间，取得良好的效果。

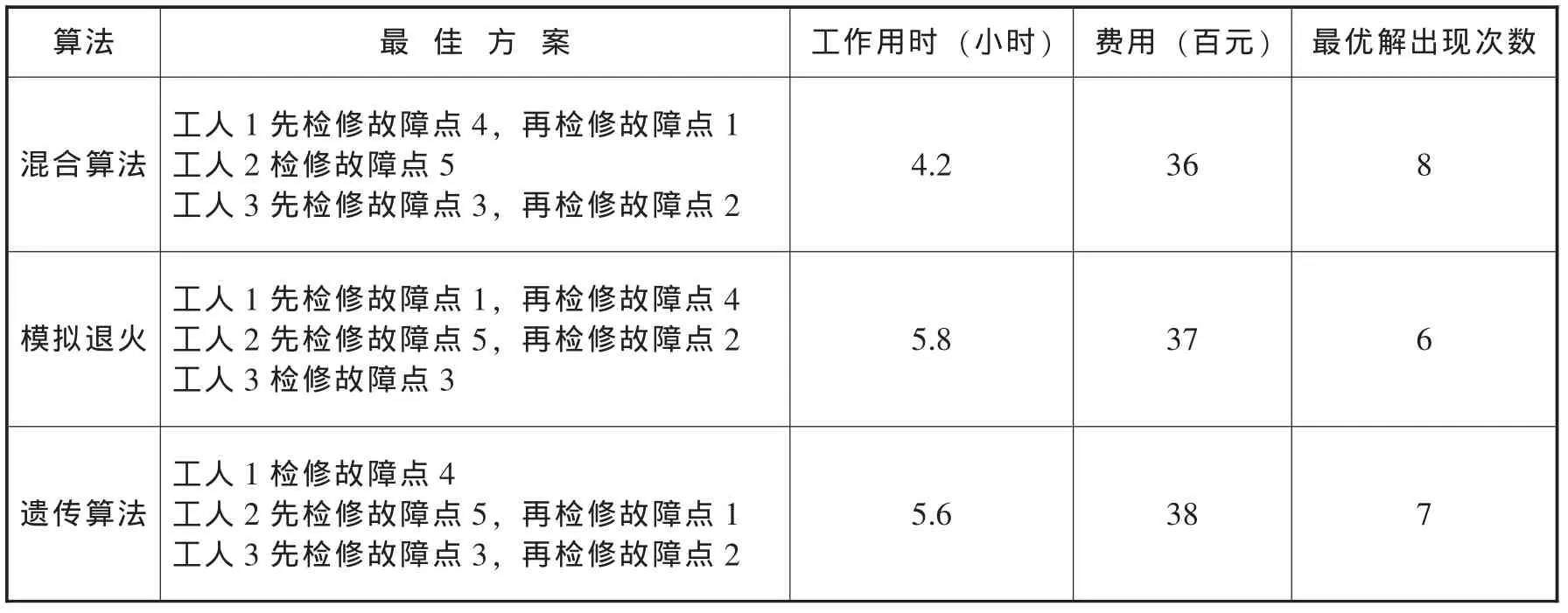
表3

[1] 贺国先.现代物流系统仿真[M].北京：中国铁道出版社，2008.

[2] 焦永兰.管理运筹学[M].北京：中国铁道出版社，2000.

[3] 邢文训，谢金星.现代优化计算方法[M].北京：清华大学出版社，2005.

[4] 谢凡荣.求解指派问题的一个算法[J].运筹与管理，2004(6):24-26.

[5] 张新辉.任务数多于人数的指派问题[J].运筹与管理，1997(3):15-18.

[6] Cattrysse D G,Van Wassenhove L N.A survey of algoirths for the generalized assignment problem[J].Europena Joumla of Operationla Research,1992,60(3):260-272.

[7] Marco Dorigo,Vittorio Maniezzo,Alberto Colomi.Ant system:Optimization by a colony of cooperating agents[J].IEEE Transactions on Cybernetics,1996(26):55-57.