借助四面体巧解异面直线所成的角

●方志平 (惠州市第一中学 广东惠州 516007)

借助四面体巧解异面直线所成的角

●方志平 (惠州市第一中学 广东惠州 516007)

用几何的方法求异面直线所成的角，往往是先通过平移异面直线到相交位置，再找出异面直线所成的角，然后由三角知识求出异面直线所成角的函数值或求出角的大小．由于四面体的任何一组对棱都是异面直线，因此以四面体为载体，把异面直线放在四面体的对棱所在的位置，利用四面体对棱的夹角公式可巧解异面直线所成的角．现阐述如下:

图1

1 四面体对棱的夹角公式

如图1，在四面体A-BCD中，若AC与BD所成的角为90°，则

2 夹角公式的应用

例1在正四面体的侧面三角形的高线中，其“垂足”不在同一侧面上的任意2条所成角的余弦值是 ( )

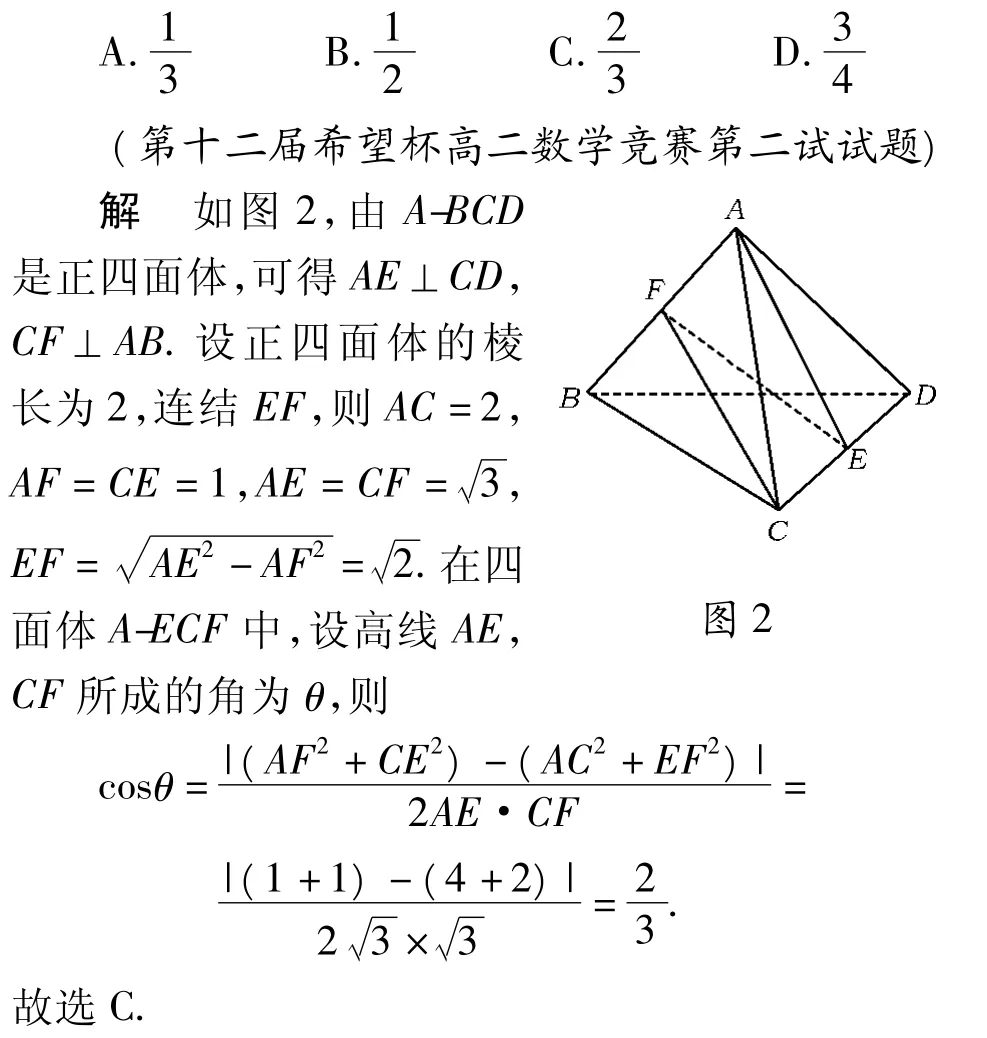
评注本题求解的关键是要把AE，CF放在一个棱长都易求的四面体的一组对棱上，不难发现连结EF，得AECF正是我们寻找的一个四面体．

评注虽然图3中的CA1与C1B是正三棱柱2个侧面的对角线，但连结A1B后，CA1和C1B却是四面体A1BC1C的一组对棱，且四面体A1BC1C所有棱长均可求，故用四面体对棱的夹角公式可求异面直线CA1与C1B所成角的大小．

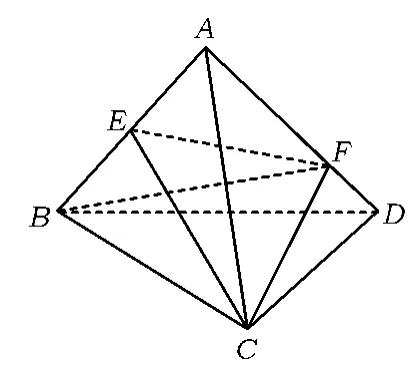
图4

(2008年福建省福州市第30届高中数学竞赛试题)

解如图4，连结 EF，CF．设正四面体 ABCD棱长为6，在△AEF中，

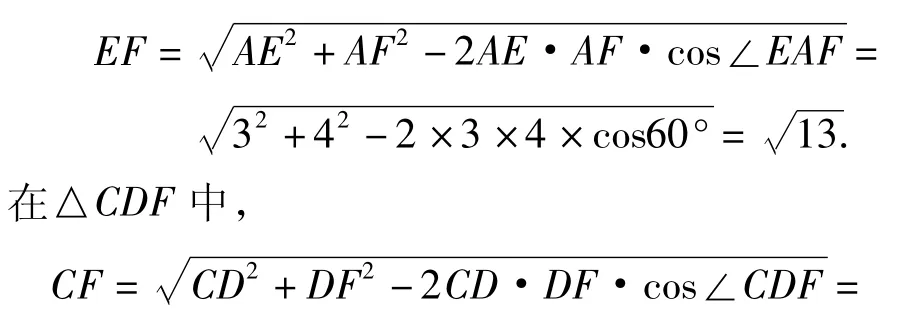
评注本题求解的关键是要构造一个使得CE与BF成为四面体的一组对棱，且该四面体所有棱均可求．显然连结EF，CF可得一个四面体BCFE符合要求，然后借助四面体对棱的夹角公式可求异面直线CE与BF所成角的余弦值，进而求出该角的正弦值．

综上所述，对于任何一对异面直线，以四面体为载体，只要能恰当地把这对异面直线放在一个四面体的一组对棱的位置，且该四面体所有棱长均可求，这样就能巧解这对异面直线所成角的问题．