宁波市高中青年数学教师“说题”大赛试题评析
●张振继 (宁波万里国际学校 浙江宁波 315040)
宁波市高中青年数学教师“说题”大赛试题评析
●张振继 (宁波万里国际学校 浙江宁波 315040)
2010年10月26日,浙江省宁波市举行城区高中青年数学教师“说题”比赛,此种形式的比赛在宁波历史上还是第一次.本文就“说题”中的几道试题进行评析,供教学时参考.
本次活动共分3组,每组4人,一共有12人参加,第1~4人说第1题,第5~8人说第2题,第9~12人说第3题.每人给出思考准备时间15分钟,“说题”时间15分钟.以下笔者逐题进行分析.
题1 设{an}是由正数组成的等比数列,Sn是其前n项和,证明:
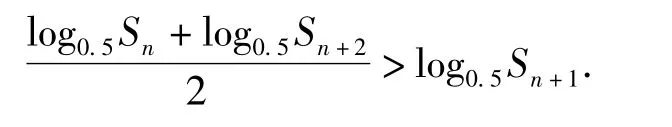
(1995年全国数学高考文科试题)
命题立意本题考查等比数列的前n项和公式、对数函数的单调性及不等式的证明方法,属于中等难度的题目.


本题还可以用数学归纳法(探究),这里略.
题目点评在利用等比数列前n项和公式求解时,应注意对公比q进行分类讨论.但如果利用和数列{Sn}之间的递推关系,那么便可回避分类讨论,优化解题过程.
一般地,在等比数列{an}中,前n项和为

成立,并证明你的结论.
(1995年全国数学高考理科试题)
题2设二次函数f(x)=ax2-2x-2a(a∈R,a≠0),若集合A={x|f(x)>0},集合 B={x|1<x<3},满足A∩B≠φ,求a的取值范围.
命题立意本题考查二次函数、不等式的解集、集合语言之间的转换,属于难题.
思路分析直接利用A∩B≠φ,或从反面入手求解.
解法探究若通过求不等式f(x)>0的解集来求解,由于含有参数,则讨论起来比较复杂.
解法1(直接法)由A∩B≠φ,得存在x∈(1,3),使得 f(x) >0有解(解集非空).
(1)当a>0时,结合二次函数的图像得
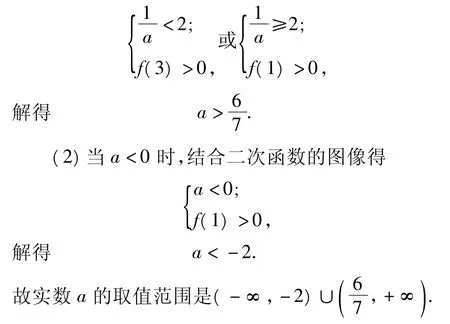
解法2(间接法)由 A∩B=φ,得当x∈(1,3)时,不等式f(x)≤0恒成立.

题目点评本题通过解不等式f(x)>0的解集求解,计算量大而复杂,难度较大.若充分利用数形结合思想,则可以化难为易;另外利用补集思想处理,比较理想,值得回味与深思.
相关链接:
1.已知集合 A={x|-8≤x≤6},B={x|x≤m},若 A∪B≠B,且 A∩B≠φ,则 m 的取值范围是__.
(2005年全国“希望杯”邀请赛高一试题)
2.设函数f(x)=ax2-2x+2 对任意x∈(1,4)都有f(x)>0成立,求实数a的取值范围.
题3已知直线l是圆x2+y2=1的一条切线,它与抛物线y=x2-4交于点A,B,P为抛物线的顶点,求△PAB重心G的纵坐标的取值范围.
命题立意本题考查直线与圆相切、直线与抛物线相交的基础知识,以及数形结合思想、方程函数思想.
思路分析设出点A,B的坐标,将重心G的纵坐标表示为点A,B横(纵)坐标的函数,然后通过求最值解决.
解法探究 解法1设直线l的方程为y=kx+b(k不存在时不符合题意).因为l是圆x2+y2=1的一条切线,所以
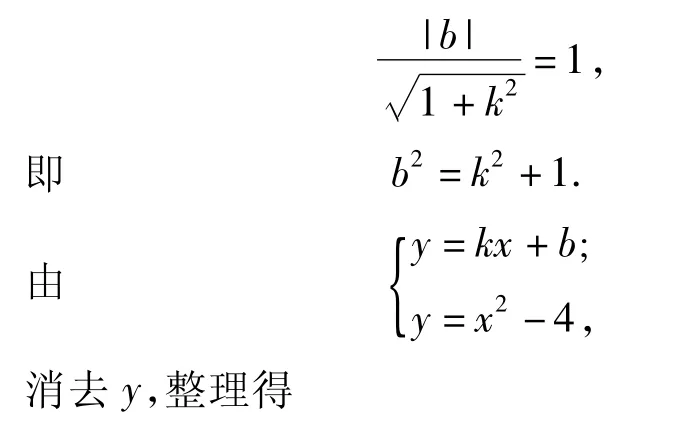


下仿照解法1解之,这里略.
题目点评本题入手容易,关键是进行函数建模,即将重心G的纵坐标表示为点A,B横(纵)坐标的函数,然后利用直线与圆相切、直线与抛物线相交、联立方程组等知识加以解决.
相关链接:
已知点A(0,2)和抛物线y2=x+4上2个点B,C,使得AB⊥BC,求点C的纵坐标的取值范围.
(2002年全国数学联合竞赛试题)

