正弦定理、余弦定理在立体几何中的推广

●常国良 (泰兴中学 江苏泰兴 225400)

正弦定理、余弦定理在立体几何中的推广

●常国良 (泰兴中学 江苏泰兴 225400)

数学命题的推广是数学发展不可缺少的手段，是一项富有挑战性和创新性的活动．近几年的高考试题也加强了对这方面的考查，给考生耳目一新之感．本文给出正弦定理和余弦定理在立体几何中的推广，供参考．

1 在三棱柱中的推广

图1

如图1所示，设三棱柱ABC-A1B1C1的侧面ABB1A1的面积为 S1，侧面 ACC1A1的面积为 S2，侧面 BCC1B1的面积为S3，二面角A-CC1-B，C-BB1-A，B-AA1-C 的大小分别为 α，β，γ，面 A0B0C0为三棱柱的一个直截面．

推广1在三棱柱ABC-A1B1C1中，有

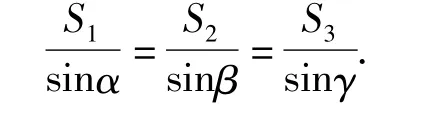
2 在三棱锥中的推广

推广3在三棱锥中，各侧面的面积与其所对棱长的积同该侧棱所在二面角正弦的比都相等．

如图 2所示，在三棱锥 P-ABC中，PA=a，PB=b，PC=c，S△PBC=S1，S△PCA=S2，S△PAB=S3，二面角 C-PA-B，A-PB-C，B-PC-A的大小分别为 θ1，θ2，θ3，则

证明过点P作PO⊥面ABC，PD⊥AB，点O，D为垂足，连结OD．由三垂线定理的逆定理，知OD⊥AB，因此∠PDO为二面角P-AB-C的平面角，即∠PDO= θ，于是

图2

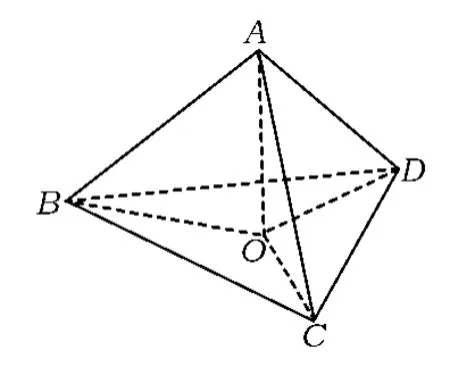
图3

推论在对棱分别相等的三棱锥中，侧棱与其所对二面角的正弦的比相等．

推广4在三棱锥中，它的任意一个面的面积的平方，等于其他3个面的面积的平方和，减去这3个面中每个面的面积与它们所夹二面角余弦积的和的2倍．

如图3，在四面体 A-BCD 中，设顶点 A，B，C，D所对面的面积分别为 S1，S2，S3，S4，其中每 2 个面所夹的二面角分别为 αij(i，j=1，2，3，4，i≠j)，则