平面宏微驱动系统微动台的刚度计算

刘定强 黄玉美 谢 礼 杨 勇

西安理工大学，西安，710048

平面宏微驱动系统微动台的刚度计算

刘定强 黄玉美 谢 礼 杨 勇

西安理工大学，西安，710048

针对宏微进给系统，利用弹性铰的微变形原理设计了宏微系统中的微动台。采用最小位能原理推导出一般弹性铰的二维刚度矩阵；并将此刚度矩阵应用于设计有弹性铰的微进给平台中，给出了所设计的微动台简化的计算模型。将简化模型计算结果与有限元计算结果和实验结果比较，结果证明了该方法的有效性和实用性。

弹性铰；微动台；刚度矩阵；最小位能原理

0 引言

目前，宏微驱动系统在超精密加工中的应用越来越广泛，对其大行程方面的研究尤为必要。在20世纪80年代的中后期，国内外学者相继提出了宏微双重驱动微操作系统的初步想法［1－2］。经过近20年的探索，宏微双重驱动微操作系统目前已是实现高精度定位的一种有效手段［3－6］。因为微动进给平台最大行程也只有几十微米，在实际加工中受到限制。因此在超精密加工中迫切需要能解决大行程问题，而且具有宏微可以协调进给的系统。另外，在大中型精密、超精密加工机床中，工作台一般为大尺度，承受三维空间的全载荷（即有三个方向力载荷和三个方向力矩载荷），且全载荷为较大的载荷。微动台在驱动方向的刚度大小，关系到微动台的位移精度和进给跟踪响应速度。而微动台在驱动方向的刚度又由弹性铰的刚度及其在结构中的布置方式决定。国内外学者对单个弹性铰的研究较多［7－9］，如1965年PAROS等就推导出弹性铰的设计计算公式，并给出了弹性铰厚度远小于其切割半径时的简化计算公式，避免了费时的数值积分，给弹性铰的设计计算带来了极大的方便。由于简化计算公式是在弹性铰厚度远小于半径的条件下给出的，所以在设计较厚的铰链时会有较大的误差。为了提高分析精度，在有限元建模时，常采用三维实体单元进行网格划分，且网格划分较细。但是网格划分过细，会造成含有弹性铰机构的单元数量很大（常常超过几十万），使得分析效率很低，网格划分过粗，又不能得到高的分析精度。建立弹性铰单元刚度矩阵可以大大简化计算［10］。有基于此，本文研究了任意截面弹性铰的平面刚度矩阵，并用最小位能原理推导出弹性铰的二维刚度矩阵，使其可以计算含有任意放置弹性铰链的机构在二维任何方向上的刚度。

1 宏微工作台原理

本文设计的宏微直线运动工作台如图1所示。当压电驱动器产生微量位移时，微动台会在弹性铰链变形的约束下，向y方向移动微量位移。微动台所受6个载荷中，一个为驱动方向的载荷，另外5个为导轨副承受的约束方向的载荷。弹性铰链可以对压电驱动器相对微动台的运动进行导向，同时可以分担微动台部分约束载荷，减小微动台的运动偏差。

1.1 弹性铰的结构

弹性铰结构如图2a所示，其杆部的截面是矩形。本文采用如图2b所示的弹性铰链元件，其原理如图2c所示。

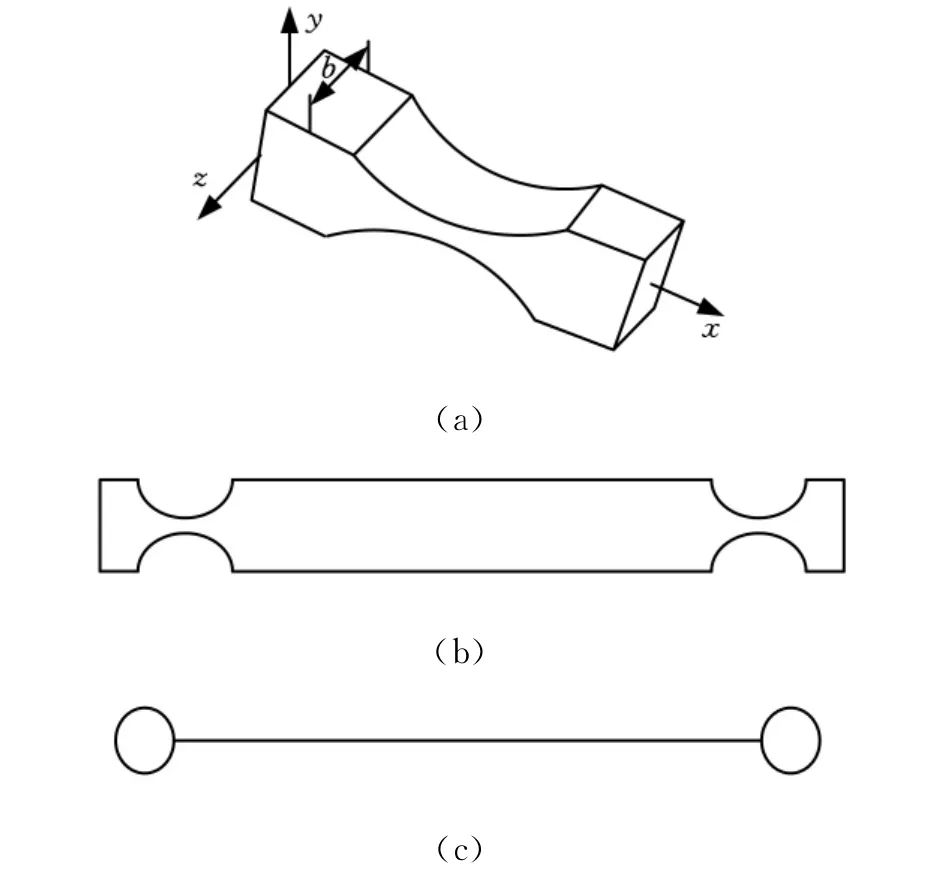
图2 弹性铰元件结构原理图

1.2 微动台设计

微驱动器要通过弹性铰机构把力和位移等输出给微进给平台。该机构的设计是整个微驱动系统设计中的一项关键的工作，弹性铰机构的精确性、合理性和有效性在很大程度上决定了微进给系统的性能参数。

由多个弹性铰元件组成的微动台整体结构，既要兼顾在进给方向微驱动器预紧力的需要，又要能承受横向力和力矩满足微致动器导向的需要。若弹性铰链刚度过高，将影响微驱动器的有效行程和在驱动方向上的承载能力。反之，若刚度过低则承受横向力和力矩能力差，进而导向精度低。本文设计的微动台如图3所示。微动台的进给和四组弹性铰链的变形一起出现，驱动方向为图3中的y方向。同时四组弹性铰链关于微动台对称布置，用于承载横向（x向）约束力和绕z轴的约束力矩。

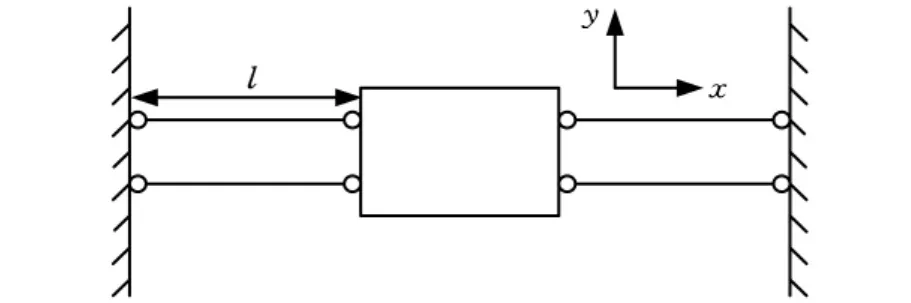
图3 微进给平台机构

2 弹性铰刚度矩阵

2.1 不考虑剪切影响的刚度矩阵

图2a为弹性铰的几何结构，根据文献［4－6，10］的研究，将弹性铰简化成变截面梁的假设是合理的。现用最小位能原理建立单元刚度矩阵，其弹性体的变形位能为

2.2 考虑剪切影响的刚度矩阵

3 微进给平台的简化模型

图4所示为设计的微进给平台的计算模型，因图中的弹性铰为圆弧弹性铰。所以有

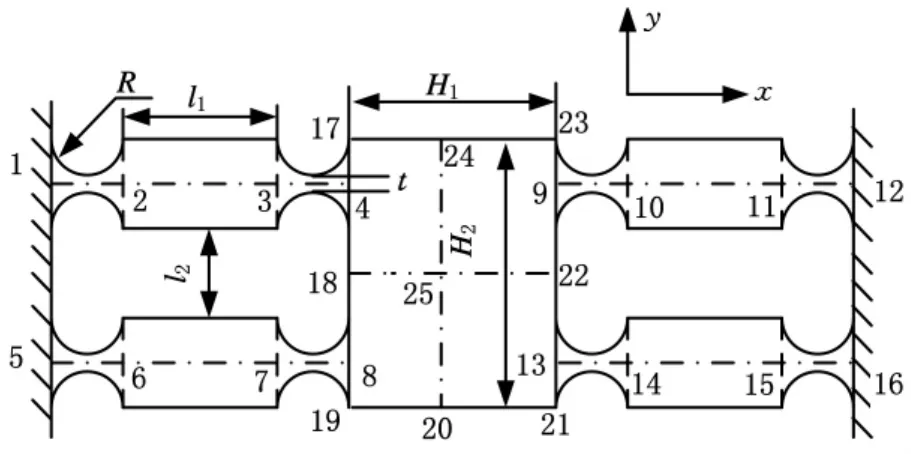
图4 微进给平台的简化模型示意图

图4中标出的数字1～25为划分的单元节点。节点1和节点2之间，节点3和节点4之间是弹性铰单元。节点2和节点3之间是梁单元。节点17、4、18、25和24构成了平面5节点矩形单元。同理，节点5和节点6，节点7和节点8，节点9和节点10，节点11和节点12，节点13和节点14，节点15和节点16分别构成弹性铰单元。节点6和节点7，节点10和节点11，节点14和节点15构成梁单元。节点24、25、22、9和23为平面5节点矩形单元。节点18、8、19、20和25为平面5节点矩形单元。同样，节点25、20、21、13和22也为平面5节点矩形单元。这里要解决弹性铰单元和平面5节点矩形单元之间的连接问题。节点17和节点18的位移矩阵为

在以节点3和节点4之间的弹性铰构成的单元中，节点4的位移矩阵为

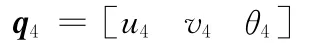
在以节点17、4、18、25和24构成的平面5节点矩形单元中，节点4的位移矩阵为

显然，节点4的位移矩阵不能完全对应。由于节点17、18、4之间存在梁的悬臂连接关系，因此可建立约束关系：

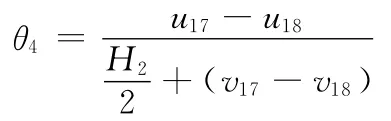
从结构上看，只要在所组装的整体刚度方程中考虑了上述约束关系，就可以实现弹性铰单元和平面5节点矩形单元的连接。

4 数值计算与实验

图4所示微进给平台的结构，参数分别为：弹性模量E＝206GPa，泊松比μ＝0.3，R＝5mm，t＝2mm，b＝32mm，l1＝10mm，l2＝30mm，H1＝30mm，H2＝54mm。计算结果如表1所示。表1中的ANSYS解，是用划分的33 759个节点、26 710个单元而计算的三维实体结果。kx、ky、kθz分别为微动工作台x方向刚度、y方向刚度和绕z轴的转动刚度。表1中第二行最后一列括号中的24.8700，是用文献［3-4］推导的计算公式计算的结果，22.4500则是实验测试的结果。刚度实验测试装置如图5所示，图中左边和中间各安装有一个直式电感测微仪，测量精度为0.1μm；右边安装的是LCM500压力传感器；左边安装的测微仪是为了测量出微动工作台在受力时的整体移动。当右边加外力后，中间的直式电感测微仪的读数减去左边直式电感测微仪的读数，即为微动平台的变形位移ε。右边压力传感器的读数除以ε就为微动平台y方向的刚度。实验结果和本文方法的计算结果接近。

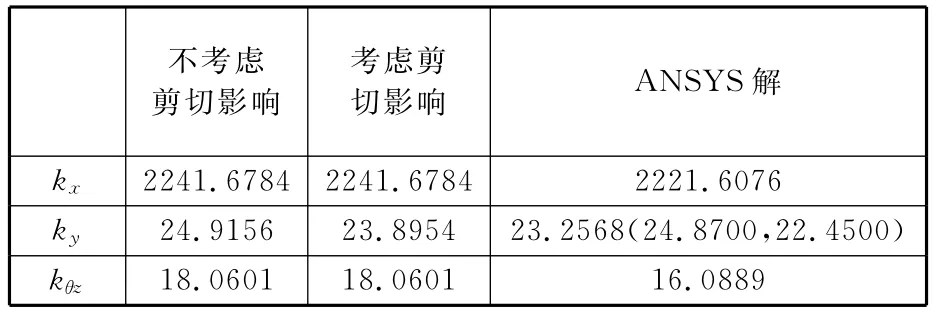
表1 四对弹性铰链工作平台刚度的计算结果 N／μm

因为用有限元方法计算的结构偏硬，所以从表1可以看出，几个计算结果比实验结果刚度大。当弹性铰链简化成变截面梁，且长宽比较小时，考虑剪切对结果的影响是比较可取的。因为考虑剪切的计算结果更加接近实验结果。

由于本文对系统作了25个节点、16个单元的离散，比用ANSYS直接进行实体单元离散的节点和单元数少得多，在计算结果与实验结果一致的前提下，计算效率高很多。

图5 现场实验测试

5 结论

（1）本文推导了已知截面形状函数的弹性铰的刚度矩阵。用本文方法计算的结果及实体有限元计算结果，以及实验结果有很好的一致性。因为离散节点单元数少，使计算时间大为缩短。

（2）长宽比较小时，考虑剪切影响比不考虑剪切影响能获得更好的精度。研究结果为微动工作平台的优化设计以及对整体机械系统的分析有很好的帮助。

［1］ Sharon A，Hogan N，Hardt D E.High Bandwidth Force Regulation and Inertia Reduction Using a Macro／Micro Manipulatior System［C］／／The 1988 IEEE International Conference on Robotics ＆ Automation，Philadephia，1988，126－132.

［2］ Weber T E，Hollis R L.A Vision Based Correlator to Actively Damp Vibrations of a Coarse－fine Manipulator［C］／／The 1988IEEE International Conference on Robotics ＆ Automation，Scollsdale，1989，818－825.

［3］ Chen O J，Wolfgang H.Development of 4DOF Planar Macro－micro Manipulators System［C］／／The IEEE 28th Annual Conference on Industrial Electronics，Sevilla，2002，2231－2236.

［4］ Chung S J，W K，Youm Y.On the Coarse／Fine Dual－Stage Manipulators with Robust Perturbation Compensator［C］／／The 2001IEEE International Conference on Robotics ＆ Automation.Seoul，2001，121－126.

［5］ Elfizy A T，Bone G M，Elbestawi M A.Design and Control of a Dual－stage Feed Drive［J］.International Journal of Machine Tools ＆ Manufacture，2005，45：153－165.

［6］ Chu Chihliang，Fan Shenghao.A Novel Long－travel Pizeoelectric－driven Linear Nanopositioning Stage［J］.Precision Engineering，2006，30：85－95.

［7］ Paros J M，Weisboro L.How to Design Flexure Hinge［J］.Machine Design，1965，37（27）：151－157.

［8］ Jung Seungbae.Improvement of Scanning Accuracy of PZT Piezoelectric Actuators by Feed－forward Model－reference Control［J］.Precision Engineering，1994，14：49－55.

［9］ Dona F D E，Munteanu M G H.Optimized Flexure Hinge for Compliant Micromechanisms［J］.Analog Integrated Circuits and Signal Processing，2005，44：163－174.

［10］ 杨国兴，张宪民，王华.基于有限元方法的柔性铰链式微夹持器优化设计［J］.中国机械工程，2006，17（10）：1074－1078.

Stiffness Calculation of Micro－feed Table in Macro－micro Dual Drive Plane Load

Liu Dingqiang Huang Yumei Xie Li Yang Yong
Xian University of Technology，Xian，710048

For the system of macro micro－feed table，a micro－feed table in macro－micro dual system was designed by using of flexure hinge.The 2Dstiffness matrix was derived from principle of minimum potential.And the stiffness matrix was applied to micro－feed table which contained flexure hinges.A simplified computation model of the micro－feed table was obtained.The results of simplified model were compared with finite element model and laboratory results.The effectiveness and practicality of the method were tested and verified.

flexure hinge；micro－feed table；stiffness matrix；principle of minimum potential

TH703

1004—132X（2011）01—0088—04

2010—03—08

国家自然科学基金资助项目（50875209）；国家重点基础研究发展计划（973计划）资助项目（2009CB724406）

（编辑 何成根）

刘定强，男，1980年生。西安理工大学机械与精密仪器工程学院博士研究生。研究方向为精密数控装备。黄玉美，女，1941年生。西安理工大学机械与精密仪器学院教授、博士研究生导师。谢 礼，男，1983年生。西安理工大学机械与精密仪器工程学院硕士研究生。杨 勇，男，1983年生。西安理工大学机械与精密仪器学院硕士研究生。