自增强超高压容器残余应力分析
袁格侠 刘宏昭 范彩霞,3 王娟平 王 胜
1.西安理工大学,西安,710048 2.宝鸡文理学院,宝鸡,721007 3.焦作大学,焦作,454150
自增强超高压容器残余应力分析
袁格侠1,2刘宏昭1范彩霞1,3王娟平2王 胜1
1.西安理工大学,西安,710048 2.宝鸡文理学院,宝鸡,721007 3.焦作大学,焦作,454150
为分析自增强超高压容器的残余应力,利用ANSYS的APDL语言开发了筒形超高压容器的参数化有限元模型,利用该模型并采用多载荷步法对容器自增强处理的加载过程和卸载过程进行了仿真。通过改变端部边界条件和材料参数研究了容器端部形式和材料参数对容器残余应力的影响。研究结果表明:端部形式对容器中部的周向应力和径向应力影响很小,对轴向应力影响较大,使轴向应力在内壁附近有较大的差别;切线模量不同,最大周向残余应力所在位置不同,大的卸载切线模量可以增大内壁处的周向残余应力。在ANSYS的BKIN材料模型下定义两种温度应力-应变曲线以分别模拟材料加载和卸载时的机械性能,准确地模拟了这类材料的应变硬化和鲍辛格效应,提高了残余应力预测的精度。
超高压容器;残余应力;自增强;双线性材料;参数化
0 引言
缩套与自增强技术通常用于超高压容器,使容器内壁产生周向残余压应力,以提高容器的弹性承载能力并延长疲劳寿命。缩套技术使容器材料来源广泛,可以满足不同的工作环境,但最大残余应力却受到过盈量的限制[1-2]。文献[1-2]分别对不同金属材料制成的多层容器和硬质合金内衬的多层容器的优化设计进行了深入研究。
自增强技术可以提高容器内壁附近的抗疲劳能力,而内壁残余压应力的增大却受到材料鲍辛格效应(bauschinger effect,BE)的影响。材料自增强残余应力的计算准确与否直接影响到自增强容器弹性承载能力及疲劳强度等的设计计算[3]。自增强残余应力的计算主要集中在对材料力学模型的建立。模型中对材料鲍辛格效应和应变硬化行为的考虑与否是准确计算厚壁圆筒自增强残余应力的关键。Hill[4]首先提出了基于材料理想弹塑性假设的自增强理论模型。但由于未考虑上述两个因素,使得使用理想弹塑性模型计算的残余应力和实际残余应力之间有较大的差别。因此,研究人员先后提出了一些分别考虑材料的鲍辛格效应和应变硬化行为的自增强理论模型。近年来出现了同时考虑应变硬化行为和鲍辛格效应的自增强理论模型[3,5-8],这些模型给出了比理想弹塑性模型更精确的结果。
文献[9-11]基于ANSYS对具体筒体自增强处理进行了有限元仿真,材料选用BKIN模型,准确模拟了材料加载时的应变硬化,但没有准确模拟卸载时的鲍辛格效应和应变硬化。文献[12]利用ANSYS软件对一个具体的自增强高压食品装置进行了疲劳寿命计算。
本文在ANSYS大型分析软件下,利用其二次开发语言APDL建立了超高压容器参数化有限元模型。采用米赛斯(M ises)屈服准则,使用多载荷步分析方法,对容器的自增强处理进行仿真。该仿真方法可用于自增强超高压容器的初步设计,减少模拟管的数量,节约设计成本。
1 超高压容器参数化有限元模型
1.1 材料的力学模型
厚壁圆筒自增强残余应力分析的最大难点在于材料模型的准确描述。大多数用于承受高压或超高压的筒壁材料在拉伸时表现出理想弹塑性或线性应变硬化,压缩时为线性硬化或幂硬化特性。从图1所示的应力-应变曲线可以看出该类材料具有明显的鲍辛格效应。卸载幂硬化材料可近似拟合成线性硬化材料来研究。此时拉/压应力应变曲线变成双线性模型,可以用4个斜率来表示材料的应力应变特性。
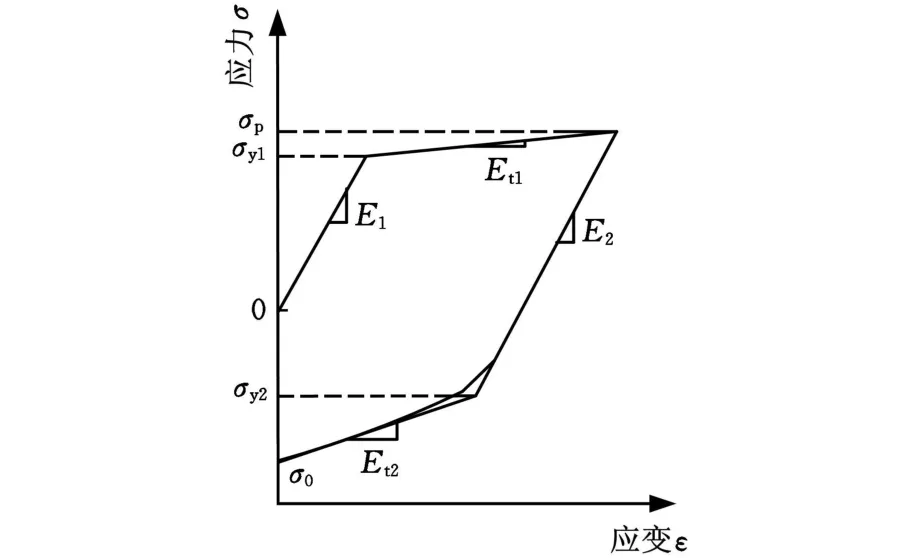
图1 实际材料模型与双线性材料模型对比
图1中,E1为加载弹性模量,E t1为加载切线模量,σy1为加载屈服极限,σp为加载时的峰值应力,E2为卸载弹性模量,Et2为卸载切线模量,σy2为卸载屈服极限,σ0为卸载时应变为零时的应力值。当最大塑性拉应变不同时,σp和 σy2有着不同的值,初始塑性拉应变愈大,鲍辛格效应愈强。
ANSYS材料模型中没有双线性力学模型,但其提供了双线性随动硬化模型BK IN,见图2。并且该模型还提供了温度相关特性,可以在不同温度下定义多条应力应变曲线,且可以和TBOPT选项一起使用,设置成随着温度的增高无应力松弛。利用这一功能,可以在两个温度 T1、T2下定义两条应力曲线,T1用于模拟材料的加载性能,T2用于模拟材料的卸载性能,这样可以简单方便地正确模拟图1所示的双线性材料的应变硬化和鲍辛格效应。BKIN模型T2下的屈服极限σy2由加载时的屈服应力和峰值应力以及反向屈服应力来决定。
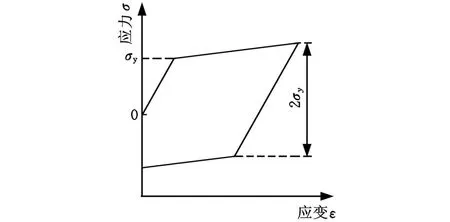
图2 BKIN材料模型
1.2 参数化容器分析模型的建立
为便于对不同几何尺寸、不同材料属性的自增强容器进行残余应力分析,建立容器的参数化模型,并自动完成网格划分和分析是十分必要的。
容器的几何模型为圆筒周向的1/4,将其内径、外径及长度进行参数化,通过多行用户提示对话框输入。单元类型选用3D Solid45或Solid95。材料模型为上述提到的BK IN模型,其8个机械性能也进行了参数化。
由于网格划分的疏密对分析结果有较大的影响,因此对网格划分进行参数化也十分必要,这样用户可根据容器尺寸的大小及精度要求控制网格的划分。厚壁圆筒是规则图形,适合采用映射划分。本文采用控制线段的份数来控制网格的疏密。划分网格后的有限元模型见图3,共有10(周向)×50(径向)×5(轴向)=2500个单元。
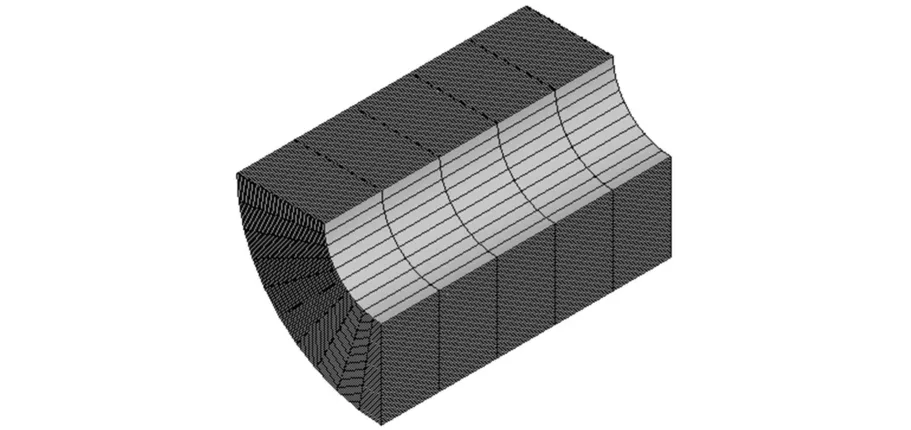
图3 厚壁圆筒有限元模型
2 超高压容器自增强ANSYS仿真
采用ANSYS多载荷步分析方法进行仿真,第一步,在 T1温度下进行内壁加载应力分析;第二步,在T2温度下进行卸载分析。
假定一厚壁圆筒径比(外径与内径之比)K=2.5,材料泊松比μ=0.3,材料的其他性能参数为σy1=900MPa,E1=209GPa,E t1=10GPa,E2=200GPa,E t2=20GPa,σ0=-600MPa 。
2.1 端部形式对残余应力的影响
厚壁超高压容器的端部形式有三种,即开式圆筒(平面应力状态)、闭式圆筒(拟平面应变状态)和两端固定式圆筒(平面应变状态)。后两者的径向应力和周向应力分布基本相同,都按平面应变来处理。在自增强压力p a=800MPa时,这两类容器的轴向、径向和周向残余应力见图4~图9。图4~图9中显示:在平面应变状态下,整个容器的轴向上,沿径向的应力分布是相同的;对于开式容器,两端部的应力分布沿中间横截面对称;对于细长形筒体,如高压炮管、高压压缩缸,除两端部外,中间大部分应力分布相同。

图4 平面应变状态径向应力
图5 平面应变状态周向应力
如图10所示,开式容器的端部和中部应力分布不同,轴向应力在内壁处差别最大,周向应力在内壁与外壁处也有较大的差别,而径向应力在内外壁附近差别较小,在中间处差别较大。对于两端固定式和闭式筒体,其径向和周向应力与开式筒体的中间部分基本相同,而轴向应力在内外壁附近有着较大的差别。
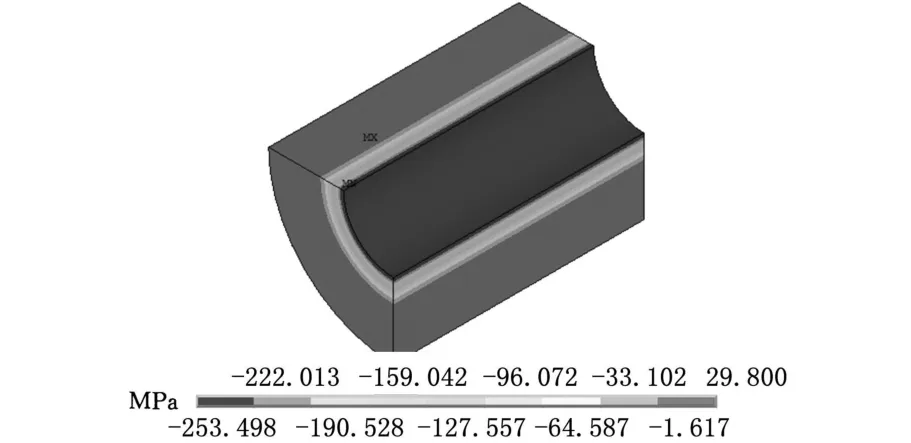
图6 平面应变状态轴向应力
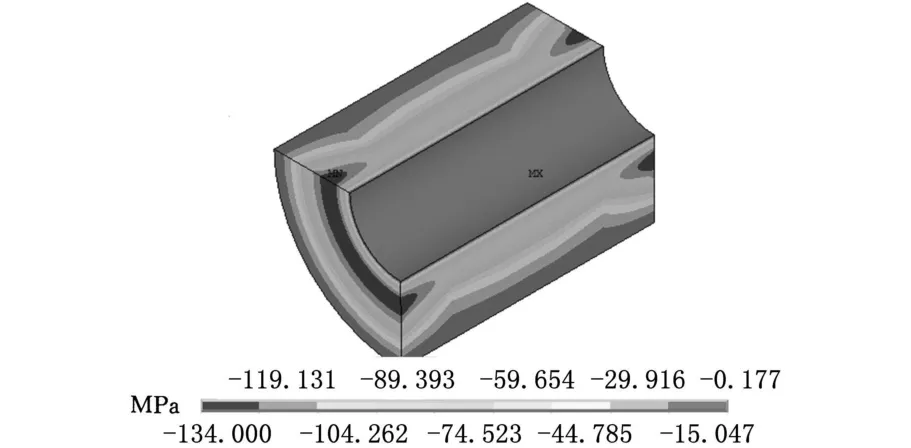
图7 开式容器径向应力
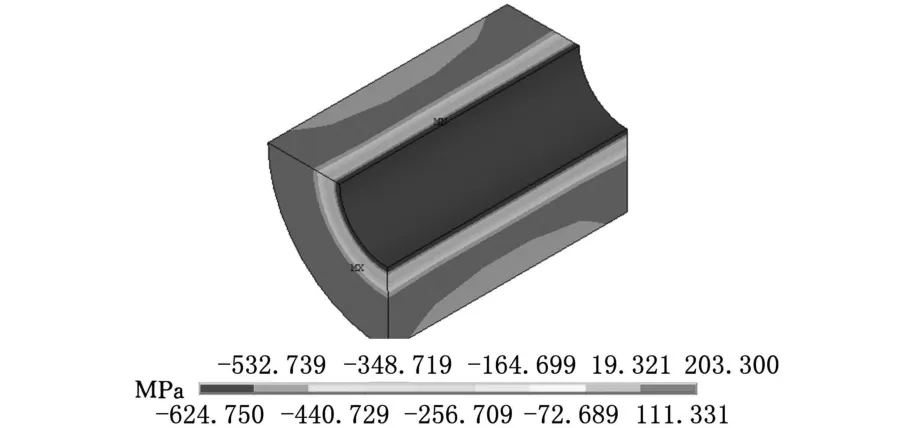
图8 开式容器周向应力

图9 开式容器轴向应力

图10 残余应力分布比较曲线图
2.2 材料参数对残余应力的影响
不同的材料有着不同的拉/压应力应变曲线,即使是同种材料,由于热处理状态的不同,其拉/压应力应变曲线也有着很大的差异。对于超高压容器用钢,其拉伸阶段基本为理想弹塑性,硬化程度很小,即E t1很小。在E t1及卸载屈服极限σy2不变的情况下,材料反向加压时的应变硬化度Et2对残余应力的影响见图11。
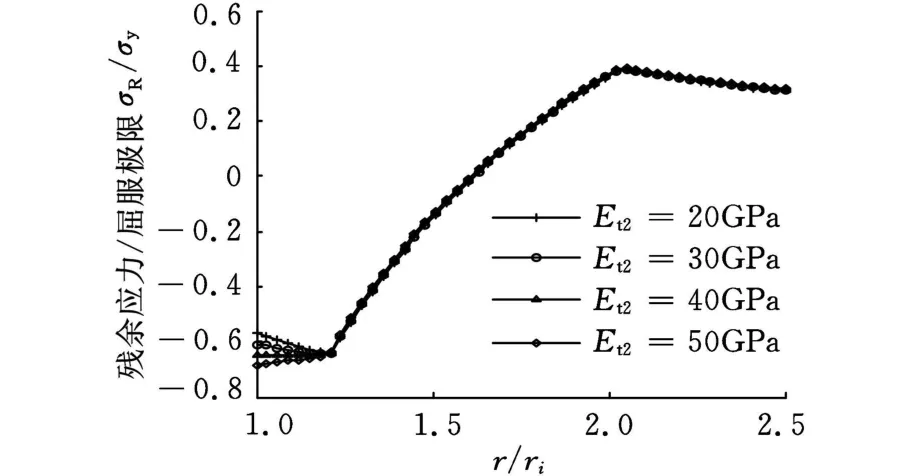
图11 E t2对残余应力的影响
图11显示,E t2只对反向屈服区的应力产生影响。当Et2大时,自增强筒最大残余应力在内壁处,而当E t2小时,反向屈服部分的残余压应力也随之变小,筒壁的最大残余压应力也由内壁移动到反向屈服处。若E t2小,自增强处理时不允许发生反向屈服,否则,容器内壁处得不到最大残余压应力,若Et2大于某一数值时,虽有反向屈服发生,但还可进一步提高内壁处的残余应力。
3 有限元模型的验证
3.1 仿真结果与解析解的比较
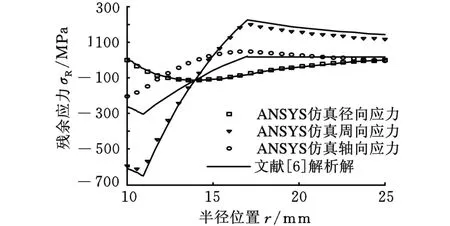
图12 开式容器仿真与文献[6]残余应力比较
文献[6]在轴向应变为常数且假定材料不可压缩的情况下,对材料的真实拉/压应力应变曲线进行二次曲线拟合,给出了自增强管残余应力的解析解。容器几何参数和材料参数与本文第2节中所述相同。自增强压力为851.4MPa时,开式容器ANSYS仿真中部结果与文献[6]计算结果见图12。从图12中可以看出,径向应力和周向应力的误差很小,轴向应力有较大的差别。对于开式容器自增强加载过程,沿径向的轴向应变并非常数,ANSYS仿真结果从内径到外径为0.365 94×10-3到 -0.663 23×10-3,文献[6]计算结果为常数-0.8597×10-3;卸载过程ANSYS仿真结果为-0.4611×10-3到-0.4761×10-3,近似为常数,文献[6]计算结果为 -0.6365×10-3,且文献[6]假设开式容器沿轴向应力分布相同。在平面应变状态下,径向、周向和轴向残余应力仿真与计算结果都很一致。
3.2 实验验证
Huang等[3]在平面应力状态下(即开式筒体)和假定材料不可压缩的情况下,考虑鲍辛格效应和屈服准则的影响,给出了自增强管残余应力的解析解,并进行了实验,根据实验结果,调整屈服应力系数,使之计算结果接近实测结果。其解析解的计算结果为超高压容器的中部残余应力值,不能对高压炮管等开式圆筒端部残余应力进行较精确的计算。本文应用文献[3]中的实验数据对该模型进行验证。实验筒体几何参数为内径19.3mm,外径 43.7mm;材料参数为 σy1=960.7MPa,σp-σy2=1420GPa,E1=207GPa,E2=201GPa,Et1=7026MPa[3]。通过对材料拉/压曲线(图 13)DE段的线性拟合,得 E t2=76 760MPa。网格划分为10(周向)×122(径向)×10(轴向)。自增强压力pa=740MPa,按开式筒体进行仿真,容器长度为160mm。
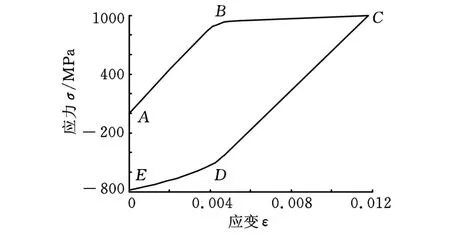
图13 材料拉/压应力应变曲线[3]
实际容器进行自增强处理时,必须在自增强压力下进行一段时间的保压,使其筒体在该压力下达到充分的塑性变形。仿真时,内壁加压后,在内压作用下,容器内孔变大,当达到平衡时,其压力值减小。因此为了仿真时更接近工程实际,先加压740MPa,分析完后查看内壁压力,中部为726.8M Pa,端部为731.72MPa;再增加压力值到750MPa,中部为 736.82MPa,端部为741.904MPa。在施压740MPa和750MPa下,残余应力分布与实测值及文献[3]的计算值如图14所示,其中,σe为有效应力。
从图14中可看出,对卸载进行线性拟合后,仿真结果除在屈服半径处误差稍大外,其余残余应力和实测值一致。施压750MPa时的预测结果略优于Huang(未调整屈服应力)的计算值,而施压740MPa时其内壁的残余应力预测值误差也在5%之内,其预测结果也略优于 Parker的数值解[3]。Huang等通过实验对屈服应力进行调整后,其弹性区的计算结果更接近实测值。

图14 仿真与Huang等[3]实验残余应力比较
比较和实验验证说明本文的模型与仿真方法是正确的,预测结果是可靠的。
4 结论
(1)使用有限元软件ANSYS的APDL语言建立了高压容器自增强残余应力计算参数化模型,可对不同几何尺寸、不同材料属性的容器进行自动建模和分析,便于工程应用。并将模型的仿真值与文献[6]和文献[3]的解析解、Paker的数值解[3]及Huang等的实验值[3]进行了对比,证明了模型计算结果的可靠性。
(2)通过在BKIN材料模型中定义两种温度的应力-应变曲线,准确模拟了双线性材料力学模型,提高了残余应力预测的精度。
(3)研究了端部形式对残余应力的影响。研究结果表明,细长形开式和闭式容器除端部外,其余部分径向和周向残余应力的分布基本与两端固定式相同。
(4)研究了材料参数对残余应力的影响。卸载应变硬化系数E t2对反向屈服部分的残余应力分布有很大的影响:E t2大,则靠近内壁处的残余应力大;Et2小,则靠近内壁处的残余应力小。随着E t2的减小,筒壁的最大残余压应力也由内壁移动到反向屈服处,为容器自增强处理时是否可发生反向屈服提供了判断依据。
[1] Yuan Gexia,Liu Hongzhao,W ang Zhongm in.Optimum Design for Shrink-fit Mu lti-layer Vessels under Ultrahigh Pressure Using Different M aterials[J].Chinese Journal of Mechanical Engineering,2010,23(5):582-589.
[2] 袁格侠,刘宏昭,王忠明.硬质合金内衬的组合超高压筒体优化设计[J].工程力学,2011,28(1):212-218.
[3] Huang X P,CuiW C.Effect of Bauschinger Effect and Yield Criterion on Residual Stress Distribution of Autofrettaged Tube[J].ASME J.Pressure Vessel Technology,2006,128:212-216.
[4] H ill R.The M athematical Theory of Plasticity[M].New York:Oxford University Press,1950.
[5] Darijani H,Kargarnovin M H,Naghdabadi R.Design of Thick-walled Cylind rical Vessels under Internal Pressure Based on Elasto-plastic Approach[J].M aterials and Design,2009,30(9):3537-3544.
[6] H osseinian E,Farrahi G H,Movahhedy M R.An Analytical Framew ork for the Solution of Autofrettaged Tubes Under Constant Axial Strain Condition[J].ASM E J.Pressure Vessel Techno logy,2009,131(6):061201-1-8.
[7] Farrahi G H,H osseinian E,Assempour A.General Variable Material Property Formulation for the Solution of Autofrettaged Thick-Walled Tubes W ith Constant Axial Strains[J].ASM E J.Pressure Vessel Technology,2008,130(4):041209-1-7.
[8] Parker A P.Autofrettage o f Open-end Tubespressures,Stresses,Strains and Code Comparisons[J].ASM E J.Pressure Vessel Technology,2001,123(3):271-281.
[9] 姜学艳.GYF300型超高压水晶釜筒体自增强处理有限元仿真与残余应力分析[D].呼和浩特:内蒙古工业大学,2007.
[10] 姜学艳,刘慧颖,吉仁塔布.超高压厚壁圆筒自增强处理有限元仿真与残余应力分析[J].化工装备技术,2010,36(1):14-17.
[11] 贾红光.基于ANSYS的厚壁圆筒的弹塑性应力分析[J].青海大学学报(自然科学版),2010,28(3):8-12.
[12] Alegre JM,Bravo P,Preciado M.Fatigue Behavior of an Autofrettaged H igh-p ressure Vessel for the Food Industry[J].Engineering Failure Analysis,2007,14(2):396-407.
Analysis of Residual Stress for Autofrettaged U ltrahigh Pressure Vessels
Yuan Gexia1,2Liu Hongzhao1Fan Caixia1,3Wang Juanping2Wang Sheng1
1.Xi'an University of Technology,Xi'an,710048
2.Baoji University of A rts and Sciences,Baoji,Shannxi,721007
3.Jiaozuo University,Jiaozuo,Henan,454150
To analyze residual stress of autofrettaged pressure vessels,APDL language of ANSYS was used tom odel its param etric FE,which was used to emu lated the loading and unloading of autofrettaged pressure vessels by usingmultiple load step of ANSYS.Effects ofend conditionsof the vesselandm aterial parameters on the residual stress w ere studied.The results show that end conditions have few effectson hoop residual stressand radial residual stress,and have bigger effectson axial residual stress in near the bore;the location of the greatest hoop stress depends on un loading tangent modulus,big unloading tangentm odulus can improve the residual stress of near the bore.The studies used ANSYSBKIN(bilinear kinematic hardening)m odel to simulate loading and unloading ofmaterialm echanical p roperties by defining two temperature p rofiles for thematerial,and im prove the prediction precision of the residual stress.
ultrahigh pressure vessel;residual stress;autofrettage;bilinearmaterial;parameterization
TH 49
1004—132X(2011)05—0536—05
2010—07—23
陕西省教育厅专项科研计划项目(2010JK 397);宝鸡市2010年科技计划工业攻关项目;宝鸡文理学院重点科研项目(ZK 0727);陕西省重点学科建设专项资金资助项目
(编辑 袁兴玲)
袁格侠,女,1970年生。西安理工大学机械与精密仪器工程学院博士研究生,宝鸡文理学院机电工程系副教授。主要研究方向为高压容器的强度与失效分析、机电系统建模与仿真。发表论文 10余篇。刘宏昭,男,1954年生。西安理工大学机械与精密仪器工程学院教授、博士研究生导师。范彩霞,女,1976年生。西安理工大学机械与精密仪器工程学院博士研究生,焦作大学机电工程学院讲师。王娟平,女,1976年生。宝鸡文理学院机电工程系讲师。王 胜,男,1974年生。西安理工大学机械与精密仪器工程学院博士研究生。

