考虑失效相关的盾构机刀盘驱动多级行星传动系统的可靠性模型
赵 勇 秦大同 武文辉
1.重庆大学机械传动国家重点实验室,重庆,400044
2.中信重型机械公司,洛阳,471039
考虑失效相关的盾构机刀盘驱动多级行星传动系统的可靠性模型
赵 勇1秦大同1武文辉2
1.重庆大学机械传动国家重点实验室,重庆,400044
2.中信重型机械公司,洛阳,471039
考虑到行星齿轮传动系统中各齿轮存在多种模式的失效,且各失效模式间又存在着多种因素的相关性,根据应力-强度干涉理论,提出了在多失效模式及多因素相关条件下机械传动系统可靠性的一般计算模型。应用该模型对盾构机刀盘驱动多级行星传动系统进行了可靠性分析。首先建立了齿轮、轴承等各失效单元的可靠性模型,然后考虑系统中主要发生失效的模式及各失效模式间关于载荷和使用系数的相关性,建立了传动系统的可靠性模型,并用Monte-Carlo法对模型计算结果进行仿真验证,结果表明,该模型可以准确地评估盾构机刀盘驱动多级行星传动系统的可靠性。
行星齿轮传动;应力-强度干涉理论;系统可靠性;多模式失效相关
0 引言
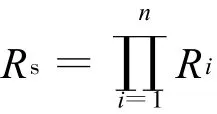
在考虑相关性的系统可靠性研究方面,Ditlevsen[7]通过考虑两两失效模式之间相关性的影响,提出了二阶可靠度区间估计方法。Ang等[8]提出概率网络估算技术(PNET法),将其用于结构体系失效概率点的估计计算。Rackwitz等[9]提出降维法,近似计算结构系统失效概率。李云贵等[10]采用条件概率和数值计算技术,提出了结构体系失效概率估算的近似数值分析方法。成刚虎等[11]推导了在中高可靠度和低可靠度两种情况下考虑失效相关性的可靠度求解模型。康海贵等[12]提出了采用改进的等价平面法,并将其用于计算串联体系或并列体系的失效概率。上述分析方法的共同之处,在于不可避免地涉及失效模式间相关系数的求解,而相关系数的计算具有一定的经验性,没有明确的物理意义,并可能会使计算结果与实际可靠度之间存在较大差异[13]。文献[14-18]运用应力-强度干涉模型,建立考虑各失效模式关于单一因素—载荷相关的机械传动系统的可靠性模型。由于积分运算复杂,故具体应用时也只针对单一轮齿或一对齿轮的两种失效模式间的相关性来进行。对于考虑在多失效模式及多因素相关条件下的复杂机械传动系统的可靠性模型的研究和应用,国内外尚不多见。
本文基于应力-强度干涉原理,建立了在多失效模式及多因素相关条件下的复杂机械传动系统可靠性的一般计算模型,并将该模型应用于盾构机刀盘驱动主减速器多级行星传动系统中,准确计算了该传动系统的可靠度。计算结果表明,所建模型可以较为准确地反映该行星传动系统的可靠性。
1 系统可靠性分析
由于盾构机刀盘的工作转速低(1.3r/min左右)、输出扭矩大(480kN◦m左右),刀盘驱动主减速器结构上通常采用三级2K-H行星传动串联的形式,其机构如图1所示。其中,si表示第i级的太阳轮,pi表示第i级的行星轮,ri表示第i级的内齿轮,i=1,2,3,g1~g3表示各级的行星轮轴承。
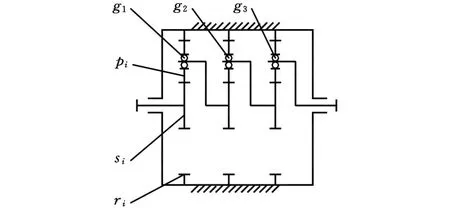
图1 刀盘驱动主减速器机构简图
首先进行FMEA分析,确定主减速器传动系统中的重要元件及其主要失效形式。将系统各元素按影响系统可靠性的程度分为A、B、C三类。划分结果如表1所示。计算传动系统可靠性时主要考虑A类元素的影响。对B类、C类元素,由于它们与传动性能相关性不大,影响较小,或有些零件的可靠度为1,因此在计算时暂不考虑[19]。另外,A类元素中的输入输出轴、各级行星架、行星轮轴和花键连接的可靠性一般都很高,可认为十分可靠,计算时可不考虑。因此,整个行星齿轮传动系统的可靠性可认为是由各级太阳轮、行星轮、内齿轮和各级行星轮轴承组成的串联系统的可靠性所决定的。
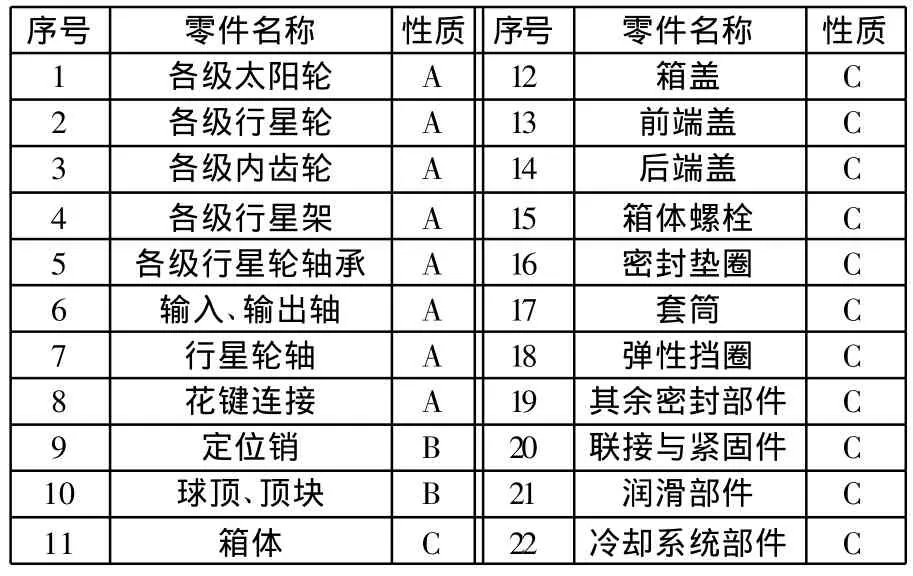
表1 主减速器传动系统元素的分类
对于一般的闭式齿轮传动,齿轮的主要失效模式有两种,即齿面接触疲劳破坏和齿根弯曲疲劳破坏,轴承的失效形式主要是疲劳点蚀破坏。因此,对行星齿轮传动系统的可靠性分析主要针对这3种失效形式来进行。具体分析时,根据上述3种失效形式,将行星传动系统的失效分解成由各个齿轮和轴承组成的多种失效单元的串联组合。盾构机刀盘驱动主减速器的任意一级均为2K-H型行星传动系统,第i级的太阳轮和内齿轮均有两种失效单元,分别是太阳轮的接触失效单元和弯曲失效单元以及内齿轮的接触失效单元和弯曲失效单元,简记为 H(si)、F(si)、H(ri)、F(ri);行星轮则有4种失效单元,分别是与太阳轮啮合的接触疲劳单元和弯曲疲劳单元以及与内齿轮啮合的接触疲劳单元和弯曲疲劳单元,简记为 H(psi)、F(psi)、H(pri)、F(pri)。轴承的疲劳点蚀失效单元记为H(gi)。若该级行星传动中行星轮的个数为n p,行星轮4种失效单元的任意一种实际上均由n p个失效事件在功能上串联构成,即n p个失效事件任意一个的发生都会影响系统的正常运转,而不能简单认为是结构上的并联关系[20-21]。又由于这n p个失效事件中任两个事件都是相等的,由概率论的知识,n p个失效事件便可以等效为其中的任意一个失效事件。同样,太阳轮或内齿轮的任意一种失效模式实际上也是由n p个失效事件在功能上串联构成的,由于各事件之间完全相关,因此只按一种失效模式来处理。各级行星轮轴承的失效也是完全相关的,因此,也按一种失效模式来处理。因此,盾构机刀盘驱动主减速器三级行星传动系统的可靠性如图2所示。可见,该行星传动系统是由27个失效单元组成的串联系统,包括24个齿轮失效单元和3个轴承失效单元。

图2 盾构机刀盘驱动主减速器行星传动系统可靠性框图
2 失效单元可靠性模型
为计算各失效单元的可靠度,必须正确建立各失效单元的可靠性模型,包括齿轮失效单元的可靠性模型和轴承失效单元的可靠性模型。
2.1 齿轮失效单元的可靠性计算模型
按国标GB/T3480-1997,将除载荷F t及使用系数KA外的其他各尺寸参数和修正系数按常量处理,这时齿轮节点处的计算接触应力以及齿根弯曲应力可写为Ft和KA的函数。统一记为

上两式中各符号含义详见GB/T3480-1997。其中,vi、wi为常数。设此时对应的强度随机变量为ri,随机变量Ft、KA、ri均服从正态分布,则第i个失效单元的极限状态函数gi=ri-Si(F t,K A)。由JC法可以求出相应的可靠性系数βi,则第i个齿轮失效单元的可靠性计算模型为

2.2 轴承失效单元的可靠性计算模型
大量试验证明,滚动轴承的接触疲劳寿命服从三参数Weibu ll分布[22],则相应的可靠度函数为
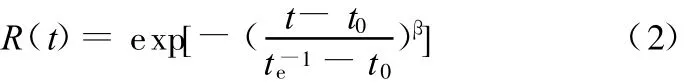
式中,t为不同可靠度时的轴承寿命;t0为最小寿命(位置参数);te-1为特征寿命(尺度参数);β为 Weibu ll斜率(形状参数),一般球轴承β=10/9,圆柱滚子轴承β=3/2,圆锥滚子轴承β=4/3。
式(2)即为轴承失效单元的可靠性计算模型。这样,在已知轴承的运转时间t后,便可求出相应的可靠度R(t)。
3 系统可靠性模型
3.1 机械传动系统可靠性一般计算模型
为准确求得机械传动系统的可靠度,必须考虑系统中多种失效模式间的相关性,而这种相关性往往是多方面的,如载荷上的相关、刚度上的相关、尺寸上的相关等。设各失效模式间关于m个因素相关,这些因素称为广义载荷,它们都是随机变量,分别记为 N1,N2,…,Nm,写成向量形式为N=(N1,N2,…,Nm),其概率密度函数分别为fN1(N 1),fN2(N2),…,fNm(Nm)。在第 i种失效模式下载荷所产生的应力为Si(N),对应于该模式下的强度随机变量为 r,其概率密度函数为fi(r)。当各个广义载荷为确定值时,即N=N0=(N10,N20,…,Nm0)时,第i种失效模式的可靠度为

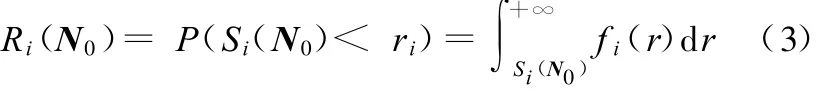
若各失效模式间关于强度是相互独立的,失效模式总数为n,则各失效单元均可靠的概率为

式(7)即为在多失效模式及多因素相关条件下系统可靠性的一般计算模型。一般地,各失效模式间的主要相关因素个数m不大于2或3,式(7)的多重积分不会超过三重,采用数值积分计算,可以求得系统的可靠度。
3.2 盾构机刀盘驱动多级行星传动系统可靠性计算模型
由于盾构机刀盘驱动多级行星传动系统中失效单元数较多,故为使计算简化,将其他修正系数(如动载系数、弹性系数等,不是影响模式间相关的主要因素)按常量处理。考虑主要因素,即载荷和使用系数的相关性,则由各齿轮失效单元组成的系统的可靠性计算模型为

为简化计算,假定载荷、使用系数和强度均服从正态分布。即KA~ N(uKA,σKA),Ft~ N(uFt,σFt),r~ N(ur,σr)。则式(8)经变换推导可表示为

其中,fFt(Ft)、fKA(KA)分别为Ft、KA的概率密度函数;uri、σri分别为第i种失效模式下强度的均值和标准差;Si(F t,K A)为第i种失效模式下的应力;Ft为端面内分度圆上的名义切向力,且有

式中,Ts为太阳轮轴上的输入转矩;Kp为行星轮间载荷分配不均匀系数;ds为太阳轮分度圆直径。
可见,式(9)中被积函数表达式较为复杂,含24个积分的乘积,但在计算机上求解仍然是很方便的。一方面,按式(1)分别计算系统中24个齿轮失效单元的可靠度,对可靠度较高的单元可以略去不计,减少被积函数表达式中积分的数目;另一方面,编程计算可在MATLAB中进行,直接调用其normcdf函数计算正态分布的累积概率值。对于积分限的选取,按Ft和KA的实际取值,下限分别取为0和1,上限分别取uFt+(5~10)σFt和uKA+(5 ~ 10)σKA为宜 。最后,采用Simpson数值积分算法,可以计算出可靠度R的准确值。
由式(2)可计算出三级行星轮轴承的可靠度,分别记为 Rg1、Rg2、Rg3。由于轴承单元的失效与齿轮单元的失效相关性较小,故计算时可认为两者是相互独立的。则整个盾构机刀盘驱动行星传动系统的可靠度为

4 计算实例
某盾构机刀盘驱动主减速器采用三级2KH行星传动串联形式,输入端太阳轮轴上的扭矩为Ts=1489±446.7N◦m,载荷分配不均匀系数K p=1.1,使用系数K A=1.35±0.133 65。1至3级行星轮的个数n p分别是3、4、4。已知载荷、使用系数、强度均服从正态分布,其他参数为常量。太阳轮和行星轮材料均为17Cr2Ni2M o,内齿轮材料为30Cr2Ni2M o。选用40℃时运动黏度为320mm2/s的润滑油。该主减速器的设计寿命按10 000h计算,其他设计参数如表2所示。计算该主减速器行星传动系统的可靠度。
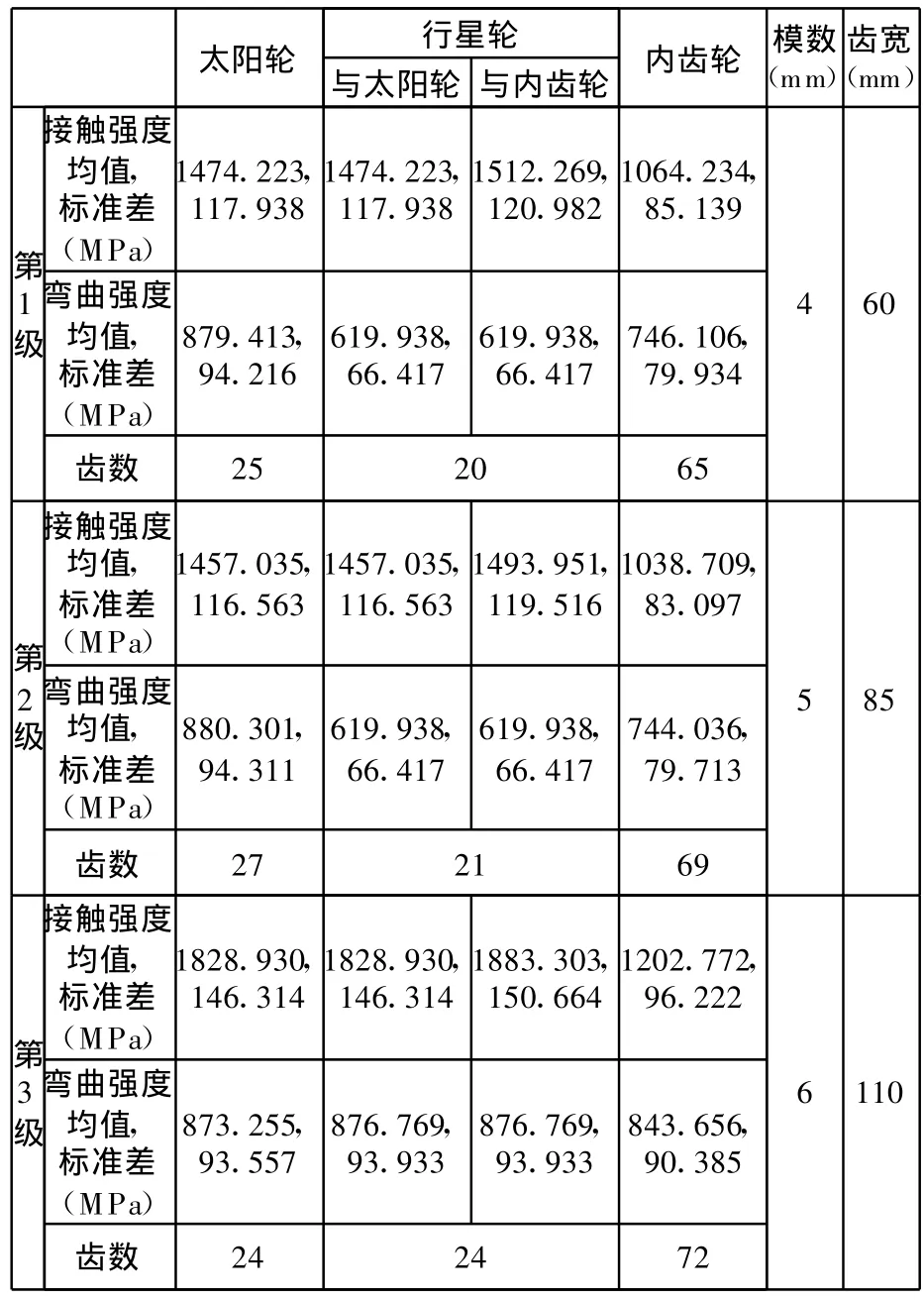
表2 盾构机刀盘驱动主减速器传动系统设计参数
(1)计算载荷及使用系数的均值和标准差。按式(10)分别计算载荷的均值和标准差,得F t~N(10 919,1091.9)N。按3σ法则可求出使用系数的均值和标准差,得KA~N(1.35,0.044 55)。
(2)计算各齿轮失效单元的可靠度。按式(1)计算各齿轮失效单元的可靠度,结果如表3所示。
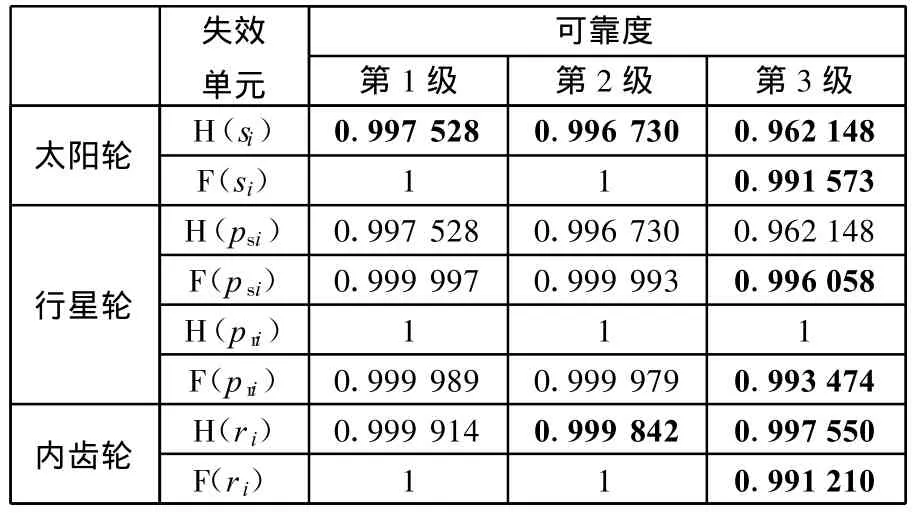
表3 传动系统中各齿轮失效单元的可靠度
可见,在24种失效单元中太阳轮弯曲疲劳单元、行星轮(与内齿轮啮合)接触疲劳单元以及内齿轮的弯曲疲劳单元的可靠度均为1,即不会发生这些模式的失效,计算时不予考虑。同时,对于可靠度大于99.99%的失效单元可认为比较可靠,计算时也不予考虑。另外,由于太阳轮接触疲劳失效和行星轮(与太阳轮啮合)接触疲劳失效是两个完全相同的事件,因此可以作为一种失效模式来处理。这样24种失效模式经化简变为9种失效模式。如表3中黑体数字所示。
(3)计算轴承失效单元可靠度。按式(2),在已知设计寿命t=10 000h的情况下,可以分别求出各级行星轮轴承对应的可靠度,如表4所示。

表4 各级行星轮轴承失效单元的可靠度
(4)系统可靠度计算。首先由式(9)计算传动系统中齿轮失效单元总的可靠度R≈0.934 392。为验证计算结果的准确性,采用M onte-Carlo法对其进行仿真模拟。结果如表5所示。

表5 按M onte-Carlo方法模拟的可靠度结果
可见,随着模拟次数的增加,可靠度在数值上趋于稳定,当模拟次数达到200万次时,可靠度值与式(9)的计算结果相接近,由此验证了上述计算模型的正确性。
由式(11),整个盾构机刀盘驱动三级行星传动系统的可靠度为

5 结论
(1)应用应力-强度干涉理论推导出了在多失效模式及多因素相关条件下机械传动系统可靠性的一般计算模型。并运用该模型建立了盾构机刀盘驱动多级行星传动系统的可靠性计算模型,求取了该系统可靠度的准确值。由于系统中失效单元数较多,故计算时主要考虑了可能发生失效的单元;同时,由于各失效模式间的相关性是多方面的,故计算时主要考虑了关于载荷和使用系数的相关性。
(3)由表3可知,单元可靠度在各级传动系统中分布不均匀,第1级、2级的单元可靠度较高,而第3级的单元可靠度偏低,且可能失效的单元数较多,从而导致整个盾构机刀盘驱动多级行星传动系统的可靠度偏低。因此,需要对系统中各单元的可靠度进行重新分配,对系统进行可靠性优化设计,提高整个传动系统的可靠性。
[1] 邹积波.从盾构施工谈“可靠性工程”的重要性[J].都市快轨交通,2003(3):19-22.
[2] 杜小平.零件失效相关时机械传动系统的可靠性计算[J].机械传动,1994,18(3):1-4.
[3] Xie Liyang.Pipe Segment Failure Dependence Analysis and System Failure Probability Estimation[J].Pressure Vesseland Piping,1998,76:483-488.
[4] Jussi K V.An Implicit Method for Incorporating Common-cause Failures in System Analysis[J].IEEE Transactions on Reliability,1998,47(2):173-180.
[5] Place C S,Strutt JE,Allsopp K,et al.Re liability Prediction o f Helicop ter Transmission Systems Using Stress-strength Interference with Underlying Damage A ccumulation[J].Quality and Reliability Engineering International,1999,15:69-78.
[6] Levitin G.Incorporating Common-cause Failures into No Repairable Multi-state Series-parallel System Ana lysis[J].IEEE Transactions on Reliability,2001,50(4):380-388.
[7] Ditlevsen O.Narrow Reliability Bounds for Structural System[J].Journal o f Structural Mechanics,1979,7(4):453-472.
[8] Ang H S,Tang W H.Probability Concep ts in Engineering Planning and Design[M].New York:John Wiley&Sons,1984.
[9] Rackwitz R,Flessler B.Structural Reliability under Combined Random Load Sequence[J].Computers and Structures,1979,9(5):489-494.
[10] 李云贵,赵国藩.结构体系可靠度的近似计算方法[J].土木工程学报,1993,26(5):72-78.
[11] 成刚虎,喻天翔,张祖明.多模相关的两种 RD理论特点和应用分析[J].西安理工大学学报,2003,19(2):162-165.
[12] 康海贵,张晶,张小庆.体系可靠度计算中改进的等价平面法[J].计算力学学报,2010,27(1):141-146.
[13] 王正,谢里阳,李兵.考虑共因失效的机械零部件可靠性模型[J].机械设计,2007,24(1):4-5,69.
[14] Lewis E E.A Load-capability InterferenceM odel for Common-mode Failures in 1-out-of-2:G Systems[J].IEEE Transactions on Reliability,2001,50(1):47-51.
[15] Xie Liyang,Zhou Jinyu,Hao Changzhong.Systemlevel Load-strength Interference Based Reliability Modeling ofk-out-of-n System[J].Reliability Engineering and System Safety,2004,84:311-317.
[16] 吴立言,王步瀛.机械传动系统可靠性分析[J].机械传动,1993,17(2):18-20.
[17] 孙志礼,陈良玉,张钰,等.机械传动系统可靠性设计模型[J].东北大学学报(自然科学版),2003,24(6):548-551.
[18] 王正,康锐,谢里阳.以载荷作用次数为寿命指标的失效相关系统可靠性建模[J].机械工程学报,2010,46(6):192-198.
[19] 孙志礼,陈良玉.实用机械可靠性设计理论与方法[M].北京:科学出版社,2003.
[20] 陈历祥.行星齿轮轮系的可靠性[J].机械传动,1983(2):10-15.
[21] 陈琳,杨绍奎.机械传动系统可靠性分析的权函数法[J].石油机械,1997,25(10):19-21.
[22] 朱文予.机械可靠性设计[M].上海:上海交通大学出版社,1992.
Reliability Model of Shield M achine Cutter Drive Mu lti-stage Planetary Transm ission System Considering Failure Relevance
Zhao Yong1Qin Datong1Wu Wenhui2
1.The State Key Laboratory of M echanical T ransmission,Chongqing,400044
2.CITIC Heavy M achinery Co.,Ltd.,Luoyang,Henan,471039
Multi-failurem odes of each gear and multifactor relevance were existed in a p lanetary gear transmission.Based on the stress-strength interference theory,general reliability com putation model for mechanical transmission system was presented under conditions ofmulti-failuremodesand multifactor relevance,and applied to the reliability analysis for them ulti-stage p lanetary transmission system used in shield machine cutter drive.Reliability models for each failure units like gearsand bearings were established first.The reliability model of transmission system was obtained considering main failuremodesand failure relevance of load and app lication factor,and Monte-Carlom ethod was used to simulate the result.The results demonstrate that the model can evaluate the reliability of shield machine cutter drivemulti-stage planetary transmission system accurately.
planetary gear transmission;stress-strength interference theory;reliability of system;multi-failuremodes relevance
TB114.3;TH122
1004—132X(2011)05—0522—06
2010—05—10
国家高技术研究发展计划(863计划)资助项目(2007AA041802)
(编辑 袁兴玲)
赵 勇,男,1978年生。重庆大学机械传动国家重点实验室博士研究生。研究方向为机械传动系统可靠性、随机有限元。秦大同,男,1956年生。重庆大学机械传动国家重点实验室教授、博士研究生导师。武文辉,男,1960年生。中信重型机械公司齿轮研究所所长、高级工程师。

