块图中的无权1-中心问题

张晓芹， 康丽英

(上海大学理学院，上海200444)

选址问题是运筹学中的一个基本研究课题，在物流设施规划、通讯系统设计等诸多领域具有十分广阔的应用背景.p-中心问题属于设施选址问题，指在网络图中放置p个设施，使得每个客户到达最近设施的最大权距离最小.对任意网络图，V和E分别表示网络图N的顶点集和边集，n=|V|和m=|E|分别表示N的顶点数和边数.为叙述方便，引入符号Γ/Δ/p，其中Γ表示设施集合，Δ表示客户集合，p表示需要放置的设施个数.一般地，Γ∈{V，E}，Δ∈{V，E}.这表明设施和客户的位置可能是图N的顶点，也可能是边上任意一点.若所有客户的权值均为1，则称该问题为无权中心问题.

1979年，Karive等［1］证明了一般图的p-中心问题是NP-难的.他们还进一步研究了一般图的加权E/V/1问题和V/V/1问题，并相应地给出了复杂性为O(mnlog n)和O(mn+n2log n)的算法.后来，Karive和Hakimi又为一般图的加权E/V/p问题设计了一个O(mpn2p-1log n/(p-1)!)算法.Tamir于1991年在文献［2］中将上述算法的复杂性改善为O(mpnplog nα(n))，其中α(n)表示Ackermann函数的逆.此外，还有许多学者致力于特殊图的研究.到目前为止，关于树中无权V/V/p，E/V/p和V/E/p问题的最有效算法的复杂性均为O(n)［3］.而对于树中加权的p-中心问题，Megiddo等［4］证明了V/V/ p问题可以在O(nlog2n)时间内解决.而Jeger［5］则为V/V/p和E/V/p问题设计了一个 O(pnlog n)算法.仙人掌图中p-中心问题的研究可参阅文献［6］.本工作主要研究块图中无权E/V/1中心问题，并给出一个线性时间算法.

1 基本定义与问题模型

本工作所研究的图均为有限无向简单图，文中凡未加定义的术语和符号可参阅文献［7］.对任意图N=(VN，EN)，VN和EN分别表示N的顶点集和边集.在N中，一个点x可能是N的顶点，也可能是N的边上的任意一点.对N中任意2个点x和 y，PN(x，y)表示连接x和y的最短路，dN(x，y)表示x和y 2点间的距离，即PN(x，y)的长度.若x和y之间没有路相连，则dN(x，y)=∞.对于子集U⊆VN，N［U］表示由U导出的子图.

若图N中任意2个顶点之间都存在路，则称N是连通的.顶点v称为N的割点，如果删除v以及与v相关联的边会增加连通分支的个数.图N的块是指不含割点的极大连通子图.文献［7］指出每个图都是它的所有块的并.若图N的每个块都是完全子图，则称N为块图［8-9］.图1(a)给出一个块图N，其包含的4个块分别为B1=N［{v1，v2，v3，v4}］，B2= N［{v4，v5，v6}］，B3=N［{v3，v7}］和 B4=N［{v3，v8}］.本工作总是研究连通块图N，且图N中每条边uv—的长度均为1(若无特别说明，以下讨论均含此假定).

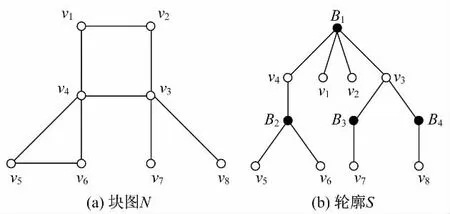
图1 块图N及其轮廓S的示意图Fig.1 Illustration of block graph N and its skeleton S

块图N中无权的E/V/1中心问题可描述如下：找到一个点x*∈EN，使得目标函数

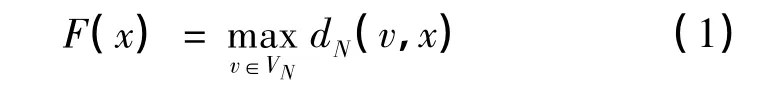
最小.

为了解决上述问题，本工作采用文献［10］中提出的块图N的轮廓S=(VS，ES).如图1(b)所示，S的每个顶点代表N的一个顶点或者一个块.对于N的每个顶点v和块B，如果v∈B，则S中有一条长度为1的边连接顶点v和B.由此可知，连通块图的轮廓是一棵树.若|VN|＞1，则S的所有叶子点都代表N的顶点.Aho等在文献［11］中证明了一个块图的轮廓可通过深度优先搜索方法在线性时间内构造出来.

由轮廓S的构造易得，其顶点集VS被分成2个互不相交的子集VN和β，其中β表示块图N中所有块的集合.本工—作定义S中的最长路为S的直径.当从S中删除边xy 时，用S(x，y)和S(y，x)分别表示包含顶点x和y的2棵子树.

2 块图中的无权1-中心问题

本节将通过研究块图的结构性质，证明块图中无权的E/V/1中心问题可以在线性时间内解决.基于轮廓S的特殊构造以及文献［12］中关于树的中心与直径的结论，现归纳S的一些基本性质.

性质1 设x和y为轮廓S的2个顶点，若x，y∈VN，则dS(x，y)=2dN(x，y).

性质2 若PS(x，y)为轮廓S的一条直径，则x，y∈VN，且dS(x，y)为偶数.

性质3 若PS(x，y)为轮廓S的一条直径，c为S的1-中心，则c为PS(x，y)的一个顶点，且满足dS(c，x)=dS(x，y)/2.

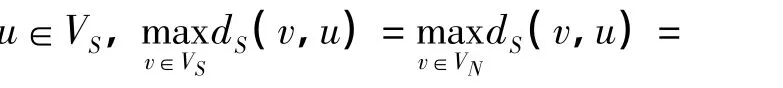
以下简称1-中心为图的中心.设c为轮廓S的中心，根据性质3可得，c是S直径上的一个顶点，因此，c∈VN，或者c∈β.

首先，考虑c∈VN的情况.

定理1 设c为轮廓S的中心，若c∈VN，则c为块图N的中心.

证明 因为c∈VN，根据性质1和4，可得

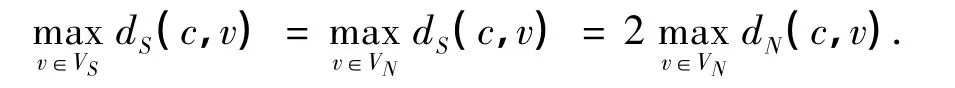
又由c为轮廓S的中心，可得

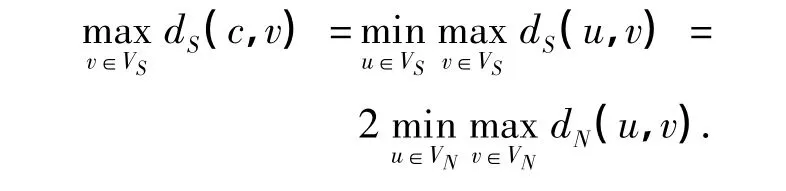
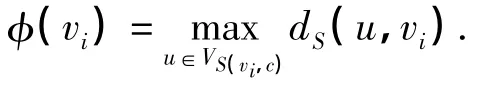
证明 在轮廓S中，令ui是子树S(vi，c)的一个顶点，且满足dS(vi，ui)=φ(vi)，i=1，…，dS(c)，如图2(a)所示.在块图N中，令Ni是N的一个子图，使得Ni的每个顶点和块都被S(vi，c)的一个顶点所表示，反之亦然，如图2(b)所示.由φ(vi)的定义可知，ui为Ni中距离vi最远的一个顶点.

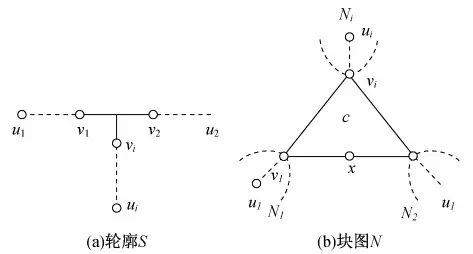
图2 定理2证明的示意图Fig.2 Illustration of proof of Theorem 2

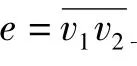
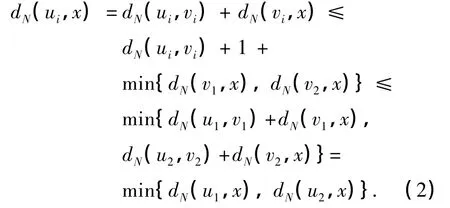
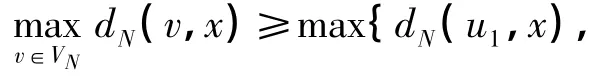
基于以上讨论，下面给出块图中无权E/V/1中心问题的求解算法UCBG.

输入：一个边长为1的连通块图N;

输出：块图N的中心c*.

(1)构造N的轮廓S;

(2)找出S的中心c;

(3)若c∈VN，则c*=c;

(4)若c∈B，则从S中删除顶点c以及与c相关联的边，得到子树S(v1，c)，…，S(vdS(c)，c);

(6)找出序列φ(vi)i中最大的3个数，从大到小排列，依次记为φ(vj)，φ(vk)和φ(vl);

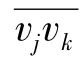
(8)若φ(vj)=φ(vk)=φ(vl)，则c*为N中块c的任意一个顶点;

(9)结束.

定理3 边长为1的块图中无权E/V/1中心问题可以在线性时间内解决.

证明 该定理的证明归结为算法UCBG的正确性与复杂性分析.定理1和2可直接说明算法UCBG的正确性.下面逐行分析算法的运行时间.

第1行可利用深度优先搜索方法进行构造，需要O(|VN|+|EN|)时间.第2行可利用Handler算法［13］求解，需要O(|VS|)时间.第4行，所有子树S(vi，c)可在O(|VS|)时间内得到.对任意整数1≤i≤dS(c)，φ(vi)可在O(|VS(vi，c)|)时间内计算出来.因此，第5行总共需要O(|VS|)时间，第6行只需经过3次求最大值运算，即可获得φ(vj)，φ(vk)和φ(vl)，所需时间为O(dS(v))，而第3，4，7和8行只需常数时间.又因O(|VS|)=O(|VN|+|B|)= O(|VN|)，所以，算法UCBG的复杂性为O(|VN+ EN|).

最后，通过求解图1(a)中块图N的1-中心对上述算法进行说明.块图N的轮廓S如图1(b)所示.根据Handler算法，最长路P(v5，v7)的中点B1是S的中心.因为B1∈B，依照算法的第4行，从S中删除顶点 B1以及与其相关联的边，得到子树S(v4，B1)，S(v1，B1)，S(v2，B1)和 S(v3，B1).由φ(vi)的定义得φ(v4)=2，φ(v1)=0，φ(v2)=0，φ(v3)=2，从而 φ(v4)=φ(v3)＞max{φ(v1)， φ(v2)}.根据算法的第7行，图1(a)中边的中点是块图的中心.

3 结束语

通过分析块图中心与轮廓中心的关系，本工作解决了块图中无权的E/V/1中心问题，并为其设计了线性时间算法.对任意p≥2，块图中无权的E/V/p问题能否类似地解决是一个比较有趣的问题，有待于进一步研究.此外，块图中加权的p-中心问题也是一个值得探讨的问题.

［1］ KARIVO，HAKIMIS L.An algorithmic approach to network location problems—(I) the p-centers［J］.SIAM J Appl Math，1979，37：539-560.

［2］ TAMIR A.Improved complexityboundsforcenter location problems on networks by using dynamic data structures［J］.SIAM J Discrete Math，1991(4)：34-38.

［3］ FREDERICKSONG N.Parametric search and locating supply centers in trees［C］∥ Proceedings of the 2nd Workshop on Algorithms and Data Structures.Berlin：Springer，1991：299-319.

［4］ MEGIDDON，TAMIRA，ZEMELE，etal.An O(nlog2n)algorithm for the kth longest path in a tree with applications to location problems［J］.SIAM J Comput，1981，10(2)：328-337.

［5］ JEGERM，KARIVO.Algorithms for finding p-centers on a weighted tree(for relatively small p)［J］.Networks，1985，15(3)：381-389.

［6］ BEN-MOSHEB，BHATTACHARYAB，SHIQ S，et al.Efficient algorithms for center problems in cactus graphs［J］.Theoretical Computer Science，2007，378(3)：237-252.

［7］ BONDYJ A，MURTYU S R.Graph theory with applications［M］.London：MacMillan，1976.

［8］ HUNGR W.Optimal vertex ranking of block graphs［J］.Information and Computation，2008，206：1288-1302.

［9］ WONGP K.Optimal path cover problem on block graphs［J］.Theoret Comput Sci，1999，225：163-169.

［10］ KANGL Y，CHENGY K.The p-maxian problem on block graphs［J］.J Comb Optim，20：131-141.

［11］ AHOA V，HOPCROPTJ E，ULLMANJ D.The design and analysis of computer algorithms［M］.Reading：Addison-Wesley Publishing Company，1976：84-86.

［12］ WUB Y，CHAOK M.Spanning trees and optimization problems［M］.Florida：CRC Press，2004：1-23.

［13］ HANDLERG Y.Minimax location of a facility in an undirected tree graph［J］.Trans Sci，1973，7(3)：287-293.