浅谈弹性地基梁的解析法

卢晓莉

(泰山职业技术学院建筑工程系，山东泰安 271000)

在求解软土地基上结构的静力问题时，常用方法有解析法、半解析法以及数值解法.解析法属于精确解法，它的基本思想是分别对结构的控制方程和地基模型的控制方程解析的求解，然后再满足结构和地基接触面的位移和应力的连续性条件和结构的边界条件，即可获得问题的全部解答.

1 反力直线法

反力直线法［1］是一种近似的方法，该法假定地基反力是按直线规律分布的，其地基反力图形在对称荷载作用下是矩形的，在偏心荷载作用下是梯形的，如图1所示.反力直线法中基础梁的计算问题是一个静定问题，根据静力平衡条件就很容易计算出反力的数值，具有计算简单方便的优点.由于该方法没有考虑基础梁和地基之间的变形协调，因而其计算结果是不准确的，在设计重要的建筑物时不宜采用，通常只在初步估算或设计不太重要的基础梁的时候使用.

图1 反力直线法的地基反力假设

2 基于文克尔地基上的初参数法

文克尔地基上的初参数法［2］是一种运用较为广泛的计算方法，它是通过考虑一受荷载的弹性地基梁的变形情况，取其中一个无穷小的单元，考虑单元的平衡条件，列出平衡方程.同时结合在材料力学中梁受弯的微分公式求出通解，然后根据具体的边界情况以及受力情况求出内力.例如文克尔地基上的无限长梁的通解为

而集中力作用下的无限长梁(如图2所示)，利用边界条件以及受力情况，最后可得

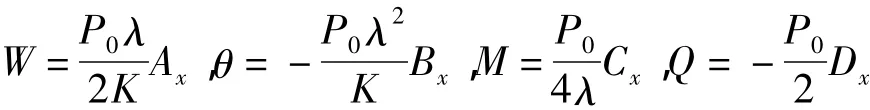
式中

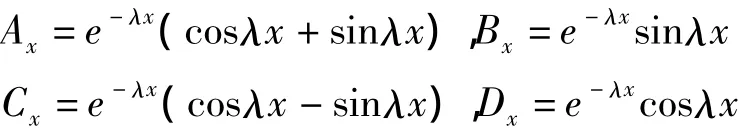
图2 受集中力作用下文克尔地基上的无限长梁

3 弹性半空间上梁的级数解法

如图3所示一基础梁，受到任意分布荷载q(x)，基础反力p(x)沿宽度方向为均布地基上梁的挠曲线微分方程为:

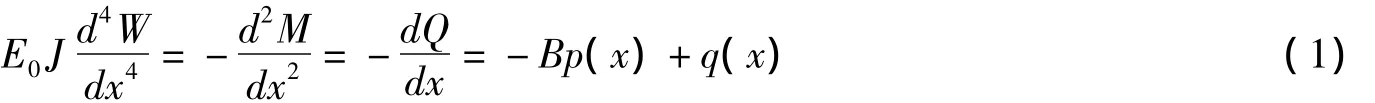
弹性理论平面应力问题的弗拉曼(Flamant)解［3］

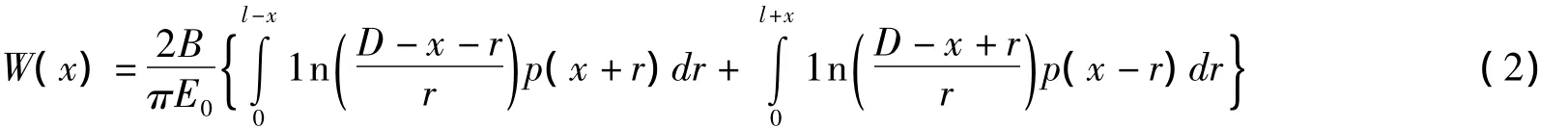
弹性半空间地基表面的竖向位移为:

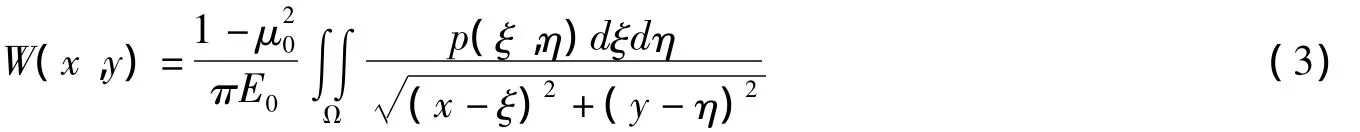
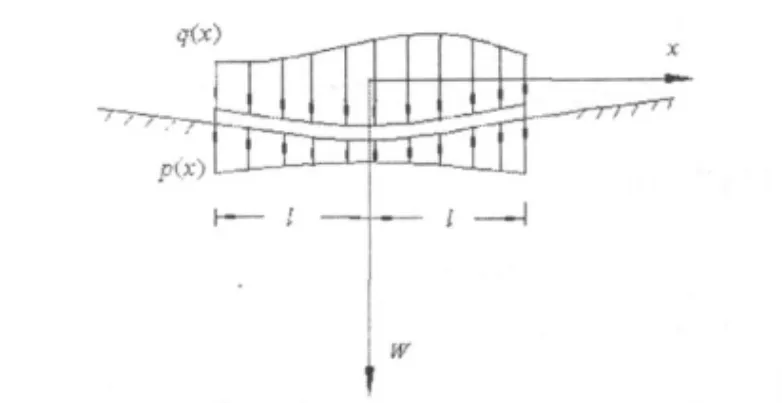
图3 弹性半平面上的梁

可作为弹性半空间模型在平面应力问题下的特征函数.将式(2)与式(3)代入式(1)则得到不同问题中地基上梁的基本方程.

(1)平面应力问题

(2)平面应变问题

以上两式中，D为任意选定的参照点的坐标.上述情况下的基本方程都是关于p(x)的微分积分方程，除应满足梁的边界条件外，还应满足静力平衡条件.

在平衡条件和梁的边界条件下求解微分积分方程是及其困难的.哥尔布诺夫－彼沙道夫等提出的级数解法有效地解决了这一问题［4］，并就若干典型情况给出了大量的内力无量纲计算表格工程设计中不必做复杂的运算，查表后做简单的量纲换算即可.

级数法的基本思路是先把地基反力p(x)近似地表示为有限项的幂级数:

式中ai为n+1个未知的待定系数.由平衡方程可使未知数减少两个，余下n－1个则通过n－1个点处梁的挠度与地基沉降相等的条件列出n－1个，变形连续方程，因此问题归结为求解n+1个代数方程.

显然，当n→∞时，解答是精确的.但实际上这是不可能的，也没有必要这样做.当n为有限项时，解答是近似的，如果表格按n=11给出，精度已经相当高，足可以满足工程需要.

4 小结

本文重点介绍了反力直线法、初参数法、级数解法等具体的解析方法.在前人理论研究的基础上通过比较，总结出了各种方法适用的地基模型及其各自的优缺点，反力直线具有计算简单方便的优点.但是另一方面由于该方法没有考虑基础梁和地基之间的变形协调，因而其计算结果是不准确的，在设计重要的建筑物时不宜采用.初参数法和级数解法由于要积分，对于简单结构尚可，但是对于复杂一点的结构计算会相当麻烦，而且不一定能解决.因此，弹性地基上基础梁的发展方向应该是在解析方法的基础上加入计算机仿真，这样既可以节省时间，又可以保证计算精度.

［1］龙驭球.弹性地基梁的计算［M］.北京:人民教育出版社，1981.

［2］张子明.用初始函数法计算多层地基的位移和应力［J］.岩土工程学报，1986，8(4).

［3］徐芝纶.弹性理论［M］.北京:人民教育出版社，1960.

［4］田千里.平面问题弹性地基梁之简捷解法［J］.科学通报，1974，(5).