基于最小二乘映射的多参数结构问题快速计算方法
陈 沛 韩 旭 姜 潮 张 正
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
基于最小二乘映射的多参数结构问题快速计算方法
陈 沛 韩 旭 姜 潮 张 正
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
针对机械工程中复杂结构多参数问题,提出一种新的基于最小二乘映射的减基法。该方法通过在参数域采集样本点,计算系统在有限个样本点下的响应以构造减基空间,利用最小二乘映射把原方程向减基空间进行投影得到减缩方程,在减基空间快速求解该减缩系统,获得原问题的减缩解,并把减缩解还原到原空间,得到问题的近似解。当系统参数发生变化时,能通过减缩系统快速得到新参数下的响应,极大地提高了计算效率。最后将该方法用于赛车车架刚度计算,结果表明方法是有效且可靠的。
减基法;最小二乘映射;多参数问题;拉丁超立方采样
0 引言
工程设计和产品开发越来越注重优化设计,如何为众多的参数选择最合适的数值,这将在很大程度上影响产品的质量、性能及成本。优化设计的主要工作是性能的重复分析,每次系统几何参数或物理参数的改变,都需要对结构重新进行计算。对于复杂结构多参数系统而言,用传统的计算方法循环求解不同输入下的输出,计算费用非常高,因此,受制于计算成本,很难对结构系统进行自适应设计和优化,或对参数进行稳健的估计。目前解决这类问题的一条途径是对结构进行降阶建模和分析,如Guyan降阶法[1]、Ritz向量降阶法[2]、正常正交分解法[3]等,但这些方法在保持原模型的物理特性和提高效率上仍存在一定的局限性,即使是降阶后,求解仍比较耗时。
减基法作为一种新的快速计算方法,在20世纪70年代被提出,其基本思想是,当系统由多个参数来描述时,这些参数的不同组合会使系统方程有不同的解,而系统在新参数下的解可以用事先设计的样本参数组所对应解的线性组合来得到。近年来,不少学者对该方法进行了研究,Maday等[4-5]提出了减基法计算的预收敛理论;Rovas[6]把减基法应用于不同种类偏微分方程的求解中;Liu等[7]将减基法扩展到反问题中,并进行了相关研究。国内对该方法的研究很少,刘玉秋等[8]将修正减基法用于船舶设计,雷飞等[9]将减基法用于车身复杂结构大规模问题的快速分析。
上述文献中采用的减基法都是先构造减基空间,再通过Galerkin映射把原方程投影到低阶方程进行求解。本文在此基础上提出一种新的减基法:在获取减基空间后,利用最小二乘映射把系统特征矩阵及载荷向量向减基空间投影得到减缩系统,求解减缩系统并将解映射到原空间得到问题的近似解。本文以某赛车车架为例,分别通过计算耗时和误差对比,验证了该减基方法的可靠性和有效性。
1 基于最小二乘映射的减基法理论及算法
1.1 基于最小二乘映射减基法理论
对于大型结构静力学问题,有限元方法通常用偏微分方程弱形式的矩阵表示:

式中,Κ(μ)为刚度矩阵;U(μ)为场变量;F为载荷向量;μ为输入参数,对于多参数问题,μ为参数向量。
通过拉丁超立方采样,在参数域 Ω中采样N个参数点,得到集合

当采样方法科学,样本点数目选取合理时,所构造的减基空间具有良好的完备性,从而保障了降阶投影后原模型的物理特性不发生改变或缺失。因此,当参数域发生变化时,新参数下的解能用减基空间中基向量的线性组合表示,即

对于静力学问题,当参数发生变化时,结构对应的数学模型会发生相应的变化,即刚度矩阵改变。为了避免参数变化后重新进行前处理以及保证计算的高效性,将系统刚度矩阵显式分解成与参数相关的系数部分和与参数无关的矩阵部分,将刚度矩阵表示为
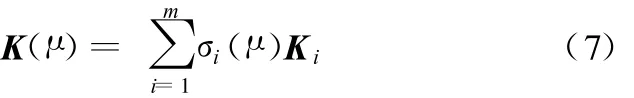
式中,σi(μ)为与参数相关的函数项;Ki(i=1,2,…,m)为刚度矩阵中的不变项;m为刚度矩阵分离项数。
当参数发生变化时,无需对结构重新进行前处理,只需要对与参数相关的系数部分进行修正即可快速得到新的系统矩阵。


式(13)和式(14)中,K i为刚度矩阵中不变项,F为载荷常向量,故A i j、B i的值恒定而不受参数变化的影响,只需在离线阶段计算一次,其结果可以在在线阶段反复调用。KN(μ)为减缩系统方程的刚度矩阵,FN为缩减系统方程的力向量。在经过上述最小二乘变换后,原线性系统由n×n阶降为了N×N阶,从而使问题求解计算量大大缩减。求解式(17)得到减缩系统的响应α(μ),将α(μ)回代式(4)即可得到原系统的近似响应。
1.2 基于最小二乘映射减基法计算流程
根据减基法计算特点,将计算分为离线计算与在线计算两部分。
(1)离线阶段。①对参数域进行采样并求解系统在样本点的解;②构造减基空间;③分离刚度矩阵,投影与参数无关的矩阵。
(2)在线阶段。①将参数无关矩阵与设计变量集成,构造新参数下的减缩系统;②求解减缩系统;③以减缩解为系数对解空间基向量进行线性组合,得到新参数下的近似解。
2 基于最小二乘映射减基法误差定义
由于减基法是通过求解高维问题降阶后的低维系统而快速得到原系统的近似解,所以在进行降阶的过程中必然存在数值误差。为了验证减基法的计算精度,在相同参数下比较有限元法计算结果和减缩计算结果,利用欧几里德范数定义相对误差:

3 赛车车架刚度计算算例
以某大学生方程式赛车的车架刚度计算为例,车架刚度是评价赛车可靠性及安全性的一个重要指标,它直接影响赛车能承受的最大载荷以及冲击韧性等,而车架材料及几何尺寸都是影响刚度的重要因素。当进行车架设计时,需要在各参数范围内选取多组参数组合,分别进行计算分析以找出最优设计方案。基于传统有限元的计算方法在参数改变时需要重新进行前处理并集成新的特征矩阵,不仅繁琐而且耗时,以减基法为基础的快速算法对处理此类多参数变化问题非常有优势。
根据车架各部位承受载荷状况的不同,该赛车车架的主要受力构件采用直径为25mm的空心圆钢管焊接而成,次要受力构件及支撑件采用直径为20mm的空心圆钢管焊接而成。取其壁厚作为设计参数,直径20mm的钢管壁厚t1变化范围为1.2~2.8mm,直径25mm的钢管壁厚t2变化范围为1.0~2.5mm。根据钢管加工过程包含的杂质元素及热处理工艺的不同[10],取其弹性模量E变化范围为192~320GPa,泊松比υ=0.33。计算边界条件如图1所示,约束 A点六个由度,B、C、D三点约束三个平动自由度,保留三个转动自由度,在车架顶部四个对称位置分别施加垂直向下的集中载荷,通过测量车架变形大小来计算车架刚度。用梁单元将车架离散成409个单元,371个节点,共2226个自由度。

图1 赛车车架及刚度计算边界条件
用拉丁超立方采样法在参数域采取10个样本点,用减基法把原来2226×2226的系数矩阵缩减为10×10的矩阵,大幅度提高了求解效率。计算过程用Fortran程序实现,采用减基法计算,离线计算时间为27.217s,在线计算时间为0.00016s,而用有限元法计算一次的时间为2.018s。当问题规模不大或计算次数不多时,减基法并不能充分体现出其优势。随着计算次数的增加,减缩系统的计算时间与有限元计算时间的比较见图2。由图2知,当计算次数大于某一临界值时,减缩计算的时间总是小于有限元计算时间,且随着计算次数的增加,减缩计算的优势越明显。在需要修改参数进行反复迭代的大规模计算过程中,采用减缩法能有效提高求解效率。

图2 减缩计算时间与有限元计算时间对比
为验证该减缩算法的稳定性,在参数域中随机选取50组参数组合:
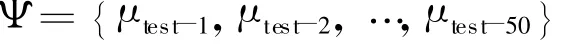
在10个基下分别计算其响应。选取图1中E点作为响应观测点,考虑位移变化较大的y方向和z方向,减缩计算与有限元计算结果相对误差分别如图3和图4所示。由图3和图4可知,所有参数点两个方向的误差均小于3.5×10-4,说明该方法对参数空间具有良好的适应性,同时表明通过拉丁超立方采样构造的减缩空间能较好地保持原系统的物理特性。
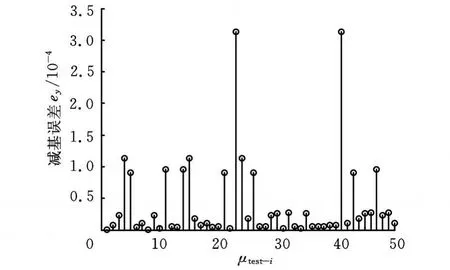
图3 不同参数组合下E点y方向误差

图4 不同参数组合下E点z方向误差
减缩计算误差与基空间维数之间的关系如图5和图6所示。同样选取y方向和z方向进行观测,图5和图6表明,最小二乘映射减基法与基于Galerkin映射的传统减基法相比,两者的最大减缩误差具有一致收敛特性,当基空间维数较低时,最小二乘映射减基法的精度略优于基于Galerkin映射的减基法,随着基空间维数的增加,两者的减缩误差都迅速减小并趋于一个稳定值,且之后再增加基向量的个数不会提高减缩精度。
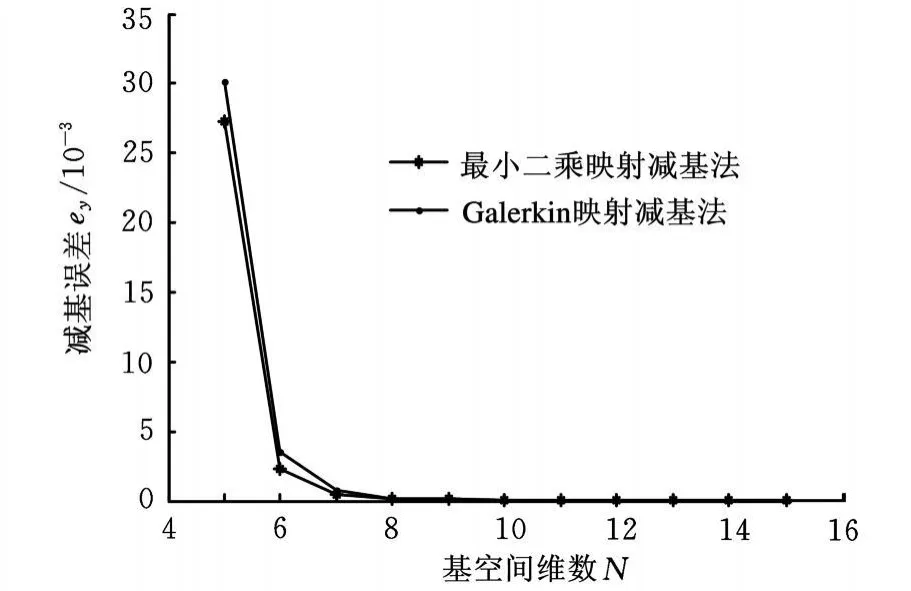
图5 y方向最大减基误差与基空间维数变化情况
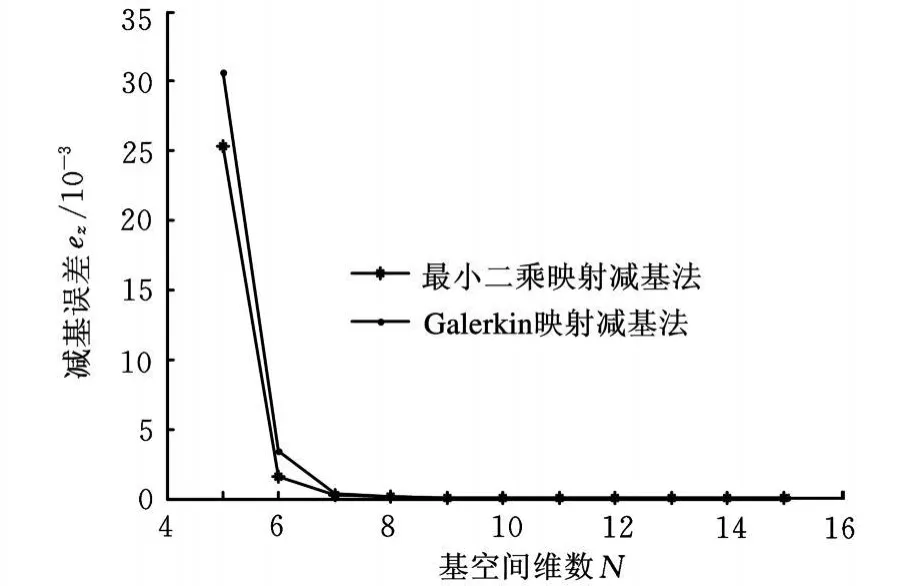
图6 z方向最大减基误差与基空间维数变化情况
4 结论
本文提出了一种基于最小二乘映射的减基法。该方法通过样本点求解构造减基空间,并将系统特征矩阵及载荷向量向减基空间进行最小二乘映射,从而将求解大规模线性方程组变为解小型线性方程组,与常规计算方法相比,节省了求解资源,有效地提高了计算效率,同时具有良好的计算精度。赛车车架的算例表明该方法是有效且可靠的。此外,该方法对大型复杂结构的反复迭代计算优势明显,故可应用到工程优化设计和反问题求解领域。
[1] Guyan R J.Reduction o f Stiffness and Mass Matrices[J].A IAA Journal,1965,3(2):380-381.
[2] Wilson E L,Bayo E P.Use of Special Ritz Vectors in Dynamic Substructure Analysis[J].AIAA Journal,1967,5(7):1944-1954.
[3] Machiels L,Maday Y,O liveiraI B,et al.Output Bounds for Reduced-basis Approximations of Symmetric Positive Definite Eigenvalue Prob lems[J].Comp tes Rendus de l'A cadém ie des Sciences-series I-Mathematics,2000,331(2):153-158.
[4] Maday Y,Patera A T,Turinici G.Global a Priori Convergence Theory for Reduced-basis Approximation of Single-parameter Symmetric Coercive Ellip tic Partial Differential Equations[J].C RA cad.Sci.Paris,S′erie I,2002,335(3):289-294.
[5] Maday Y,Patera A T,Turinici G.A Priori Convergence Theory for Reduced-basis App roximations o f Single-parameter Elliptic Partial Differential Equations[J].Journa l of Scientific Computing,2002,17(1/4):437-446.
[6] Rovas D V.Reduced-basis Output Bound Methods for Parametrized Partial Differential Equations[D].Cambridge,MA:Massachusetts Institute of Techno logy,2002.
[7] Liu G R,Zaw Khin,W ang Y Y.Rapid Inverse Parameter Estimation Using Reduced-basis Approximation with Asymp totic Error Estimation[J].Comput.Methods Appl.Mech.Engrg.,2008,197:3898-3910.
[8] 刘玉秋,聂武.修正缩减基法在船舶直接设计法中的应用[J].哈尔滨工程大学学报,1997,18(4):13-18.
[9] 雷飞,韩旭.车身复杂结构大规模问题的缩减计算[J].中国机械工程,2009,20(17):2127-2131,2141.
[10] 朱学仪,李卫.汽车用钢标准手册[M].北京,中国标准出版社,2008.
Efficient Method for Computation of Multi-parameterized Problem Based on Least Square Mapping
Chen Pei Han Xu Jiang Chao Zhang Zheng
State Key Laboratory of A dvanced Design and Manufacturing for Vehicle Body,H unan University,Changsha,410082
A new reduced-basis method based on the least square m apping was suggested to improve the efficiency of solving comp lex and multi-parameterized problems in mechanical engineering.In thismethod,sam pling pointsw ere obtained from the parameter domain,and a reduced-basis space w as constructed by com puting responses of the problem at these points.Then the least square mapping was emp loyed to conduct projection from original space onto the reduced-basis space.A reduced system was obtained and can be solved efficiently.By p ro jecting the reduced so lution back into the original space,an app roximate solution of the original system was obtained efficiently and accurately.Even w ith new variables,the solution can be obtained fastly by solving the reduced system.The numericalexamp le demonstrates that thism ethod is of validity and reliability.
reduced-basis method;least square mapping;m ulti-parameterized problem;Latin hypercube sam pling
TB121
1004—132X(2011)06—0706—04
2010—05—27
国家自然科学基金资助项目(10802028)
(编辑 苏卫国)
陈 沛,男,1985年生。湖南大学机械与运载工程学院硕士研究生。研究方向为结构分析的快速算法。韩 旭,男,1968年生。湖南大学机械与运载工程学院教授、博士研究生导师。姜 潮,男,1978年生。湖南大学机械与运载工程学院副教授。张 正,男,1981年生。湖南大学机械与运载工程学院博士研究生。

