对带有非局部边界条件的Dirac方程的迹的研究

梁银双，夏云青

(中州大学信息工程学院，郑州450044)

右边第二项的积分因单值性消失，则

3．csc(λ+m0)π的最简分式展开式如下:

所以问题(I)的迹公式为

1引言

关于Sturm－Liouvile算子的迹的研究，已积累了大量文献，不过大多数结果都是对局部方程局部边界条件得到的。1981年李梦如教授在文献［1］中得到下述带有非局部边界条件的S－L算子的迹公式:

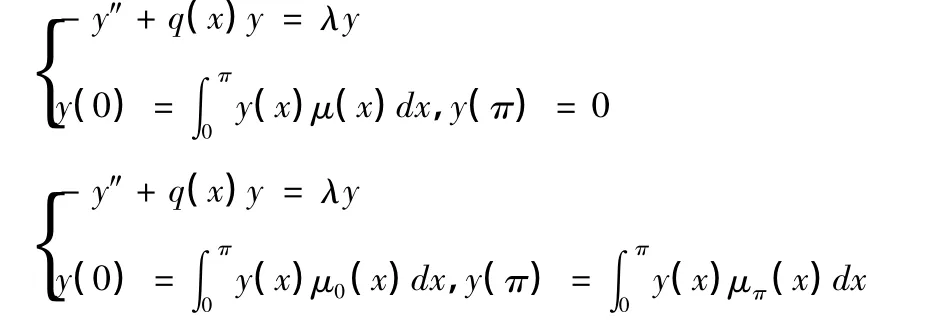
本篇论文主要研究下述问题渐近迹的公式:

p(x)，r(x)，μ(x) 均为［0，π］上的实值连续函数。

2问题(I)的整函数

我们先来考虑(I)的Cauchy问题(II):

引理1:由文献［2］知:问题(II)的解φ(x，λ)对λ的渐近式为:

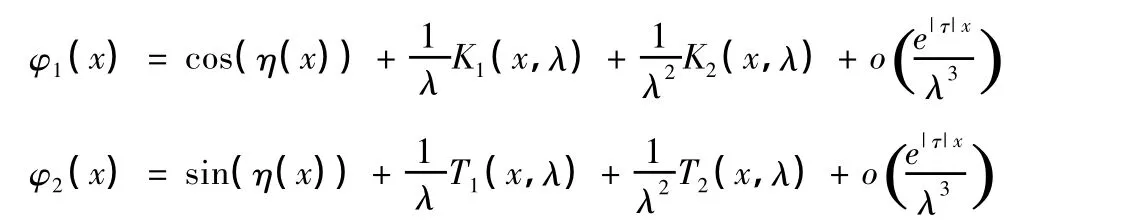
其中:

由此可知ω(λ)零点集合与(I)的特征值集合重合。下面计算整函数ω(λ)的渐近式。

由引理1知:

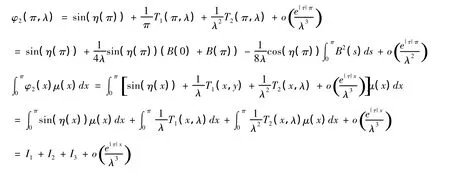
用分部积分可得:

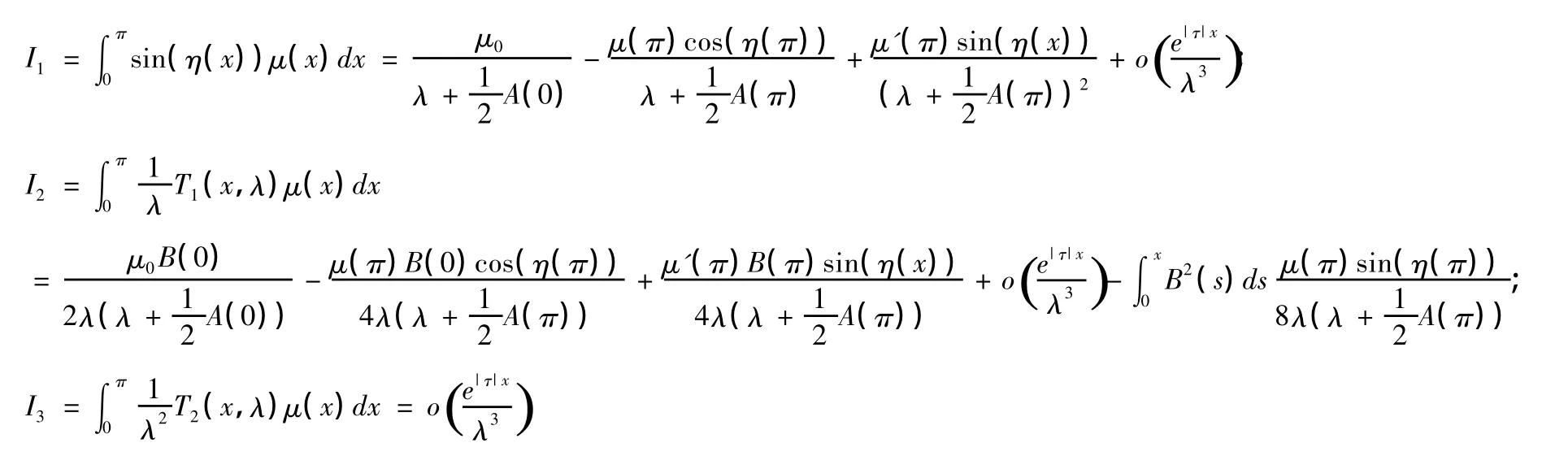
所以

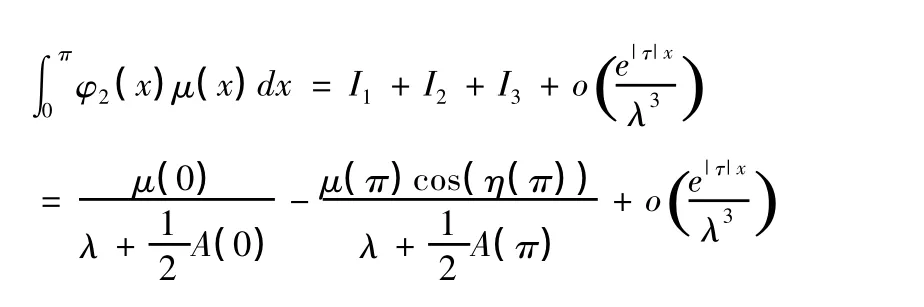
因而

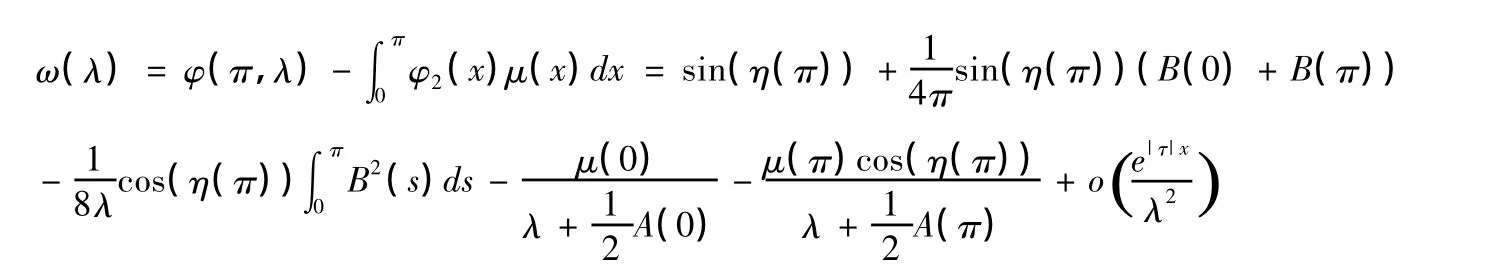
3问题(I)的迹

以下根据m0的不同取值来讨论问题(I)的迹公式:

(1)若m0≠0，且m0不是整数

ω0(λ) 的零点为:λn=n － m0，n=0，± 1，±2，…

因此

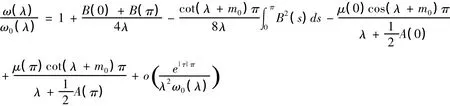
σ2= τ2=，在 CN上，以下三式均有界:

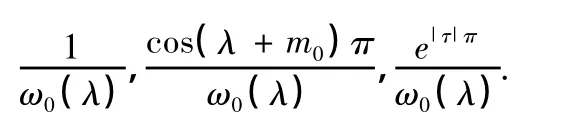
命题2:当N充分大时，ω(λ)与ω0(λ)在CN内有相同个数的零点。

证明:由引理2知:

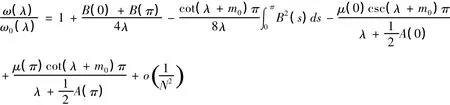
当 N充分大时，在Cn上有，因为ω(λ)，ω0(λ)是λ的整函数，ω0(λ)在CN上无零点，由Rouche定理知，ω(λ)和ω0(λ)在CN内有相同个数的零点。

定理1:对于问题(I)，设 p(x)，r(x) ∈ C(2)［0，π］，μ(x) ∈ C(3)［0，π］，则有如下迹公式:

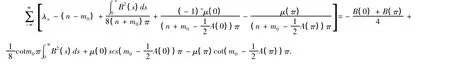
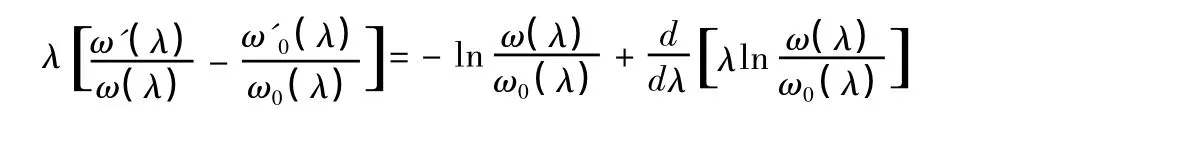
右边第二项的积分因单值性消失，则

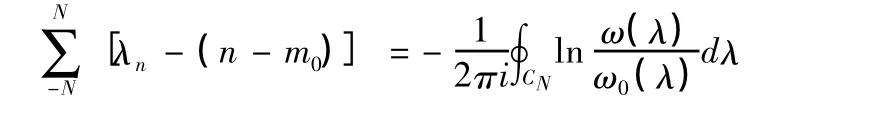
又

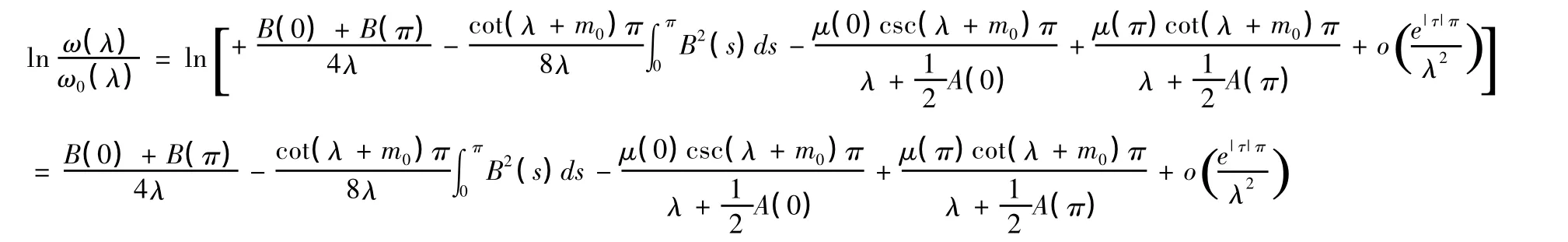
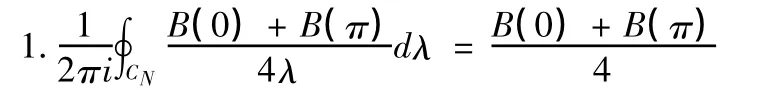
2．cot(λ+m0)π的最简分式展开式如下:

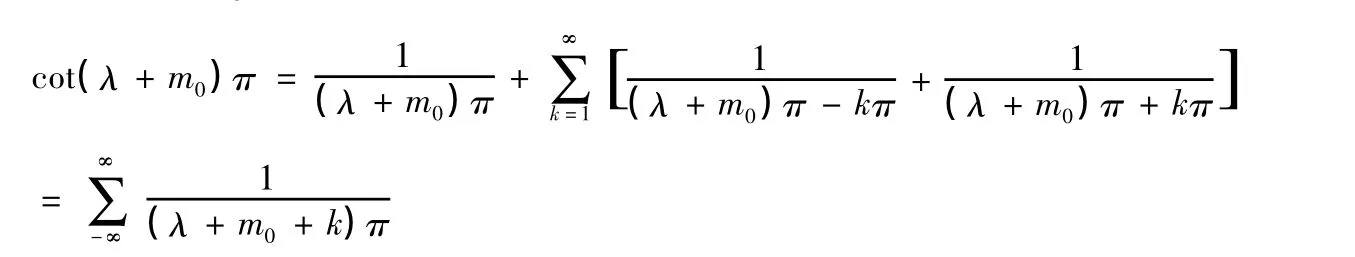
所以

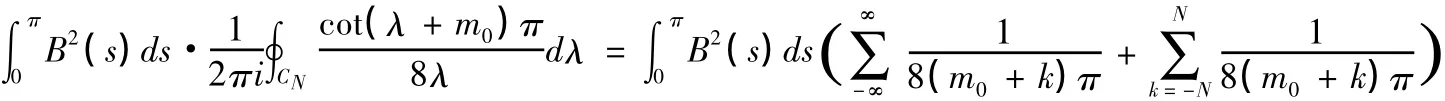
3．csc(λ+m0)π的最简分式展开式如下:

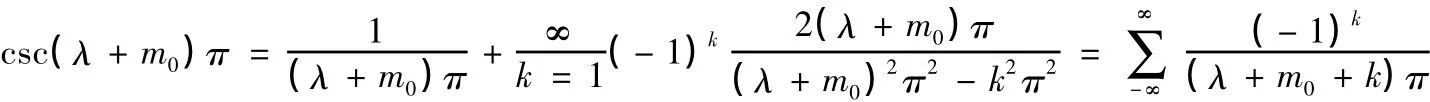
所以

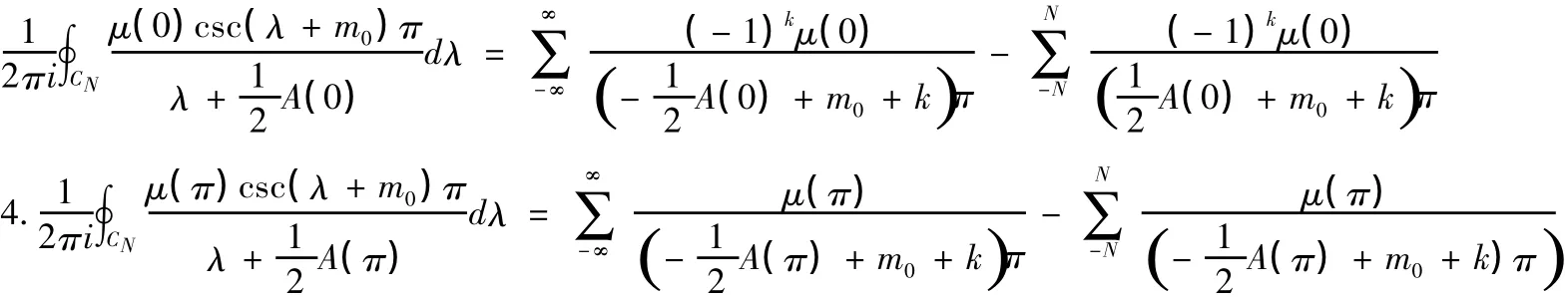
所以问题(I)的迹公式为

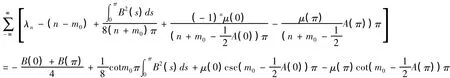
同理可得以下几种情况的迹公式:(2)若m0=0，问题(I)的迹公式为

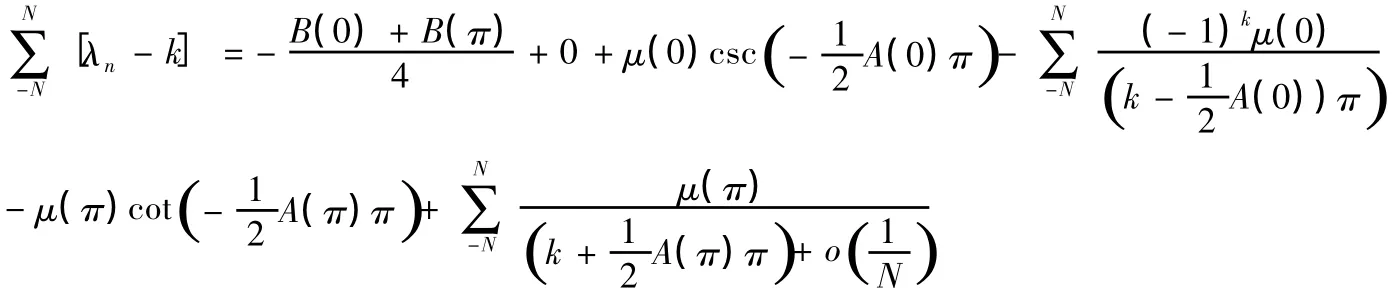
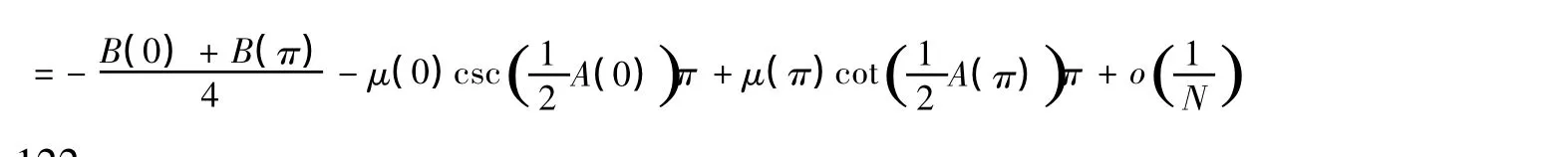
(3)m0≤Z且m0为偶数时，问题(1)的迹公式同m0=0的结果。

(4)m0∈Z且m0为奇数时，问题(1)的迹公式为:

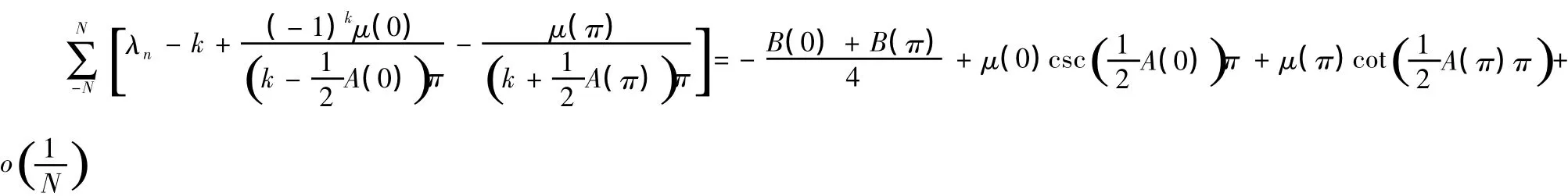
［1］李梦如．带有非定局边界条件的Sturm－Liouville算子的迹［J］．郑州大学学报:自然科学版，1981(1)．

［2］Abdukadyrov E．Calculation of the regularized spur for the Dirac system［J］．Journal of Moscow University，1967(4)．

［3］曹策问．微分算子的迹［J］．数学进展，1989，18(2):170 －178．

［4］曹策问．非自伴 Sturm －Liouville算子的渐近迹［J］．数学学报，1981，24(1):84 －94．

［5］曹之江．常微分算子［M］．上海:上海科技出版社，1985．

［6］Gelfand E M，Levitan B M．On trace identity for eigenvalue of differtial operator with sencod order［J］．DAN，1953，88:593 －596．［7］Levitan B M，Sargsjan I S．Sturm － Liouville and Dirac operators［J］．Kluwer Academic Publishers，1991(4)．

［8］纳依玛克．线性微分算子［M］．北京:科学出版社，1964．