突变分支过程常返性的一个证明
邹杨,许安见
(1重庆教育学院经济贸易系,重庆400067;2重庆邮电大学数理学院,重庆400065)
20世纪80’,Brockwell等人研究了一类具有突变率的生灭分支过程,其保守q-矩阵
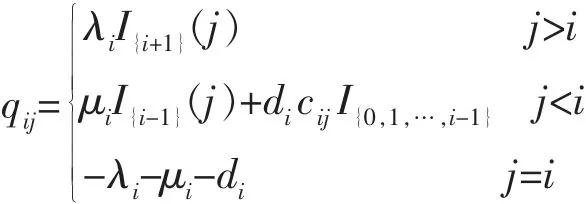
其中IA指集合A的特征函数,λi指生长系数,μi指灭亡系数,di为非负数表示突变率。假设μ0=d0=0,数cij(j=0,1,…,i-1,i≥1)是非负的且满足cij表示从状态i转移到状态j的突变概率。我们假设λi=a+ai,μi=0,di=d,i≥0,cij=1/i,j=0,1,…,i-1,得到一种具有固定突变率的线性生长分支过程,简称为突变分支过程。
定义1[2]突变分支过程
状态空间E=Z+={0,1,2,…},其转移函数是P(t)={pij(t);i,j∈E=Z+}
并且满足Kolmogorov前向方程:P′(t)=P(t)Q
而其q-矩阵Q=(Qij;i,j∈E)定义为:

其中:a>0,d>0
定义2[3]常返性


引理1[2]C是一个相通类,设Q=(Qij;i,j∈E)在C上保守,则下面结论等价:
(1)C对于fij(t)是常返的;
(2)对于每一个a∈C,方程
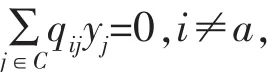
不存在非常数的有界解,j∈C。
引理2[3](Reuter,1957)假设{fn,n≥1},{gn,n≥1},{hn,n≥1}是非负数列,z0和z1是两个数,满足0≤z0<z1。定义数列{zn,n≥2}如下
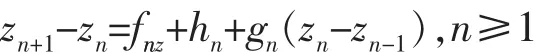
则数列{zn,n≥0}是有界的当且仅当

其中
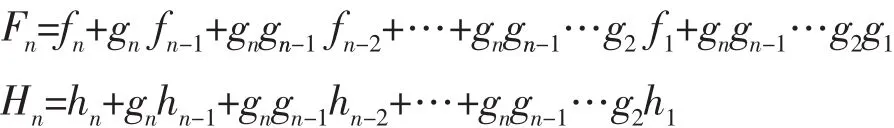
定理当d≥2a时,则Q=(Qij;i,j∈E)是常返的;
当d<2a时,则Q=(Qij;i,j∈E)是瞬时的。
由突变分支过程q-矩阵定义,i=1,噎,n,噎可表示为如下矩阵:

其中:当i<j-2时,qij=0

由引理2,{xn}有界当且仅当
当d=2a时,xn+1-xn=xn-xn-1,取{xn}=(0,0,…),方存在常数有界解,从而Q常返。
故当d<2a时,则Q=(Qij;i,j∈E)是瞬时的;当d≥2a时,则Q=(Qij;i,j∈E)是常返的。
[1]Chen An-yue,Zhang Han-jun,Existence,Uniquness,and Construction for Stochastically Monotone Q-Processes[J],Southeast Asian Bulletin ofMath,1999,23:559-583.
[2]邹杨,李扬荣,许安见.突变分支过程导出的积分半群及其性质[J]西南大学学报(自然科学版),2010.
[3]Anderson W.J.,Continuous-time Markov Chains[M],New York:Spring-Verlag,1991.

