浅谈转化与化归思想在解二面角中的运用

2011-01-26 06:29张瑛,雷丽

张瑛 ,雷丽

(商丘职业技术学院河南,商丘 476000)

一、空间维数的变化

“立体几何问题平面化”是解决立体几何问题的重要思想方法,二面角的求法也不例外。如“定义法 ”、“垂面法 ”、“三垂线法 ”、“射影面积法 ”等无不是这一思想方法的重要体现。

例 1：已知三条射线 SA、SB、SC所成的角∠ASB=45°,∠ASC=∠BSC=30°,求平面 ASC和平面BSC所成二面角的大小。

解：如图1,过 SC上任意一点 D,在平面 ASC内作 DE⊥SC交 SA于 E,在平面 BSC内作 DF⊥SC交 SB于 F,则∠EDF是二面角 A-SC-B的平面角,可证得△ESD≌△FSD。

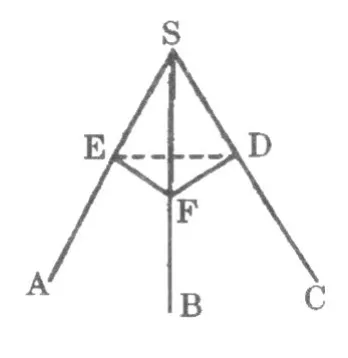
图1

在 △DEF中,有 EF2=

若所要求的二面角较难计算时,可退而求其次——即求出它的“邻补二面角”或“同位 (内错)二面角”的大小。

例 2：在长方体 ABCD-A′B′C′D′中 ,E为 AB的中点,AB=2BC,求二面角 A-D′E-C的大小。

解：如图2,连接 B′E、BC′,B′C

设 BC′与 B′C相交于 F,连接 BF。

∵BC′∥D′A ∴A、D′、E、F四点共面

∴二面角 A-D′EC的邻补二面角为 C′-D′E-C

在矩形 ABCD中,∵AE=EB=BC ∴DE⊥EC,又 D′D⊥平面 ABCD,∴D′E⊥EC同理 ,D′E⊥EB′ ∴D′E⊥平面 B′EC ∴D′E⊥EF ∴∠CEF为二面角 C′-D′E-C的平面角

∵EB⊥平面 BCB′,BF⊥B′C ∴EF⊥FC

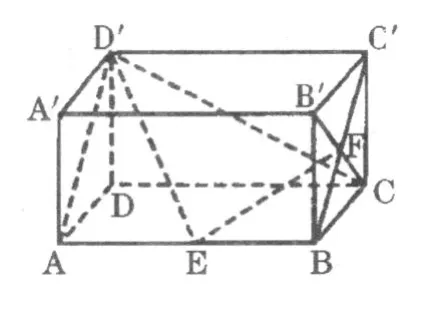
图2

∴∠CEF=30°

故二面角 A-D′E-C的大小为 150°(180°-30°)。

在求二面角时,有时可借助图形的几何特征将所求二面角转化为已知的折叠角公式或异面直线所成角来求,从而实现未知向已知的转化与过渡。

例 3：在正方体 AC1中,E、F分别是 C1B、AD1的中点,求二面角 E-BD-F的大小。

解：如图3,设正方体的棱长为 a,过 E作 EF⊥BD于 G,过 F作 FH⊥BD于 H,显然,BG=DH=

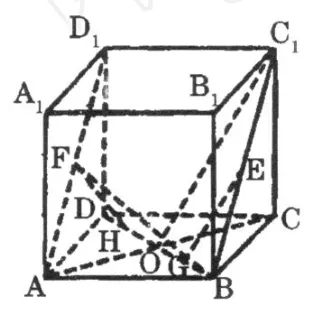
图3

设 AC∩BD=0,连接 OC1

∵AC⊥BD ∴C1O⊥BD

又 EG∥C1O ∴EG⊥

所以,HG为 EG、FH的公垂线段,二面角 EBD-F的大小等于异面直线 EG与 FH所成的角(或其补角)。设为θ,则由异面直线上两点间距离公式有

作为知识,向量与复数有许多地方是可以类比、相互贯通的,作为工具,向量比复数具有更灵活、更广阔的应用,而向量是数和形有机结合体,所以它在求二面体方面发挥了非凡的作用,为二面角的求法带来了新观点,增加了新色彩。

例 4：如图4,PA⊥平面 ABC,AC⊥BC,PA=AC=1,BC=,求二面角 A-PB-C的大小。

图4

解法一：取 PB的中点 D,连接CD,因为 PC=CB=,所以 CD⊥PB,作 AE⊥PB于 E,则二面有 A-PB-C的大小等于异面射线DC与 EA所成的角θ的大小。

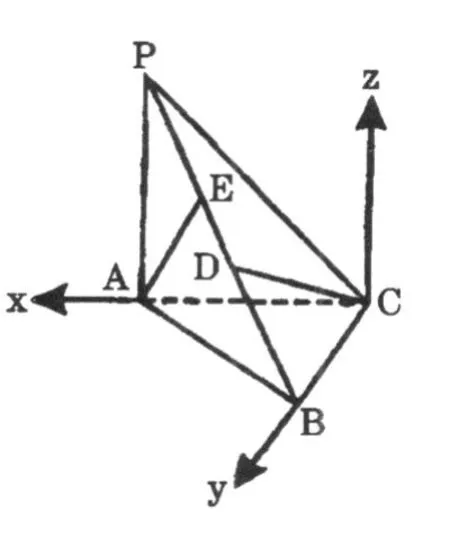
图5

解法二：如图5,建立空间直角坐标系 C-xyz,取PB的中点 D,连接 DC,可证DC ⊥PB,作 AE⊥PB,则向二面角A-PB-C的大小

解法三：如图6,作 CD⊥AB于 D,AE⊥PC于 E,易证 CD⊥平面 APB,AE⊥平面PBC

图6

如图,建立空间直角坐标系c-xyz

不难看出,转化与化归思想在二面角求法中发挥了重要作用。可以说,没有转化,就不可能求出任何一个二面角。总而言之,在数学教学中有意识地让学生去观察和思考问题,揭示教材的内在联系和层次性,善于运用化归转化的意识,找到正确的化归转化的方向和途径,就能提高学生的思维能力,提高学生的解题能力。

[1]张奠宙,宋乃庆.数学教育概论[M].北京：高等教育出版社,2009.

[2]王鲁欣.浅析高职高专经管类高等数学的改革[J].考试周刊,2009,(32).

[3]王峰.量化分析高职数学知识应用需求调查[J].职业技术教育,2010,(2).

[4]李志生,李东梅.理工科学生课外科技创新活动中创新能力培养的探索[J].高等教育研究,2007,(7).

[5]钱到翠.浅谈代数思维能力的培养[J].数学教育学报,1996,(2).