在频繁序列模式中挖掘并发序列模式

张 洋， 陈未如， 张立忠

(沈阳化工大学计算机科学与技术学院，辽宁沈阳110142)

序列模式挖掘是数据挖掘的一个重要研究内容，能够发现隐藏在大规模数据中的具有顺序关系的模式.结构关系模式挖掘是一种建立在序列模式挖掘基础上的新的挖掘任务，旨在寻找隐藏在序列模式后面的新的结构关系模式.结构关系模式［1－2］和序列模式一样在实际应用中也有重要的研究价值.结构关系模式和序列模式之间的关系如图1所示.

图1 结构关系模式和序列模式之间的关系Fig.1 The relationship between structural relation patterns and sequential patterns

图挖掘［3－5］、树挖掘［6－8］和偏序挖掘［9－11］与结构关系模式挖掘相似.从挖掘的对象上看，偏序挖掘和结构关系模式挖掘更为相似，结构关系可以看作是偏序关系的限定和扩展.结构关系中的并发关系、互斥关系和顺序关系可以看作是偏序关系的限定，他们简化了挖掘过程和挖掘结果.而结构关系中的重复关系、关联关系则不属于偏序关系，这使得结构关系模式挖掘在实际应用中更有价值.

经过几年的研究，本课题组建立了相对完整的结构关系模式挖掘理论体系，获得了一系列的研究成果.其中文献［12－13］分别从序列间相对关系角度和整个序列数据库的角度考虑序列模式之间的并发特性，提出了并发序列模式的定义、基本性质以及挖掘并发序列模式的算法.文献［14－15］提出了互斥关系模式的定义、性质和挖掘方法.文献［16］提出了重复关系模式的定义、性质和挖掘方法.本文依然从序列间的相对关系出发考虑序列模式间的并发性，对并发序列模式的性质进行描述，并利用并发序列模式的反单调特性及挖掘的非平凡特性，在文献［12］算法基础上对算法进行优化.通过实验对比可知:该算法在文献［12］算法基础上对挖掘结果进行了大幅精简，算法正确、有效.

1 基本概念

1.1 定义

设SDB={S1，S2，S3，…，Sn}是一个序列数据库，α与β为在某一最小支持度minsup下序列模式挖掘结果，且α与β互不包含.

定义1 若(α∠S)∧(β∠S)，则在序列s中α和β构成并发关系，表示为［α+β］S.一般地，如果(α1∠S)∧(α2∠S)∧…(αn∠S)，则相对于序列s，序列α1，α2，…，αn构成并发关系，表示为［α1+α2+…+αn］S，其中符号“∠”表示包含于.

定义2 序列α和β的并发度

序列模式α1，α2，…，αn的并发度可以定义为

这里Sk∈SDB，1≤k≤n，公式(1)中分子为同时包含α和β的序列的个数，分子为包含α或β的序列的个数;公式(2)同上.

定义3 设mincon为用户所给最小并发度阈值，如果concurrence(α，β)≥mincon［12］，那么α、β构成并发序列模式，表示成［α+β］.

示例:表1中因为〈ac〉和〈af〉都包含于S3=〈babfaec〉，所以，有［〈ac〉+〈af〉］〈babfaec〉.设客户给定最小并发度mincon为50%，在S3和S4中afac和bafc都满足并发关系，并且包含afac或bafc的序列个数为2，即 concurrence(〈afac〉，〈bafc〉)=100%≥mincon，所以，〈afac〉和〈bafc〉构成并发序列模式，表示为［〈afac〉+〈bafc〉］.

表1 示例序列数据库SDB和每个序列所支持的序列模式Table 1 A sample SDB and supported sequential patterns by each sequence

1.2 基本性质

性质1 ［x+y］=［y+x］

即并发序列模式满足交换律.

性质2 ［x+y+z］=［［x+y］+z］=

［x+［y+z］］.

性质2说明并发的各个序列之间满足可结合性.性质1和性质2保证了在挖掘并发序列模式过程中，任意挖掘次序都将会得到相同的结果.

性质3 并发关系与频繁项集、序列模式之间存在包含关系.在minsup≥mincon的情况下，一个频繁项集中的各个频繁项之间可构成并发模式，一个序列模式的各个元素之间以及各个子序列模式之间可构成并发模式.

例如，频繁项集(a，b)可以构成并发模式［a+b］，序列模式〈abc〉可以构成并发模式［a+ b+c］、［ab+ac+bc］等.由本性质所得到的并发模式并不是挖掘的目标.并发模式挖掘的结果应该是不包含在频繁项集或序列模式中的并发模式，即并发序列模式挖掘结果应具有非平凡特性.

性质4 多分支并发序列模式中去掉任意分支后仍构成并发序列模式，称为原并发序列模式的子模式.

性质4为并发序列模式的反单调特性，该性质可以用来指导采用自下向上的方法挖掘并发序列模式，在进行并发序列模式挖掘过程中将起到重要作用.

上述性质定理均可从定义出发进行推导证明，由于篇幅有限，此处略.

2 并发序列模式挖掘改进算法

任意序列模式之间的并发关系可以按定义1进行判断，利用定义2和定义3还可以判断满足并发关系的序列模式是否构成并发序列模式.但是对于一个序列数据库SDB，找到所有满足最小并发度的并发序列模式仍然是一个具有挑战的任务.

2.1 序列模式支持向量

每个序列模式spi(1≤i≤m)的支持向量如下:

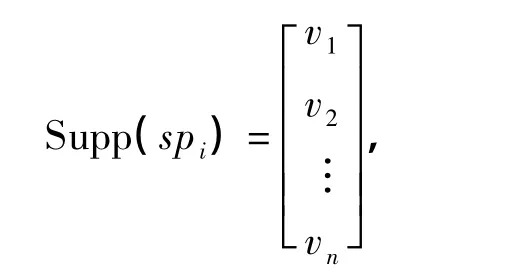
这里当spi(1≤i≤m)包含于Sk(1≤k≤n)，即spi∠Sk时，vk=1(1≤k≤n)，否则vk=0.

所有支持向量的集合构成支持矩阵Supp［SDB，SP］，矩阵中Sk(1≤k≤n)作为行，序列模式spi(1≤i≤m)作为列:

sp1 … spi … spm S1…Sk…Sn v11 … v1i … v1m·····vk1 … vki … v km·····vn1 … vni … v nm

当spi∠Sk(1≤k≤n，1≤i≤m)，即序列模式spi(1≤i≤m)包含于 Sk(1≤k≤n)时，Supp［Sk，spi］=vki=1;否则Supp［Sk，spi］=vki=0.

表1中序列数据库SDB对应的支持矩阵大致表示如下:

a b c e … abcc abfc afac bafc S1 S2 S3 S4 1000…00001111·10001111…01111110· 1111

同理［sp1，sp2，…，spk］表示k分支序列模式，它对应的支持向量可以表示为:

r1表示向量中值为“k”的元素个数，r2表示向量中不为零的元素的个数.

2.2 并发序列模式挖掘改进算法

INPUT:最小支持度 minsup，最小并发度mincon，序列数据库SDB.

OUTPUT:并发序列模式集Concurrent Sequential Patterns(CSPs).

METHOD:

(1)在用户指定的最小支持度minsup下对序列数据库SDB进行序列模式挖掘，SP={sp1，sp2，…，spm}为序列模式挖掘结果;

(2)对于任意spk∈SP and spk.length＞1 //spk.length表示spk中items的个数

{对于任意 spj∈SP and spj.length=spk.length-1

{如果spj∠spk将spj加入到spk.SubSeqs中}}

(3)按照2.1节支持矩阵的定义，求SP中每个序列模式的支持向量Supp(spi)，得到支持矩阵Supp［SDB，SP］;

(4)基于支持矩阵Supp［SDB，SP］，根据

2.1 节相关定义

对于任意spi∈SP

对于任意spj∈SP

如果┐(spi∈SubSeq(spj))∧┐(spj∈Sub-Seq(spi))值为真//spi和spj不互相包含

计算spi和spj的相对并发度

如果concurrence(spi，spj)≥mincon

CSPs=CSPs∪［spi+spj］

(5)根据并发序列模式的反单调特性，循环通过spi(1≤i≤m)及(k－1)-分支并发序列模式构造k-分支并发序列模式(k≥3)，找出满足mincon的并发序列模式，将其加入CSPs中，具体方法如下:

对于任意spi∈SP

对于任意(k－1)-CSP∈CSPs//(k－1)-CSP表示任意(k－1)-分支并发序列模式

{对于构成(k－1)-CSP的任意序列模式spj如果┐(spi∈SubSeq(spj))∧┐(spj∈SubSeq(spi))为真

计算spi和(k－1)-CSP的相对并发度

如果 concurrence(spi，(k－1)-CSP)≥mincon

CSPs=CSPs∪［spi+(k－1)-CSP］//新得到的k分支并发序列加入结果集

(6)重复步骤(4)，直到不能产生新的模式为止;

(7)输出结果集CSPs.

算法中步骤(2)求得每个spk∈SP对应的直接子序列集，从而得到所有序列模式的直接子序列集SubSeqs.步骤(4)、步骤(5)中条件┐(spi∈SubSeq(spj))∧┐(spj∈SubSeq(spi))是为了确保spi、spi的直接子序列集SubSeq(spi)及Sub-Seq(spi)中每个元素的直接子序列集 SubSeq (SubSeq(spi))不包含spj;同理spj、spj的直接子序列集SubSeq(spj)及SubSeq(spj)中每个元素的直接子序列集SubSeq(SubSeq(spj))不包含spi，在算法实现时此处应用递归调用来完成.

现有算法通过序列模式的支持向量产生了所有可能的k(k≥2)分支并发序列模式，没有考虑到构成并发序列的各序列模式之间的相互包含关系，导致挖掘结果中存在大量冗余的平凡并发模式.本算法求得序列模式挖掘结果集中每个序列对应的直接子序列SubSeqs，递归利用Sub-Seqs及SubSeqs中每个序列的直接子序列集检测序列之间的包含关系，对挖掘结果进行了大幅精简.现有算法通过产生(k－1)分支序列模式的支持向量生成k分支并发序列，产生了大量的中间数据.本算法直接利用支持矩阵产生k分支序列模式的支持向量来计算并发度，生成k分支并发序列模式，避免了大规模中间数据的产生，提高了算法执行效率.

3 实验验证

对本算法进行实验验证.最小支持度minsup=50%，最小并发度mincon=90%.SDB如表2所示，本算法与现有算法挖掘结果对比如图2所示.

表2 实验SDBTable 2 SDB in experiment

图2 挖掘结果对比图Fig.2 Mining results contrast diagram

从图2可以看出:本算法和现有算法挖掘得到的曲线图数据走势相似，挖得的并发序列模式的数目随着并发分支数的增大都呈现数倍增大，当分支数到达某一数值后，并发序列模式数又呈现数倍减少现象.从图2还可以看出:根据并发序列模式的反单调特性，本文算法利用(k－1)-分支并发序列模式和频繁序列模式spi生成k-分支并发序列模式，避免了冗余k-分支序列的产生;另外在计算并发度之前，递归利用直接子序列集Subseqs判断序列模式之间是否存在包含关系，从而对挖掘结果又进行了大幅精简，避免了存在相互包含关系的序列构成的并发序列在挖掘结果中的出现，也因此使得本文算法挖掘得到的并发分支数及其对应的并发序列模式数都比现有算法有了大幅的减少，从而使挖掘结果更有实际意义.

4 结论

结构关系模式挖掘是本课题组新提出的一种数据挖掘理论，并发序列模式挖掘是结构关系模式挖掘的一个重要分支.本文从并发关系、并发度角度给出了并发序列模式的定义、性质，并提出了并发序列模式挖掘的改进算法，实验证明算法正确、有效.在生物信息领域研究中，DNA序列之间关系的确定主要靠实验方法，实验方法费时、费力、成本高，另外实验方法还受生物体本身的限制.将结构关系模式挖掘理论应用于DNA序列间关系的分析，对开拓新的生物信息分析方法，降低生物实验成本将有重要的意义，这将是本课题组下一步的研究工作.

［1］ CHEN Weiru，ZHANG Yang，CHEN Shanshan，et al.From Sequential Pattterns to Structural Relation Patterns［C］//Li Keqiu，Min Geyong，Zhu Yongxin et al.Proceedings of IEEE International Conference on Scalable Computing and Communications-The 8th Internation Conference on Embedded Computing，ScalCom-EmbeddedCom 2009.Dalian:IEEE Computer Society，2009:148－153.

［2］ CHEN Weiru，CHEN Shanshan，ZHANG Yang.Structural Relation Sequential Pattern Mining［C］// TIAN Xianzhi，ZHU Egui.Proceedings of ICRCCS 2009-2009 International Conference on Research Challenges in Computer Science.Shanghai:IEEE Computer Society，2009:41－44.

［3］ Kuramochi M，Karypis G.GREW:A Scalable Frequent Subgraph Discovery Algorithm［C］//Proceedings of the 2004 IEEE International Conference on Mining(ICDM'04).Brighton:ICDM，2004: 439－442.

［4］ Vanetik N，Gudes E，Shimony S E.Computing Frequent Graph Patterns from Semi-structured Data［C］//ICDM'02 Proceedings of the 2002 IEEE International Conference on Data Mining.Washington:IEEE Computer Society，2002:458－563.

［5］ Huan J，Wang W，Prins J，et al.SPIN:Mining Maximal Frequent Subgraphs from Graph Databases［C］//KDD'04 Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM， 2004:581－586.

［6］ Asai T，Abe K，Kawasoe S，et al.Efficient Substructure Discovery from Large Semi-structured Data［C］//Proceedings of the 2nd SIAM International Conference on Data Mining.Arlington:SIAM，2002:158－174.

［7］ Zaki M J.Efficiently Mining Frequent Trees in a Forest［C］//Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM，2002:71－80.

［8］ Ruckert U，Kramer S.Frequent Free Tree Discovery in Graph Data［C］//Proceedings of 2004 ACM Symposium on Applied Computing.Nicosia:ACM，2004:564－570.

［9］ PEI Jian，LIU Jian，WANG Haixun，et al.Efficiently Mining Frequent Closed Partial Orders［C］//ICDM'05 Proceedings of the fifth IEEE International Conference on Data Mining.Washington:［s.n.］，2005:753－756.

［10］Casas-Garriga G.Summarizing Sequential Data with Closed Partial Orders［C］//Proceedings of the Fifth SIAM International Conference on Data Mining.Newport Beach:SIAM，2005:380－391.

［11］DONG Guozhu，PEI Jian.Mining Partial Orders from Sequences［J］.SEQUENCE DATA MINING Advances in Database Systems，2007，33(10):89－112.

［12］张洋，陈未如，陈姗姗.并发序列模式挖掘算法研究［J］.计算机应用，2009，29(11):3096－3099.

［13］LU Jing，Osei Adjei，CHEN Weiru，et al.An Apriori-based Algorithm for Mining Concurrent Branch Pattern［C］//Proceeding of the 4th RoEduNet International Conference:Education/Training and Information/Communication Technologies-RoEduNet 2005.Romania:RoEduNet，2005:183－189.

［14］张洋，陈未如，纪元.互斥关系模式挖掘算法研究［J］.计算机工程与设计，2008，29(22):5776－5779.

［15］CHEN Weiru，LU Jing，Malcolm Keech.Discovering Exclusive Patterns in Frequent Sequences［J］.Int.J.Data Mining，Modeling and Management，2010，2 (3):252－267.

［16］彭弗楠，陈未如，黄宁.结构关系模式挖掘中的重复序列模式挖掘［J］.甘肃科技，2008，24(8):20－22.