分块DPCM与5/3整数小波变换结合的天文图像无损压缩*

朱贵富，邓 辉，王 锋，季凯帆

(昆明理工大学云南省计算机技术应用重点实验室，云南 昆明 650051)

随着技术的发展，海量的图像数据与有限的存储空间、有限的网络带宽之间的矛盾日趋突出。在诸如医学、遥感、天文图像的存储传输等应用场合，无损压缩方法是保证数据无失真且节约存储空间的唯一方法。经典的无损压缩方法［1］主要包括霍夫曼编码、算术编码、基于字典的LZW、位平面编码、行程编码等，它们作为数据压缩的通用方法，并没有考虑图像数据本身的特点，图像压缩率很低，难于满足现在图像处理的要求。目前对图像无损压缩的研究大多集中在如何有效去除像素间相关性上，具体可以分为基于预测的方法、基于整数变换的方法、基于矢量量化的方法，或者多种方法结合使用的综合方法［2－7］。

小波变换是一种同时兼顾频率域和空间域定位的变换，近二十年来，小波变换在理论研究和工程应用方面都得到了迅速发展。在第一代小波变换中，由于变换系数是浮点型的，对变换系数进行编码时需要进行量化取整运算，从而产生精度误差，因此不能用于图像的无损压缩。Sweldens［8］提出的提升方案(Lifting Scheme)是目前构造第二代小波较为有效的方法，利用提升方案经过适当的提升步骤可以实现真正的可逆整数小波变换，Daubeches等人［9］深入阐述了可逆双正交小波变换理论，给图像的无损压缩提供了理论基础，使得小波变换在图像无损压缩领域得到很大发展。新一代静止图像压缩标准JPEG2000采用基于整数的5/3滤波器实现无损压缩［10］;田金文等人［2］利用整数Haar小波结合分块DPCM实现了图像无损压缩，但是由于Haar小波去冗余能力较弱［3］，因此其压缩比不太理想;赵丽红［4］、吴冬梅［5］等人分别根据医学图像和超光谱图像的特点采用将DPCM与整数小波结合的方法实现无损压缩，提高了压缩比，但是他们的方法需要一次性加载整张图片，对于超大图片(例如8k×8k或更大)的情况，存在预测误差扩散和占用系统资源过高的问题。

在实际天文应用中，天文图像的无损压缩一般采用现成软件［6］(如WinRar、WinZip、PKZip、tar工具)实现。栗志等人［7］用传统的数据压缩方法对天文图像进行了压缩性能分析对比;胡新华等人［11］，W D Pence等人［12］分别用各种流行的压缩软件测试了FITS格式数据的无损压缩情况，其压缩比为1～3，效果不甚理想。李龙等人［6］采用嵌入零树编码改进方案实现天文图像的有损和无损压缩，但是嵌入零树编码用于无损压缩时的运算过于复杂，不利于硬件实现。

综上所述，无损压缩方法已经被广泛地应用于各个领域，但均存在一定的不足。为了有效解决天文图像无损压缩问题，解决如丽江2.4 m望远镜和澄江红外太阳塔等数据远程实时传输等要求，本文以夜间可见光观测图像为基础，提出一种无损压缩方法，希望提高压缩比与压缩性能，无疑是有意义的。

1 相关研究

1.1 DPCM预测模型

差分脉冲调制［1］(Differential Pulse Code Modulation，DPCM)预测基本思想是通过对像素实际值和预测值之间的预测误差进行提取和编码，来消除在空间上较为接近像素之间的冗余信息。为了实现预测的可逆性，需要对预测结果进行取整。容易得到预测公式:

其中X'(n)是预测器根据预测策略进行预测后取整的结果。显然，预测还原时遵循:

图像数据采用二维数组表示，因此对图像的预测为二维预测。一种常用的图像预测器为:

(3)式中D、B、C均为n的前像素，n在图像二维数组中的位置为n(x，y)，D、B、C分别为:D(x－1，y)、B(x，y－1)、C(x+1，y－1)。预测的边界处理为:当缺少B、C时候(即第一行)则变为X'(n)=D;当缺少D时候，变为X'(n)=int［(3B+C)/2］;当缺少C时候，变为X'(n)=int［(D+B)/2］;B、C、D均缺少则为第一个像素，不预测。

1.2 5/3整数小波变换

Sweldens等人［8］提出的一种新的小波构造方法，经过适当步骤可以实现可逆整数小波变换(Reversible Integer-To-Integer Wavelet Transform，RITIWT)，使得小波变换可以应用于无损压缩领域。提升方案(Lifting Scheme)继承了第一代小波变换的多分辨特性，放弃了平移和升缩，对于信号的分解直接通过分裂、预测、更新3个基本运算构成。该提升方案的3个步骤如下:

(1)分裂(Split):将信号Si分裂成为两个互不相交的子集c2i和c2i+1，即奇偶分开;

(2)预测(Predict):采用某种准则(例如最小均方差)，用奇预测偶，或者偶预测奇;

(3)更新(Update):理想状态是第2步的预测均方差为0，但是实际上不太可能正好为0，因此需要更新，使得均方差尽可能小。

由提升方案可构造出5/3整数小波变换，其正变换和逆变换为:

在构造出完全可逆的变换之后，可以采用熵编码器对变换系数进行编码。

2 基于DPCM与RITIWT的天文图像分块无损压缩

经分析，不难得出如下理论推论，由于DPCM对预测结果进行了取整使得其预测结果可逆;而RITIWT实现的是整数到整数的小波变换，亦是可逆的;因此采用DPCM与RITIWT在理论上是可以实现天文图像无损压缩的。通过对原始图像的分块，不需要加载整张图像，使得该算法最少只占用一个图像分块加一些系统开销的资源;通过DPCM预测变换，去除了象素间大部分冗余;再经过5/3整数小波变换，分开高频和低频分量，使得图像能量进一步集中，图像数据形式更加紧凑，最后通过霍夫曼算法对小波变换的系数进行编码，理论上会比单种压缩方法效果更好，且其中涉及的DPCM预测、5/3整数小波变换、霍夫曼编码算法实现均较为简单，利于硬件实现。

2.1 压缩框架与流程

图1 基于DPCM与RITIWT的天文图像分块无损压缩流程Fig.1 Framework of segmention-based lossless compression of an astronomical image using the DPCM and RITIWT

压缩的基本框架如图1，压缩编码具体步骤为:

Ⅰ:读入原始FITS图像;

Ⅱ:将图像分成n×n的子块;

Ⅲ:对每一个子块，以子块的第一个像素为基准进行DPCM预测 (第一个像素不预测);

Ⅳ:对每一个子块的预测结果进行5/3整数小波变换;

Ⅴ:对每一个子块的变换系数采用霍夫曼编码;

Ⅵ:顺序合并每一个子块的编码结果，对每个子块添加简单标志位，组成压缩后的数据。解压过程为压缩编码的逆过程。

2.2 天文图像分块

DPCM的预测会扩散误差，有时候对压缩性能的影响可能是巨大的，图像越大，扩散误差越多。天文图像一般很大，如果不采取某些减小误差措施，对天文图像的预测可能效果并不理想。一种有效的解决方案就是对大图像进行分块，把原图像分成较小的若干块，分别进行预测，从而将误差控制在一个块内，有利于远程传输。

另一方面，通过分块，该算法压缩时候不需要一次就加载整张图片到内存中，比不使用分块的方法大大节省了内存。此外由于采用分块技术，利于实现并行处理，对于某些实时性要求高的场合，是个较好的解决方案。

分块太大，分块的效果不明显;分块太小，则造成循环分块的系统开销增加。实际应用中，可以做成一个参数的形式，与用户交互而定。本文中，考虑到FITS格式的特点，采用8×8分块方法。

2.3 压缩参数选择

压缩过程中，首先对图像分块，然后DPCM预测和整数小波变换，最后编码。这里涉及DPCM预测策略、整数小波变换的小波基选取和边界处理等问题，需要选定这些参数。

(1)DPCM的预测策略:DPCM的缺点是当某个像素与同一组像素之间的差异较大时，会扩大预测误差，同时将扩大的误差一直扩散，严重影响压缩性能。因此，DPCM的关键是预测策略的选择，预测策略的好坏直接决定压缩性能的好坏，而这个策略通常和图像的统计特性有关。本文通过实验，选择了公式(3)作为天文图像的预测策略。

(2)小波基的选取:不同的小波基具有不同的时频特征，用不同的小波基分析同一张图像会产生不同的结果，因此必须选取一个合适的小波函数。从公式(4)、(5)可以看出，5/3整数小波只有整数的加法和移位运算，变换过程中不会产生浮点，实现真正的变换无损，且方便硬件实现，本文参考JPEG2000中无损压缩采用的5/3小波作为小波基，小波变换的边界延拓采用对称延拓方式。

3 实验及分析

根据以上压缩框架和具体步骤，使用VC++6.0在微机上实现了上述算法原型，对云南天文台1 m望远镜所拍摄到的S1203_V_001_1_0000.FITS～S1203_V_005_1_0000.FITS共5张图进行了实验(见图2)。这些图像像素均为2048×2048，图2(a)、(d)对亮度做了适当拉升使得其关键数据调整到可显示的范围，图2(b)、(c)图像数据较为复杂，图2(e)相对简单。

图2 实验中用到的测试图像Fig.2 Test images in our experiments

程序中对FITS图像的读写采用官方标准库函数;图像分成8×8的子块;DPCM预测策略采用公式(3)的方法;小波变换采用5/3整数小波变换(即公式(4))对图像进行3级分解，边界处理方式为对称延拓;变换系数熵编码器采用霍夫曼编码。

本文算法的关键是通过可逆的DPCM预测和整数小波变换，降低变换后图像的信息熵，从而使得熵编码理论上可以实现更高的压缩比，表1给出了测试图像变换前后的信息熵。

表1 测试图像变换前后的信息熵Table 1 Information entropies of test images before and after the wavelet transformation

为了验证算法的有效性，还单独使用DPCM预测和整数小波变换来结合霍夫曼编码进行压缩，同时还与Windows下WinRar、WinZip、PKZip和Linux下tar工具的压缩结果进行了对比。各种无损压缩方法的压缩比参见表2，本文方法与传统软件的压缩比结果参见表3，各种无损压缩方法的压缩和解压时间参见表4，本文方法与传统软件压缩和解压时间参见表5。

表2 单种方法与组合方法压缩比Table2 Compression ratios of single methods and combination methods

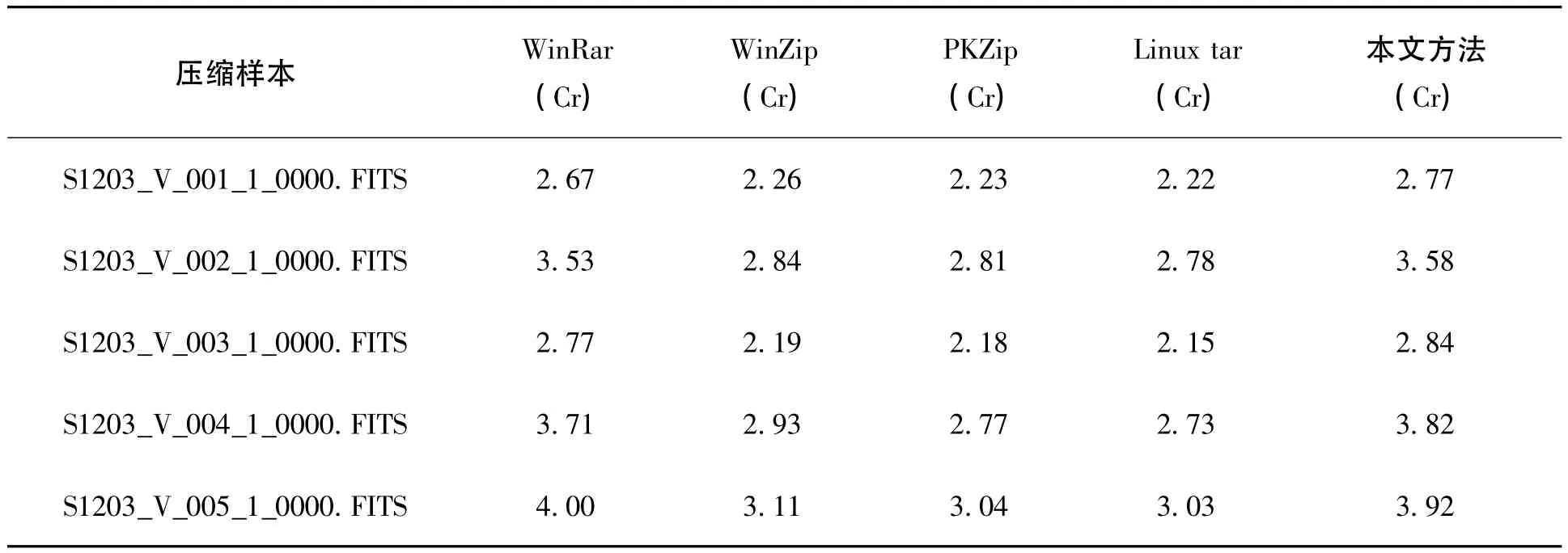
表3 本文方法与传统软件压缩比Table 3 Compression ratios of our method and commonly used softwares

表2，表3中Cr=压缩前图像大小/压缩后图像大小，由于采用了无损压缩方案，表2中4种压缩方法的均方误差(MSE)都为0。

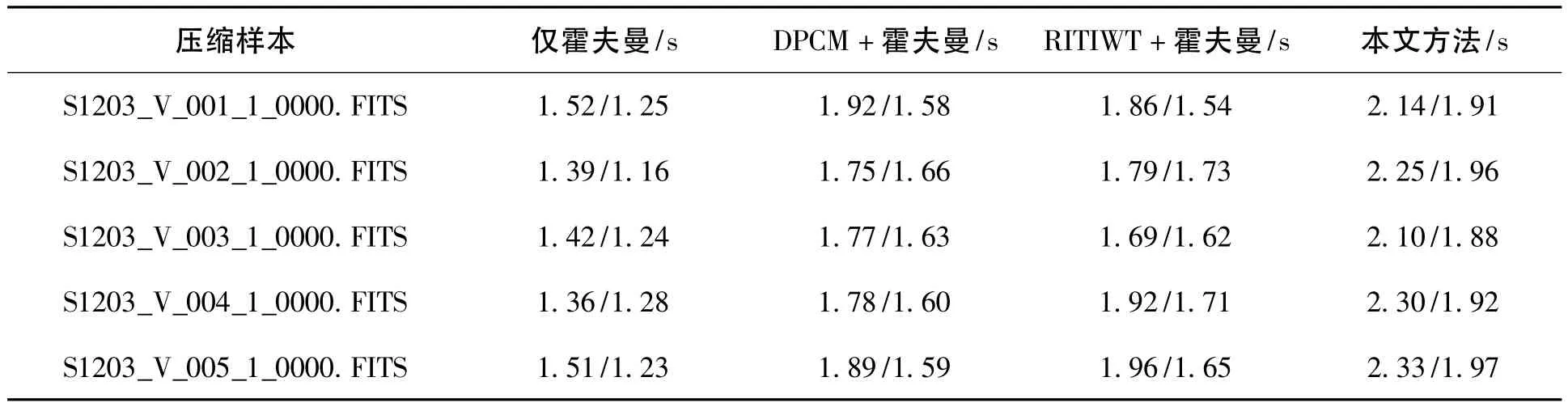
表4 单种方法与组合方法平均耗时(压缩/解压)Table 4 Average times for encoding/decoding in single methods and combination methods

表5 本文方法与传统软件平均耗时(压缩/解压)Table 5 Average times for encoding/decoding in our method and commonly used softwares

表4、表5中单位为s，运行平台为:一个Pentium(R)42.40 GHz CPU，2048 MB内存，Windows Server2003操作系统，其中表5中tar的测试为Linux操作系统。由于操作系统运行多任务的原因，每次压缩和解压的实际时间和表4、表5略有误差，表4和表5给出的是10次测试的平均时间。

无损压缩的理论极限是信息熵，仅使用熵编码压缩不可能有太大的提高，通过对原始图像进行可逆变换，使得变换后的信息熵小于原图像信息熵，才能提高压缩比，从表1可以看出，通过变换后的数据信息熵远远小于原图信息熵，从而理论上可能提高压缩比。从表2可以看出，仅使用霍夫曼编码的压缩比很低;预测编码通过仅对预测误差编码从而可以较明显地提高压缩比;基于整数小波变换的方法由于小波变换将高低能量分开也明显提高了压缩比;而本文提出的综合前三种方法应用于天文图像确有明显的提高。压缩速度方面，通过表4可以看出，本文方法比单独使用DPCM预测编码和IWT编码的时间稍多一些，但其压缩比确有明显的提高。通过表3和表5表明，本文方法比常用的tar、PKZip、WinZip、WinRar平均压缩比分别提高了30%、29%、26%、2%左右，同时耗时远小于WinZip和WinRar，耗时略多于PKZip和tar但大大提高了压缩比，实验过程中WinZip和WinRar均选择最高压缩比进行的压缩。

表3中最后一组测试数据本文方法比WinRar效果稍差，由于本文的预测策略，并不一定是最佳预测策略，该结果可能是误差累积传递而导致的，寻找更合理的预测策略是未来可以继续完善的方向。另外，本文中提到的对超大天文图像进行分块，利于并行处理，如果能实现在集群上由各子节点对分块图像进行压缩，将大大降低压缩时间;或者采用多块专用芯片并行对各个分块图形进行处理，既能节约成本，又能满足实时性要求。

4 结论

本文探讨了一种将分块DPCM与可逆整数小波变换相结合应用于天文图像的无损压缩方法，并对此方法的原理和实现做了分析与介绍。通过对比实验验证，本文的方法比仅用整数小波变换或预测编码都有明显的提高;比在天文图像存储时常用的tar工具、PKZip、WinZip、WinRar软件在压缩比上分别提高了30%、29%、26%、2%左右;压缩速度远大于WinZip和WinRar，可以在一定程度上减少海量天文图像存储空间和远端传送的等待时间。由于对图像进行了分块，利于并行处理，对于实时性要求高的应用场合，可以首先采用分块，然后再进行压缩处理。对于预测策略的选取，考虑到压缩速度，本文测试中采用的策略可能并不是最佳的预测，寻找更加合理的预测策略，可以进一步提高压缩比。

［1］Rafael C Gonzalez，Richard E Woods.冈萨雷斯数字图像处理(第二版)［M］.阮秋琦，阮宇智，译.北京:电子工业出版社，2003.

［2］田金文，柳斌，柳健.用整数Haar小波变换和分块DPCM实现静止图像数据的信息熵保持型压缩编码［J］.通信学报，2000，21(11):29－34.Tian Jinwen，Liu Bin，Liu Jian.The Information Entropy Preserved Coder of Still Image by Integer Haar Wavelet Transforms and Subblock DPCM［J］.Journal of China Institute of Communications，2000，21(11):29 －34.

［3］肖江，吴成柯，李云松，等.多光谱图像的3D EBCOT压缩编码算法［J］.西安电子科技大学学报(自然科学版)，2005，32(4):549－554.Xiao Jiang，Wu ChengKe，Li YunSong，Xiang LiBin，Yang JianFeng.Compression of the Multispectral Image by the Three-dimensional EBCOT Coding Algorithm［J］.Journal of Xidian University，2005，32(4):549 －554.

［4］赵丽红，天亚男，沙永刚，等.DPCM与小波变换结合的医学图像无损压缩［J］.东北大学学报(自然科学版)，2007，28(10):1454－1457.Zhao Lihong，Tian Yanan，Sha Yonggang，et al.Lossless Compression of Medical Images by Combining Integer Wavelet Transform with DPCM［J］.Journal of Northeastern University(Natural Science)，2007，28(10):1454－1457.

［5］吴东梅，王军，张海宁.基于谱间DPCM和整数小波变换的超光谱图像无损压缩［J］.光子学报，2008，37(1):156－159.Wu Dongmei， WangJun， ZhangHaining. Research of Hyper-spectral Image Lossless Compressing Technology Based on DPCM Between Spectra and IWT［J］.Acta Photonica Sinica，2008，37(1):156－159.

［6］李龙，代红兵，许骏.基于小波变换的图像压缩在天文远程观测中的应用研究［J］.天文研究与技术——国家天文台台刊，2008，5(4):380－395.Li Long，Dai Hongbing，Xu Jun.The Study of the Application of Image Compression Based on Wavelet Transformation in Astronomical Remote Observation［J］.Astronomical Research ＆Technology——Publications of National Astronomical Observatories of China，2008，5(4):380－385.

［7］栗志，周卫红.数字图像压缩方式在天文上的应用［J］.天文学进展，1996，14(3):259－261.Li Zhi， Zhou Weihong.The Application of the Ditigal Image Compression Technique to Astronomy［J］.Progress in Astronomy，1996，14(3):259 －261.

［8］Sweldens.The lifting scheme:Acustom—design construction of biorthogonal wavelets［J］.Applied and Computational Harmonic Analysis，1996，(3):186 －200.

［9］Daubeches I，Sweldens W.Factoring Wavelet Transforms into Lifting Steps［J］.J Fourier Anal Appl，1998，3(4):247 －269.

［10］ISO/IEC.ISOIEC 15444 －1:Information Technology-JPEG2000 Image Coding System-Part 1:Core Coding System［S］.

［11］胡新华，邓元勇，王先平.FITS图像处理技术荟萃及在太阳观测中的应用［J］.天文研究与技术——国家天文台台刊，2008，5(1):55－65.Hu Xinhua，Deng Yuanyong，Wang Xianping.Collection of Techniques on Dealing with Image Files of FITS Format and Applications to the Solar Observation［J］.Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2008，5(1):55－65.

［12］W D Pence，R Seaman，R L White.Lossless Astronomical Image Compression and the Effects of Random Noise［J］.Publications of the Astronomical Society of the Pacific，2009，121:414－427.