基于有效点扩散函数的高精度测光*

王 娴，苏成悦，王婷婷

(广东工业大学物理与光电工程学院，广东 广州 510006)

照相天体测量学中一种常见的工作是星像的中心位置和光度的精确测量。光度测量指测量来自天体的有限波段范围内的辐射流，简称测光，常以星等表示。随着测光方法的日益完善和研究的逐步深入，光度测量成为研究各类天体物理性质的重要方法。测光依据的基本原理是在相同条件下，等同的辐射流能使探测器产生同样的响应。根据这一原理，将待测星和已知星等的星作比较，从探测器对它们的响应便可推算出待测星的星等或星等变化。比较星是事先已经确定星等的定标星，或参照定标星精确测定了星等的标准星，即相对测光。将待测星的光谱和实验室中的绝对黑体比较，测出天体亮度，即绝对测光。

目前测光的主要方法有孔径测光和点扩散函数拟合测光［1－4］。在传统的处理方法如DAOPHOT(Stetson 1987)中使用 Gauss函数［5］、Kenneth J Mighell使用了 Matphot函数［6］，把一个函数正确地放置在一颗星像上，对这个函数在星像范围内每个像素所占的面积积分，取其积分结果和该像素观测流量值之差，以此达到最接近的拟合，从而建立起所采用的点扩散函数。Anderson等人提出了有效点扩散函数(effective Point Spread Function，ePSF)拟合测量星体中心［7－8］，利用他们的方法，本文对2007年10月12日在国家天文台1 m地平式反射望远镜观测的16幅CCD图像资料进行测光，得到了满意的结果。利用ePSF拟合测光，需要两个基本的步骤:首先对其进行求解，再利用它拟合星像得到光度信息。

本文分为4部分，第1部分介绍ePSF的求解过程，第2部分介绍利用ePSF拟合星像得到星体的光度信息，第3部分给出测量结果，最后对测量结果做了比较和讨论。

1 有效点扩散函数的求解

对光学系统，输入为点光源时其输出像的光场分布称为PSF(仪器PSF)，即光学系统的脉冲响应函数。本文采用的图像资料中所有的星体都可看作点光源。由于仪器PSF的隐含特性，可经过变换得到各量之间的关系［6］。其中，x*、y*是星像的中心位置，pij为星像在(i，j)位置处的灰度值，f*表示通量(即星体的光度信息)，ψE(i－x*，j－y*)为ePSF，简写为ψEij，s*是天光背景。

可以认为一幅星图中所有星像归一化后的ψEij相同［6］，每个星像可以看作ePSF在星像位置处的一个采样。而星像的每个像素点可以看成是ePSF的一个采样点。一般情况下，星像的中心不会恰好在像素的中心。如图1，图中“○”代表星像中心，“*”代表像素中心。一幅星图中有上百个星像，每个星像又由许多采样点构成，因此可以从这许多采样点中通过迭代得到ePSF。

图1 ○代表星像中心 *代表像素中心图Fig.1 Pixels surrounding a stellar image(with the center marked by“○”)

图2 采样点示意图Fig.2 Illustration of image points(asterisks)where an ePSF is sampled

通过数值的方法列出ePSF在每个采样点的值，即其在图2中标记“*”处的值。为了使求得的ePSF更连续、平滑，利用样条插值的方法在像素间插入了3个采样点。具体步骤如下:

(1)选择星像，选择信噪比大的星像，即亮星，本文选择了灰度值大于3倍背景值的星像，并剔除饱和星。所选星像如图3中标记1～38的星像(图示为原图的负值图像)。在本文所处理的图像资料中，星像中心位置及光度信息包含在31×31的像素区域内，因此提取ePSF时选择了31×31的像素区域。并逐个检查所选星像区域有无其他星像，若有则剔除该星像，不作为提取ePSF的被选星。

(2)根据(1)式可得到(2)式，利用(2)式求得ψEij。由(2)式可看出，要计算ψEij需要天光背景、星像中心位置及通量的初始信息。对于天光背景，本文采用Da Costa等人计算天光背景的方法［9］。中心及通量信息可通过高斯拟合得到［10－11］。

图3 星图(星像附近的数字为ePSF样本星的编号)Fig.3 Marks for stellar images(the numbers are for those used to sample our ePSF)

(3)在两个ψEij采样点间通过样条插值插入3个采样点。对于每个星像，可得到121×121个采样点，共38颗星。接下来的工作就是从这121×121×38个采样点中提取ePSF信息。即计算其在对应格点(图2中标记*的点)的值。将所有星像的ψEij中心位置重合，如图2(示意图，只画了星像中心5×5像素区域)，图中小圆点代表每个采样点。

(4)从这些采样点中减去当前ePSF模型得到残差，第一次该模型是0，残差即采样点本身。

(5)计算每个格点的值时，在以该点为中心△x、△y均为0.25个像素的矩形范围内，计算残差平均值及标准偏差δ，去除比平均值大2.5δ的那些采样点，剩余采样点的平均值作为ePSF模型在该格点的采样值。为使其更连续平滑，再用5×5的均值滤波模板平滑格点值。图4是均值滤波前ePSF模型的等高线图。图5是均值滤波后的。从图中可看出，滤波后的等高线图更平滑，特别是中心位置处的。

图4 滤波前ePSF等高线图Fig.4 Contour map of the ePSF before filtering

图5 滤波后ePSF等高线图Fig.5 Contour map of the ePSF after filtering

(6)这样得到的ePSF模型并不一定关于中心对称，可以在中心10×10区域范围内用如(3)式所示的二次抛物面拟合采样点［8］，求出偏差x0、y0。如果该模型关于中心点对称，则x0、y0均为0。否则将其平移x0、y0，可以利用样条插值的方法计算ePSF对应格点的值。

(7)返回步骤(4)，迭代至5次退出循环。即得到ePSF模型。图6为所求模型的三维表面图，图7为ePSF在△y=0处的切线图。从图中可看出它关于△x=0很好地对称。类似的，在△y=0处有相同的切线。

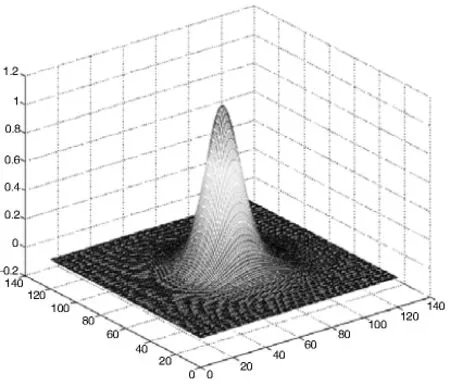
图6 有效ePSF模型的三维表面图Fig.6 The 3-dimensional illustration of the model of the ePSF

图7 有效ePSF模型在处的切线图Fig.7 The model of the ePSF at△y=0

2 用有效点扩散函数拟合星像

得到ePSF后，就可利用它来拟合星像，进行光度测量。本文测量了灰度值高于1.3倍背景值的星像，如图3中标记“○”的星像。可通过迭代找到合适的参数x*、y*、f*使得(4)式的值最小。如文献［6］4.3节所描述的，参数f*在等式中线性出现，因此求解f*时可以将参数x*、y*看作常数，f*作为变量对上式求导并令导数为0，即可求得f*如(5)式所示;而ψEij跟参数x*、y*之间的关系是非线性的，因此需要将上式在ψEij的0点附近一阶泰勒展开，再利用最小二乘法求得δx*如(6)式所示［12］，并且，δy*及y*有类似的表达式。式中 AP为拟合的星像区域 (Array of Pixels)。该区域不能过大也不能太小，远离星像中心的区域由于噪声的原因信噪比大幅度降低，但又要尽可能多的包含星点信息。从图7可以看出，由于ψEij的信息包含在≤10的区域内，因此选择≤10与≤10的区域测量光度，即ePSF中心21×21的矩形区域。

式(6)中 qij=1/pij，Rij=pij－s*－f*ψEij。迭代退出条件为＜0.001，且＜0.001。

3 测量结果

本文对国家天文台兴隆观测站1 m地平式反射望远镜观测星团NGC2168的16幅CCD图像进行资料分析。希望通过深入探讨测光方法，提高测光精度。望远镜和CCD的有关参数见表1。采用相对测光，比较星一般选择星图中比较亮且孤立的星，但又不能选择太亮的星，以免出现计数溢出的情况，即饱和星。综合考虑选取标记为21的星作为比较星fm。星的亮度通常用星等来表示:

表1 天文望远镜和CCD的参数说明Table 1 The parameters of the telescope and CCD camera used by us

假设第i幅图像中第j颗星的星等为mij，然后在多幅图像中统计它们的平均值mj及标准偏差 σj，用σj来衡量测量的内部精度。测量精度如图8，图中标记“○”的为利用Gauss函数拟合测量所得结果，标记“●”的为利用ePSF拟合测量所得结果，从图中可以看出，本文方法在测量精度上好于Gauss拟合方法，测量精度弥散程度较小。由于ePSF拟合方法是在Gauss拟合方法确定的初始条件的基础上的进一步处理，全部被测星的测量精度都有所提高，ePSF拟合方法与Gauss拟合方法的精度随星等的变化趋势基本一致。

在分析比较测量精度时，剔除了标记为39的星像。该星是本文所测星中最暗的星，在利用Gauss拟合求解初始参数时只有5个像素参与计算，使得结果存在较大误差，最终导致ePSF拟合偏差较大。用Gauss拟合测量精度为1.4 mag，而有效点扩散函数的方法的测量精度为1.8 mag。

图8 本文方法与Gauss拟合法内部测量精度比较Fig.8 Comparison of the internal accuracies of our method and the Gaussian fitting method

4 讨论和结论

本文对国家天文台1 m望远镜观测的16幅CCD图像进行实际测量。结果表明:采用有效点扩散函数拟合方法在测量精度上好于Gauss拟合方法。本文方法平均测量精度达到0.015 mag，最好测量精度可达0.001 5 mag;而利用Gauss拟合平均精度只有0.05 mag，最好的精度为0.013 6 mag，本文方法平均精度提高了3倍。从图8中可看出暗星的测量精度不如亮星的。通过计算可得到精度偏差是0.005，而Gauss拟合精度偏差是0.01，可见本文采用的方法拟合结果比较稳定，是一种更优的测光方法。通常光学系统的点扩散函数符合Gauss分布，但由于大气等因素的影响，致使星像分布并不完全符合Gauss分布，本文通过数值的方法列出点扩散函数在对应采样点的值，并不需要用函数表达式去拟合星像，因而比较符合实际的星像灰度分布。在计算速度上，本文的方法比Gauss拟合的方法较慢，主要是ePSF的求解过程所需运算量较大，但在天文观测的后续处理分析实时性要求不高时，本文的方法是可行。另外，本方法需要对星像中心位置、通量及背景进行初始估计，因而可通过Gauss拟合的方法得到这些初始条件，进而运用有效点扩散函数拟合方法提高测量精度。

致谢:感谢彭青玉教授为本文提出了重要和建设性建议及提供的图像资料。

［1］Mighell K J.Algorithms for CCD Stellar Photometry［J］.ASPC，1999，172:317 －328.

［2］Mighell K J.CCD Aperture Photometry［J］.ASPC，1999，189:50 －55.

［3］Handler G.Combining Aperture and PSF-Fitting Photometry［J］.BaltA，2003，12:243 －246.

［4］洪禅伟，周曙白，陈洛恩.Blazar短时标光变的孔径测光分析［J］.天文研究与技术——国家天文台台刊，2008，5(4):330－336.Hong Shanwei，Zhou Shubai，Chen luoen.Analysis of the Aperture Photometry for Biazar［J］.Astronomical Research ＆ Technologh——Publication of National Astronomical Observatories of China，2008，5(4):330 －336.

［5］Stetson P B.DAOPHOT-A Computer Program for Crowded-field Stellar Photometry［J］.PASP，1987，99(613)，191－222.

［6］Mighell K J.The MATPHOT Algorithm for Digital Point Spread Function CCD stella rphotometry［J］.ASP Conference Series281:Astronomical Data Analysis Software and Systems XI，2002:387－391.

［7］Anderson J，King I R.Toward High-precision Astrometry with WFPC2.I.Deriving an Accurate Point-spread Function［J］.PASP，2000，112(776)，1360 －1382.

［8］Anderson J，Bedin L R，Piotto G，et al.Ground-based CCD Astrometry with Wide Field Imagers.I.Observations just a few Years Apart Allow Decontamination of Field Objects from Members in Two Globular Clusters［J］.A＆A，2006，454(3):1029 －1045.

［9］Da Costa GS.Basic Photometry Techniques［J］.ASPC，1992，23:90 －104.

［10］王娴，苏成悦，王婷婷，等.一种新的星像自动搜索算法［J］.广东工业大学学报2009，26(3):77－81.Wang Xian，Su Chengyue，Wang Tingting，et al.A New Plexible Stellar Auto-Searching Algorithm［J］.Journal of GuangDong University of Technology，2009，26(3):77 －81.

［11］李展，彭青玉，韩国强.CCD图像数字定心算法的比较［J］.天文学报，2009，50(3):340－348.Li Zhan，Peng Qingyu，Han Guoqiang.Comparison of Digital Centering Algorithms Based on CCD Images［J］.AAS，2009，50(3):340 －348.

［12］张志渊，彭青玉.ePSF拟合法与Gaussian拟合法的比较，天文研究与技术——国家天文台台刊，2010，7(2):132－139.Zhang Zhiyuan，Peng Qingyu.Comparison of Fitting EPSF and Fitting Gaussian-Functions［J］. Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2010，7(2):132 －139.