多相滤波器组谱分析方法的性能讨论与天文观测应用*

朱凯，甘恒谦，朱岩，金乘进

(中国科学院国家天文台，北京 100012)

对天体辐射信号的功率谱分析可以获得射电源辐射机制、运动性质等诸多信息。在射电天文数字终端设备中，对信号进行谱分析主要采用自相关或周期图方法［1］;另一方面，以多相结构实现的数字滤波器组能够实现信号的均匀子带分解，在数据流与计算量上相对于滤波器组的直接实现有很大的降低，因此应用多相滤波器组［2］进行谱分析，也是一种可选择的方案，如GALFA中性氢巡天项目所用的频谱仪即基于多相滤波器组进行研制。本文拟对这种方法的原理进行分析，并从仿真和实测上与通常的周期图方法性能进行比较，以得到有参考意义的结果。

本文内容组织如下，第1节简要介绍多相滤波器组的原理，第2节对PFB谱估计器的统计性能和计算量进行讨论，并与具有相同通道数及相同单位样值响应长度(即原型FIR滤波器长度)的周期图方法分别进行比较，第3、4节介绍仿真与实测的结果。

1 PFB原理简述

多相滤波器组是数字滤波器组的一种高效实现形式［3］，用于对信号进行均匀子带分解。所谓均匀子带分解，是指滤波器组中的每一个子带滤波器具有相同的通带宽度，依次占据信号整个频带，从而将信号分解为若干个相同带宽的子带信号，其频谱分解过程如图1。

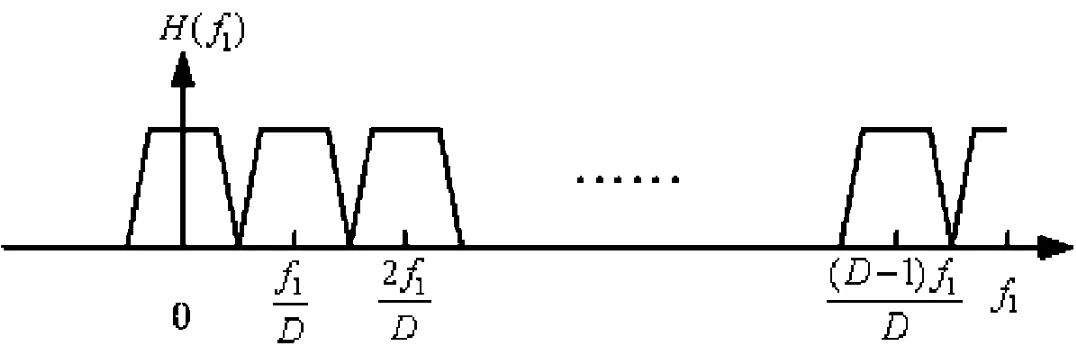
图1 信号的均匀子带分解示意Fig.1 Uniform sub band decomposition of a signal

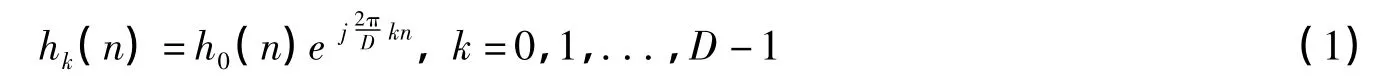
其中h0(n)为低通滤波器的单位样值响应，hk(n)为第k个子带滤波器的单位样值响应，由于各子带滤波器均通过低通滤波器得到，因而此低通滤波器也被称为原型低通滤波器。

通常，对每一个子带信号，经带通滤波之后都需要进行混频、抽取处理。可以证明，对均匀划分的多通道滤波器组，上述子带处理过程可以用图2中更为高效的多相结构形式实现［4］，也即多相滤波器组。

上图所示的均匀子带分解过程中，低通滤波器通带为［－f1/2D，f1/2D］，第k个子带滤波器的通带为［(2k－1)f1/2D，(2k+1)f1/2D］，并且上述数字滤波器均为有限冲激响应(FIR)滤波器。由于滤波器组的通带划分具有均匀性，因此各子带滤波器的频率响应可以由其中的低通滤波器经频谱搬移得到，此频谱搬移过程可表示为:

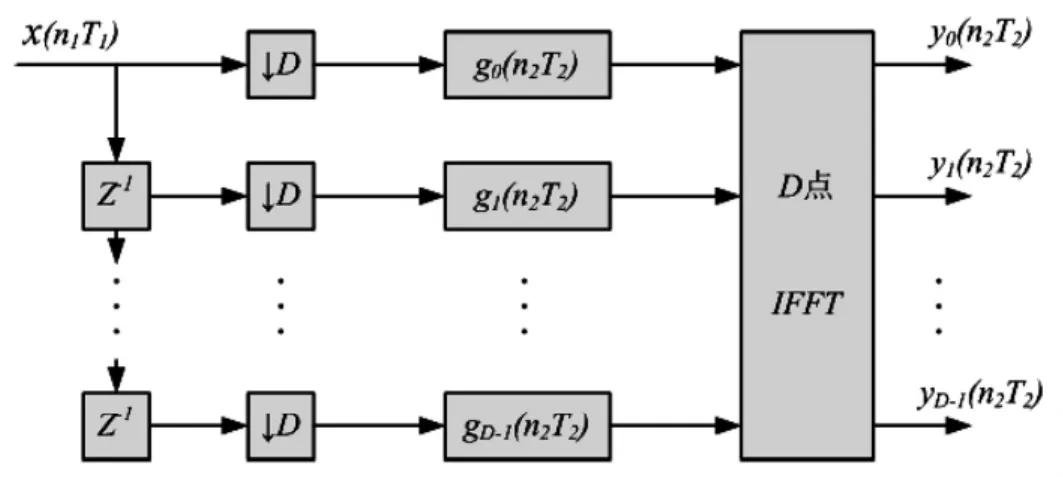
图2 多相滤波器组结构Fig.2 Structure of the polyphase filter bank

图中抽样时间T2=DT1，第ρ个子带的滤波器单位样值响应为:

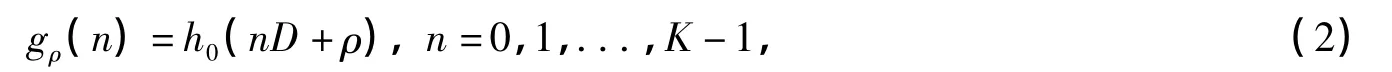
第ρ个子带输入的信号变为x(nD－ρ)，是对原信号进行ρ点延迟和D倍抽取后的结果。

相对于直接实现的滤波、混频、抽取处理，多相滤波器组将信号的抽取提前，同时对滤波器单位样值响应也进行了抽取和重排列，子带滤波器的单位样值响应长度从KD下降为K，从而大大降低了资源量。

2 谱估计性能

随机信号x(n)的功率谱定义为:

其中，r(k)是输入信号x(n)的自相关函数，理论上信号的自相关函数需要通过无限长信号的计算得到，但是由于实际采集到的信号样本长度总是有限的，因此需要利用有限样本估计无限长信号的功率谱，即构成一个信号参数估计问题。

实际中应用最普遍的谱估计算法是基于FFT的周期图方法，周期图方法在大样本量场合下是一个良好的谱估计器，将多相滤波器组用于功率谱估计，也构成一个谱估计器，下面对其性能进行讨论，并与周期图方法进行比较。

下面的讨论中，如无特别说明，均设定多相滤波器组通道数为D，多相结构下的子滤波器长度(又称多相因子)为K，对应的原型滤波器长度为N=KD。

对于谱估计方法性能的讨论总是在有限样本长度的条件下进行的，需要区分大样本量与小样本量情况。对于PFB方法，显然在小样本量(如L＜KD)的情况下是不适用的。此处仅考虑样本数L大于原型滤波器长度N=KD的情况，设样本数为N的整数倍，L=MN。输入信号记为:

2.1 PFB谱估计原理

应用滤波器组进行信号功率谱估计的原理如图3。

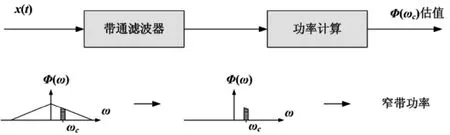
图3 应用滤波器组进行功率谱估计Fig.3 Estimation of power spectrum with filter banks

图中上部为信号处理的流程，下部为信号频谱的变化。通过对带通滤波后的信号进行功率计算，功率计算是一个积分平均的过程，由此得到该通带内信号功率的估计值。设计一组带通滤波器，使其通带之和覆盖整个信号带宽，就可以估计出输入信号的功率谱。

对信号进行带通滤波和功率计算，实际上是对信号功率谱进行了平滑。而对于不同的带通滤波器形式、以及不同的滤波器组实现方案，会具有不同的估计性能。

D通道PFB谱估计器首先将所有样本数据有重叠的分成MK个子段，每一子段含KD个样本数据，每一子段相对于上一子段新增D个样本，分段方法如图4。

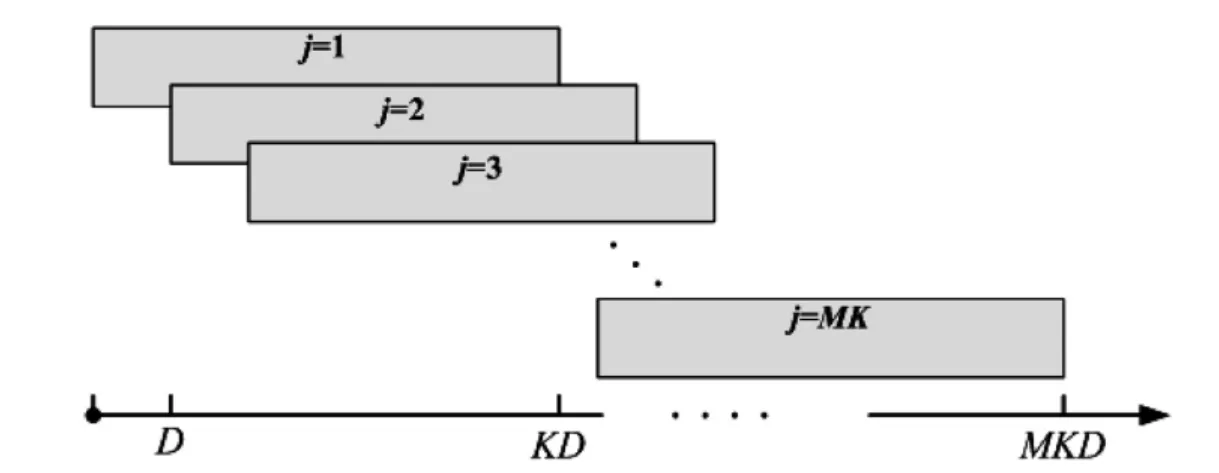
图4 D通道PFB谱估计器的样本分段方式Fig.4 The segmentation of the D-channel PFB estimator

然后对上述的每一子段样本依次进行D通道的子带滤波，由PFB处理过程与图2的等效性可知，PFB是采用单位样值响应长度为KD的原型滤波器进行子带滤波，因此对于每个子段KD个样本输入，每个频率通道仅得到一个稳定的滤波输出，在频率ωk位置，第j子段的输出值可表示为:

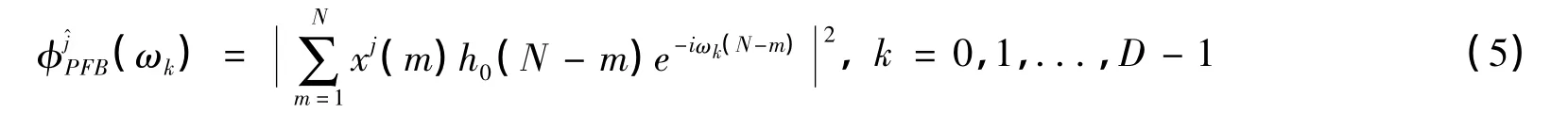
其中xj(m)=x［(j－1)N+m］，为第j子段的第m个样本;h0(n)为原型低通滤波器的单位样值响应。利用所有子段共MK个稳定输出值进行功率计算，频率ωk处功率计算的结果为所有子段输出值的均值，可表示为:

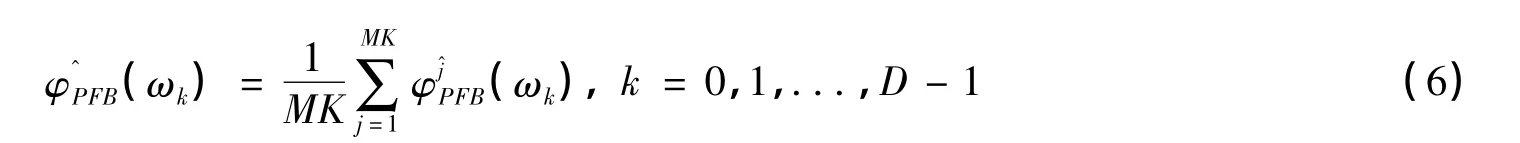
在滤波器组通道数D确定的情况下，对信号功率谱的估计总是有偏差的。在样本数趋于无限时，频率ωk处功率谱的估计结果收敛到此通道处带通滤波器的频率响应与输入信号真实功率谱乘积的积分，从而估计偏差也可由此得到。

对于PFB滤波器组，所有子带滤波器的频率响应都取决于原型低通滤波器的设计，而通常通过选择合适的多相因子K和滤波器设计方法，可以获得很好的滤波器频响特性，因此相对于同通道数的周期图方法其估计偏差更低，下面对此进行比较。

2.2 偏差比较

作为比较对象，考虑常见的周期图(即FFT)谱估计方法，在相同的样本量L=MN的条件下，分相同通道数和相同样值响应长度两种情况，与PFB谱估计法进行比较。

(1)相同通道数D

D通道Bartlett周期图方法将数据无重叠的分成MK个子段，每个子段含D个样本，首先计算FFT得到每个子段上的功率谱观测值，然后，利用所有子段共MK个观测值进行功率计算。可将周期图等效为滤波器组，则对应的周期图滤波器组第k通道滤波器的单位样值响应为:

此滤波器的样值响应长度为D，通带宽度为1/D，对应的传递函数为:

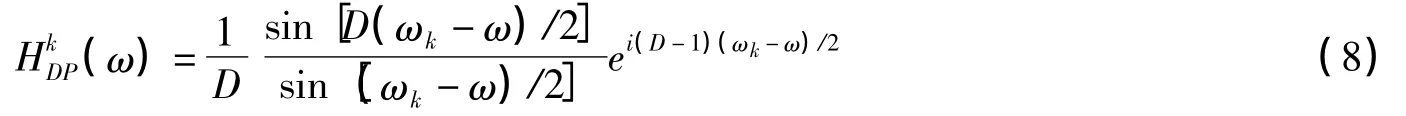
例如对于D=128，周期图低通滤波器的频响曲线如图5中的细实线所示，图中横坐标为归一化圆频率，抽样频率归一化为2π，纵坐标为滤波器幅频响应。图中粗实线同时也给出了D=128，多相因子K=8，采用Parks-McClellan等纹波方法设计的PFB低通滤波器的幅频响应，点划线为通道数D的理想通带形状。D通道PFB与周期图滤波器性能参数如表1。

图5 相同通道数的周期图与PFB滤波器频率响应(D=128;K=8)Fig.5 Frequency responses of the D-channel periodogram and PFB filters(—both have D=128;K=8)

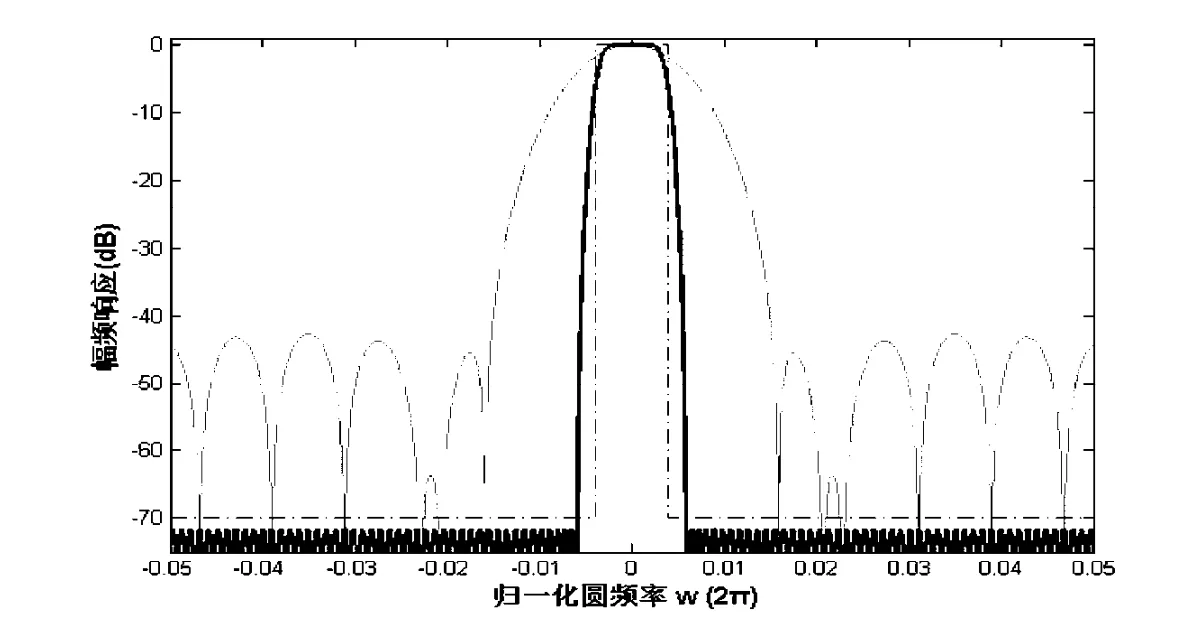
图6 相同通道数的加Hamming时间窗周期图与PFB滤波器频率响应(D=128;K=8)Fig.6 Frequency responses of the D-channel periodogram and PFB filters with Hammming time windows(—both have D=128;K=8)

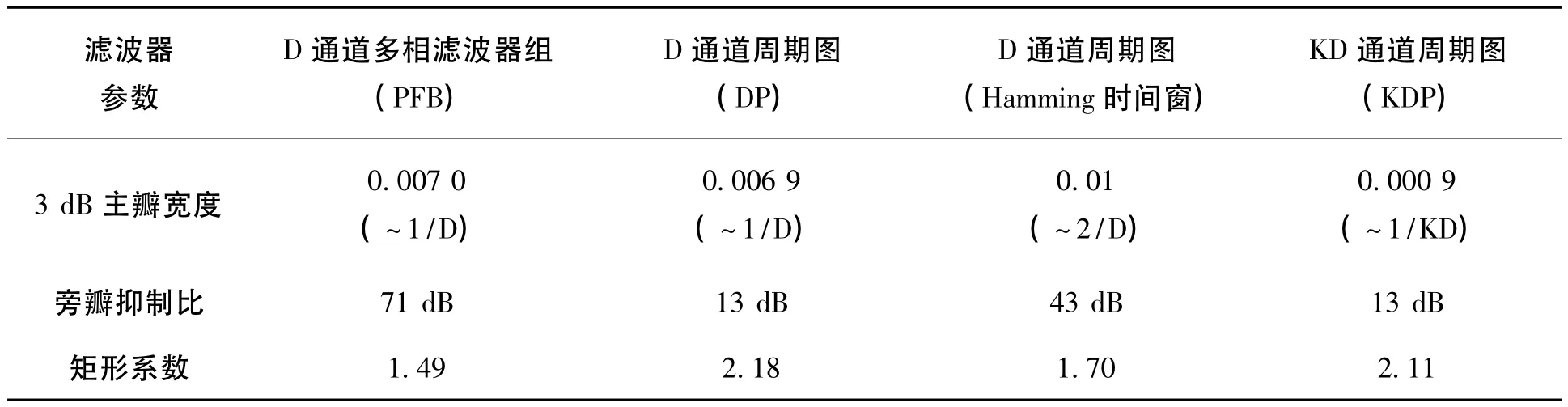
表1 PFB与周期图滤波器参数比较Table 1 Comprison between PFB and periodogram filters

表中矩形系数定义为30 dB带宽与3 dB带宽比值，同时列出的包括KD通道周期图的滤波器性能参数。

在相同的谱分辨率即通道数D条件下，谱估计器的性能取决于滤波器的通带特性(通带矩形系数与旁瓣抑制水平)，由此来看，PFB方法能够获得比周期图滤波器更好的通带矩形系数和旁瓣抑制性能，因而从理论上来说应该能够获得更好的谱估计质量。

图6和表1中给出了加Hamming时间窗(直接加在样本数据而非自相关函数上)的周期图与同通道数PFB的比较结果。加窗周期图在提高旁瓣抑制比性能的同时，降低了通带选择性能。可以看到，在加Hamming时间窗的情况下，对应的旁瓣抑制比提高到43 dB，但滤波器主瓣宽度增加了约1倍。周期图方法的旁瓣抑制比和主瓣宽度是一对矛盾，在保持谱通道数不变的情况下，加窗可以改善旁瓣抑制水平，但要以损失一定的主瓣选择性能为代价。而PFB可以较好地解决这个矛盾，在相同谱通道数情况下，在增加旁瓣抑制比的同时，仍然保持原有的主瓣3 dB带宽，并且具有更好的通带矩形系数。

不过，与周期图方法相比，PFB在提高通带性能的同时，也付出了额外的代价，因为在相同通道数的限制下，PFB使用了具有更长单位样值响应的滤波器;而一般来说，单位样值响应更长的滤波器总是对应着更多的计算量和资源，因此下面对相同单位样值响应长度条件下的PFB与周期图方法性能进行比较。

(2)相同单位样值响应长度KD

由(8)式知，周期图滤波器的单位样值响应长度与其谱通道数总是相等的，因此在滤波器样值响应长度KD的条件下，周期图方法可达到的通道数为KD，这是PFB方法的K倍。对于KD通道周期滤波器，其性能与D通道周期图相似，只需将参数D换成KD即可。

对应D=128、K=8，具有相同单位样值响应长度KD=1024的PFB与周期图滤波器频率响应如图7，而对应滤波器性能参数列于表1中。

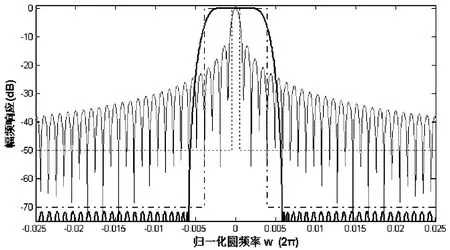
图7 相同单位样值响应长度KD=1024的周期图与PFB滤波器频率响应(D=128;K=8)Fig.7 Frequency responses of periodogram and PFB filters with the same unit of sampling response time(—both have D=128;K=8)

其中粗实线为128通道的PFB原型滤波器的幅频响应，细实线为相同单位样值响应长度周期图滤波器的幅频响应，点划线和点线分别128通道和1024通道的矩形通带示意。KD通道周期图的滤波器性能参数见表1。

从图7和表1可见，在相同的单位样值响应长度内，周期图方法可以取得此情况下能达到的最高谱分辨率，PFB方法则是通过放松对分辨率的要求，以换取更好的通带矩形系数和旁瓣抑制性能，在这一点上PFB与加窗的效果是相似的。

2.3 估计方差

在样本量足够大的情况下，上述几种方法的估计方差可以降低到足够小，但是方差下降速度有所不同。PFB与D通道周期图都是在每D个滤波输出中抽取了一个输出用于功率计算，而KD通道周期图方法则是在KD个输出中抽取一个输出用于功率计算，因此对应于相同的样本量，KD通道周期图方差约为PFB和D通道周期图方法的K倍。或者说，PFB方法的方差降速是相同单位样值响应长度周期图方法的K倍。

从上面的分析可以看出，PFB的估计质量与直接实现的滤波器组是一样的，它相对于直接实现结构的优点在于计算量和存储资源上的大幅降低。下面对PFB方法实现所需的计算量、存储资源进行考察。

2.4 计算量与资源

下表列出了在KD个样本数据输入的情况下，上述3种方法的计算量、存储资源以及主瓣通道宽度、方差降低的水平。根据FFT实现方法不同，FFT暂存可能需要不同的存储量，此处以全并行方式计算。

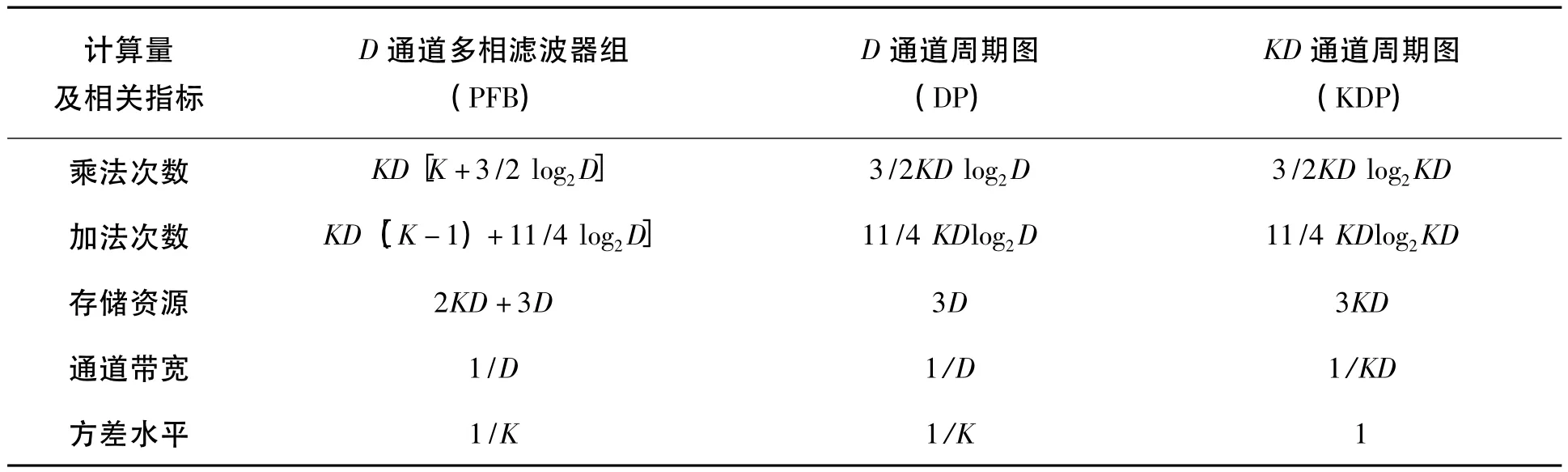
表2 PFB与周期图的计算量、资源需求、方差水平Table2 Calculation amounts，resource requirements，and variance levels of the PFB and periokogram filters

从上表中可以看到，在KD点样本输入的情况下，KD通道的周期图方法有更高的谱分辨率，而D通道的PFB与周期图方法的方差降低到其1/K的水平，有更快的方差下降降速，这意味实用中达到相同的信噪比需要更低的采集时间。依据上述表达式绘出3种方法计算量的曲线，如图8。

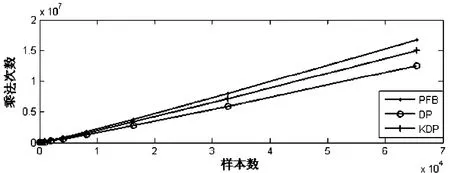
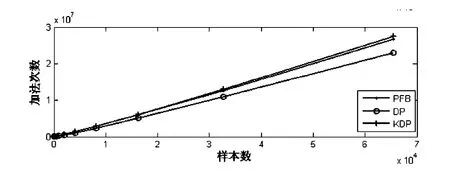
图8 3种谱估计方法计算量的比较Fig.8 Computation amounts of three estimation methods

可以看到，对于相同的输入样本量，3种方法中，D通道周期图的乘法与加法计算量均为最小，PFB的乘法量稍大一些。例如在16 384通道的情况下，PFB乘法次数为D通道周期图的1.38倍，为KD通道周期图计算量的1.14倍，几种方法的计算量大体在同一数量级上。

2.5 小结

从上述分析中得到的几个结论如下:

(1)与同通道数的周期图谱分析相比，PFB能够得到更接近理想带通响应的幅频响应，从而降低估计偏差，理论上可以获得更好的谱估计质量，但实现时需要增加一定的资源和计算量;

(2)与同单位样值响应长度的周期图谱分析相比，PFB仍然具有幅频响应和旁瓣抑制性能的优势，但谱分辨率较低，降低的倍数取决于多相因子K;

(3)与直接实现的滤波器组谱分析相比，PFB通过抽取大幅度降低了资源与计算量，这也是多相结构的主要优点之一。

需要说明的是，上面的结论都基于大数据样本谱分析的情形，对于小样本情况，无论是PFB还是周期图方法都需要在方差性能和分辨率之间进行折中，有时可采用参数化方法来提高分辨率［5］。

3 仿真

为检验PFB谱分析方法的效果，应用MATLAB进行仿真，构造一个4阶ARMA连续谱加单频正弦构成的输入信号，其中正弦信号的归一化频率为0.54π(采样频率为2π)，此信号的频谱如图9。

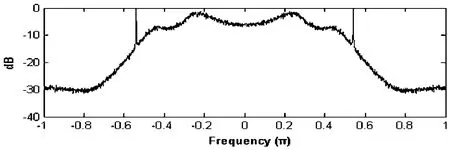
图9 输入信号的功率谱Fig.9 Power spectrum of the input signal

在仿真中模拟FAST密云模型接收机基带系统的处理过程(见下节)，对输入信号采用正交混频，将信号中心频率混至零频，进行双通道采集，获得原信号的IQ分量。由得到双通道IQ分量组成复信号只含有原信号的单边频谱。

分别应用K=8，D=2048通道PFB、2048通道周期图以及16 384通道周期图方法对此单边谱复信号进行谱估计，得到的功率谱如图10。

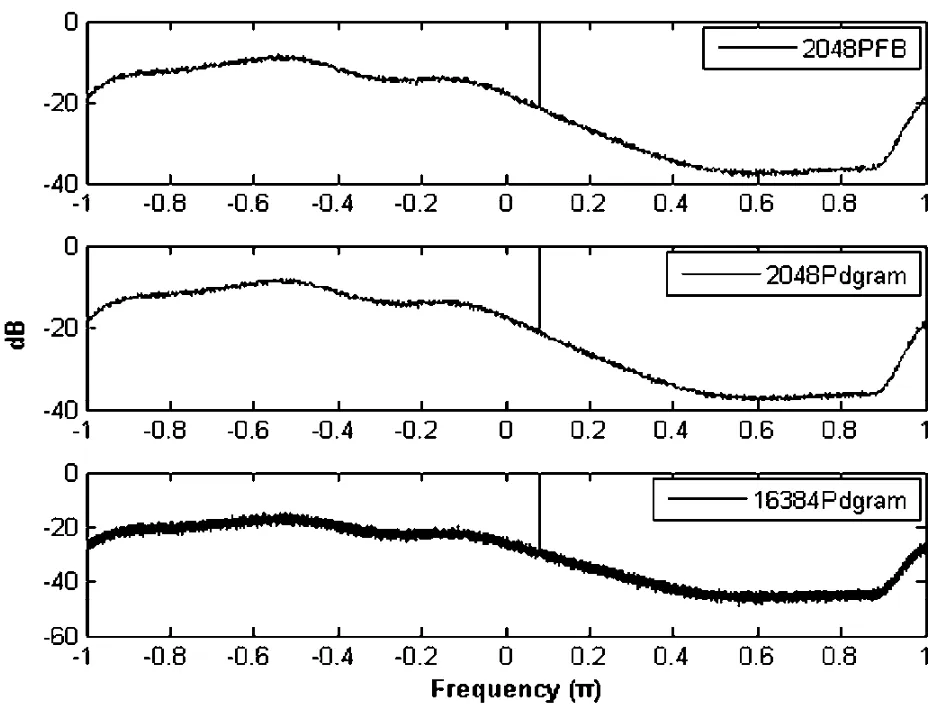
图10 PFB与周期图方法得到的功率谱Fig.10 Estimated power spectra with the PFB and periodogram filters

图10从上至下依次为2048通道PFB、2048通道周期图、16 384通道周期图方法得到的功率谱。在等量数据样本输入的情况下，2048通道数的PFB与周期图方法得到的功率谱估计结果没有大的差别，与相同单位样值响应长度(16 384通道)的周期图方法相比，方差更小。

在比较仿真结果中谱线强度与连续谱基线的差值上，下图要比上两图高8 dB，这说明16 384通道的周期图方法由于具有更高的分辨率，对于噪声中微弱的单频谱线的检测而言是有好处的。因此，在相同的资源消耗下，PFB有更好的频率选择特性，而周期图能够获得更高的谱分辨率，从这个意义上说，两种方法各有所长，实际中可以根据天文观测的科学目标进行选用。例如需要研究谱线的精细结构或谱线的漂移时，即可选用可获得更高分辨率的周期图方法。

4 实测

FAST接收机组利用FAST密云模型L波段接收机以及新研制的基带处理和数据采集系统进行了银河系中性氢谱线的观测实验，下面对此进行介绍。

FAST密云模型L波段接收机为单偏振接收机，中频带宽100 MHz，基带系统采用正交混频，如图11，模拟基带低通滤波器LPF带宽为5 MHz，之后进行双通道复采样信号，采样频率为10 MHz，得到有效带宽10 MHz的复信号。

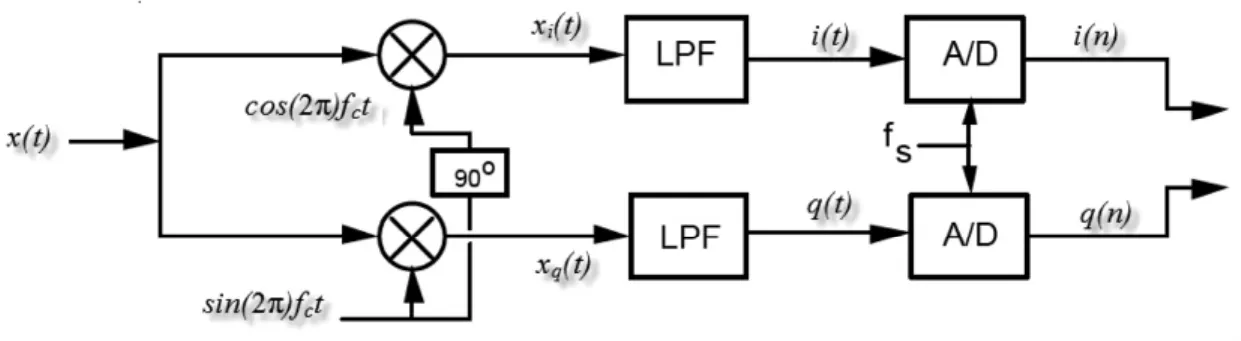
图11 FAST模型接收机基带系统信号处理流程Fig.11 Processing procedure of the baseband system of the MyFAST Receiver

基带处理系统实物如图12。

图12 FAST模型接收机基带系统实物Fig.12 Baseband system of the MyFAST Receiver

利用上述基带处理与数据采集系统采集得到的中性氢数据，取出nKD=8000×8×2048个样本，分别用2048通道PFB和周期图方法对采样数据进行处理。图13给出了样本信号分析得到的相对功率谱密度图，其中上部为PFB得到的功率谱，下部为2048通道周期图的结果。

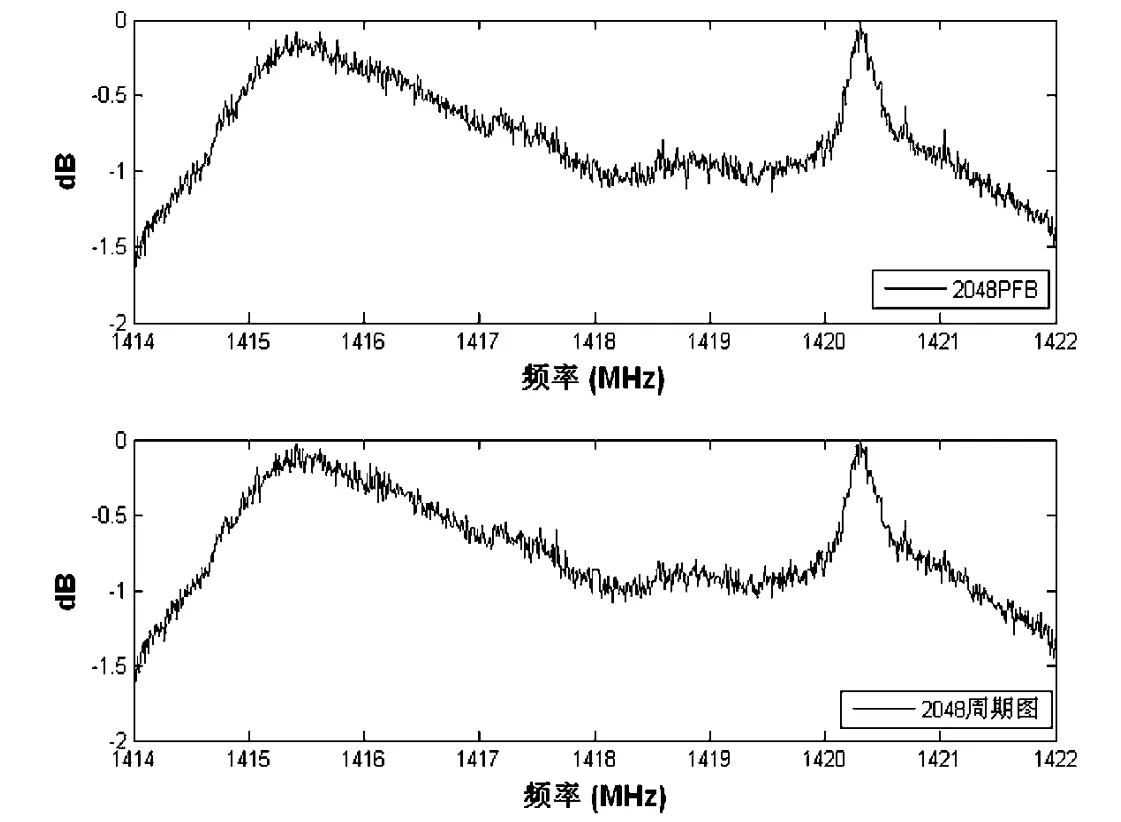
图13 PFB与周期图得到的HI信号功率谱Fig.13 HI line profiles observed with the PFB(upper)and Periodogram(lower)filters

从图中可见，HI谱线峰值位于频率1 420.3 MHz处。在相同样本数输入的情况下，两种方法得到的功率谱结果方差均为0.1 dB，可见两者的方差性能是相同的。而在图中所显示的频率范围内，上述两种方法得到的功率谱估计值之间的差值序列(PFB－FFT)如图14。

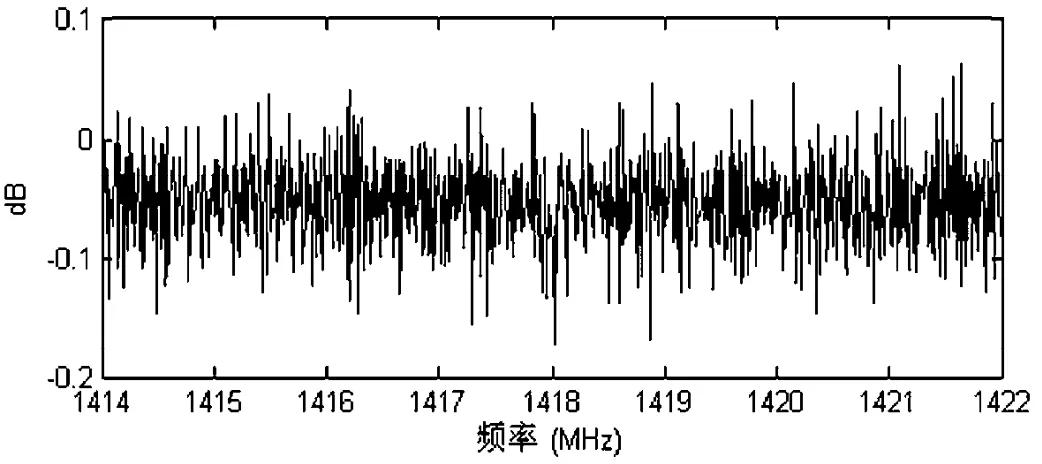
图14 PFB与周期图方法估计结果的差值Fig.14 Difference between the power spectra obtained with the PFB and periodogram filters

在图中所示的频率范围内，此差值序列的均值为－0.05 dB，两种方法估计结果之间存在很小的系统差值，这个差值实际上显示了频谱泄漏的大小。也即，在相同的通道数情况下，由于频谱泄漏，周期图方法的估计结果中多数通道的估计值较PFB方法更大，估计出的功率谱相对于PFB更加平滑，因此两者差值序列的均值小于0，这验证了PFB相对于周期图方法，获得了估计偏差性能上的改善。

5 结论

本文对多相滤波器组应用于谱分析的性能进行了讨论，利用多相滤波器组进行谱估计，由于滤波器相对于同通道数的周期图具有更好的频率响应、更少的频谱泄漏，理论上能够获得更好的估计质量。

在银河系21 cm中性氢谱线实测中，PFB估计效果与同通道数的周期图方法相比，方差性能相同，并降低了功率谱估计结果的偏差。由于快速增长的数字芯片性能与集成度使得应用PFB所需的资源变得越来越容易获得，因而PFB是一种很好的数字式频谱仪可选方案。另一方面，多相滤波器组作为一种信号子带分解和多抽样率处理的方法，在信号处理中的应用并不限于功率谱分析，如脉冲星消色散、VLBI基带转换［6］等场合也有很好的应用。

［1］胡广书.数字信号处理——理论、算法与实现［M］.北京:清华大学出版社，2005:496－526.

［2］Ronald E Crochiere，Lawrence R Rabiner.Multirate Digital Signal Processing［M］.Prentice-Hall，Inc，1983:290 －325.

［3］Fredric J Harris，Chris Dick，Michael Rice.Digital Receivers and Transmitters Using Polyphase Filter Banks for Wireless Communications［J］.Microwave Theory and Techniques，2003，51(4):1395－1412.

［4］董晖，姜秋喜，毕大平.多相滤波宽带信道化数字接收机［J］.雷达科学与技术.2007，5(1):73－77.Dong Hui， Jiang Qiuxi， Bi Daping. Polyphase Filtering Wide-Band Channelized Digital Receiver［J］.Radar Science and Technology，2007，5(1):73 －77.

［5］Petre Stoica，Randolph Moses.现代信号谱分析［M］.吴仁彪，韩萍，冯青，译.北京:电子工业出版社，2007:69－87.

［6］陈岚，张秀忠.用于VLBI数字基带转换的多相滤波技术研究［J］.天文学进展，2008，26(1):87－94.Chen Lan，Zhang Xiuzhong.The Study of DBBC Based on Poly-phase Filter Banks and FFT in VLBI［J］.Progress in Astronomy，2008，26(1):87 －94.