三角形蜂窝在面内冲击荷载下的力学性能

胡玲玲，陈依骊

(中山大学 工学院应用力学与工程系，广州 510275)

三角形蜂窝在面内冲击荷载下的力学性能

胡玲玲，陈依骊

(中山大学 工学院应用力学与工程系，广州 510275)

通过数值计算研究规则排布和交错排布的三角形铝蜂窝在面内冲击荷载下的变形模式、承载能力以及能量吸收特性。结果表明两种蜂窝的变形均随着冲击速度的增加或胞壁厚度的减小而向冲击端集中，规则排布的蜂窝沿着局部变形带逐行压溃直至密实，而交错排布蜂窝的变形模式可分为4种。铝蜂窝吸收的能量绝大部分转化为变形所需的内能，动能所占比重较小。随着冲击速度的提高，两种排布方式的蜂窝均表现出更强的承载能力和能量吸收能力，但内能在总能量中的比重减小，动能比重增加。规则排布的蜂窝比交错排布的蜂窝具有更高的承载力和能量吸收能力，该差别主要是由于二者内能的不同所引起，且该差值在交错排布蜂窝“核区”形成后逐渐减小。

蜂窝;冲击;变形模式;能量吸收

蜂窝作为一种多胞材料，具有良好的能量吸收能力、较高的比强度和比刚度等优异性能，因此将其做成轻质结构和能量吸收构件，在航空航天、汽车工业、交通运输等领域有广阔的应用前景［1］。作为吸能材料其往往受到冲击荷载的作用，因此对其动态力学性能的研究已成为近年来的一个研究热点。Ruan［2］，Zou［3］等通过数值计算研究了六角形蜂窝的变形模式和承载能力。Hu 和 Yu［4，5］根据六角蜂窝在高速冲击下的变形模式提出理论模型，推导了其承载力和能量吸收能力的表达式，并对各种能量的分配进行了讨论。卢文浩等［6］运用理论分析和有限元数值计算对六角形蜂窝单个胞体和多个胞体在动态冲击下的变形情况和能量吸收能力进行了研究。Papka等［7，8］通过实验和数值计算研究了圆形胞元蜂窝的力学性能，Hu和Yu［9］通过定义非均匀指标讨论了圆形胞元蜂窝在面内荷载下的非均匀变形。Liu等［10－12］对具有不同拓扑结构胞元的蜂窝进行了数值模拟，比较了它们的能量吸收性能。Zheng等［13］数值研究了不规则的随机蜂窝在面内冲击荷载下的动态力学性能。这些研究表明胞元结构的不同会使蜂窝展现出不同的变形模式和动态力学性能。因此除了传统的六角形蜂窝外，我们需要深入了解具有其它胞元结构的蜂窝的力学行为，为蜂窝胞元结构的优化设计奠定基础。

本文通过数值计算研究规则排布和交错排布的三角形铝蜂窝在冲击荷载下的力学性能。对它们的变形模式进行分析和归类，比较两种蜂窝应力－应变曲线的特点和平台应力值，并进一步分析它们的能量吸收性能和能量分配特点。

1 计算模型

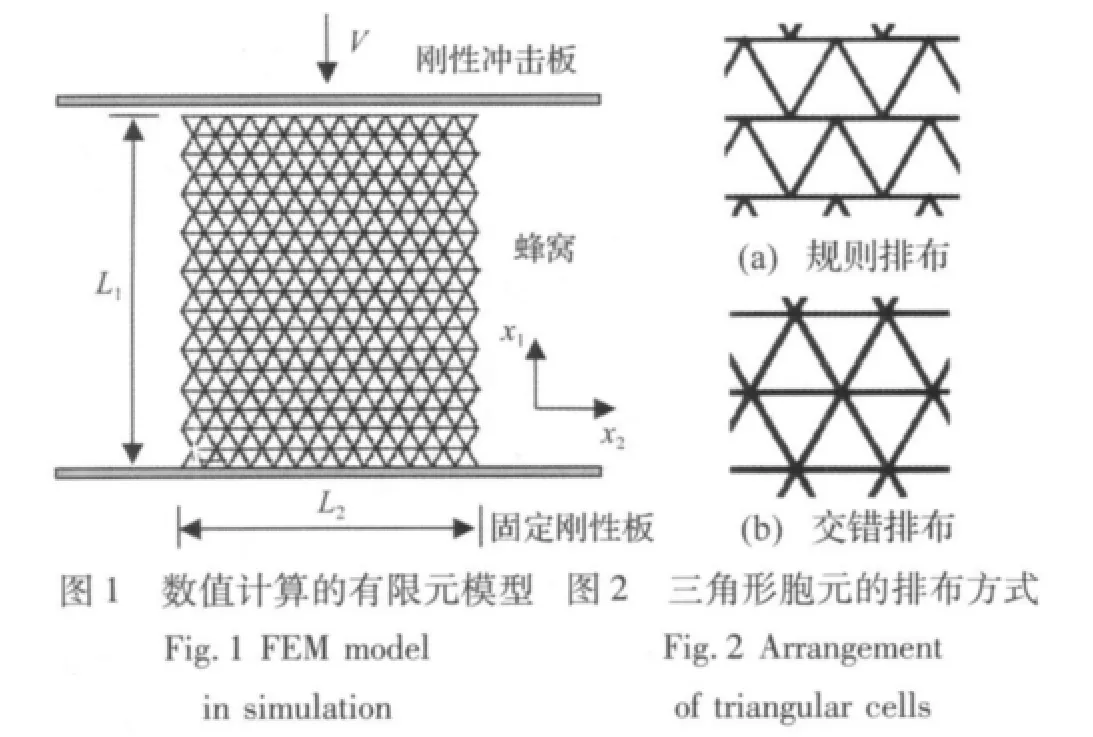
本文采用ANSYS－LSDYNA建立三角形铝蜂窝的有限元模型，如图1所示。该模型在x1和x2方向分别有18和25个胞，沿x1和x2方向的尺寸分别为L1=70.1 mm 和 L2=58.5 mm，模型的面外(沿 x3方向)厚度为b=0.5 mm。蜂窝的胞壁边长l=4.5 mm，壁厚h有5 种:0.1 mm，0.3 mm，0.5 mm，0.6 mm 和 0.8 mm。将铝蜂窝放置在一个固定的刚性板上，在其上方受到另一刚性板以恒定速度V沿x1方向的冲击。三角形胞元的排布分为规则排布和交错排布2种方式，如图2所示。计算中采用了不同的加载速度V，分别为10 m/s、35 m/s、70 m/s，110 m/s 和 140 m/s。胞壁采用理想弹塑性材料，杨氏模量 E=69 GPa，屈服应力σys=76 MPa，密度 ρs=2 700 kg/m3，泊松比 υ =0.3。刚性板的杨氏模量为210 GPa，密度为7 800 kg/m3。每个胞壁划分为16个壳单元，并限制各节点的面外位移以防止试件发生面外屈曲。对蜂窝设置单面自接触，蜂窝与上下钢板间设置面－面接触。

2 结果分析

2.1 变形模式

规则排布的蜂窝在所研究的速度范围和壁厚范围内变形模式差别不大:在冲击端首先形成第一局部变形带，位于底端的第二局部变形带稍后形成，随后胞元沿着第一、第二变形带交替变形，逐行压溃直至压实，如图3(a)所示。它们的主要区别在于加载速度越高，壁厚越薄，其变形越集中在冲击端，也即在形成第二变形带前有更多行的胞元在第一变形区被压溃，甚至不形成第2变形带，如图3(b)所示。

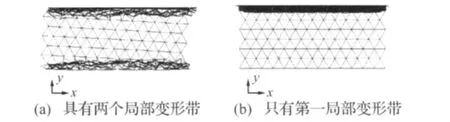
图3 规则排布三角形蜂窝的变形模式Fig.3 Deformation pattens of honeycombs filled with regular-arranged triangular cells

交错排布的三角形铝蜂窝在中低速冲击荷载下除了沿x1方向的压缩密实外，沿x2方向表现出横向收缩的特性，即“颈缩”现象，在冲击过程中逐渐形成内部“核区”，“核区”靠近固定端时称之为“下X模式”图4(a)，靠近冲击端时，称为“上X模式”图4(b)。这种“颈缩”现象导致了交错排布蜂窝在中低速冲击下特有的力学性能，如下文所讨论。在高速冲击下，蜂窝不会发生颈缩现象，而是形成靠近冲击端的局部变形带，胞体自上而下逐层压溃，直至底端，如图4(d)所示，称为“I模式”。“混合模式”图4(c)是“I模式”和“X模式”的过渡模式，既有轻度的颈缩现象，又形成局部变形带。

图4 交错排布三角形蜂窝的变形模式Fig.4 Deformation pattens of honeycombs filled with stagger-arranged triangular cells

交错排布三角形铝蜂窝在不同条件下的变形模式分类如图5所示。可见，冲击速度对蜂窝的变形模式影响很大，随着冲击速度的增加，蜂窝的变形模式由“下X模式”逐渐过渡到“上X模式”、“混合模式”，在高速冲击时形成“Ⅰ模式”。这反映了随着冲击速度的增加蜂窝的集中变形区域由固定端逐步向冲击端发展。减小胞壁厚度与提高冲击速度有着类似的效果。“X模式”和“混合模式”也说明交错排布的蜂窝比规则排布蜂窝更趋于整体变形。

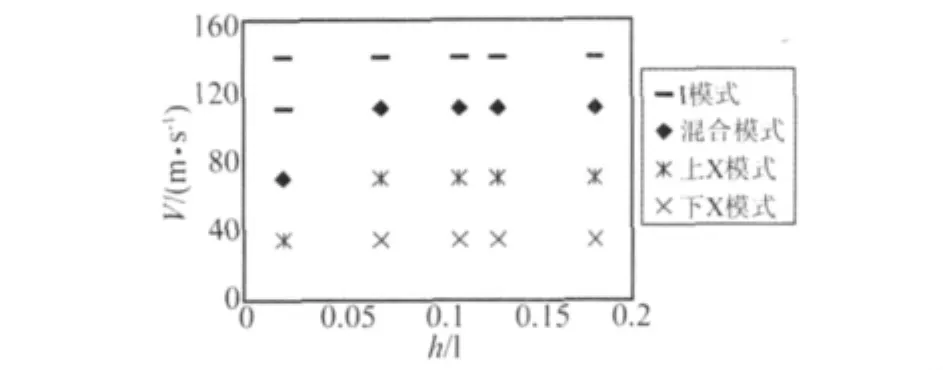
图5 交错排布三角形蜂窝的变形模式分类图Fig.5 Classfied chart of deformation pattens of honeycombs filled with stagger－arranged triangular cells

2.2 应力－应变曲线及平台应力

两种排布的铝蜂窝在中低速(35 m/s)和高速(110 m/s)冲击下的应力－应变曲线分别如图6(a)和图6(b)所示，其中R表示规则排布，S表示交错排布，下同。图中应力σ和应变ε分别定义为:

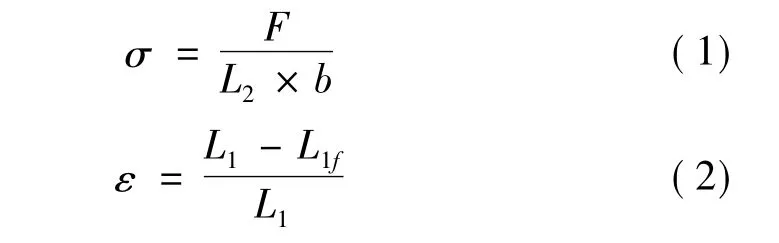
其中，F为刚性冲击板与蜂窝试件间的接触力，L1f为试件变形后沿x1方向的尺寸。

由于交错排布的三角形蜂窝更趋于整体变形，其动力响应相对稳定，应力－应变曲线的振幅较小。规则排布的蜂窝和高速冲击下的交错排布蜂窝都具有比较稳定的应力平台区，但当冲击速度较低时图6(a)，交错排布蜂窝的应力平台区在经历一个平稳阶段后(图中应变大于0.2后)开始明显上升，这种现象存在于所有发生“X变形模式”的工况中。究其原因，“X模式”特有的颈缩现象使试件在纵向对称轴附近表现出较高的局部刚度区，随着压缩量的增大，“核区”逐渐形成，从而提高了蜂窝的承载能力。并且加载速度越大，“核区”形成所对应的应变也越大。

将应力－应变曲线平台阶段的应力取平均作为铝蜂窝的平台应力值，图7给出了两种排布方式的蜂窝分别在35 m/s和110 m/s的冲击速度下平台应力值随胞壁厚度的变化曲线。由图可见，两种排布方式蜂窝的平台应力值均随着胞壁厚度的增加而增加，冲击速度越高，它们的平台应力也越大。规则排布的蜂窝比交错排布的蜂窝具有更高的承载能力，并且加载速度越大，二者之间的差别也越明显。

2.3 能量吸收性能

2.3.1 比能量

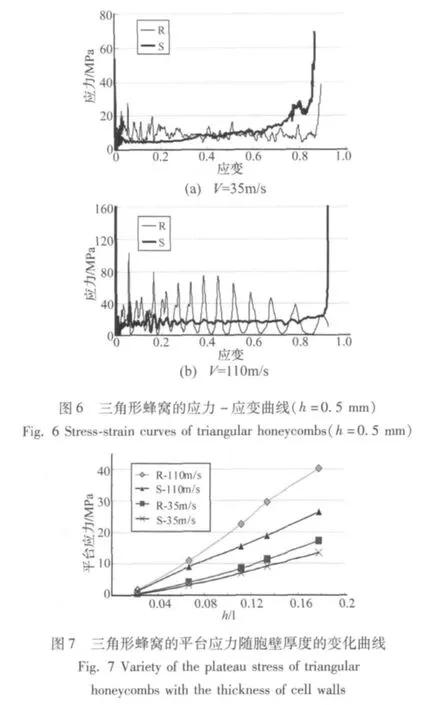
图8为胞元壁厚为0.5 mm的三角形铝蜂窝在不同加载速度下的比能量－应变曲线，其中比能量指单位体积吸收的能量，等于应力对应变的积分。结果表明，随着冲击速度的提高，两种排布方式的蜂窝均表现出更强的能量吸收能力。当冲击速度为高速时，规则排布蜂窝的能量吸收能力明显强于交错排布的蜂窝材料。而对于中低速冲击的情况，在应变不大时，规则排布蜂窝的能量吸收能力强于交错排布的蜂窝材料;随应变的增加，规则排布的三角形蜂窝的吸能曲线渐趋平缓，而交错排布的曲线的斜率逐渐增大，使其在达到一定应变后甚至超过规则排布蜂窝的曲线。这与交错排布蜂窝在中低速冲击下内部形成的“核区”有关，“核区”的形成提高了蜂窝的承载能力，从而使其能量较快地增加。又由于较高的冲击速度下，“核区”形成于较大的应变，因此两种蜂窝的曲线的交点所对应的应变值随冲击速度的增加而增加。

2.3.2 能量分配

在整个冲击过程中，蜂窝所吸收的能量主要转化为两大部分，即蜂窝的内能和动能，此外还有一小部分能量通过摩擦、热能等形式耗散掉。本文重点讨论内能和动能这两部分能量，并将二者之和定义为总能。在有限元计算中，蜂窝的内能I和动能K的计算公式分别为:

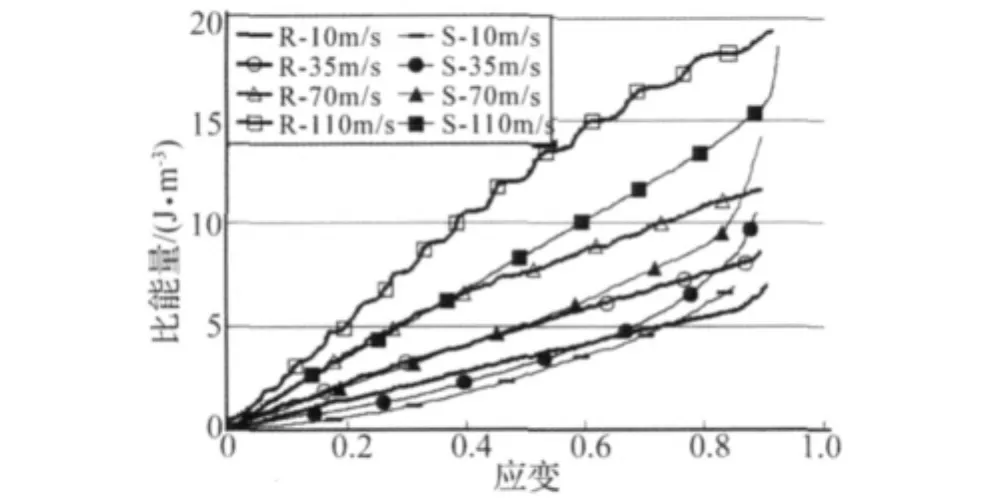
图8 三角形蜂窝在不同冲击速度下的比能量－应变曲线 (h=0.5 mm)Fig.8 Specific energy-strain curves of triagular honeycombs under various impact velocities

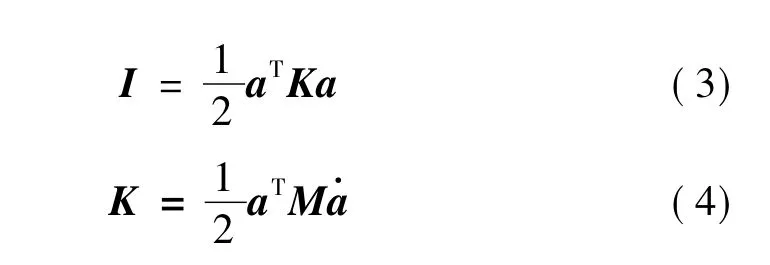
其中，a为单元节点位移向量，K为单元刚度矩阵，M为单元质量矩阵。

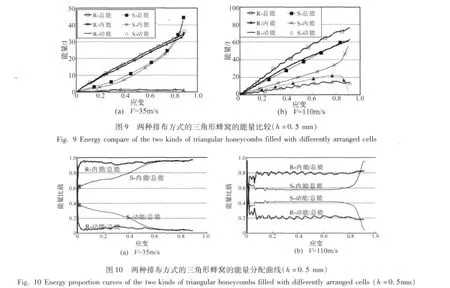
两种排布方式的三角形铝蜂窝的能量比较曲线如图9所示。交错排布蜂窝在变形过程中的动能比规则排布的大，两种排布方式吸能能力(总能)之间的差别主要来自于内能，并且该差值在交错排布蜂窝的“核区”形成后逐渐减小。

图10展示了两种方式排布下的蜂窝的能量分配曲线。规则排布蜂窝所吸收能量中内能与动能的比值相对稳定，且80%以上的能量转化为内能，其动能所占比重较交错排布的蜂窝小。在高速冲击下图10(b)，两种排布的蜂窝均以局部变形带的形式逐层压溃，因而它们的动能在受冲击的初始时刻随应变增加急速上升，占能量的主要部分，随着胞元发生塑性变形，胞元逐行压溃，内能随之增大，在进入平台区后稳定在某一值(规则排布在80%左右，交错排布在60%左右)。中低速时图10(a)，交错排布的蜂窝趋于整体变形，因而在变形过程中其内能比重逐渐增加，动能比重逐渐减小，最终达到并稳定于与规则排布蜂窝相当的水平。另外，图10也显示出冲击速度越大，两种蜂窝的动能所占比重也越大，内能比重越小。

3 结论

(1)冲击荷载下，规则排布的三角形蜂窝沿着局部变形带逐行压溃直至密实，而交错排布的蜂窝在不同条件下的变形模式差异很大，可归纳为“下X模式”、“上X模式”、“混合模式”和“I模式”4种变形模式;两种排布的蜂窝均表明加载速度越高，胞壁厚度越薄，其变形越向冲击端集中。

(2)蜂窝吸收的能量绝大部分转化为变形所需的内能。随着冲击速度的提高，两种排布方式的蜂窝均表现出更强的承载力和能量吸收能力，但内能在总能量中的比重减小，动能比重增加。

(3)规则排布的蜂窝比交错排布的蜂窝具有更高的承载力和能量吸收能力，并且加载速度越大，二者之间的差别也越明显。该差别主要是由于二者内能的不同所引起，并且该差值在交错排布蜂窝“核区”形成后逐渐减小。

［1］ Gibson L J，Ashby M F.Cellular Solids:Structure and Properties，2nd ed.Cambridge University Press，1997.

［2］Ruan D，Lu G，Wang B，et al.In-plane dynamic crushing if honeycombs finite element study.Int J Impact Eng，2003;28:161－182.

［3］ Zou Z，Reid S R，Tan P J，et al.Dynamic crushing of honeycombs and features of shock fronts.Int J Impact Eng，2009:36(1):165－176.

［4］ Hu L L，Yu T X.Dynamic crushing strength of hexagonal honeycombs.Int J Impact Eng，2010，37:467 －474.

［5］胡玲玲，余同希.惯性效应对蜂窝能量吸收性能的影响［J］.兵工学报，2009，30(52):24 －27.

［6］卢文浩，鲍荣浩.动态冲击下峰窝材料的力学行为［J］.振动与冲击，2005，24(1):49－52.

［7］ Papka S D，Kyriakides S.Biaxial crushing of honeycombs-Part I:Experiments［J］.Int J Solids Struct，1999;36(29):4367－4396.

［8］ Papka S D，Kyriakides S.Biaxial crushing of honeycombs-Part II:Analysis［J］.Int J Solids Struct，1999;36(29):4397－4423.

［9］ Hu L L，Yu T X，Gao Z Y，et al.The inhomogeneous deformation of polycarbonate circular honeycombs under inplane compression［J］. IntJMech Sci， 2008，50:1224－1236.

［10］ Liu Ying，Zhang Xin-Chun.The influence of cell microtopology on the in-plane dynamic crushing of honeycombs［J］.Int J Impact Eng 2009:36(1):98 －109.

［11］张新春，刘 颖，章梓茂.组合蜂窝材料面内冲击性能的研究［J］.工程力学，2009，26(6):220－225.

［12］刘 颖，张新春.胞元微拓扑结构对蜂窝材料面内冲击性能的影响［J］.爆炸与冲击，2008，28(6):494－502.

［13］ Zheng Z，Yu J，Li J.dynamic crushing of 2D cellular structures:a finite element study［J］.Int J Impact Eng 2005;32:650－664.

Mechanical properties of triangular honeycombs under in-plane impact loading

HU Ling-ling，CHEN Yi-li

(Department of Applied Mechanics＆ Engineering，School of Engineering，Zhongshan University，Guangzhou 510275，China)

The deformation patterns，the load-bearing capacity，and the energy absorption behavior of honeycombs filled with regular-arranged and stagger-arranged triangular cells under in-plane impact were studied by using numerical simulation.The results showed that the deformation bound of honeycombs is gradually concentrated to the impact place with increase in impact velocity or decrease in cell wall thickness;the honeycomb filled with regular-arranged cells is crushed row by row to densification，while four kinds of deformation pattern are summed up for the honeycomb filled with stagger-arranged cells;most of the energy absorbed by honeycombs is converted into strain energy，while kinetic energy has a less proportion;with increase in impact velocity，both of the two kinds of honeycomb reveals stronger ability to bear load and absorb energy，the proportion of strain energy decreases with increase in impact velocity，while the proportion of kinetic energy increases;the honeycombs filled with regular-arranged cells have better load-bearing capacity and energy absorption ability than the ones filled with stagger-arranged cells due to their different strain energy，and the difference gradually diminishes after the core region in the honeycomb filled with stagger-arranged cells appears.

honeycomb;impact;deformation pattern;energy absorption

O347

A

国家自然科学基金项目(10802100);高校基本科研业务费中山大学青年教师培育项目(3161263)

2010－01－14 修改稿收到日期:2010－03－29

胡玲玲 女，博士，副教授，1980年10月生