Lanczos-QR方法在大型非比例阻尼结构复模态计算中的应用

张 静，刘明辉，郑钢铁，2

(1.哈尔滨工业大学 航天学院，哈尔滨 150001;2.清华大学 宇航学院，北京 100084)

Lanczos-QR方法在大型非比例阻尼结构复模态计算中的应用

张 静1，刘明辉1，郑钢铁1，2

(1.哈尔滨工业大学 航天学院，哈尔滨 150001;2.清华大学 宇航学院，北京 100084)

根据大型非比例阻尼结构的动力学模型特点，发展了适用于大型复特征值问题求解的Lanczos－QR方法。针对大规模非对称实矩阵的标准特征值问题，此方法首先采用Lanczos迭代方法对矩阵进行降阶;然后采用带移位的双重步位移QR方法求解降阶后的实三对角矩阵的全部特征值和特征向量，最后经过相应的变换得到原矩阵的特征解。另外，提出了分块矩阵三角分解方法将广义特征值进行标准化，该方既提高了计算效率，又避免了范数误差。还对奇异问题的处理进行了讨论。最后在FORTRAN语言中进行了程序实现，完成初步软件化，并且通过算例对算法及其程序的精度和收敛速度进行了验证。

特征值问题;非比例阻尼;Lanczos算法;QR算法

对于大型结构，除了建立精确的有限元模型［1］外，动力学计算方法的精确性也是保证结构动力分析精度的关键。结构模态分析又是各种动力分析的基础，其计算结果直接影响结构动力分析的精度［2］。常用求解特征值的方法有很多种:子空间迭代法［3］、乘幂(逆幂)法、Lanczos方法［4－5］、QR 方法，迭代Ritz向量法、Jacobi方法等，然而，对于大型非比例阻尼系统，上述方法均存在局限性。本文讨论系数矩阵具有如下特点的大型非比例阻尼结构的特征值问题:大型、稀疏、非对称、正定或半正定。这类大规模非对称实矩阵的标准特征值问题，解为复特征值和复特征向量，且只需要求解前若干阶较低的特征值和模态向量。

针对以上要求以及各种算法的特点，本文对求解大型非比例阻尼结构复模态问题的Lanczos-QR迭代法进行了发展。此方法结合了Lanczos算法快速高效和QR方法稳定可靠的优点，首先采用Lanczos迭代方法对矩阵进行降阶;再采用带移位的双重步位移QR方法求解降阶后的特征问题。本文还提出使用分块三角分解方法得到标准特征值问题，该方法在广义二次特征问题的标准化过程中具有明显的优越性，不仅减小了矩阵求逆的规模，并且避免了由于矩阵元素差异大引起的范数误差。另外本文还对刚度矩阵奇异时出现的问题进行了讨论和完善，从而得到标准的计算流程，并设置了与通用有限元软件NASTRAN的接口。最后通过算例验证了本文中的算法及程序的可实现性，结果表明本算法具有较强的收敛性，且稳定、可靠。

1 非比例阻尼结构的特征值问题

含有非比例阻尼系统的动力学方程为:

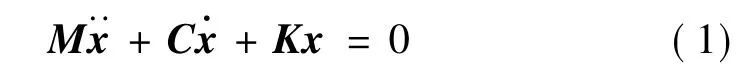
对于一般结构，矩阵M对称正定，矩阵K对称非负定。令y={x}T，将其化成等价的状态空间形式:

经过变换，得到广义特征值问题:

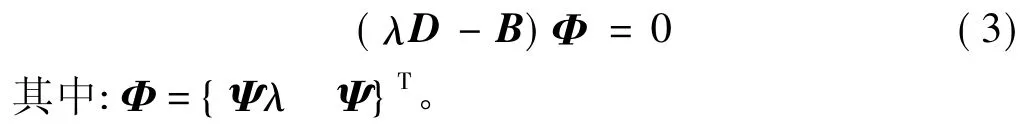
对于式(3)所示的非对称广义特征值问题，若矩阵B非奇异，则可化为如下的标准特征值问题的形式:

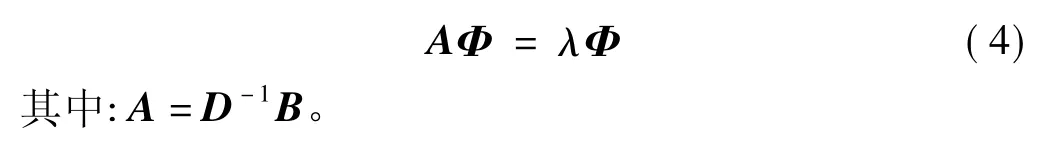
2 非对称矩阵特征问题的Lanczos算法

n阶非对称矩阵A的特征值问题(如式(4)所示)的Lanczos算法［6］的主要思想是利用两组双正交向量将矩阵A逐次三对角化，得到一个ns(ns≤n)阶的三对角矩阵T，将矩阵T的特征值作为原矩阵A的ns个极大特征值的近似，将矩阵T的特征向量通过变换作为原矩阵A相应特征向量的近似。该方法最大的优势是大大减少了迭代次数，降低了存储代价。

为了求出矩阵A的前m个极小特征值，可做如下变换:的特征问题转化成求解如下的低阶特征问题:

经过以上过程，矩阵

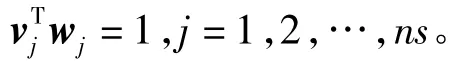
首先设定一小量ε，计算Gram－Schmidt系数:

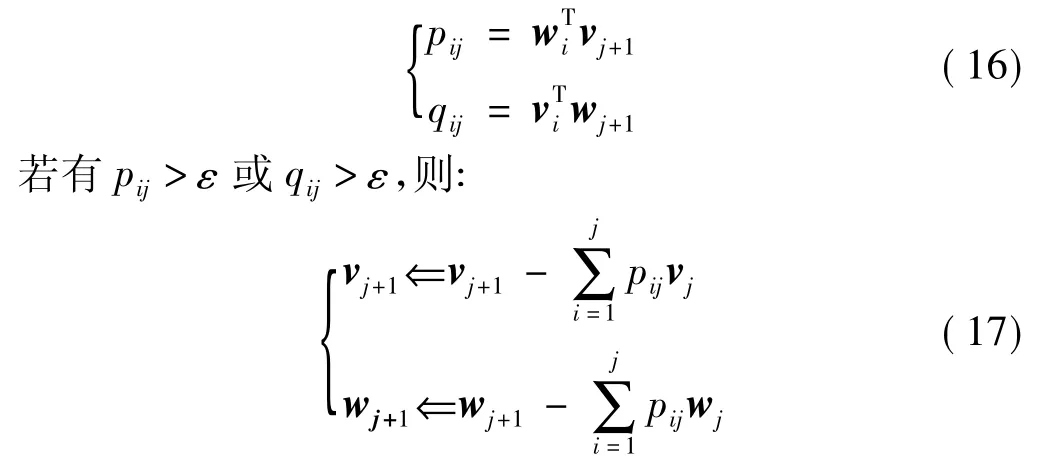
3 具有原点位移的双重步QR算法

具有原点位移的QR算法通过选取近似特征值作为位因子sk来提高QR算法的收敛速度。对于含复特征值的系统，采用双重步QR算法可以避免复数运算［7］，双重步QR算法的移位因子sk，sk+1可以通过求解系数矩阵T的右下角2×2阶子阵的特征值来获得，即:

由QR算法的性质，对于三对角矩阵T，迭代过程中产生的所有T(k)均为三对角矩阵［8］。迭代结束判定准则为出现次对角线元素 tl，l－1＜ ε(ε(tl，l+tl－1，l－1)(ε为设置的精度控制参数)。

(1)当l=m(m为T的阶数)时，T的一个高阶特征值可以由其最后一个主对角线元素获得;

(2)当l=m－1时，T的两个高阶特征值可以由其2阶后主子获得。

当求出若干个特征值后，矩阵收缩相应的阶数，迭代重新开始。通常迭代10次后还未确定出一个特征值时，可通过改变位移量来调整求解，一种可行的调整策略为:最后求得降阶后的矩阵T的所有特征值，i=1，2，…，ns。代入式(15)，即可得到矩阵T的所有特征向量 φt。

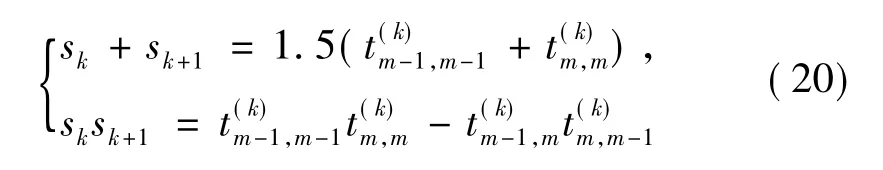
4 复特征向量的变换

5 标准特征值转化的分块Cholesky分解方法

对于标准特征值问题:

其一，若刚度矩阵K奇异，则无法进行求逆;

其二，直接求逆运算得到的矩阵严重不对称，会给数值计算中带来很大的舍入误差;

其三，对于大型矩阵，直接求逆运算的计算效率较低。

为了改善求解过程中的数值计算精度和效率，可以采用分块Cholesky分解来求出标准特征值问题的系数矩阵。

首先，为了避免矩阵K奇异，可引入移位因子α，得到非奇异矩阵～B:

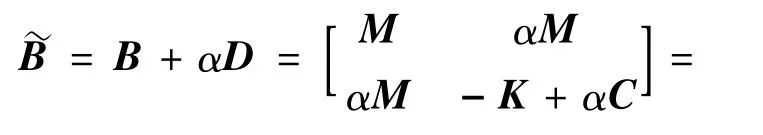
该方法只需要求两次Cholesky分解，一次下三角矩阵求逆，三次矩阵乘法即可得到矩阵A。对于奇异问题也只需要多进行两次矩阵减法。另一方面，该方法形成的系数矩阵近似反对称，便于进行压缩存储，也不会在计算过程中引入很大的范数误差，不需要再对系数矩阵进行平衡化处理，相当于减少了一个相似变换的过程。

6 Lanczos-QR算法实现

Lanczos-QR算法的主要思想是利用求解绝对值最小的特征值的逆幂法思想来改进截断格式的Lanczos方法降低矩阵阶数，得到一个包含原矩阵的低阶特征值的三对角矩阵，再使用带移位的双重步QR方法对降阶后的三对角矩阵进行全部特征值求解，以避免计算过程中的复数运算。

本文对算法进行了编程实现，程序采用科学计算程序FORTRAN语言进行实现。在程序设计中，遵循了以下的设计思想:① 设计中用子程序来分别实现各个功能，用主程序控制流程，这样使得算法思路很清晰，易于进一步的改进、优化;② 在程序中，设置了与现有有限元软件的数据接口，方便对其进行读取。

使用改进截断格式的Lanczos算法求解大型复特征值问题软件实现流程如下。

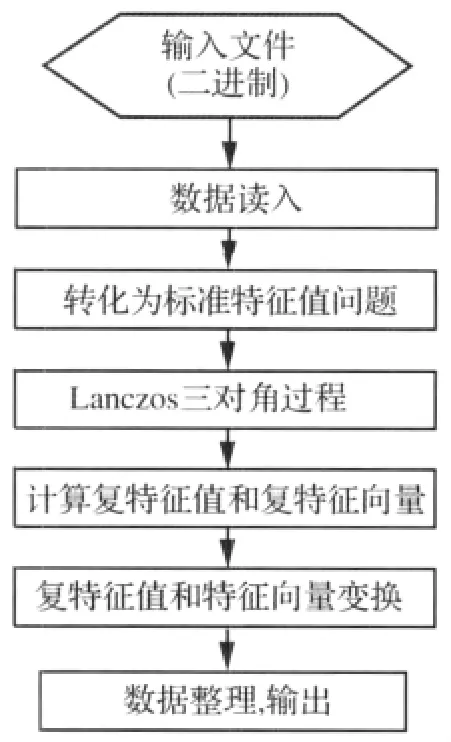
图1 程序设计流程图Fig.1 Programming flowchart

7 数值算例

7.1 约束阻尼梁

为了验证本文提出的算法在复特征值求解时的有效性和准确性，采用含粘弹性阻尼的约束阻尼结构来进行计算。如图2所示的约束阻尼悬臂梁，阻尼材料选用ZN－1型粘弹性材料。具体参数如下:

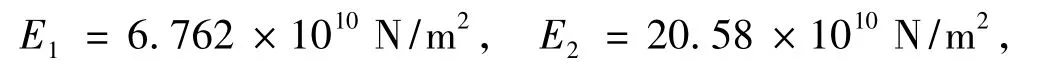
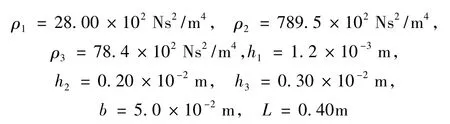
首先在MATLAB软件中建立该问题的有限元模型，单元类型及离散化方程可参见文献［10］。粘弹性阻尼等效使用文献［11］中所提到的Biot模型进行建模，经过等效之后得到复特征值问题。分别用MATLAB和本文算法求解，计算结果如表1所示。由表1中数据可见，与MATLAB结果相比，本文程序的计算结果具有很高的精度。

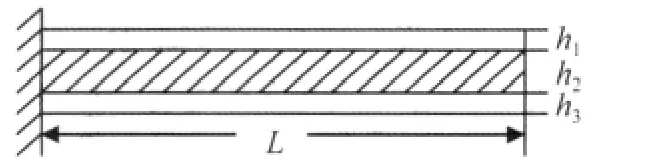
图2 约束阻尼梁Fig.2 A Sandwich Beam with Constrained Layer Damping

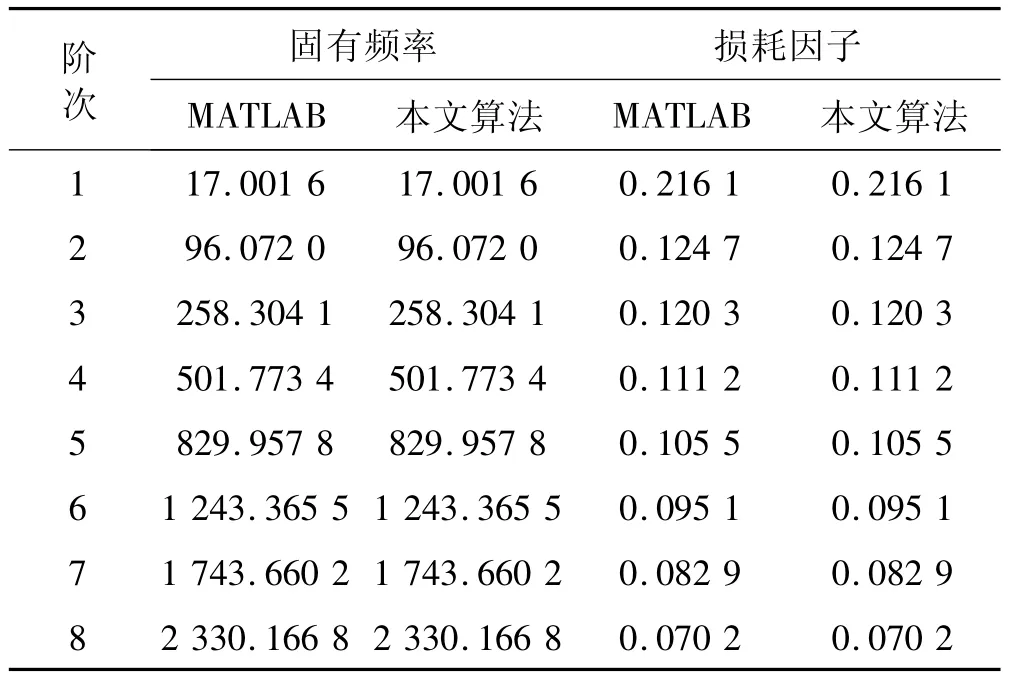
表1 频率和阻尼比计算结果Tab.1 Frequency and damping ratio results

7.2 大型卫星结构

该算例的目的是验证本文算法在求解大型结构时的精度。计算用卫星整体有限元模型(见图3)在大型有限元软件MSC/NASTRAN中建立。计算模型包括:节点:7162个;单元:9 964个;自由度:36 289个。具体材料参数与单元特性参数均由工程单位提供。

对底部进行约束，分别使用MSC/NASTRAN软件和本文程序计算得到整星前10阶固有频率，并与工程单位提供的卫星整星模型前四阶模态测试结果数据对比，结果如表2所示。结果表明本文程序在计算大型结构特征值问题中也是有效的。

图3 卫星有限元模型Fig.3 Satellite FEM model

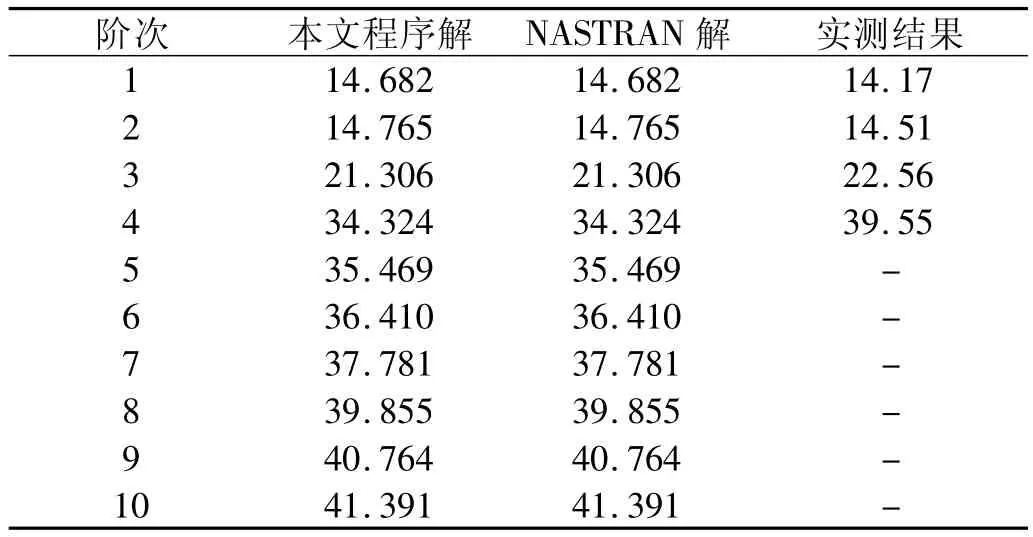
表2 频率计算结果Tab.2 Frequency results

8 结论

针对含有非比例阻尼的大型结构动力学分析中出现的大规模复特征值的求解问题，本文发展了适用于大规模非对称实矩阵的标准特征值问题的求解方法，该方法集合了Lanczos算法的高效率和QR算法的稳定性，可以有效解决大规模复特征值问题的求解。本文算法具有如下优点:① 采用分块矩阵的三角分解来对广义特征值问题进行标准化，可以避免大型矩阵求逆运算和非对称矩阵引起的舍入误差，从而可大大降低算法的计算量，并且明显改善了求解精度;② 可以通过人为设置控制求解精度，从而在效率和精度的矛盾中取得平衡。

本文还给出了使用此算法计算时的求解流程，并使用科学计算软件FORTRAN对该算法进行编程实现，对其模块化和软件化提供了算法支持，为开发有自主知识产权的有限元求解器奠定基础。实例证明了该算法对于大型非对称矩阵特征值问题是有效的和精确的。

［1］淡丹辉，孙利民.结构动力有限元分析的阻尼建模与评价［J］.振动与冲击，2007，26(2):121－125.

［2］荣见华，郑健龙，徐飞鸿.结构动力修改及优化设计［M］.北京:人民交通出版社，2002.

［3］宫玉才，周洪伟，陈 璞，等.快速子空间迭代法、迭代Ritz向量法与迭代 Lanczos法的比较［J］.振动工程学报.2005，18(2):228－232.

［4］张 琪.利用有限元和Lanczos法的细长弹体模态分析［J］.弹箭与制导学报，2007，27(4):61－63.

［5］王勖成.有限单元法［M］.清华大学出版社，2003.

［6］De Samblanx G，Bultheel A.Nested Lanczos:implicitly restarting an unsymmetric Lanczos algorithm［J］.Numerical Algorithms，1998，18:31 －50.

［7］ G.H.戈卢布，C.F.范洛恩.矩阵计算［M］.科学出版社，2001.

［8］A·R·高尔腊伊G·A·瓦特桑.矩阵特征值问题的计算方法［M］.上海科学技术出版社，1980，103－104.

［9］闫庆友，魏小鹏.求解大规模非对称矩阵特征问题的精化双正交Lanczos算法［J］.高等学校计算数学学报，2004，26(2):110－124.

［10］陈 前，朱德懋，周蒂莲.粘弹性阻尼结构的动特性分析［J］.航空学报.1986，7(1):37－45.

［11］ Zhang J，Zheng G T.The Biot Model and Its Application in Viscoelastic Composite Structures［J］.Journal of Vibration and Acoustics，2007，129(5):533 －540.

Application of lanczos-QR algorithm in large non-classical damping structures'modal analysis

ZHANG Jing1，LIU Ming-hui1，ZHENG Gang-tie1，2

(1.Harbin Institute of Technology，Harbin 150001，China;2.Tsinghua University，Beijing 100084，China)

Here，Lanczos-QR algorithm was introduced into the computation of a large complex eigenvalue problem.Combining efficiency of Lanczos algorithm and stability of QR algorithm，this method firstly reduced matrix scale with Lanczos algorithm，and then solved complex eigenvalues and complex eigenvectors of the reduced matrix with QR algorithm.In order to improve the algorithm's computing stability and precision，the partitioned matrix triangle decomposition was introduced to get a standard eigenvalue problem.A step-by-step procedure of this method was summarized and programmed with FORTRAN language.Numerical examples showed that the improved Lanczos-QR algorithm is precise and stable.

complex eigenvalue problem;non-symmetrical damping;Lanczos algorithm;QR algorithm

TB123;V414

A

国防科技工业民用专项科研技术研究项目(C4220061310)

2009－12－14 修改稿收到日期:2010－03－30

张 静 女，博士，1981年4月生