基于频响函数综合的舱筏隔振系统灵敏度分析和优化

黄修长，徐时吟，张志谊，华宏星

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

基于频响函数综合的舱筏隔振系统灵敏度分析和优化

黄修长，徐时吟，张志谊，华宏星

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

利用频响函数综合方法，推导了浮筏隔振系统连接点的位移，给出基座上的力和输入到基座的功率流对浮筏隔振系统的上、下层隔振器的刚度和阻尼的设计灵敏度表达式，并分别以最小化某一频段内输入到基座的功率流和传递到基座的力的均方值为优化目标，结合灵敏度分析方法，对上、下层隔振器的刚度进行了优化。优化结果表明，基于子结构灵敏度分析的方法是一种有效的优化方法，以最小化传递到基座的力的均方值为优化目标得到的隔振器的最优刚度不能同时使输入到基座的功率流有很大的衰减。

灵敏度分析和优化;频响函数综合;舱筏隔振系统

灵敏度是结构特征参数(特征值，特征向量和频响函数矩阵、阻抗矩阵)对结构参数(其它设计变量，如刚度，阻尼，局部质量和局部刚度)的改变率。进行灵敏度分析可以指导设计者如何修改结构参数，以使系统的总体动态特性改变最为有效。通过求得目标函数对参数的灵敏度，在灵敏度最大的方向进行搜索就可以最快的速度接近最优的目标。灵敏度方法由于概念清楚、使用方便，广泛应用于机械系统设计及模型修正中。

在工程中，常用的结构灵敏度分析有结构响应的灵敏度分析、结构特征值和特征向量的灵敏度分析［1］。在进行灵敏度分析时，采用的模型有解析模型、基于有限元分析得到的模态模型以及通过实验测得的频响函数模型。灵敏度的求解方法包括有限差分法(包括中心差分法以及向前差分法)、对设计变量直接求偏导的解析和半解析方法［2］。

基于频响函数综合的子结构方法是对组合结构进行建模的最有效方法之一。有许多学者使用频响函数综合方法推导了结构动力系统的灵敏度，并应用于工程问题中。Chang和Park［3］利用链式微分法则推导了多个子结构综合时的子结构导纳灵敏度，并成功用于结构的动力修正。Lee等人［4］利用基于频响函数的子结构方法对汽车的传动系统和副车架－弹性连接元件－车身结构进行了动力学建模，并对弹性连接元件的刚度和阻尼(弹性连接元件的阻抗数据采用试验手段获得)进行灵敏度分析，以某一频段内内部噪声最小为优化目标，求得满足约束条件下的最优值。在文献［5］中，Lee将该方法推广到了多个子结构相互连接的情况，利用子结构之间界面上的力对设计变量的直接偏导求得任意子结构的响应的灵敏度。在Lee的方法中，需要对整个结构的频响函数矩阵进行求逆，容易产生数值误差。从他们的研究中可以得出两点结论:①基于子结构灵敏度分析的方法不需要进行模态分析，可直接利用导纳数据进行分析;② 导纳数据可以是实测的导纳数据或者是通过计算得到(有限元)的导纳数据。

国内一些研究者针对浮筏隔振系统的建模和优化也做了许多研究。徐张明［6］利用ANSYS和SYSNOISE对浮筏隔振系统的振动和声辐射响应进行计算，求得浮筏隔振系统中结构声学频响函数的灵敏度，并以要求得到的频响函数为目标函数，以支撑刚度为设计变量，对隔振系统进行了优化设计。吴广明［7］提出了一种新的利用子结构的模态参数进行建模的子结构方法，并在这个方法的基础上推导了隔振系统功率流的灵敏度，给出一种新的将遗传算法和灵敏度分析相结合的混合遗传算法，以输入到基座的功率流为目标，对隔振系统的上、下层隔振器的刚度和阻尼进行了参数优化设计。

本文在上述研究的基础上，采用基于频响函数综合的子结构方法对浮筏隔振系统进行建模，将由动力设备－浮筏装置－艇体组成的复杂系统分解为若干个子结构。在建模中，将浮筏弹性体和艇体弹性基础的子结构以频域中的频响函数模型表示，其中频响函数模型可以通过数值方法或者解析方法计算得到，也可以从试验数据中获取，同时利用阻抗矩阵表示隔振器动态模型，最后运用基于子结构的频响函数的综合方法得到系统总的频响函数矩阵。在这种建模方法的基础上，本文推导了浮筏隔振系统子结构中连接点的位移，给出基座上的力和输入到基座的功率流对子结构动态参数(如刚度和阻尼)的灵敏度表达式，并利用灵敏度对子结构动态参数进行约束条件下的多目标多参数优化。本文方法的优点是，需要求逆的矩阵维数大大降低，仅对包含界面自由度的频响函数矩阵求逆，并通过SVD分解减小数值病态，计算量大大减少。

1 基于子结构的导纳灵敏度方法

本节从基于频响函数的子结构方法出发，推导结构响应对子结构动态参数的灵敏度表达式。浮筏隔振系统由机组，上层隔振器，浮筏，下层隔振器和基础组成，其中基础为带内部基座的加筋圆柱壳体。基座连接点受到由机组激励引起的动态力的作用，最终导致圆柱壳体振动。在对浮筏隔振系统利用基于频响函数的子结构方法进行建模时，需要进行两次子结构综合，即先对浮筏和基础进行综合，再进行基础－浮筏综合体和机组刚体的综合，分别如图1(a)和图1(b)所示。

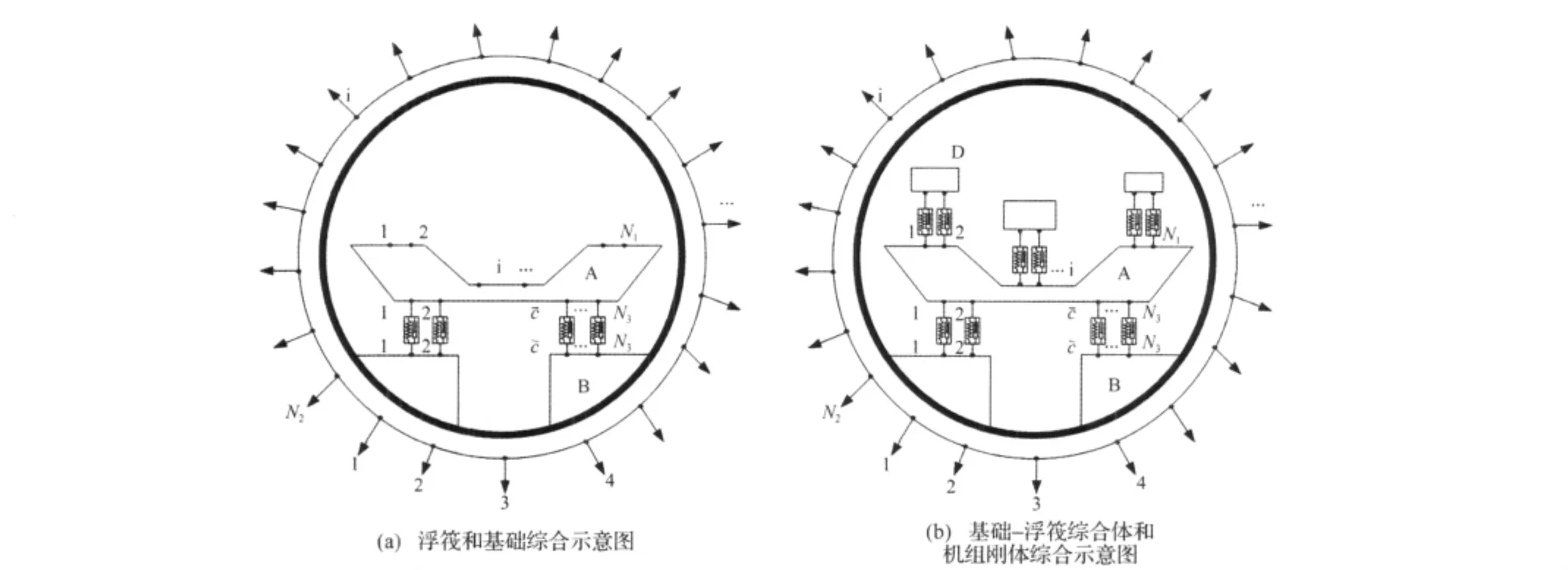
图1 (a)浮筏和基础综合示意图;(b)基础－浮筏综合体和机组刚体综合示意图(图中A代表浮筏子结构，B代表基座子结构，D代表机组子结构，N1为上层隔振器的数目，N3为下层隔振器的数目，i代表综合时的内点，c代表浮筏上的连接点，代表基座上的连接点)Fig.1(a)The synthesis process of raft and base;(b)The synthesis process of raft-base and machine)(A:raft;B:base;D:machine.N1:number of upper springs;N3:number of lower springs.i:internal points;c:coupling points on raft;coupling points on base)

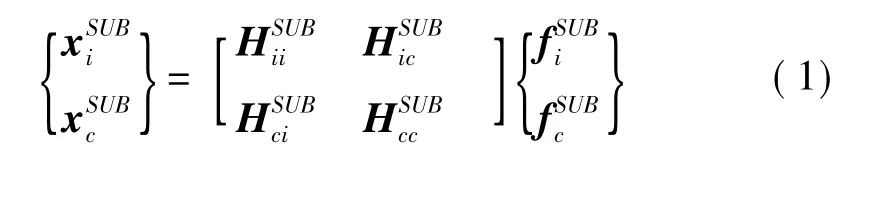
在每次综合时，假设浮筏，基座和机组上与该层隔振器相连的点为连接点，不与该层隔振器相连的点为内点，对于浮筏，基座和机组，其频响函数表达式为:其中:x代表位移向量，f代表力向量，H为对应点与点之间的频响函数矩阵，下标i表示内点对应的频响函数，下标c表示连接点对应的频响函数。上标SUB为A时代表浮筏子结构，为B时代表基座子结构，为D时代表机组子结构。

对于隔振器，采用阻抗矩阵表示如下:

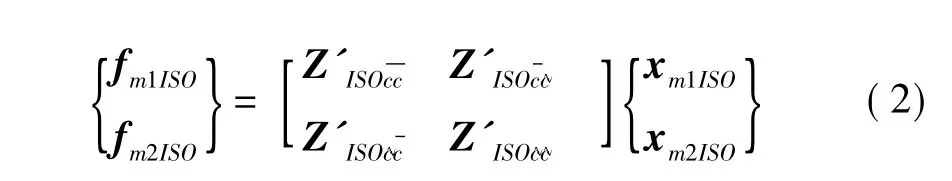
其中:x代表位移向量，f代表力向量，Z为阻抗矩阵，下标表示隔振器的上部连接点，下标表示隔振器的下部连接点。下标ISO为1时代表下层隔振器，为2时代表上层隔振器。考虑隔振器安装的角度，通过变换矩阵可以得到:

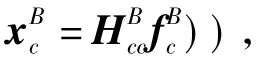
在进行基座－浮筏综合体和机组刚体的第2次综合时，机组上的质心点作为机组的内点，外力通过刚体的平移旋转矩阵转换到机组质心;基座－浮筏综合体的内点是浮筏下部以及基座上的下层隔振器的连接点，机组和基座－浮筏综合体通过上层隔振器连接起来。由频响函数综合的结果可知浮筏－基座的综合体和机组的综合结果为:

其中每个子矩阵可以由频响函数的综合结果得到。假设只有机组上有外力作用，对应于，其他子结构上没有外力作用，并且外力和结构参数没有关系，则浮筏和基座位移对应的子矩阵是:

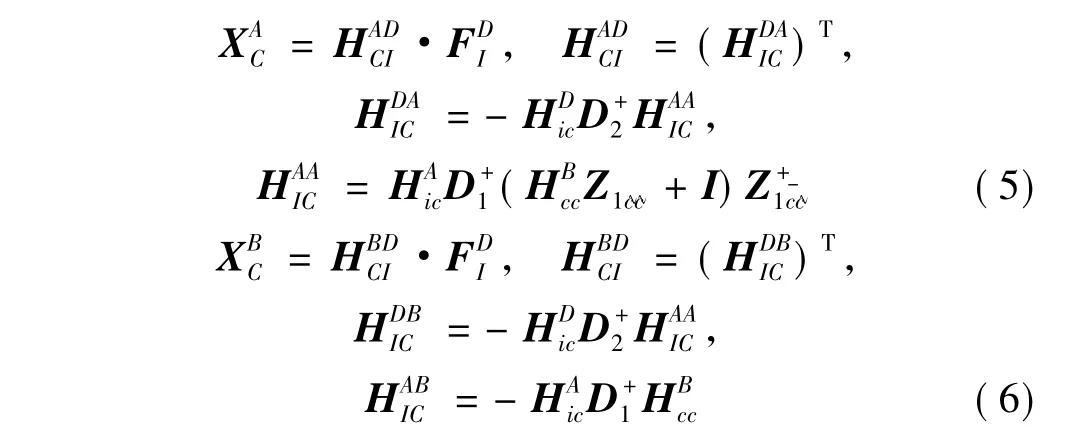
由(5)可以得到浮筏下部连接点对上、下层隔振器刚度的灵敏度表达式为:

假设隔振器阻抗矩阵采用刚度k和结构阻尼系数η表达，即:

2 以振动传递特性、功率流为目标的舱筏声学性能优化设计

功率流同时考虑了传递到基座的力以及激起的速度响应的影响，从能量的角度更加全面地评价隔振系统的性能;此外，声辐射的能量在基座结构没有阻尼的情况下取决于输入到基座的能量的大小，因此对输入到基座的功率流进行优化可以减少声辐射的能量。另一方面，低频时线谱对远场声压的贡献很大，而传递到基座的力是直接影响到远场声辐射的激励，因此减小激励力所对应的频率处输入到基座的力可以减少该频率线谱的声辐射。因此本文分别以某一频段内输入到基座的功率流最小和传递到基座的力的均方值最小为优化目标，结合灵敏度分析方法，对上、下层隔振器的刚度进行了优化。将指定的正弦激励频率段离散成m个激励频率点，要求在此频段内传入基础的功率流为Pi之和极小或者传递到基座的力的均方值极小，同时满足相应的静力和动力约束条件，其优化模型可以由下式表达:

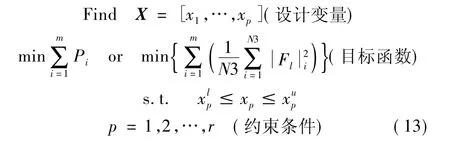
式中xp为设计变量，可为隔振器刚度、隔振器阻尼等，和分别为xp的下限和上限。利用以上的灵敏度分析的方法，沿着灵敏度方向进行搜索就可以最快的方向得到最优的目标值。

3 数值验证

对一双机组浮筏隔振系统(图2)，利用本文提出的灵敏度分析方法求解灵敏度，和有限中心差分法的结果进行对比，并利用求得的灵敏度进行参数优化。

该浮筏隔振系统机组1和2的质心为坐标分别为(0，1.0，1.0)和(0，1.0，2.0)，质量为 499 kg，转动惯量为(13.3，13.3，13.3)，每个机组下面的隔振器数目为 4个，浮筏与基座之间的隔振器数目为6个，上、下层隔振器的刚度均为2×106N/m，3×106N/m，结构阻尼系数为0.02，隔振器的连接点位置如表1所示。基座和浮筏的频响函数是由ANSYS计算得到的模态叠加得到，假设激励施加在机组1的点(0，1.2，1)上，沿着全局坐标系的y方向，大小为1 N。由于浮筏隔振系统的能量主要通过垂向力传递，因此本文仅考虑垂向自由度。

图2 数值算例示意图Fig.2 Model for numerical simulation

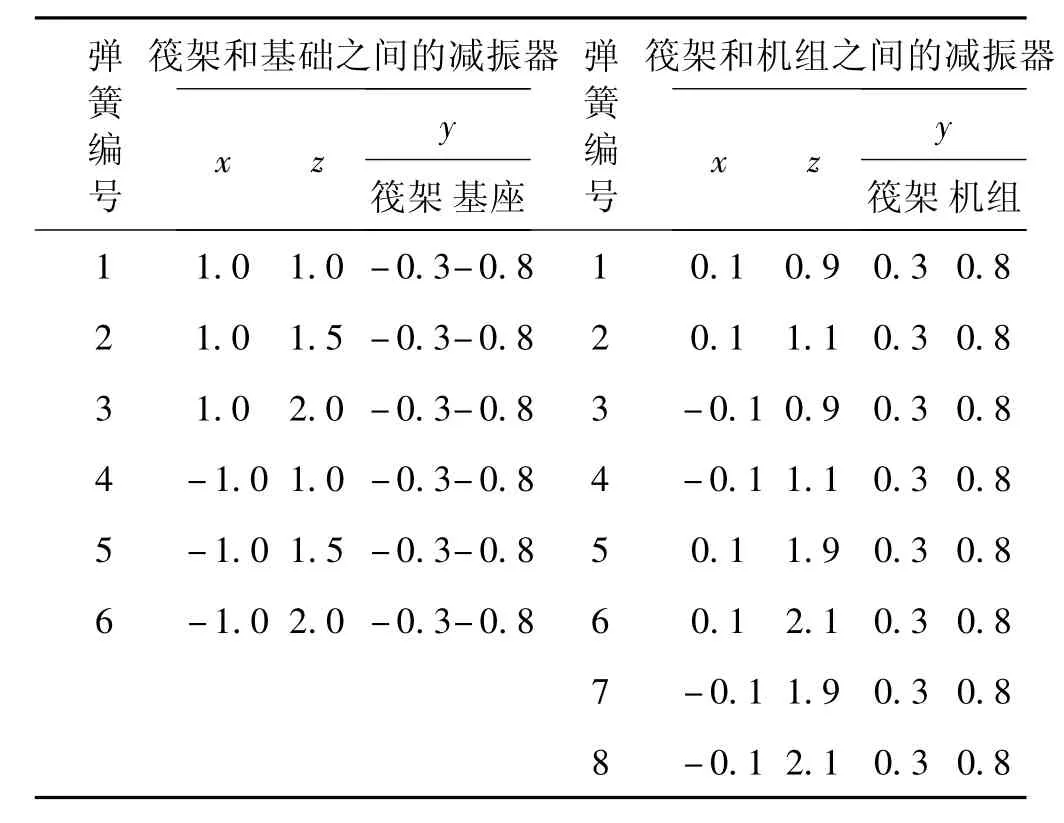
表1 隔振器参数Tab.1 Parameters for lower and upper springs

将子结构导纳灵敏度的结果和直接由向前有限差分法求得的灵敏度的结果进行比较，以下给出部分结果(图3－图4)，所有的结果中，带◇的结果为有限中心差分法计算得到的结果。

基于图2所示的模型，由于激励力的频率为25 Hz，分别以21 Hz－31 Hz之内输入到基座的功率流最小以及传递到基座的所有力的均方值最小为优化目标，设计变量为上下层隔振器的14根弹簧的刚度，并且假设上、下层隔振器的刚度值的变化范围不超过目前刚度值的10%。优化结果显示，在以输入到基座的功率流最小和以传递到基座的所有力的均方值最小为优化目标的优化迭代过程中，分别迭代了24次和13次。图5－7给出了设计变量的变化趋势图以及优化目标的变化趋势图。

从以上优化结果可以看出，总体趋势是下层隔振器的弹簧越软，传递到基座的均方力和输入到基座的功率流均向着降低的方向移动，这和以前的许多研究结果是一致的［6，7］。对于上层隔振器，弹簧编号为1－4的弹簧是和激励机组相连的，编号为5－8的弹簧是和另外一个非激励机组相连。在两种优化情况下，与激励机组相连的弹簧的刚度值越低，输入到基座的功率流和传递到基座的均方力均越小，与非激励机组相连的弹簧的刚度值越高，输入到基座的功率流和传递到基座的均方力均越小，这和［7］的研究结果是一致的:此时非激励机组相当于整个浮筏隔振系统的一个动力吸振器，非激励机组与浮筏的连接弹簧的刚度值越大，由［7］，输入到非激励机组的功率则越大，由能量守恒，传递到基座的功率会降低。

图8给出了在初始刚度和两种优化情况下的最优刚度时，在0 Hz－150 Hz之内输入到基座的功率流和传递到基座的所有力的均方值随频率的变化趋势。从图中可以看出:以输入到基座的功率流最小为优化目标时，输入到基座的功率流在所要求优化频段内会大大降低，但是在其他频段内会恶化，以传递到基座的所有力的均方值最小为优化目标得到的隔振器的最优刚度值不能使得输入到基座的功率流有很大的降低。以传递到基座的所有力的均方值最小为优化目标时，传递到基座的所有力的均方值在所有频段内会大大降低，但是在优化频段内以输入到基座的功率流最小为优化目标得到的隔振器的最优刚度值能够提供更优的结果。并且在所允许的刚度值范围内，对浮筏隔振系统固有频率(即功率流的峰值)的影响不是很大。

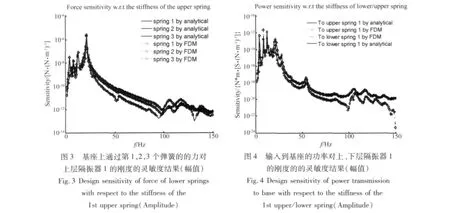
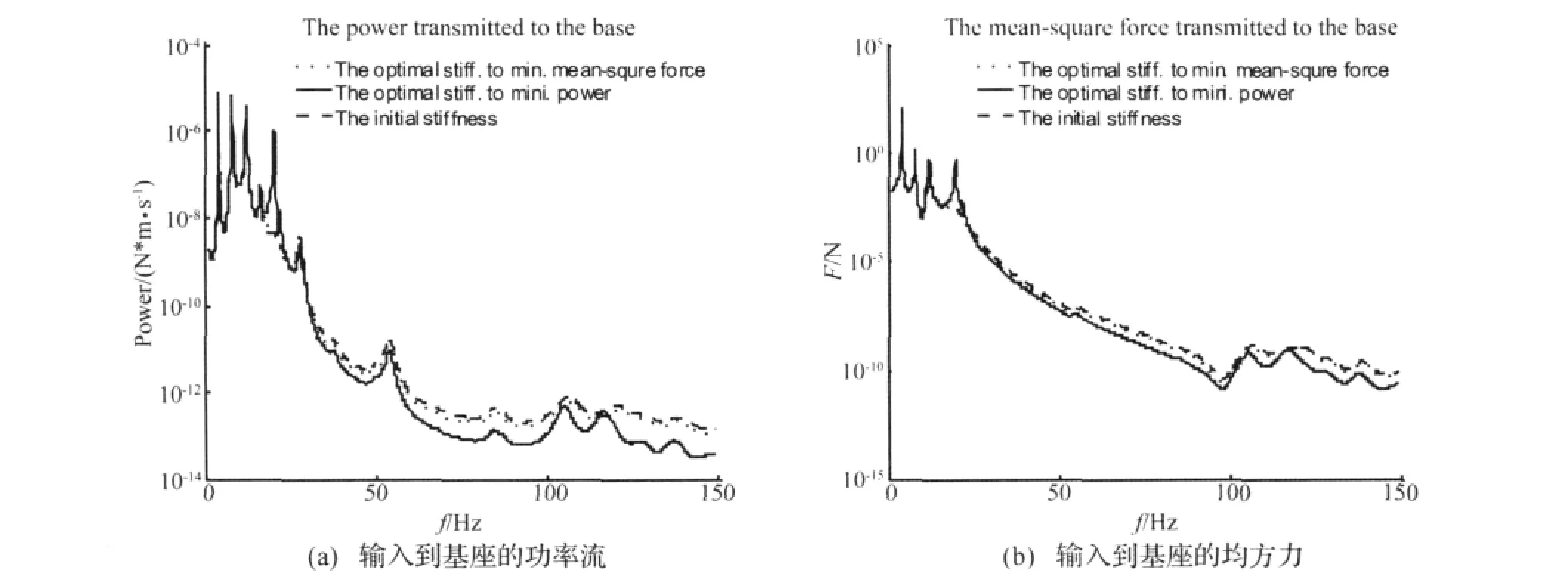
图8 三种刚度情况下0 Hz－150 HzFig.8(a)Power transmission to base between 0－150Hz(b)Mean－square force transmitted to base between 0－150Hz

4 结论

本文给出了一种基于子结构频响函数矩阵的子结构导纳灵敏度方法，详细推导了浮筏隔振系统子结构中连接点的位移、通过隔振器的力、输入到基座的功率流等对结构参数的灵敏度矩阵表达式，并结合灵敏度分析对结构参数进行有约束条件下的多目标多参数优化。

通过推导和分析，可以得出基于子结构的导纳灵敏度方法具有以下优点:

(1)基于子结构的灵敏度分析方法不需要进行模态分析，直接对导纳数据进行分析;

(2)导纳数据可以是实测的导纳数据或者是计算得到(有限元)的导纳数据;

(3)该方法将隔振器采用阻抗矩阵单独表示，在综合时求逆的矩阵维数大大降低，仅需要对包含界面自由度在内的频响函数矩阵求逆，在进行灵敏度分析时仅需要对隔振器进行求偏导，大大减小了计算量。

分别以某一频段内输入到基座的功率流最小和传递到基座的最大的力最小为优化目标，结合灵敏度分析方法，对一个典型浮筏隔振系统的上、下层隔振器的刚度进行了优化。利用以上的灵敏度分析的方法，沿着灵敏度方向进行搜索就可以最快的方向得到最优的目标值。研究结果表明子结构导纳灵敏度方法是一种有效的优化方法。

［1］傅志方，华宏星.模态分析理论与应用［M］.上海:上海交通大学出版社，2000.

［2］ Choi K，Kim N.Structural sensitivity analysis and optimization［M］.Springer，2005.

［3］ Chang K J，Park Y P.Substructural dynamic modification using component receptance sensitivity［J］.Mechanical Systems and Signal Processing，1998，12:525－541.

［4］ Lee D，Hwang W，Kim C.Design sensitivity analysis and optimization of an engine mount system using an FRF-based substructuring method［J］.Journal of Sound and Vibration，2002，255(2):383－398.

［5］ Lee D H，Hwang W S.Parametric optimization of complex systemsusing a multi-domain FRF-based substructuring method［J］.Computers＆ Structures，2003，81(22 －23):2249－2257.

［6］徐张明.带浮筏装置的水中壳体模型振动声辐射及其结构参数灵敏度研究［D］.上海:上海交通大学，2003.

［7］吴广明.舰船复杂隔振系统建模及其功率流研究［D］.上海:上海交通大学，2004.

［8］ Liu W，Ewins D J.Substructure synthesis via elastic media［J］.Journal of Sound and Vibration，2002，257(2):361－379.

Design sensitivity analysis and optimization of a floating raft system using a FRF-based substructuring method

HUANG Xiu-chang，XU Shi-yin，ZHANG Zhi-yi，HUA Hong-xing

(State Key Laboratory of Mechanical System and Vibration，Shanghai Jiaotong University，Shanghai 200240，China)

A general method for design sensitivity analysis of forces and power flow of base in a typical floating raft system was presented using a FRF-based substructuring formulation.The proposed method gave an expression of design sensitivity in terms of partial derivatives of physical parameters of upper and lower isolators as well as transfer functions of substructures.An optimization scheme involving the derived sensitivity formula was used to obtain optimal physical parameters of isolators of the floating raft system to minimize the mean-square forces transmitted to the base and the timeaveraged power flows to the base，respectively.The simulation results demonstrated that the proposed method is efficient and accurate，and minimization of force transmissibility does not certainly provide a minimum power flow.

sensitivity analysis and optimization;FRF-based substructuring method;floating raft system

TB535

A

十一五预研项目资助

2009－12－15 修改稿收到日期:2010－11－04

黄修长 男，博士生，1983年10月生