含裂纹悬臂梁的振动与疲劳耦合分析

刘文光 ，陈国平

(1.南京航空航天大学 航空宇航学院，南京 210016;2.南昌航空大学 航空制造工程学院，南昌 330063)

含裂纹悬臂梁的振动与疲劳耦合分析

刘文光1，2，陈国平1

(1.南京航空航天大学 航空宇航学院，南京 210016;2.南昌航空大学 航空制造工程学院，南昌 330063)

基于Paris方程和同步分析方法考虑振动与疲劳裂纹扩展耦合之影响，提出一种含裂纹梁的振动疲劳寿命分析思路。振动分析过程中，利用线性弹簧等效裂纹段，复弹性模量引入阻尼损耗因子，得到考虑裂纹扩展、激励频率和阻尼等因素影响的动应力响应。结果表明:裂纹扩展、激励频率和阻尼等因素对疲劳寿命具有重要的影响。通过振动分析与疲劳裂纹扩展寿命估算同步进行，可进一步提高疲劳寿命估算精度。

振动疲劳;分段分析;裂纹扩展;裂纹悬臂梁

绝大多数工程结构在使用过程中都不可避免要受到振动载荷的作用，诸如飞机、火箭、汽车、化工容器以及建筑桥梁，等等。振动不仅影响工程结构的正常工作，还会引起振动疲劳破坏，严重地影响结构的安全可靠性，直接威胁人类的生命安全，并造成重大的经济损失。因此，一般的工程结构都把抗振动疲劳作为结构的重要设计准则。

梁是工程中广泛使用的一种结构，由于各种原因导致梁不可避免地存在各种损伤，大部分以裂纹的形式存在。长期处于振动环境中，结构裂纹会不断扩展并导致断裂。为保证裂纹不发生疲劳失效，必须对工程结构进行定期检查。生产实际中，通常根据经验确定裂纹可检测长度，而非靠预测方法来确定。

随着断裂力学的发展，提出了很多估算疲劳寿命的方法［1－3］。已知裂纹位置的名义应力或应力场，就能确定从起始裂纹扩展到某一临界值所要经历的振动次数。然而，尽管裂纹扩展是因强迫振动引起，疲劳寿命分析中仍然采用静力学方法计算应力，应力被内在地假定与激励频率、阻尼无关，且常忽略裂纹扩展引起的动响应变化。工程实际中，大量结构服役于宽频激励的振动环境中，使结构可能一直处于共振状态并导致共振疲劳。由于涉及振动响应，所以研究此类问题时必须考虑阻尼和激励频率对疲劳寿命的影响。

为此，有关激励频率对结构振动疲劳寿命的影响已有不少研究［4～9］。例如，1981年 Valanis利用内时理论推导了结构疲劳寿命与加载频率之间的关系;1993年毛罕平和陈翠英推导了全面反映加载频率影响的裂纹扩展速率公式。随后，Dentsoras和Kouvaritakis研究了轴向共振条件下激励频率对聚合物材料疲劳裂纹扩展寿命的影响;Shih和Chen分析了激励频率对304不锈钢疲劳裂纹扩展速率的影响，并提出一种考虑激励频率的疲劳裂纹扩展模型。

但是，上述研究只考虑了激励频率的影响，忽略了阻尼以及裂纹扩展对疲劳寿命的作用。另外，由于裂纹扩展会改变结构动态特性，所以结构动响应分析时也须考虑裂纹扩展与振动的耦合作用。

因此，本文在结构振动分析时，考虑裂纹扩展对振动的影响，得到考虑激励频率、结构阻尼以及裂纹扩展的动态应力;基于Paris方程和同步分析方法使振动分析与疲劳寿命估算同步进行，进一步提高结构疲劳裂纹扩展寿命估算精度。

1 振动分析

1.1 结构裂纹的处理

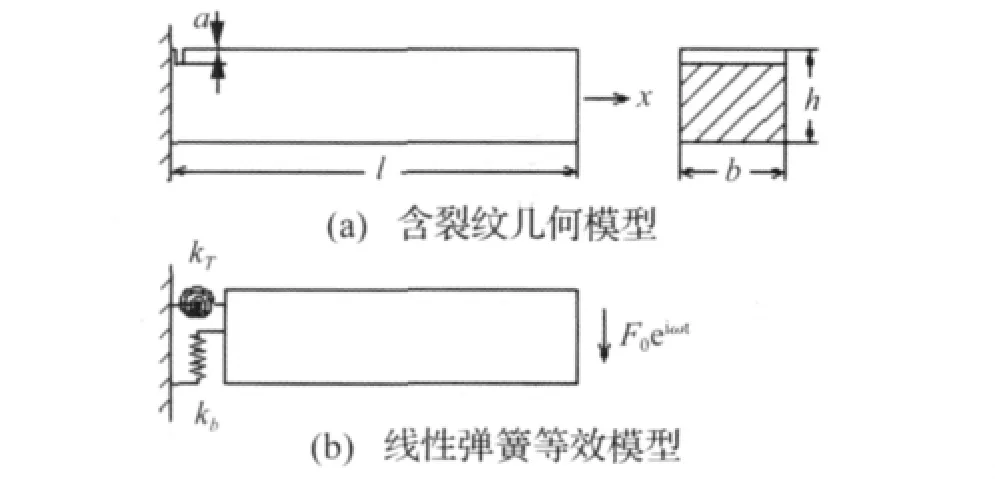
图1 裂纹梁振动系统 (梁长l，宽b，高h，裂深a)Fig.1 Cracked Cantilever Beam(Length:l，Width:b;Height:h;Crack Depth:a)

图1(a)所示为受横向加载的单边裂纹悬臂梁。在横向简谐振动载荷作用下，裂纹扩展会引起结构单元刚度发生退化，并改变其动态特性［10］。为便于结构动力学分析，需要对结构裂纹作近似处理。通常采用线性扭转弹簧与拉压弹簧等效裂纹段，如图1(b)所示。等效弹簧的刚度由结构材料、裂纹类型以及裂纹位置等参数确定。根据断裂力学的方法［13］，可推导结构裂纹引起的局部柔度

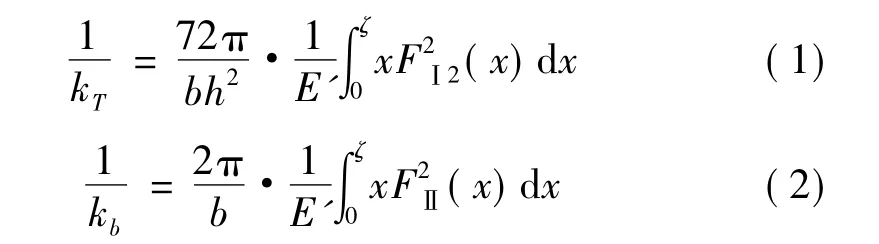
式中:kT为扭转刚度;kb为拉压刚度;FⅠ2(x)为I型裂纹修正系数;FⅡ(x)为Ⅱ型裂纹修正系数;ζ=a/h为相对裂纹深度;E'=E/(1－v2)对应于平面应变情况。

根据裂纹类型以及加载形式［11］，裂纹修正系数为:

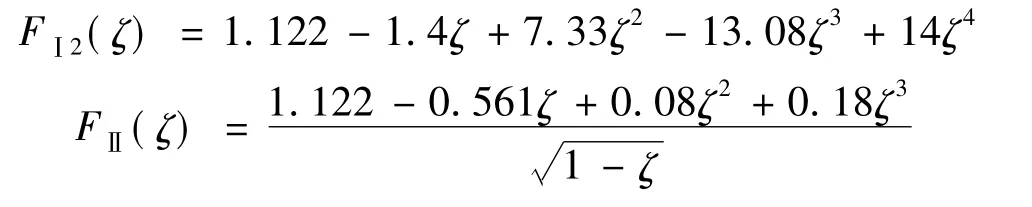
将上述裂纹修正系数分别代入公式(1)和(2)，可得到等效弹簧刚度的具体表达式。通过变刚度可以把裂纹扩展引进到结构振动分析中。

1.2 结构振动分析

结构共振时，振幅及内力值等骤增，此时必须考虑阻尼的影响。若采用复数阻尼理论，则等截面梁弯曲自由振动微分方程为:

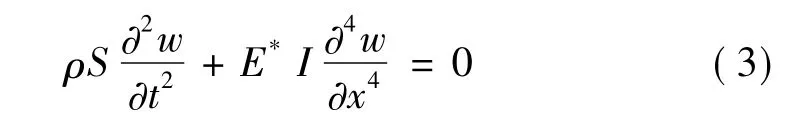
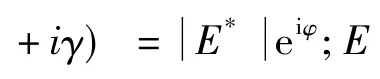
如图1，当裂纹在结构根部时，结构自由振动边界条件修改为:

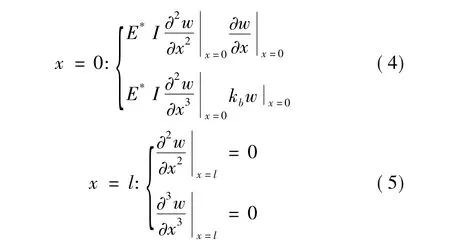
根据以上边界条件得到考虑裂纹扩展变化的修正的固有频率方程:

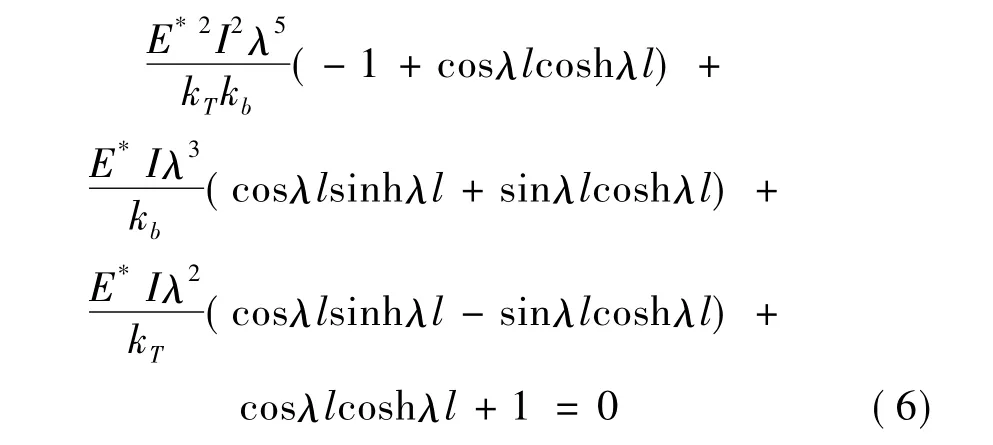
求解上述方程时，弹性模量只取其中的储能模量部分。方程(6)表达了结构固有频率与裂纹深度之间的一一对应关系，对结构裂纹的监测具有十分重要的理论意义。

横向力激励下，结构强迫振动边界条件应修改为:

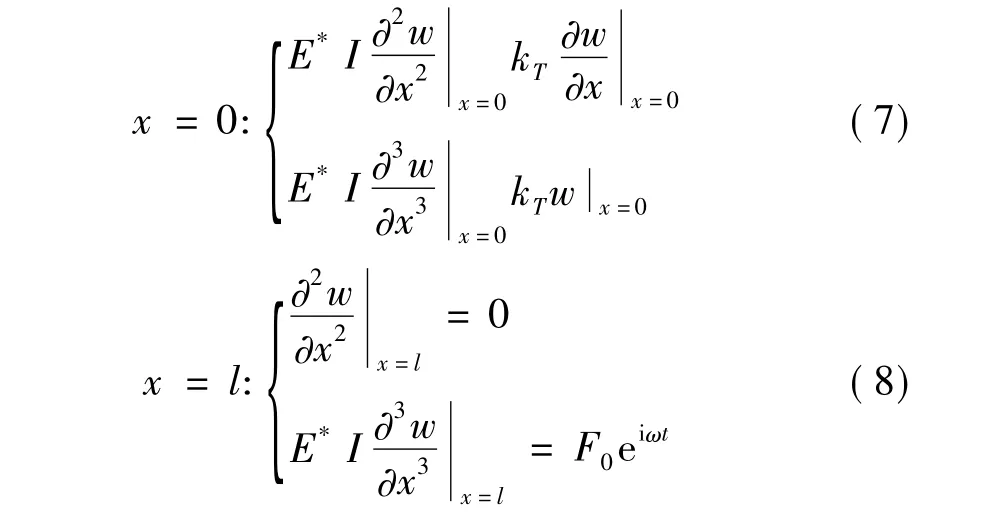
根据上述边界条件可求得结构位移响应:

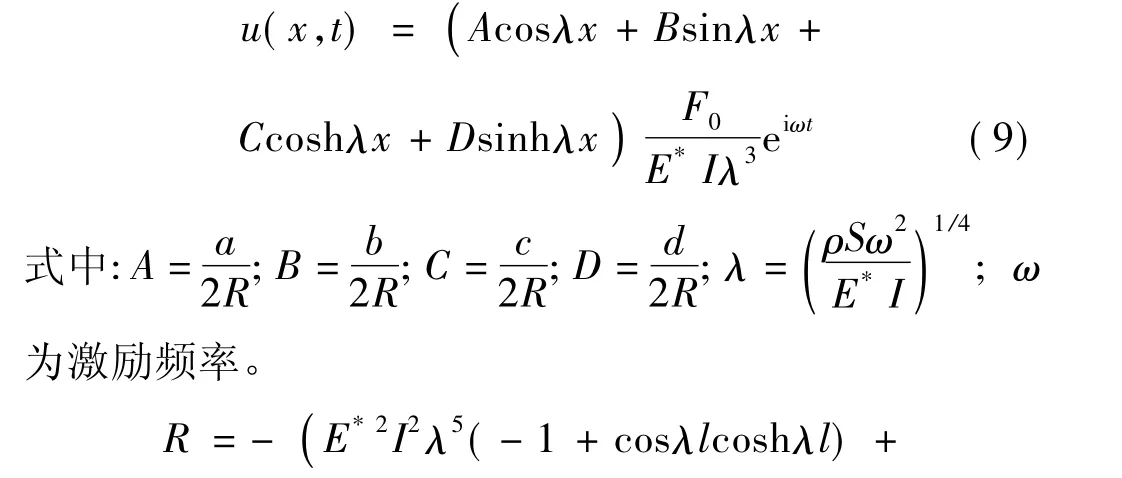
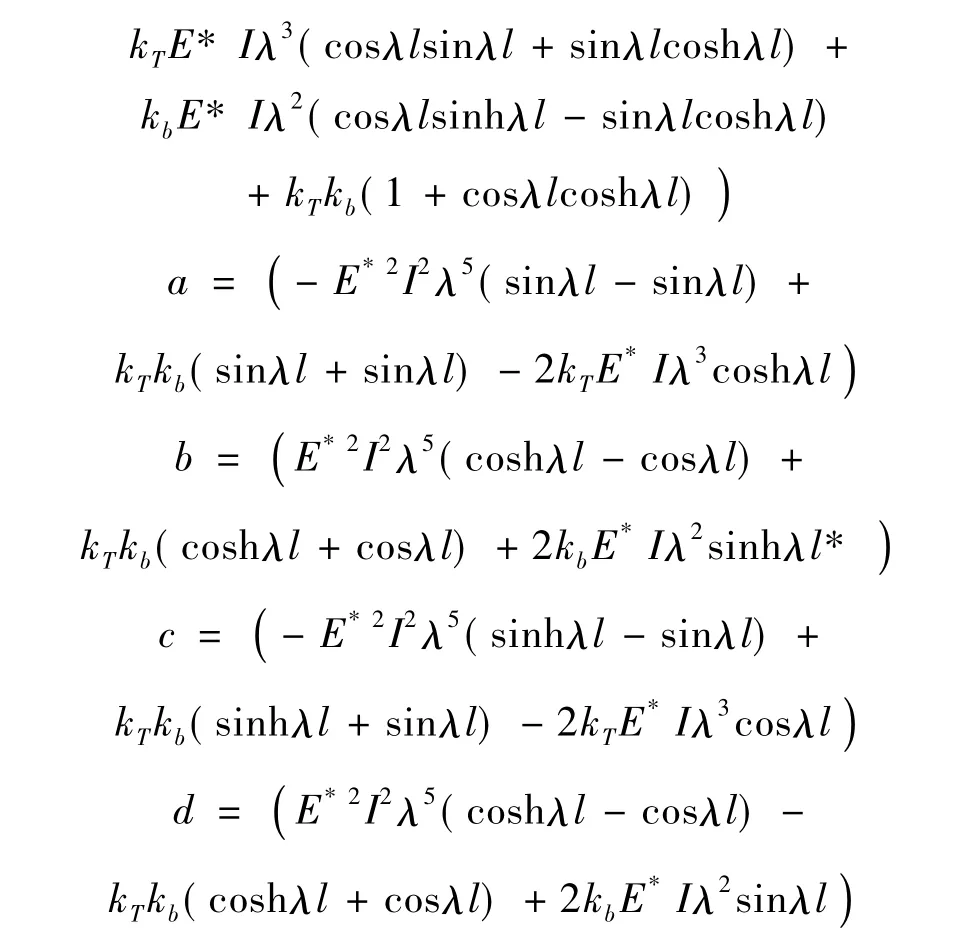
由于Ⅰ型裂纹是工程中最常见的裂纹形式，且其破坏程度比较严重，故以Ⅰ型裂纹为研究重点。根据HOOKE定律得到结构动应力响应:

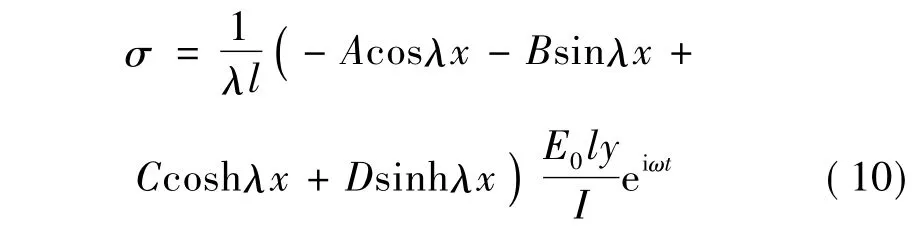
结构裂纹位置的动应力表达式为:

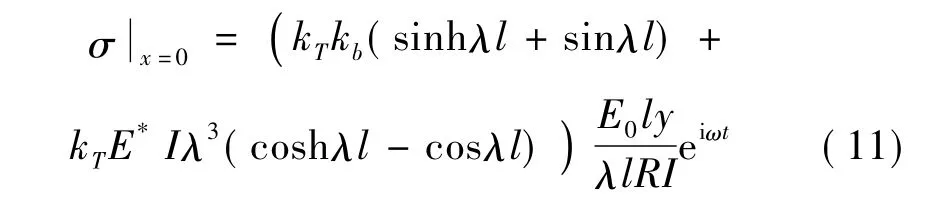
按静力学方法，激励频率为0时应力为σ0=F0ly/I，则最大动应力可表示为:

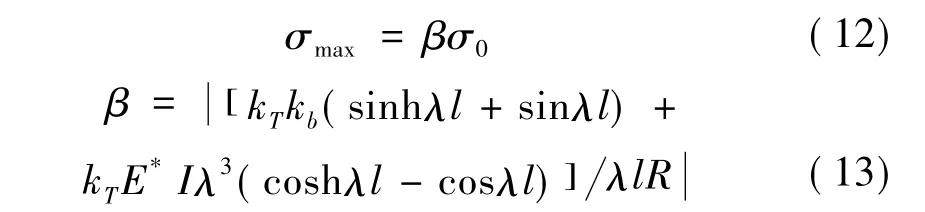
式中:β为动应力放大系数，它反映了激励频率、结构阻尼以及裂纹扩展对动应力的影响。

2 结构振动疲劳裂纹扩展

2.1 动应力强度因子的确定

动应力强度因子KI是振动载荷作用下表征裂纹尖端应力场分布的物理量，通常而言，动应力强度因子与裂纹长度的关系可按下式确定:

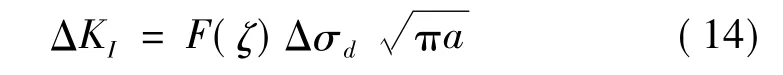
式中:F(ζ)为裂纹修正因子;Δσd为动应力振幅;ΔKI是动应力强度因子的振幅。

假设加载为脉动循环，裂纹为开放式裂纹，则动应力强度因子可表示为:

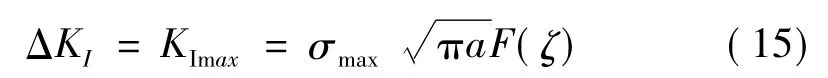
把公式(12)代入公式(15)并依据裂纹及加载类型，可得到考虑裂纹扩展、激励频率和阻尼综合作用的动应力强度因子

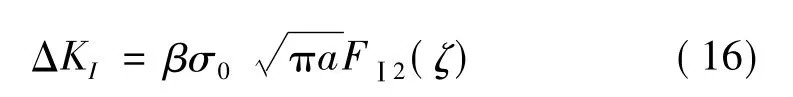
2.2 振动疲劳裂纹扩展速率方程

研究表明，在中等应力状态且平均应力很低时，使用Paris方程［12］能很好地描述直裂式裂纹的疲劳扩展速率。Paris方程表示式如下:

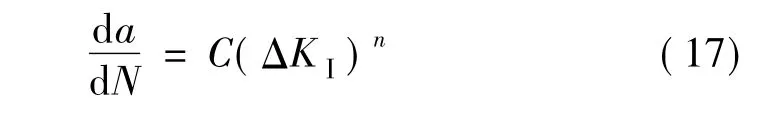
式中:C，n是材料常数;其余参数同上述公式。

把动应力强度因子表达式(16)代入Paris方程得到振动疲劳裂纹扩展速率模型:

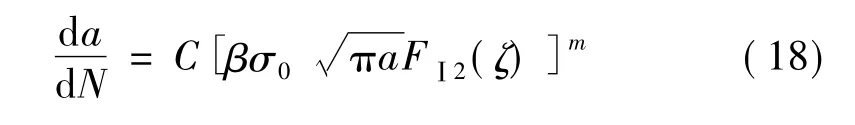
2.3 振动疲劳裂纹扩展分析

相同结构内含不同大小的裂纹时，其动态特性必然不同，必定改变结构的动应力响应并导致裂纹尖端应力场强发生变化。分析认为:结构振动会引起裂纹扩展，而裂纹扩展也会改变结构振动特性，进而影响裂纹扩展特性，两者之间存在耦合关系。传统的疲劳裂纹扩展理论却忽略了这种耦合作用。为此，本文采用同步分析方法，使结构振动分析与疲劳裂纹扩展寿命估算同步进行，考虑耦合作用对疲劳裂纹扩展寿命的影响，进一步提高疲劳寿命估算精度。

动应力作用下，不能直接采用Paris方程估算结构疲劳寿命。为此，必须采用同步分析近似处理。具体做法是，把每振动一周得到的动应力幅值近似为恒定值，代入公式(20)积分得到每振动一次产生的裂纹扩展量。结构受到变振幅载荷的作用时，最终的裂纹深度可由叠加法计算，表示如下:

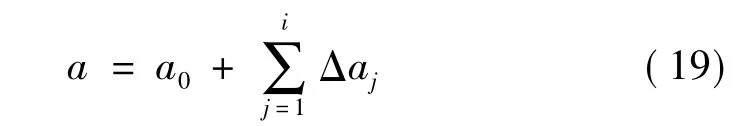
式中，a0为初始裂纹深度;Δaj是第 j次循环的裂纹增量;i为总振动循环次数;a为振动i次后的裂纹总深度。

利用公式(18)积分可计算恒幅值激励下结构疲劳裂纹扩展增量:

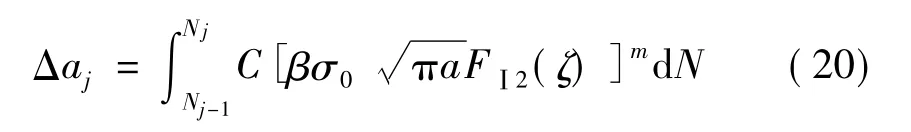
振动循环的增量可表示为:

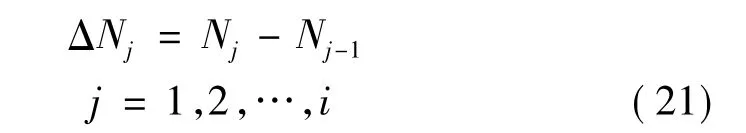
考虑 ΔNj很小(本文取 ΔNj=1)，则:

因此，在裂纹中心点的裂纹扩展量可被方程式(23)近似计算出:

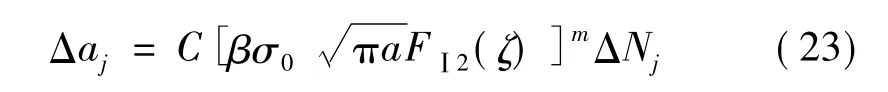
2.4 疲劳裂纹扩展失效判据

为了判断结构是否失效，文中采用以下判据

准则1:如果结构裂纹扩展至梁的中面就认为结构已经破断，此时裂纹的扩展不再适合用裂纹尖端的SIF来进行估算。

式中:ac为临界裂纹长度，本文取ac=h/2。

准则2:如果裂纹尖端应力强度因子大于材料的断裂韧性时，则认为结构发生失稳断裂。

式中:Kmax为最大应力强度因子;KC为材料断裂韧性。

3 结构振动疲劳分析算例

假设结构几何尺寸 l=300 mm、h=20 mm、b=2 mm;材料为AISI1050低碳合金钢［14］，材料参数为E=2.1E11Pa、ρ=7 860 kg/m3、σb=723.45E6、KC=1.172 2 E9 N/m3/2、ΔKth=9.3241E5 N/m3/2;试验常数为 C=3.0 093E －32、m=3.3。初始裂纹深度 a0=2 mm;计算步长取ΔN=1周;激励幅值为50 N，保持不变。

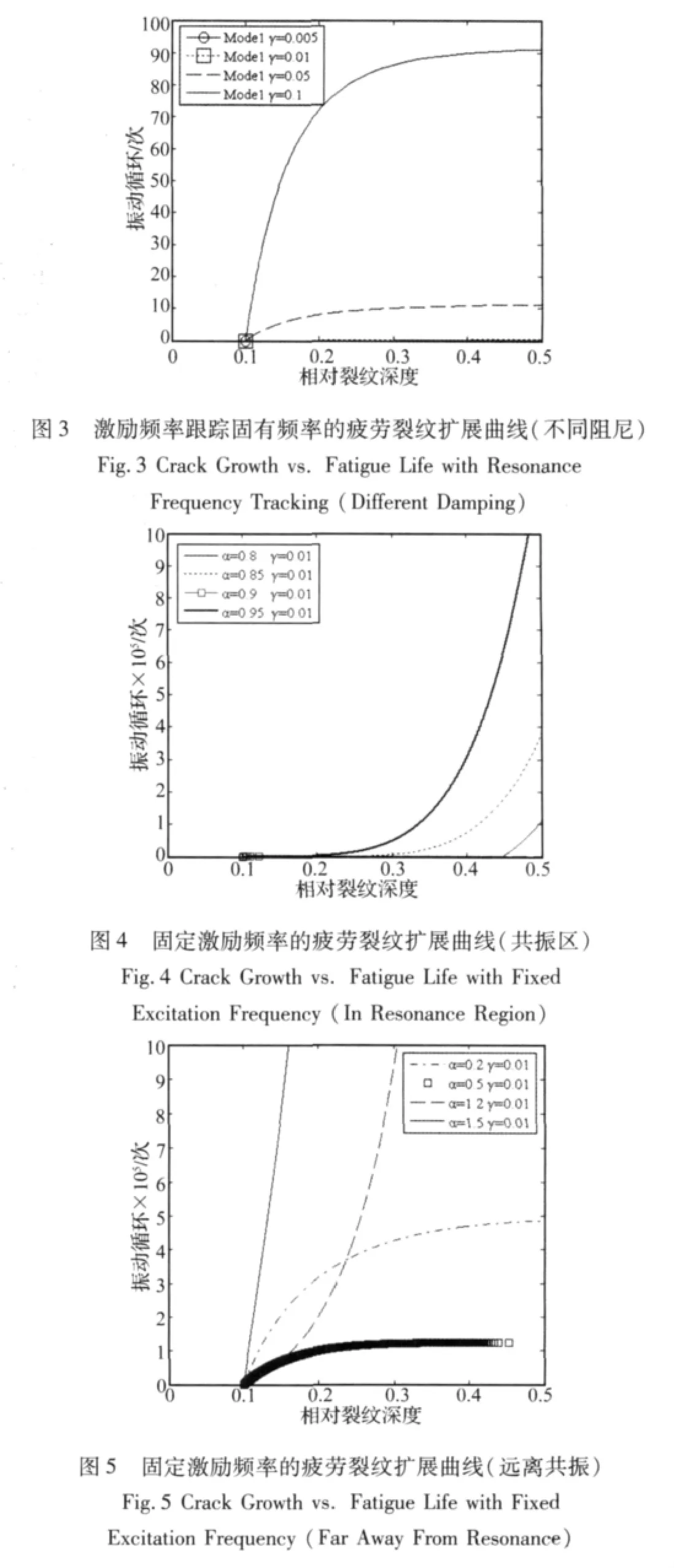
强迫振动分为共振和非共振两种形式，影响其破坏的主要因素也有所变化。图2～图5分别表明了激励频率跟踪结构固有频率、共振区固定激励频率、非共振区固定激励频率三种激励状态下结构振动循环次数与裂纹扩展之间的内在规律。结果表明，激励频率和阻尼对结构疲劳寿命具有重要的影响，在共振环境下尤其明显。相同幅值的外部激励作用下，第一阶模态共振引起的疲劳破坏更为严重，小阻尼对疲劳裂纹扩展速率影响不是很明显。激励频率跟踪结构固有频率时的结构疲劳寿命远远小于其它强迫振动下的结构疲劳寿命。固定激励频率时，激励频率越接近结构固有频率，结构疲劳裂纹扩展寿命越短。图4、图5中α表示激励频率与无裂纹结构第一阶固有频率之比。

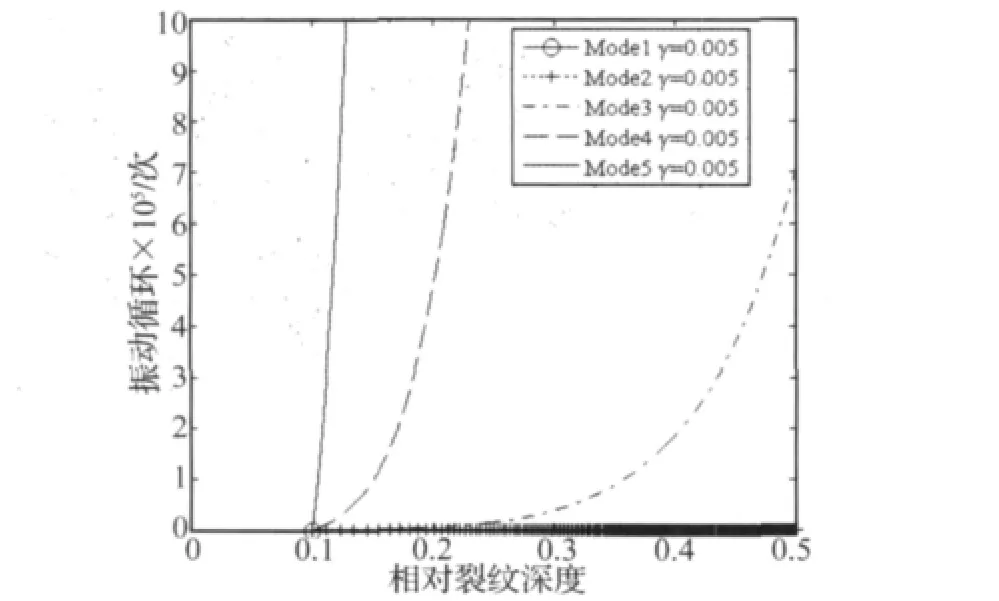
图2 激励频率跟踪固有频率的疲劳裂纹扩展曲线(不同模态)Fig.2 Crack Growth vs.Fatigue Life with Resonance Frequency Tracking(Different Mode)

4 结束语

为便于分析，用线性弹簧近似取代裂纹单元、复弹性模量引入阻尼;通过结构振动分析，得到考虑裂纹扩展、阻尼以及激励频率等影响的动应力，与常规疲劳裂纹扩展分析相比，应力的计算更符合实际;基于疲劳裂纹扩展方程和同步分析方法，考虑振动与裂纹扩展的耦合关系对疲劳寿命的影响，使振动分析与疲劳裂纹扩展寿命估算同步进行，提出了一种含裂纹结构的振动疲劳分析思路，进一步提高结构疲劳寿命估算精度。分析结果表明，裂纹扩展、结构阻尼以及激励频率对疲劳寿命具有重要的影响，在共振区尤其明显;跟踪第一阶共振频率的结构疲劳裂纹扩展过程十分迅速，小阻尼对疲劳扩展影响不显著;跟踪固有频率的结构疲劳裂纹扩展寿命远小于其它强迫振动作用下的结构疲劳裂纹扩展寿命;远离共振环境后，阻尼对结构疲劳裂纹扩展寿命的影响可以忽略不计，但疲劳裂纹扩展速率随激励频率离固有频率越近疲劳寿命越短。

［1］Ponomarev P V，Lopatin A D.Calculation of the fatigue fracture underthe influence ofdynamic loads［J］.International Applied Mechanics，1972，8(6):613 －617.

［2］Shih Y S，Wu G Y.Effect of vibration on fatigue crack growth of an edge crack for a rectangular plate ［J］.International Journal of Fatigue，2002，24:557 566.

［3］Schlums D H.Fatigue testing and crack analysis of resonating structures［D］.Swiss Federal Institute of Technology Zurich，2001.

［4］Yeh J T，Hong H S.Effect of branch frequency on dynamic fatigue behavior of slowly notched polyethylene polymers［J］.Journal of Polymer Research，1994，4(1):375－383.

［5］ Dentsoras A J，Kouvaritakis E P. Effects of vibration frequency on fatigue crack propagation of a polymer at resonance ［J］.Engineering Fracture Mechanics，1995，50(4):467－473.

［6］ Valanis K C.On the effect of frequency on fatigue life［C］.Presented at the winter annual meeting of the American Society ofMechanicalEngineering， Washington D.C，November，1981:15 －20.

［7］ Shih Y S，Chen J J.The frequency effect on the fatigue crack growth rate of 304 stainless steel［J］.Nuclear Engineering and Design，1999，191:225 230.

［8］毛罕平，陈翠英.考虑动应力时加载频率对裂纹扩展速率的影响［J］.江苏工学院学报，1993，14(6):26－33.

［9］沈 为，高大兴，蒋松山，等.加载频率对疲劳裂纹扩展速率的影响［M］.武汉:湖北人民出版社，1980，2:186－195.

［10］ Papaeconomou N，Dimarogonas A.Vibration of cracked beams［J］.Computational Mechanics，1989，5:88 －94.

［11］Tada H，Paris P C，Irwin G.R.The stress analysis of cracks handbook ［M］.DelResearch Corporation Hellertown，Pennsylvania.1973.

［12］ Paris P C， Erdogan F. A criticalanalysisofcrack Propagation laws［J］.Journal of Basic Engineering，1963，85:528－534.

［13］ Ewalds H L，Wanhill R J.Fracture mechanics［M］.Edward Arnold Ltd，1984.

［14］ Dentsoras A J，Dimarogonas A D.Resonance controlled fatigue crack propagation in a beam under longitudinal vibration ［J］.International Journal of Fracture，1983，23:15－22.

Coupling analysis for vibration and fatigue of a cracked cantilever beam

LIU Wen-guang1，2，CHEN Guo-ping1

(1.College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 20016，China;2.School of Aeronautical Manufacturing Engineering，Nanchang Hangkong University，Nanchang 330063，China)

An analytical method about vibration and fatigue of a cracked cantilever beam was proposed based on timing analysis and Paris equation.Coupling relationship between vibration and fatigue crack growth was considered by using timing analysis methods.Crack part was replaced with a linear spring and damping loss factor was introduced with complex elastic modulus during vibration analysis.So crack growth，excitation frequency and damping were considered in vibration analysis.Results indicated that crack length，excitation frequency and damping have important effects on the fatigue life of the beam;in the resonance region，the rate of crack growth is obvious and the speed decreases with increase in damping.The prediction precision of fatigue life could be further improved using this new analytical method.

vibration and fatigue;piecewise analysis;crack propagation;cracked cantilever beam

V216.3;V224

A

南昌航空大学校基金资助(EC200906236)

2009－12－02 修改稿收到日期:2010－03－22

刘文光 男，博士生，讲师，1978年5月生