基于ICMCM法的GARTEUR结构有限元模型修正研究

王金明，李伟明，彭明峰

(上海航天精密机械研究所，上海 201600)

基于ICMCM法的GARTEUR结构有限元模型修正研究

王金明，李伟明，彭明峰

(上海航天精密机械研究所，上海 201600)

改进的正交模型正交模态(ICMCM)法在进行模型修正过程中需要同时使用实验测得的频率及模态振型等数据。本文利用有限元模型的模态振型代替实验测量的模态振型并通过迭代解决了模型修正过程中缺少实验模态振型数据的问题，使ICMCM法具有更广的应用范围。根据国际认可的三级评价标准使用ICMCM法对GARTEUR飞机模型进行了修正，并与国际上其他单位的模型修正结果进行横向比较，结果证明了本文改进方法的可行性及修正结果的优越性。

有限元法;模型修正;GARTEUR模型;迭代

为了能够方便、快捷的掌握工程结构的动力学特性，研究人员大多采用对其建立有限元模型进行分析。现阶段，航天器、桥梁等特殊用途的工程结构对有限元模型的精度及可靠性提出了更高的要求。但是，由于有限元建模过程中不准确的模型简化以及材料、几何参数的不确定性等因素造成有限元模型的计算结果与实验样机的测试结果之间往往存在着较大的差距，使得根据工程图纸和经验建立的有限元模型并不可靠，这时就需要利用模型修正技术来修正结构的有限元模型，提高其精度及可靠性［1－4］。

从1958年Gravitz［5］为解决飞机地面共振实验中测量振型的正交化问题，提出依据实验数据修正飞机结构的柔度矩阵以来，有限元模型修正技术取得了飞速的发展。目前有限元模型修正方法主要分为矩阵型模型修正方法和参数型模型修正方法两大类，其中参数型模型修正方法由于其修正结果具有明确的物理意义并且便于大型工程分析软件利用，因此受到越来越多的重视。2007年，Hu等［6］提出了一种参数型的模型修正方法，称为正交模型正交模态法(Cross-model cross-mode method，简称CMCM法)，该方法不需要进行灵敏度分析并且具有良好的建模误差判断能力。另外，CMCM法不需要将实验模态与有限元模态进行一一配对，在修正过程中实验模态可以与任意一阶有限元模型的模态进行组合，增加了修正方程的数量，从而极大地增加了修正参数的个数。然而李剑等人［7］指出在有限元模型计算得到的模态振型与实验测量得到的模态振型相关性很好的情况下，CMCM方法容易在求解过程中出现分母为零或近似为零的情况而造成数值病态问题，并对CMCM法进行了改进，提出了改进的正交模型正交模态法(Improved cross-model cross-mode method，简称ICMCM法)。使用ICMCM法进行模型修正，需要同时使用有限元模型与实验模型的频率及模态振型数据，然而复杂结构的模态实验有时很难测量得到理想的模态振型数据，因此就会造成模型修正中缺少实验数据的问题，这种情况下就无法使用ICMCM法进行模型修正。

为了能够对模型修正的质量进行评估，Link和Friswell［8］提出了评价模型修正效果的准则，对于频率可以简化为以下三条:① 修正后的有限元模型必须能够准确地复现所使用频段范围内实验模型的频率;②修正后的有限元模型应当能够预示修正所使用频段范围以外实验模型的频率;③ 修正后的有限元模型能够准确预示实验模型结构修改后的动力学特性，此处仅对实验模型进行修改，有限元模型不重新进行修正，而是在上一步修正的基础上根据实验模型的结构修改情况做出相应的结构调整，获得模态参数。

GARTEUR飞机模型是由法国国家航空航天研究院设计制造并由多家机构先后进行了多次动力学实验［8］，目前该结构已成为国际公认的用于评估动力学实验与模型修正技术的基准模型［8－10］。本文首先解决ICMCM法因缺少实验数据而无法进行模型修正的问题，然后根据上述的三条模型修正评价标准并通过具体的实验数据对GARTEUR飞机模型进行模型修正，最后与国际同行的修正结果进行横向比较，验证了ICMCM法以及本文所提出方法的优越性及可行性。

1 ICMCM法

假设有限元模型与实验模型的系统矩阵之间存在如下关系

其中:K*和M*分别为实验模态的刚度矩阵和质量矩阵;K、M为有限元模型的刚度矩阵和质量矩阵，Kn、Mn分别为有限元模型第n个子单元的刚度矩阵、质量矩阵对系统整体矩阵的贡献;αn、βn分别为第n个单元的刚度修正因子及质量修正因子，Ne表示有限元模型单元的个数。

Hu等［6］对特征方程考虑实验模态与有限元模态的混合加权后得到:

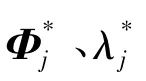
CMCM法在公式推导过程中采用式(2)除以式(3)的方法得到修正方程。但是，当有限元模型的模态振型与实验模型测量得到的模态振型之间相关性较好时容易在修正公式中出现分母为零或者近似为零的情况而造成数值病态问题。李剑等［7］对此做出改进，使用式(2)减去式(3)并利用式(1)，经过整理得到:

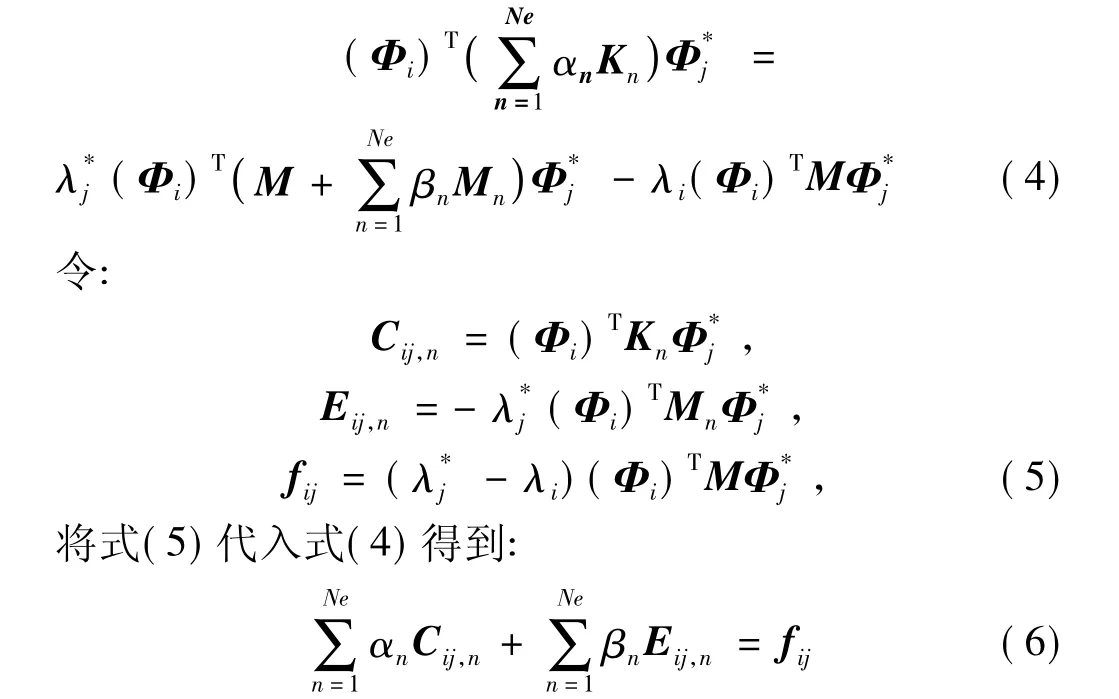
假设使用的有限元模态为nf阶，实验模态为nt阶，则式(6)代表了nf×nt个线性方程。对式(6)进行求解得到参数修正量αn及βn，然后通过式(1)获得修正后的有限元模型。通过对CMCM进行改进得到的新的模型修正方法称为ICMCM法。

使用ICMCM法进行模型修正时，需要同时使用有限元模型与实验模型的频率及模态振型数据，然而对于复杂结构的模态实验有时很难测量得到实验模态数据，因此就会造成模型修正过程中缺少实验数据的问题。为了解决该问题，本文采用传统的模态扩展方法，即直接使用有限元模型的模态振型Φ代替实验测试得到的模态振型Φ*，并通过迭代来不断的修正临时使用的模态振型，通过这种迭代过程不但可以解决缺少实验数据的问题而且还可以避免自由度匹配的过程，极大的增加模型修正方程的个数，进而增加修正参数的数量。具体的迭代过程如图1所示，其中ωk+1与Φk+1为第k次迭代过程中计算得到的有限元模型的频率及模态振型。

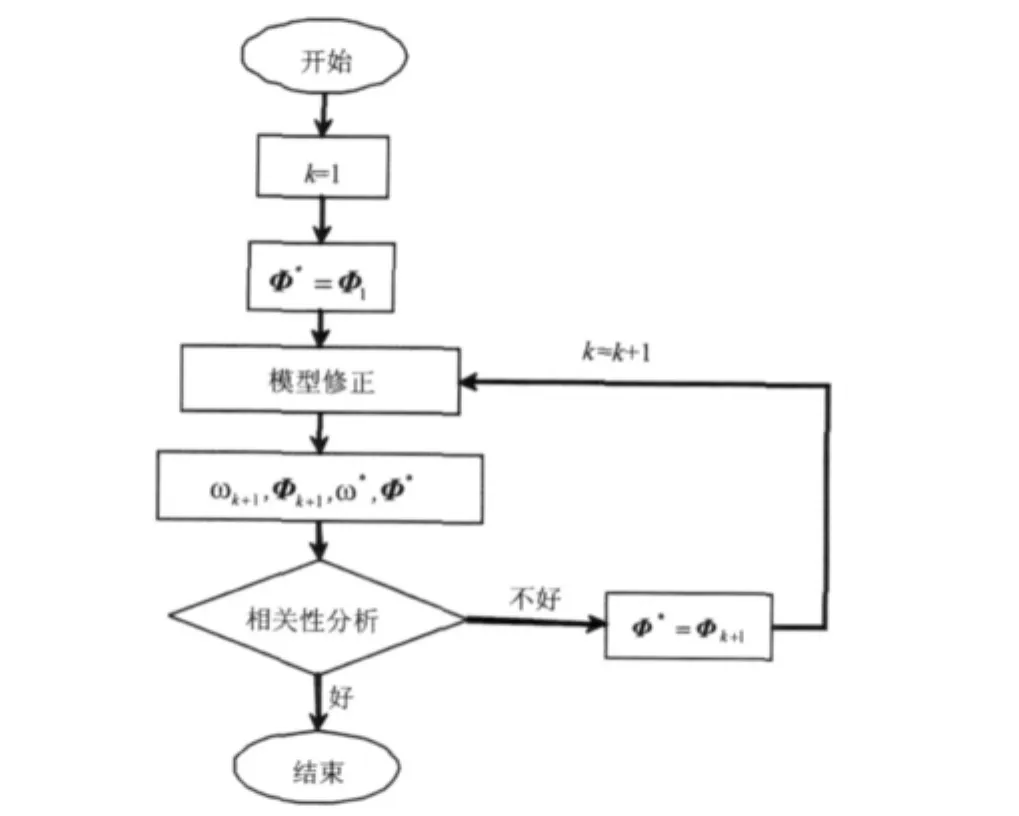
图1 模型修正流程图Fig.1 Simulation procedure of model updating

2 GARTEUR飞机模型有限元模型修正

GARTEUR飞机模型是具有12个成员的欧洲航空科技研究组织结构与材料工作组建立的一个典型的标准飞机模型，该项目启动于1995年由法国国家航空航天研究院设计制造并由多家机构先后进行了多次动力学实验。该飞机模型具有真实飞机的高柔度、模态频率低且密集的特点，目前已经被欧洲航空科技组织作为评估实验分析技术与模型修正技术的基准模型。该模型机身全长1.5 m，翼展2 m，结构总重44kg。为了增加机身阻尼，机翼上附着了一层1.1×76.2×1 700 mm3的粘弹性阻尼层，如图2所示。

为了能更深入的评价有限元模型修正的效果，Link和Friswell［8］详细介绍了两种对于初始GARTEUR飞机模型的局部修改的情况，如图2所示。修改1为在飞机的水平尾翼上增加一个0.92 kg的集中质量;修改2为用0.72 kg的黄铜代替飞机机翼左侧翼尖的0.15 kg的集中质量。对初始GARTEUR模型的结构修改对于评价有限元模型修正的结果以及评价模型修正参数的准确性具有重要的价值。GARTEUR模型小组对初始模型以及两种修改后的模型分别进行了高精度的模态实验。初始模型共测量得到14阶频率及模态振型，其中在模型修正过程中仅使用前9阶实验数据，后5阶实验数据根据模型修正评价标准的第二条校核修正后有限元模型的准确性;两种结构修改的目的为根据模型修正评价标准的第三条，分别使用结构修改后实验测得的前10阶数据，对上一步修正后有限元模型的可靠性做进一步检验。

2.1 对初始GARTEUR结构模型的修正

本文利用Ansys软件对GARTEUR飞机结构建立有限元模型，如图3所示。有限元模型含有50个节点，49个梁单元，2个集中质量，共51个单元，300个自由度，有限元模型总重42.339 kg。使用梁单元模拟机身与机翼、机身与垂直尾翼、垂直尾翼与水平尾翼以及机翼与左右两小翼之间的复杂连接，然后将Ansys软件建立的模型导入到Matlab软件中进行模型修正。修正前有限元模型频率与实验实测频率的对比见表1。由表1可以看到，初始有限元模型的前9阶频率最大误差为7.335 3%，平均误差为4.596 4%，后5阶频率的最大误差为5.985 1%，平均误差为2.947 2%，这说明由于GARTEUR结构的复杂性及参数的不确定性，造成了有限元建模的困难，导致有限元建模结果与实验测试结果相差较大，需要使用模型修正技术提高有限元模型的精度及可靠性。

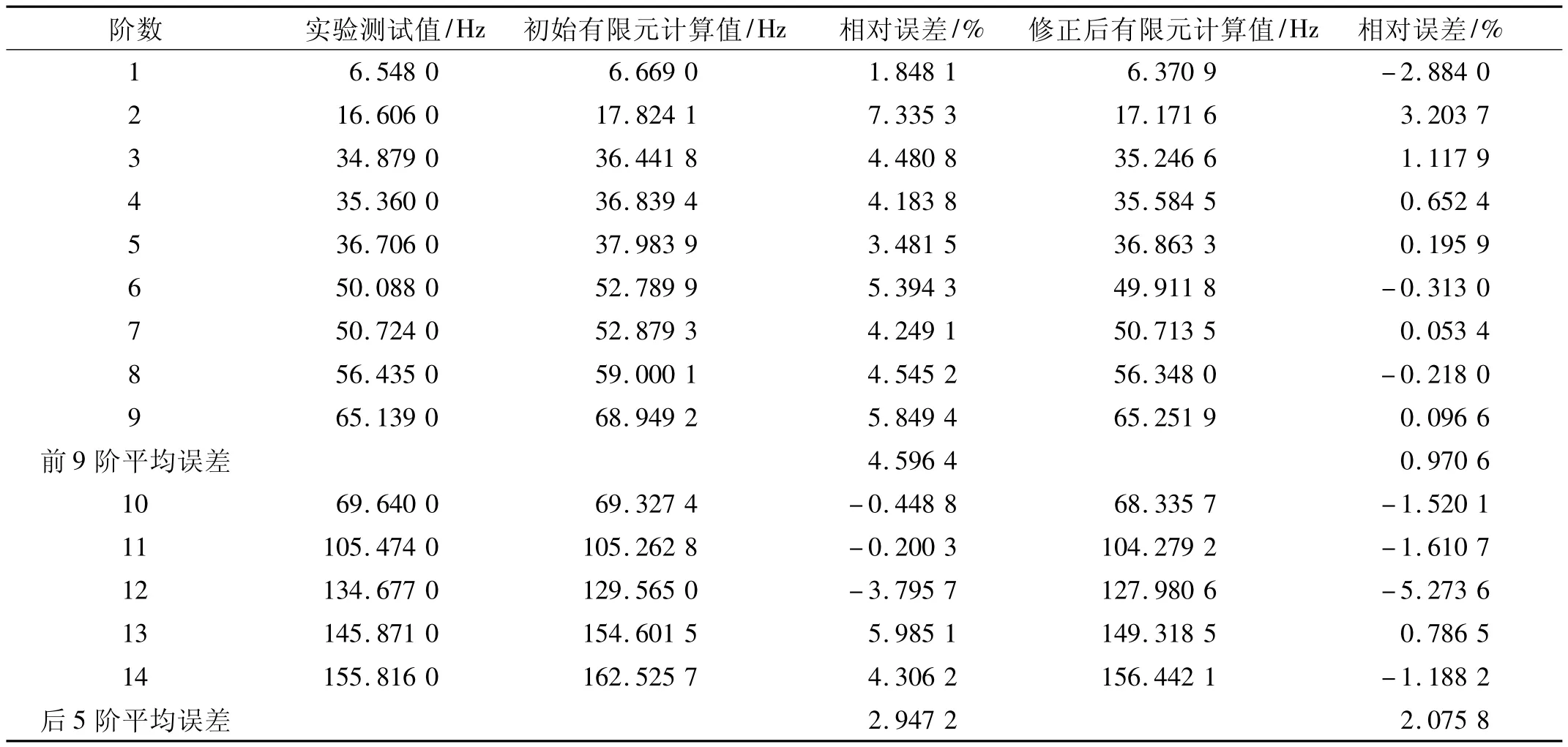
表1 修正前后有限元模型与实验测试频率比较Tab.1 Frequency comparison between finite element model and test data before and after model updating

由于在进行模型修正前只获得了GARTEUR模型实验的频率数据，未能得到模态振型数据，对此采用本文提出的改进方法即利用有限元模型的模态振型代替实验的模态振型，并结合迭代过程不断的进行修正。修正时仅使用实验的前9阶频率数据，10－14阶频率用来检查修正后的模型是否具有预示修正频段外频率的能力。

在模型修正中，为了能够得到满意的模型修正结果，需要合理的选取待修正参数。目前选取待修正参数的方法大多依赖灵敏度分析，该类方法主要选取一些对目标函数灵敏度大的参数进行修正。但是，灵敏度大的参数不一定是存在建模误差的参数［11，12］。因此，基于灵敏度分析的待修正参数选取结果有时并不符合结构真实的情况。利用本文提出的方法对GARTEUR模型进行模型修正，根据经验选取了建模中材料参数不确定的5个连接部位及其附近部位共26个单元作为待修正单元，添加修正后结构总质量为44 kg的物理约束，以单元的杨氏模量及密度作为待修正参数，修正参数总数为52，采用正则化方法对修正方程进行求解，依靠数学方程自动地对存在建模误差的参数进行计算，得到参数的修正量。

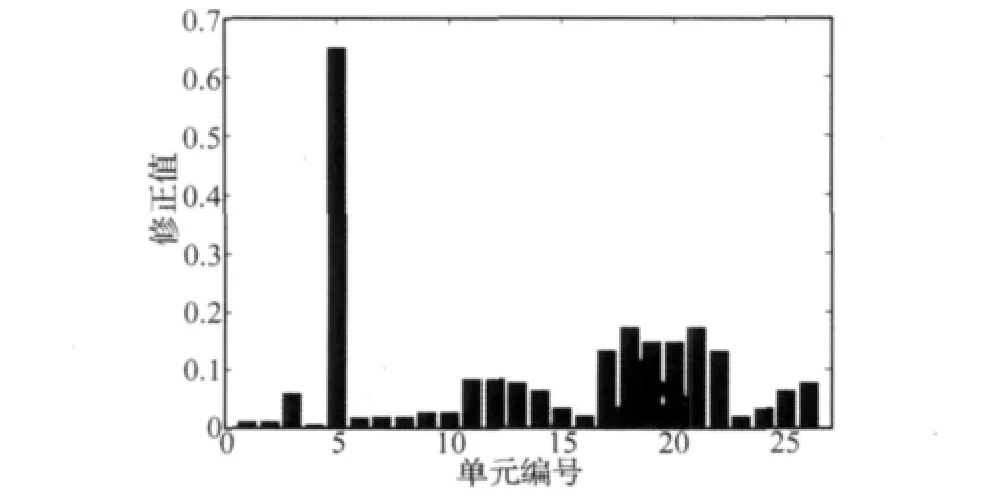
图4 单元杨氏模量修正量Fig.4 Updating results of element Young’s modulus

图4表示参与修正的26个单元的杨氏模量的修正情况。由图4可以看出，单元杨氏模量的修正量与结构真实的状态基本相符，第5单元为机身与机翼之间的连接单元，是整个飞机结构中参数最难以掌握的部位，由于初始建模时杨氏模量取值较小，而真实的连接部位刚度很大，因此该参数获得了较大的修正量。图5表示参与修正的26个单元密度的修正情况。由图5可以看出，单元密度的修正量均未超过12%，符合结构真实的状态。

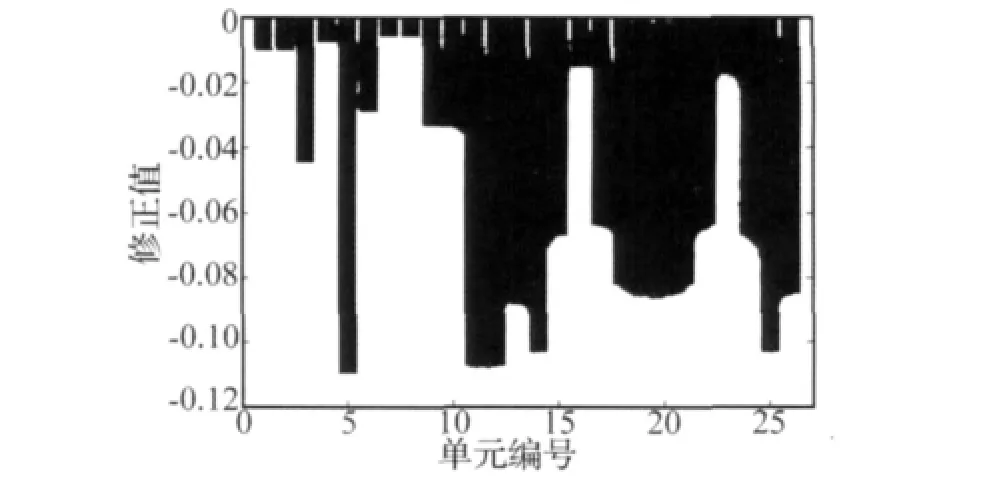
图5 单元密度修正量Fig.5 Updating results of element density

频率修正结果见表1。对初始有限元模型进行修正后，有限元模型的总质量由42.339 kg变为44 kg整，质量的误差由3.78%变为0，由表1可以看到，修正过程中所使用的前9阶频率最大误差由7.3353%变为3.203 7%，平均误差由 4.596 4%变为 0.970 6%，作为校核模型修正效果的后5阶频率最大误差由5.985 1%变为－5.273 6%，平均误差由2.9472%变为2.075 8%。数据表明，修正后的有限元模型不但在所使用频段内误差极大的降低，而且未参与修正的后5阶频率也变得更加的精确。修正后有限元模型的前两阶频率的误差较其它几阶频率大，可能是因为本文并未考虑机翼上粘性阻尼层的原因。

2.2 修正后的模型对修改后GARTEUR模型动力学

特性的预示

为了进一步对初始有限元模型修正结果进行评估，GARTEUR小组对实验模型进行了两种结构修改。对此，在上一节修正后有限元模型的基础上不重新进行修正，而是根据实验修改状况做出相应的调整，得到修改后有限元模型的频率，与修改后GARTEUR模型的实测频率进行比较，这样做的目的是为了防止对初始有限元模型进行修正时只关注修正的数学结果，避免修正结果与结构真实状态不符。好的模型修正结果应该能准确的预示实验模型进行局部修改后的动力学特性。

结构修改1即尾翼修改的修正前后频率比较见表2，修正前频率的平均误差为3.723 6%，最大误差为5.411 1%，修正后频率的平均误差变为1.025 1%，最大误差变为－2.813 4%。结构修改2即机翼修改同样可以得到理想的预示结果，修正前后频率比较见表3，修正前频率的平均误差为3.427 8%，最大误差为6.711 1%，修正后频率的平均误差变为1.260 6%，最大误差变为－4.487 0%。综合上述两种结构修改的比较结果，修正前频率误差超过2%的个数为15个，超过5%的个数为4个，对初始有限元模型进行修正再做相应的修改后频率误差超过2%的个数为4个，未出现频率误差超过5%情况。说明上一节的模型修正的结果能够准确的预示实验模型进行局部修改后的动力学特性，修正后的模型已达到了国际上认可的三级模型修正评价标准。

表2 有限元模型预示频率与测量频率的对比－尾翼修改Tab.2 Comparison between measured frequencies and finite element predictions-tail modification

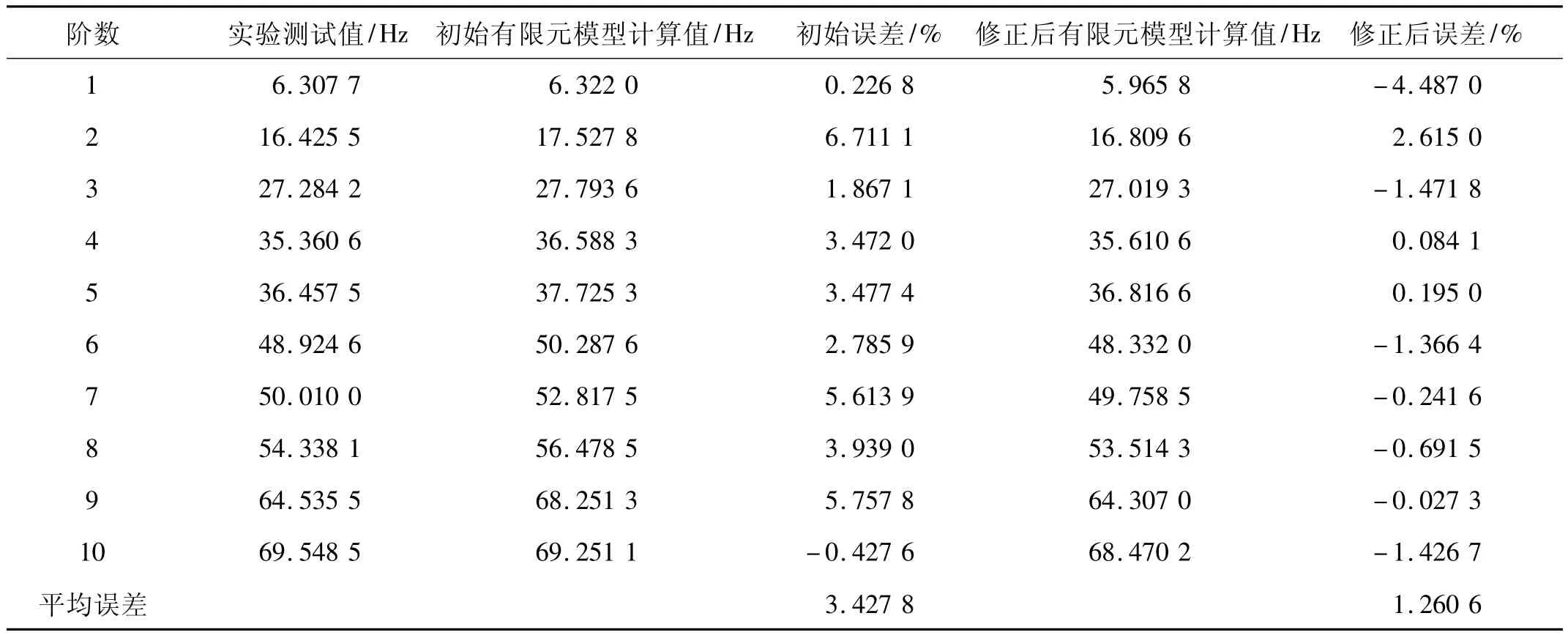
表3 有限元模型预示频率与测量频率的对比－机翼修改Tab.3 Comparison between measured frequencies and finite element predictions-wing modification

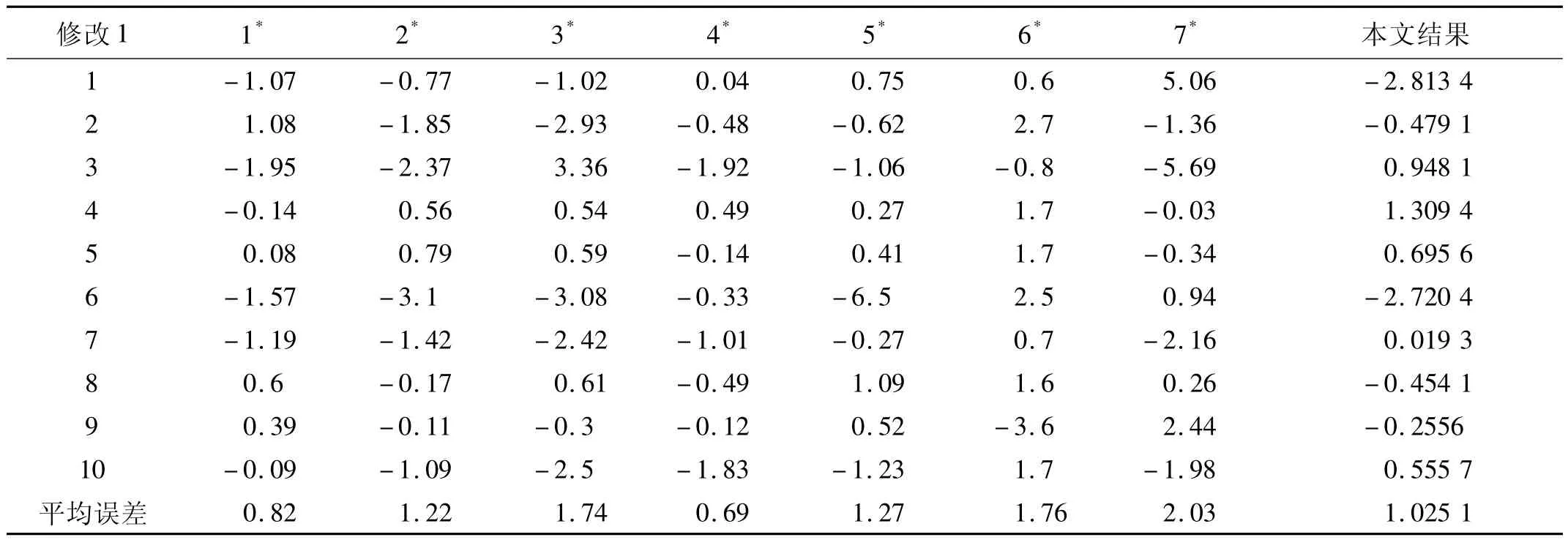
表4 GARTEUR模型修正横向对比－尾翼修改Tab.4 Horizontal comparison of the GARTEUR updating-tail modification

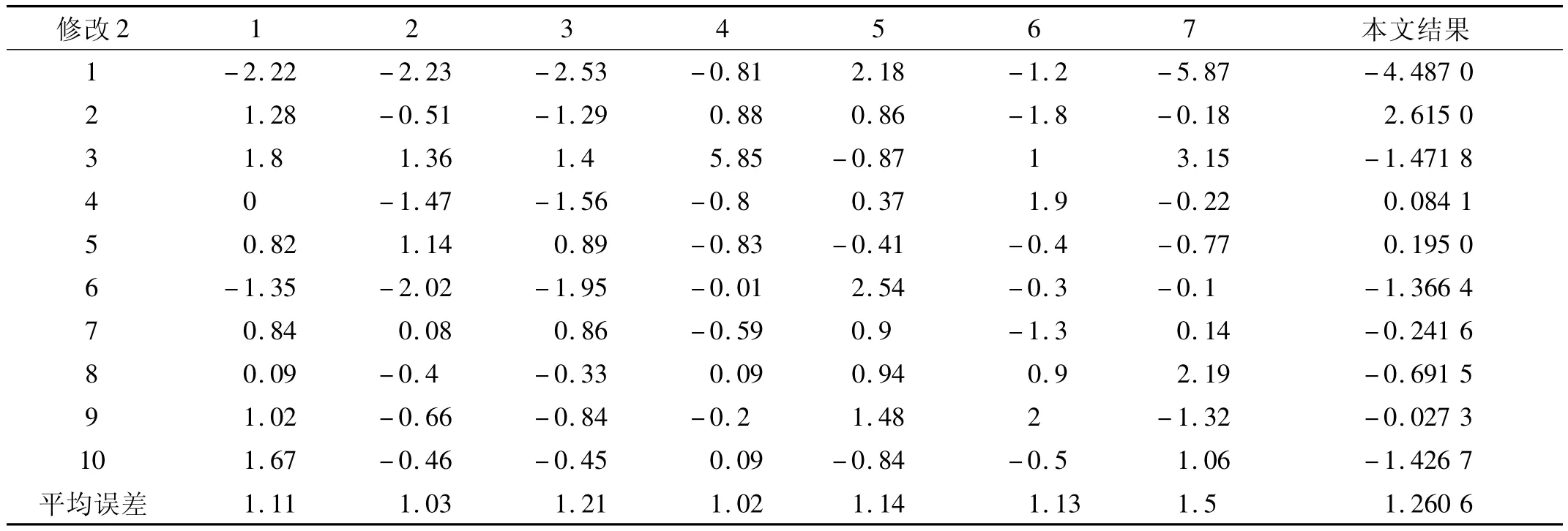
表5 GARTEUR模型修正横向对比－机翼修改Tab.5 Horizontal comparison of the GARTEUR updating-wing modification

表4与表5为本文对GARTEUR模型进行修正的结果与国际上7家同行模型修正结果的横向对比。其中表4为结构修改1的模型修正结果的横向对比，表5为结构修改2的模型修正结果的横向对比。

由于各家单位在所用的修正方法、修正参数、计算方法等方面均有不同，因此模型修正的结果也差异较大，并且没有某家单位的修正结果在各个指标上均处于第一的位置。由表4与表5所示结果可以看到，在最大误差、修正后频率误差超过2%的个数及超过5%的个数和平均误差等4个指标来看，本文的模型修正结果已达到国际同期先进水平。另外，有些模型修正方法需要同时使用实验测量的频率以及振型的数据，但是有些实验对于模态振型的测试比较困难，因此容易造成修正过程中缺少实验数据的问题，本文使用有限元模态振型代替实验模态振型，并通过迭代解决了上述问题，并且依然得到了很好的模型修正效果。

3 结论

本文利用ICMCM法对经典的GARTEUR飞机模型修正问题进行了研究，使用有限元模态代替实验模态并进行迭代，解决了缺少实验模态振型数据的问题。利用Ansys软件建立了GARTEUR飞机结构的模型，并使用ICMCM模型修正方法对其进行修正。修正前后数据比较表明本文的模型修正结果达到了国际上认可的三级模型修正评价标准，最后与国际同行的修正结果进行对比，证明了本文的修正结果达到了国际同期先进水平。以上的研究表明，本文提出的解决缺少实验数据问题的办法是可行的，同时证明了ICMCM法对于复杂的对象具有较高的模型修正能力。

［1］ Mottershead J E，Friswell M I.Model updating in structural dynamics:a survey［J］.Journal of Sound and Vibration，1993，167(2):347－375.

［2］ Friswell M I，Mottershead J E.Finite element model updating in structural dynamics［M］.(Kluwer Academic Publisher，London，1995.

［3］张 纯，宋固全，吴光宇.实测模态和结构模型同步修正的结构损伤识别方法［J］，振动与冲击，2010，29(9):1－4.

［4］袁永新，蒋家尚.一种利用模态测量数据修正刚度矩阵的新方法［J］.振动与冲击，2009，28(11):34－37.

［5］Gravitz S I.An analytical procedure for orthogonalization of measured［J］.MJAS，1958，25(11):1168 －1173.

［6］ Hu S-L J，Li H J，Wang S Q.Cross-model cross-mode method for model updating［J］.Mechanical Systems and Signal Processing，2007，21:1690－1703.

［7］李 剑，洪嘉振，李伟明.模型修正的正交模型－正交模态改进法［J］.动力学与控制，2008，6(1):61－65.

［8］Link M，Friswell M I.Working group 1:Generation of validated structural dynamic models-results of a benchmark study utilising the GARTEUR SM-AG19 test-bed［J］.Mechanical Systems and Signal Processing，2003，17(1):9－20.

［9］Balmes E，Results from the test of a single structure by 12 laboratories in Europe［C］. Proceedingsofthe 15th International Conference on Identification in Engineering，1997:1346－1352.

［10］ Mares C，Mottershead J E，and Friswell M I.Selection and updating of parameters for the GARTEUR SM-AG19 testbed［M］.Proceedings of the 25th International Seminar on Modal Analysis，2000:635 －640.

［11］张令弥.动态有限元模型修正技术及其在航空航天结构中的应用［J］.强度与环境，1994(2):10－17.

［12］ Peter A.Model updating possibilities［M］.Proceedings of the 18th International Modal Analysis Conference，2000，562－570.

Finite element model updating for GARTEUR benchmark model based on ICMCM method

WANG Jin-ming，LI Wei-ming，PENG Ming-feng

(Shanghai Spaceflight Precision Machinery Research Institute，Shanghai 201600，China)

In the model updating process，the experimentally measured frequenices and modal shapes should be used simultaneously when employing improved cross-model cross-mode(ICMCM)method.Here，the modal shapes of the finite element model of a structure were taken as those of its test model and then iterations were used to circumvent the drawback of lacking test modal shapes.Model updating for GARTEUR benchmark model using ICMCM method based on three international criteria and result comparisons with those of other foreign institutions using a traditional model updating method were presented.Results showed the feasibility of the ICMCM method and the advantages of the updated results for GARTEUR benchmark model.

finit element method;model updating;GARTEUR model;iteration

O326;V414.1

A

2011－02－23 修改稿收到日期:2011－03－03

王金明 男，1974年10月生

李伟明 男，博士，1982年01月生